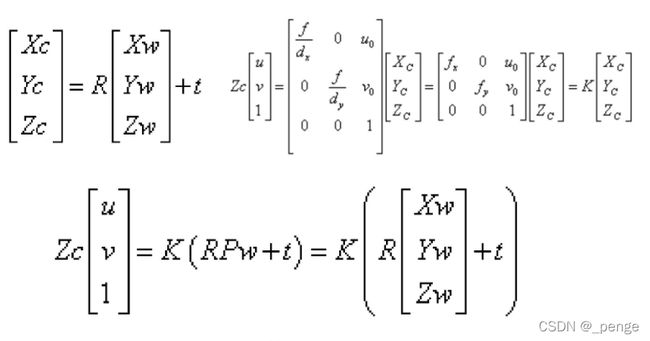计算机视觉基础 相机模型
文章目录
- 相机模型
-
- 世界坐标系到摄像机坐标系
- 摄像机坐标系到图像物理坐标系
- 图像物理坐标系到图像像素坐标系
- 摄像机坐标系到图像像素坐标系
- 世界坐标系到图像像素坐标系
- 相机成像原理
- 镜头畸变
- 透视变换
-
- 定义
- 代码展示
- 应用
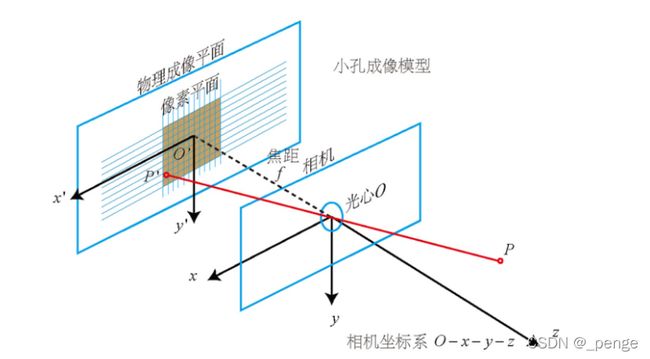
相机模型
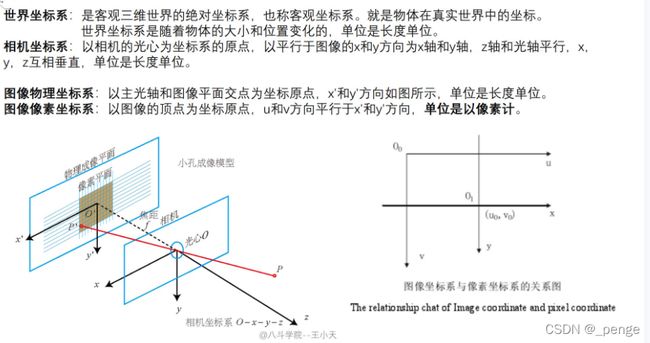
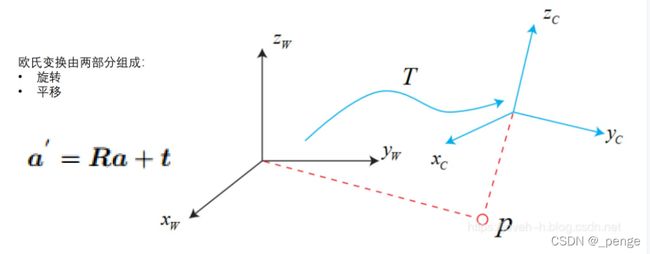
世界坐标系到摄像机坐标系
摄像机坐标系到图像物理坐标系
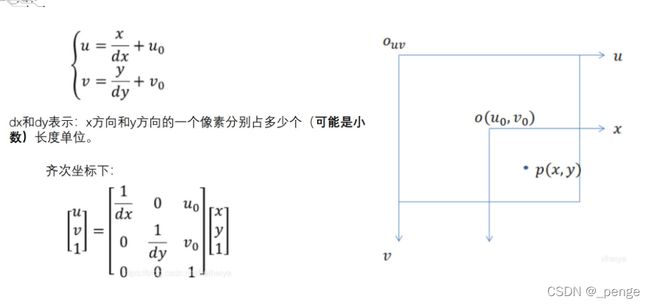
图像物理坐标系到图像像素坐标系
摄像机坐标系到图像像素坐标系
世界坐标系到图像像素坐标系
相机成像原理
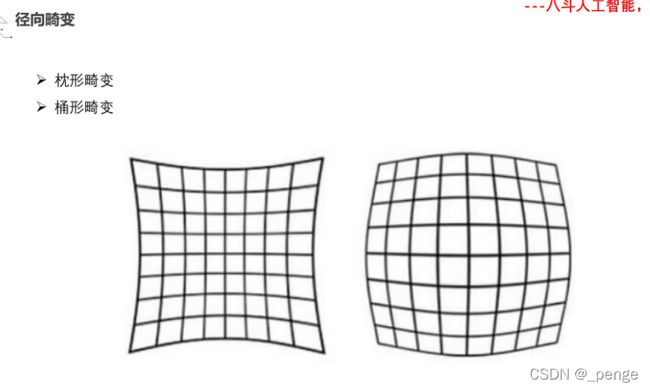
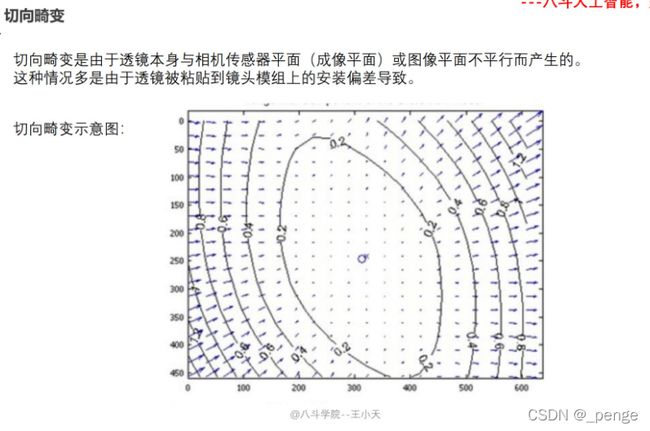
镜头畸变
透视变换
定义
透视变换(Perspective Transformation)是将图片投影到一个新的视平面(Viewing Plane),也称作投影映射(Projective Mapping)
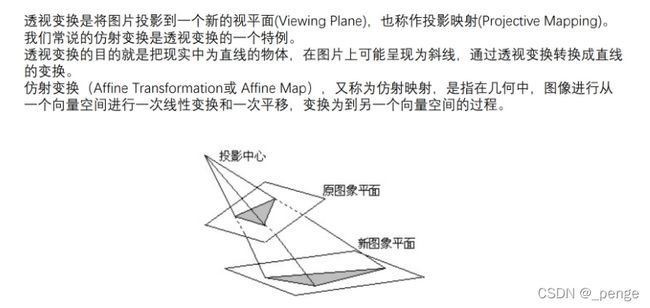


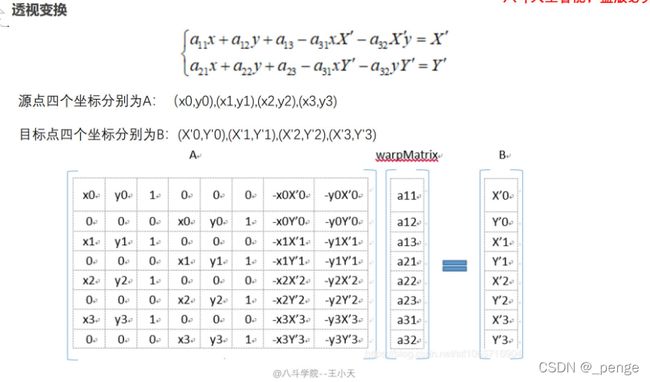
解释:我们的目标是要求出warpMatrix矩阵,所以要找到现图像和将要变化的图像的顶点坐标。因为有8个未知数(3X3的矩阵总共9个参数,我们将A33置为1),所以要找到原坐标和现坐标各4对。带入便可求出warpMatrix矩阵
代码展示
import cv2
import numpy as np
img = cv2.imread('lenna.png')
result3 = img.copy()
'''
注意这里src和dst的输入并不是图像,而是图像对应的顶点坐标。
'''
src = np.float32([[207, 151], [517, 285], [17, 601], [343, 731]])
dst = np.float32([[0, 0], [300, 0], [0, 400], [300, 400]])
print(img.shape)
# 生成透视变换矩阵;进行透视变换
m = cv2.getPerspectiveTransform(src, dst)
print("warpMatrix:")
print(m)
result = cv2.warpPerspective(result3, m, (300, 400))
cv2.imshow("src", img)
cv2.imshow("result", result)
cv2.waitKey(0)
import numpy as np
def WarpPerspectiveMatrix(src, dst):
assert src.shape[0] == dst.shape[0] and src.shape[0] >= 4
nums = src.shape[0]
A = np.zeros((2*nums, 8)) # A*warpMatrix=B
B = np.zeros((2*nums, 1))
for i in range(0, nums):
A_i = src[i,:]
B_i = dst[i,:]
A[2*i, :] = [A_i[0], A_i[1], 1, 0, 0, 0,
-A_i[0]*B_i[0], -A_i[1]*B_i[0]]
B[2*i] = B_i[0]
A[2*i+1, :] = [0, 0, 0, A_i[0], A_i[1], 1,
-A_i[0]*B_i[1], -A_i[1]*B_i[1]]
B[2*i+1] = B_i[1]
A = np.mat(A)
#用A.I求出A的逆矩阵,然后与B相乘,求出warpMatrix
warpMatrix = A.I * B #求出a_11, a_12, a_13, a_21, a_22, a_23, a_31, a_32
#之后为结果的后处理
warpMatrix = np.array(warpMatrix).T[0]
warpMatrix = np.insert(warpMatrix, warpMatrix.shape[0], values=1.0, axis=0) #插入a_33 = 1
warpMatrix = warpMatrix.reshape((3, 3))
return warpMatrix
if __name__ == '__main__':
print('warpMatrix')
src = [[10.0, 457.0], [395.0, 291.0], [624.0, 291.0], [1000.0, 457.0]]
src = np.array(src)
dst = [[46.0, 920.0], [46.0, 100.0], [600.0, 100.0], [600.0, 920.0]]
dst = np.array(dst)
warpMatrix = WarpPerspectiveMatrix(src, dst)
print(warpMatrix)