CV学习笔记【2】：卷积与Conv2

---

前言

本文基于李宏毅的机器学习网课和csdn以及知乎上的有关资料，整理了关于卷积的部分知识。

---

1. 卷积

1.1. 问题引入

使用全联接网络处理一张$100\times 100$的RGB图像时，网络会接收长度为$3\times 100\times 100$的特征向量。假设第一层的神经元个数为1000，第一层的权重就有$3\times 10^7$，这时候需要我们去增加模型的弹性以更好的拟合数据，但参数越多，越容易出现过拟合的情况。

1.2. 影像辨识的问题分析

• 神经网络只需要去检测图片里面有没有一些特别重要的pattern，这些pattern可以唯一确定一个图片的内容
  • 与人分别一个物体是什么的原理是类似的
  • 并不需要每一个神经元都去观测一张完整的图片，只需要把图片的一小部分当作输入，就可以监测到非常重要的pattern
• 同样的特征出现在图片的不同区域
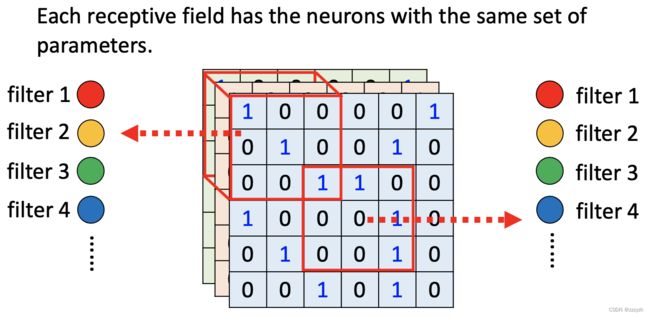
  • 如果每个关注范围都有一个侦测重复特征的neuron，参数量会十分多
  • 不同receptive filed的neuron共享参数

1.3. 简化

1. 感受野（receptive filed）
   The receptive field is defined as the size of the region in the input that produces the feature.
   每一个neuron只需要关注自己的receptive filed即可
   
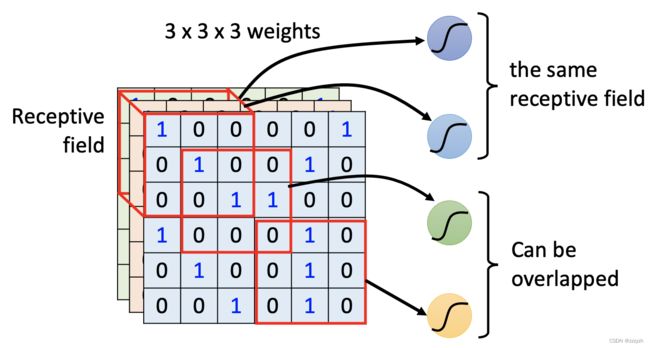
   不同的neurons可以关注同一个receptive filed；不同neurons关注的receptive filed之间也可以有重叠的部分
   

• 设计一个receptive filed
  • receptive filed的大小可以不一样，有的特征可能需要$3\times 3$，有的可能需要$11\times 11$
  • receptive filed可以只考虑图片的一个通道
  • receptive filed也可以是长方形
• Typical setting
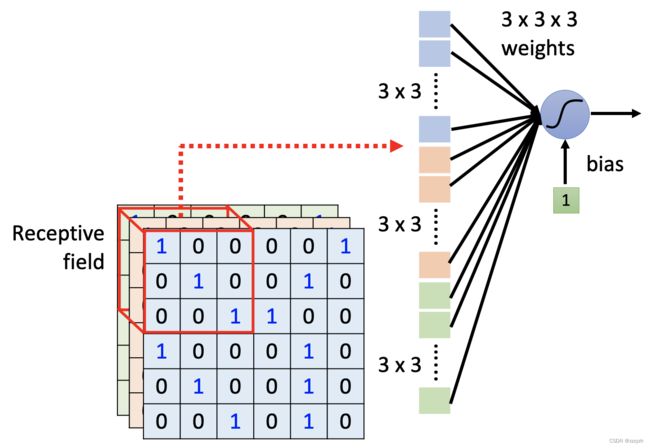
  • 考虑全部的通道
  • 所以感受野的大小往往只需要定义他的长跟宽，即kernel_size
  • 一个receptive filed往往有一组neurons去关注
  • 通过移动原始的receptive filed去获取新的receptive filed，这个移动的长度叫作stride（步长），这个长度通常不会太大，使得receptive filed直接有重叠的部分，以保证检测到位于两个receptive filed之间的特征
  • 在移动receptive filed的过程中，可能会导致新的receptive filed有一部分没有对应的图像（overlap），这个时候需要通过padding去补值
  • receptive filed除了水平移动，还可以上下移动，直到整张图片都被receptive filed覆盖
    

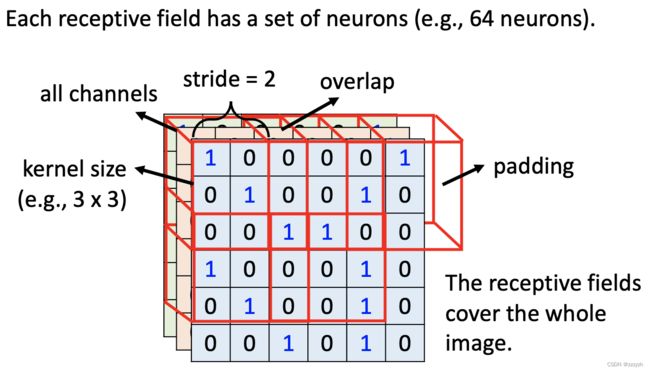
2. 共享参数（parameter sharing）
   参数共享是指在同一个模型的不同模块中使用相同的参数，它是卷积运算的固有属性。全连接网络中，计算每层的输出时，权值参数矩阵中的每个元素只作用于某个输入元素一次；而在卷积神经网络中，卷积核中的每一个元素将作用于每一次局部输入的特定位置上。根据参数共享的思想，我们只需要学习一组参数集合，而不需要针对每个位置的每个参数都进行优化，从而大大降低了模型的存储需求。
   参数共享的物理意义是使得卷积层具有平移等变性。
   
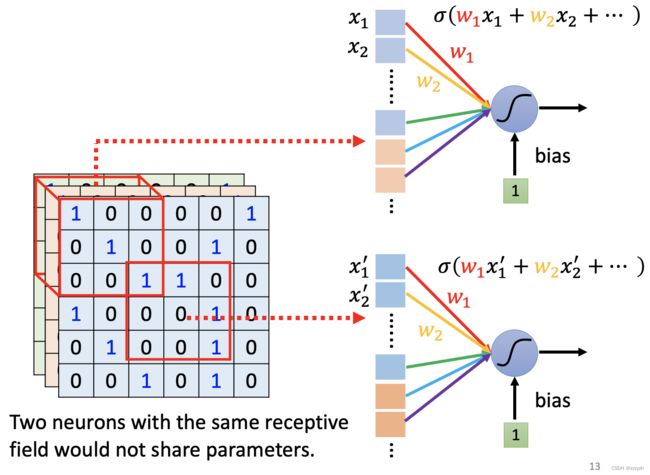
   注意，这里仅权重一致，但是输入不一致，所以输出的结果会跟输入有关，并不会导致输出永远相同

• Typical setting
  • 使用filter
    

1.4. 卷积层（Convolutional Layer）

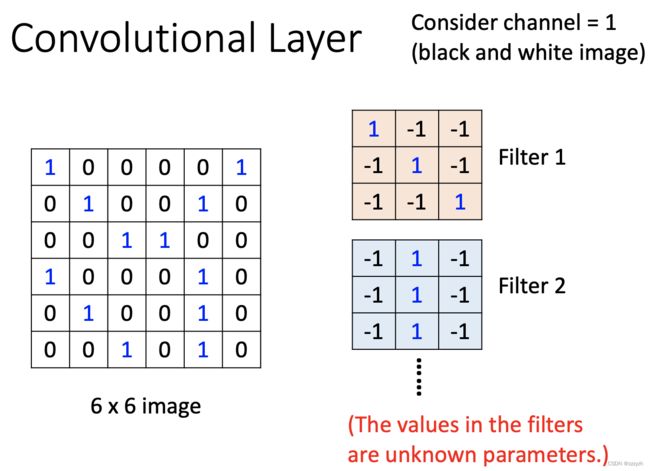
1.4.1. 单通道输入，单卷积核（filter）

• filter 1以步长1扫过该照片，与每一个receptive filed做内积
  
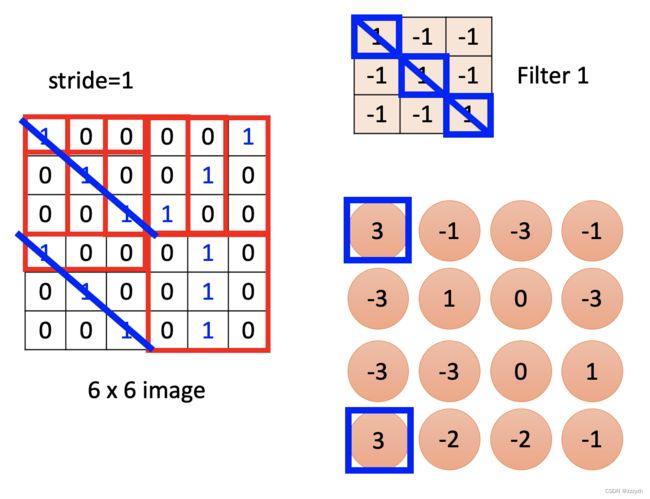
  观察可知，filter 1与receptive filed对角线元素相同的情况代表特征的出现（乘积最大的情况）
• filter 2重复上述的过程
  
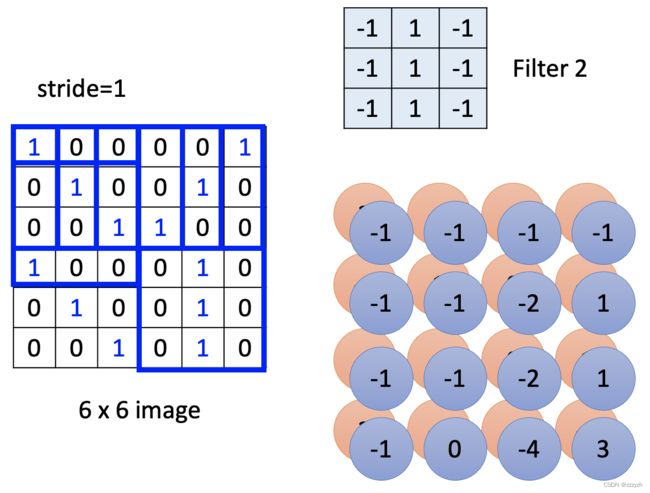
  观察可知，filter 2与receptive filed中间一列元素相同的情况代表特征的出现（乘积最大的情况）
• 当所有的filter扫过一张图片的时候，可以得到一张新的图片，即feature map，此时图片的channel即filter的个数
• 同样可知，filter的通道数量即所需要处理的图片的通道数量，因为例子处理的是黑白照片（通道数为1），所以filter的通道数仅为1；若处理RGB图像，那么对应的filter的通道数也为3

通过两次卷积后的图像我们也可以发现一个小的卷积核是如何处理一个大的pattern的

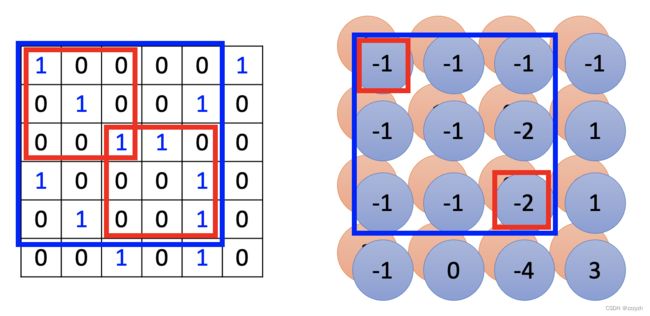
此时如果我们使用kernel_size=3的filter扫过第一次卷积后产生的图像，我们会发现这个时候扫过的大小为3的receptive filed，其实相当于原始图片大小为5的receptive filed。
所以只要network够深，较小的kernel_size也能监测到足够大的pattern

1.4.2. 多通道输入，单卷积核（filter）

每个通道都有一个卷积核，即计算过程就是将单通道输入的过程在输入的三个通道上进行重复
输出的结果是所有通道卷积结果在对应位置上的和（输出结果为一层），新产生的图片的通道数由卷积核的个数决定，与原图片的通道数无关。

1.4.3. 参数共享与卷积核

参数共享就是卷积核

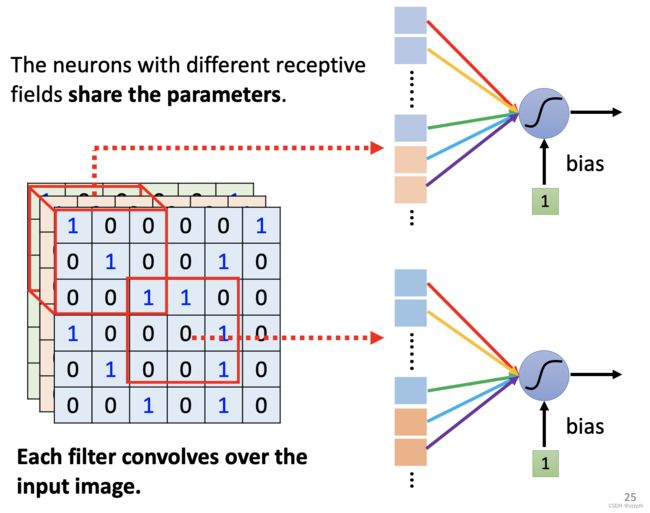
而filter扫过一张图片的过程就是卷积

池化（Pooling）

Subsampling the pixels will not change the object

在通过卷积层获得特征(feature map) 之后，下一步要做的就是利用这些特征进行整合、分类。理论上来讲,所有经过卷积提取得到的特征都可以作为分类器的输入（比如softmax分类器），但这样做会面临着巨大的计算量。
此时我们就会采用池化层将得到的特征（feature map）进行降维。假如我们得到一个局部特征，他是一个图像的一个局部放大图，分辨率很大，那么我们就可以将一些像素点周围的像素点（特征值）近似看待，将平面内某一位置及其相邻位置的特征值进行统计，并将汇总后的结果作为这一位置在该平面的值。

使用池化函数来进一步对卷积操作得到的特征映射结果进行处理。池化会将平面内某未知及其相邻位置的特征值进行统计汇总。使用池化不会造成数据矩阵深度的改变，只会在高度和宽带上降低，达到降维的目的。

• Max Pooling
  最大池化会计算该位置及其相邻矩阵区域内的最大值，并将这个最大值作为该位置的值
  
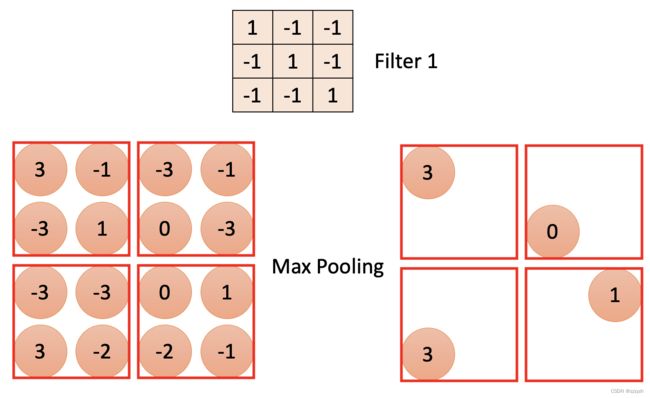
• Mean Pooling
  平均池化会计算该位置及其相邻矩阵区域内的平均值，并将这个值作为该位置的值。

在实际应用上，往往是卷积跟池化交替使用

---

2. nn.Conv2d()

2.1. 参数介绍

import torch
import torch.nn as nn
torch.nn.Conv2d(in_channels=0,
                out_channels=0,
                kernel_size=0,
                stride=1,
                padding=0,
                padding_mode='zeros',
                dilation=1,
                groups=1,
                bias=True)

• in_channels
  参数代表输入特征矩阵的通道数
• out_channels
  参数代表卷积核的个数，输出的通道数即使用的卷积核的个数
• kernel_size
  参数代表卷积核的尺寸
  • int类型：表示一个正方形的卷积核，卷积核的宽即输入的int值
  • tuple类型：可以设置期望的卷积核的形状，(height, weight)
• stride
  参数代表卷积核的步距,默认为1
  • int类型：在水平与竖直方向上具有相同的步长，通常不大于2
  • tuple类型：分别设置水平和竖直方向上的步长，(x, y)

2.2. padding & padding_mode

2.2.1. 使用参数进行填充

• padding
  参数代表在输入特征矩阵四周补值的情况，默认为0
  • int类型：在上下左右各补对应的输入的值的列的像素
  • tuple类型：分别设置上下和左右方向上的补充的像素的列，(x, y)
• padding_mode
  补值的类型，默认为’zeros’
  • ‘zeros’：常量填充
  • ‘reflect’：镜像填充，即以矩阵中的某个行或列为轴，中心对称的padding到最外围。
  • ‘replicate’：重复填充，即直接使用边缘的像素值来填充
  • ‘circular’：循环填充，即从上到下进行无限的重复延伸

2.2.2. 调用函数进行填充

x = torch.Tensor([[1, 2], [3, 4]])

# 零填充
pad = nn.ZeroPad2d(padding=(1, 1, 1, 1))
pad(x)

x = torch.Tensor([[1, 2], [3, 4]])

# 常数填充
pad = nn.ConstantPad2d(padding=(1, 1, 1, 1), value=5)
pad(x)

x = torch.arange(9, dtype=torch.float).reshape(1, 1, 3, 3)

# 镜像填充
pad = nn.ReflectionPad2d(2)
pad(x)

x = torch.arange(9, dtype=torch.float).reshape(1, 1, 3, 3)

# 重复填充
pad = nn.ReplicationPad2d(2)
pad(x)

2.3. dilation

dilation
参数代表kernel内的点（卷积核点）的间距，默认为1

即每个点之间有空隙的过滤器，示意图如下：

空洞卷积主要作用：不丢失分辨率的情况下扩大感受野；调整扩张率获得多尺度信息。进而对对检测大物体有比较好的效果。

2.4. group

group
参数代表filter的组数，默认为1

假设有一个3×3大小的卷积层，其输入通道为16、输出通道为32。具体为，32个3×3大小的卷积核会遍历16个通道中的每个数据，从而产生16×32=512个特征图谱。进而通过叠加每个输入通道对应的特征图谱后融合得到1个特征图谱。最后可得到所需的32个输出通道。

针对这个例子应用深度可分离卷积，用1个3×3大小的卷积核遍历16通道的数据，得到了16个特征图谱。在融合操作之前，接着用32个1×1大小的卷积核遍历这16个特征图谱，进行相加融合。这个过程使用了16×3×3+16×32×1×1=656个参数，远少于上面的16×32×3×3=4608个参数。

---

总结

卷积作为计算机视觉的重要知识
这里仅作整理与一些浅层次内容的探讨