OpenCV笔记整理【霍夫变换】
1. 直线检测
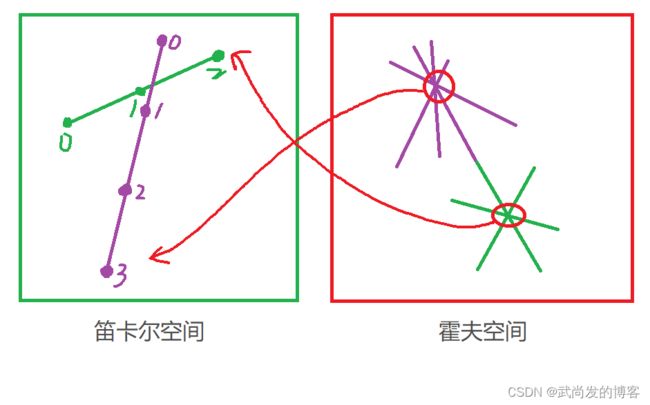
霍夫变换是通过霍夫坐标系的直线与笛卡尔坐标系的点之间的 “映射” 关系来判断图像中的点是否构成直线。
上图中:笛卡尔空间中一条线(y=kx+b),k表示线段的斜率、b表示垂直线段方向的位置。映射到霍夫空间中就是一个点(k,b)。其中,xy是已知的常量,kb是变量。
总结:
-
在笛卡尔空间中多个点如果处在同一条直线上,那么映射到霍夫空间中,多条边会汇聚并穿过同一个交点。
-
在霍夫空间中,经过一个点的直线越多,说明在笛卡尔空间中映射的直线是由越多的点构成的。
所以霍夫变化选择直线的思路就是,选择尽可能多的直线交汇的点。
lines = cv2.HoughLinesP( img, rho, theta, threshold, minLineLength, maxLineGap )
- lines::线段数组 [[x1,y1,x2,y2]…]。
- img::原图。
- rho:半径步长,像素单位。
- theta:搜索角度(Π/180表示检测所有的角度)。
- threshold:阈值,值越小检测的直线就越多。
- minLineLength:最小长度。
- maxLineGap :线段之间的最小距离。
上代码:
import cv2
import numpy as np
img = cv2.imread("pen.jpg") # 读取原图
o = img.copy() # 复制原图
o = cv2.medianBlur(o, 5) # 使用中值滤波进行降噪
gray = cv2.cvtColor(o, cv2.COLOR_BGR2GRAY) # 从彩色图像变成单通道灰度图像
binary = cv2.Canny(o, 50, 150) # 绘制边缘图像
# 检测直线:精度为1,全角度,阈值为15,线段最短100,最小间隔为18
lines = cv2.HoughLinesP(binary, 1, np.pi / 180, 15, minLineLength=100, maxLineGap=18)
for line in lines: # 遍历所有直线
x1, y1, x2, y2 = line[0] # 读取直线两个端点的坐标
cv2.line(img, (x1, y1), (x2, y2), (0, 0, 255), 2) # 在原始图像上绘制直线
cv2.imshow("canny", binary) # 显示二值化边缘图案
cv2.imshow("img", img) # 显示绘制结果
cv2.waitKey() # 按下任何键盘按键后
cv2.destroyAllWindows() # 释放所有窗体
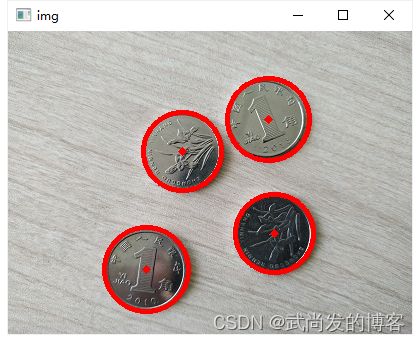
2. 霍夫圆环检测
找圆的策略是: 1. 找出可能存在圆的位置(圆心坐标)。2. 根据第一轮的结果筛选出半径大小。
circles = cv2.HoughCircles(img, method, dp, minDist, param1, param2, minRadius, maxRadius)
- circles:圆的数组 [[x1,y1,r1]…]
- img:原图。
- method:固定使用 cv2.HOUGH_GRADIENT 作为参数。
- dp:分割比率(原图分辨率与圆心累加器的比值,1表示相等,2表示占原图的二分之一)
- minDist:圆心与圆心之间的最小距离。
- param1:Canny检测的边缘的最大阈值(越小越敏感)。
- param2:投票数,默认100(该值越小找到的圆越多)。
- minRadius:限制圆半径的最小值,默认0不做限制。
- maxRadius:限制圆半径的最大值,默认0不做限制。
上代码:
import cv2
import numpy as np
img = cv2.imread("coin.jpg") # 读取原图
o = img.copy() # 复制原图
o = cv2.medianBlur(o, 5) # 使用中值滤波进行降噪
gray = cv2.cvtColor(o, cv2.COLOR_BGR2GRAY) # 从彩色图像变成单通道灰度图像
# 检测圆环,圆心最小间距为80,Canny最大阈值为90,投票数超过25。最小半径为10,最大半径为50
circles = cv2.HoughCircles(gray, cv2.HOUGH_GRADIENT, 1, 90, param1=90, param2=25, minRadius=10, maxRadius=50)
circles = np.uint(np.around(circles)) # 将数组元素四舍五入成整数
for c in circles[0]: # 遍历圆环结果
x, y, r = c # 圆心横坐标、纵坐标和圆半径
cv2.circle(img, (x, y), r, (0, 0, 255), 3) # 绘制圆环
cv2.circle(img, (x, y), 2, (0, 0, 255), 3) # 绘制圆心
cv2.imshow("img", img) # 显示绘制结果
cv2.waitKey() # 按下任何键盘按键后
cv2.destroyAllWindows() # 释放所有窗体