【南瓜书ML】(task1)绪论+模型评估与选择

学习总结

• 学习南瓜书，先看西瓜书本—第1章和第2章主要是讲一些基本概念和术语，可以先跳过以下知识点，等后面部分学完后再来回顾：
  第1章：【1.4-归纳偏好】可以跳过
  第2章：【2.3.3-ROC与AUC】及其以后的都可以跳过
• 高阶指标包括 P-R 曲线，ROC 曲线和平均精度均值。P-R 曲线的横坐标是召回率，纵坐标是精确率；ROC 曲线的横坐标是假阳性率，纵坐标是真阳性率。平均精度均值 mAP是对每个用户的精确率均值的再次平均。

一、机器学习导言

1.1 基本术语和符号表

（1）基本术语

• 学习任务分为两大类：监督学习、无监督学习
• 独立同分布：假设样本空间中，全体样本服从一个未知“分布”，获得的每个样本都是独立地从这个分布上采样获得
• 两大任务：
  • 分类：预测值为离散值的问题
  • 回归：预测值为连续值的问题

其他概念：
归纳、演绎、概念学习、假设空间、版本空间；
归纳偏好（偏好）、奥卡姆剃刀。

（2）符号表（书中常用）

• $x$-一标量
• $\mathbf{x}-$-向量
• $\mathbf{x}$ 一一变量集
• A 一一矩阵
• I-一单位阵
• $\mathcal{X}$ 一一样本空间或状态空间
• D一概率分布
• $D$ —一数据样本（数据集）
• H一一假设空间
• H一一假设集
• L一一学习算法
• $(\cdot ,\cdot ,\cdot )$ 一一行向量
• $(\cdot ;\cdot \cdot )$ 一一列向量
• $(\cdot {)}^{\top }$ 一一向量或矩阵转置
• $\{\cdots \}$ 一一集合
• $|\{\cdots \}|$ 一一集合 $\{\cdots \}$ 中元素的个数
• $\Vert \cdot {\Vert }_p--L_p$ 范数, p缺省时为 $L_2$ 范数
• $P(\cdot ),P(\cdot \mid \cdot )$ 一一概率质量函数, 条件概率质量函数
• $p(\cdot ),p(\cdot \mid \cdot )$ 一一概率密度函数, 条件概率密度函数
• ${\mathbb{E}}_{\sim \sim \mathcal{D}}[f(\cdot )]$ 一一函数 $f(\cdot )$ 对.在分布 $\mathcal{D}$ 下的数学期望；意义明确时将省略 $\mathcal{D}$ 和（或）.
• $\sup (\cdot )$ 一一上确界
• $\mathbb{I}(\cdot )$ 一一指示函数, 在.为真和假时分别取值为 1,0
• $\mathrm{sign}(\cdot )\text{ 一一符号函数, 在 }:<0,=0,>0\text{ 时分别取值为 }-1,0,1$

对上面的几个解释：

• 空间可以简单的理解为集合，假设空间是一个超集（全集）
• 全集的一部分被称为假设集，可以认为假设集是假设空间的一个子集

逗号分割：行向量
分号分割：列向量
指示函数：把逻辑空间映射成{0,1}进而参与运算

1.2 经验误差与过拟合

• 错误率：在m个样本中有个a个样本分类错误，错误率为E=a/m
• 误差：学习器的prediction和样本的真实label之间的差距
• 训练误差or经验误差：学习器在训练集上的误差
• 泛化误差：学习器在新样本上的误差

1.3 公式推导部分

• 假设样本空间 $\mathcal{X}$ 和假设空间 $\mathcal{H}$ 都是离散的. 令 $P\left(h\mid X,{\mathfrak{L}}_a\right)$ 代表算法 ${\mathfrak{L}}_a$ 基于训练数据 $X$ 产生假设 $h$ 的概率
• 令 $f$ 代表我们希望学习的 真实目标函数. ${\mathfrak{L}}_a$ 的 “训练集外误差”, 即 ${\mathfrak{L}}_a$ 在训练集之外的所有样本上的误差为：

$$E_{ote}\left({\mathfrak{L}}_a|X,f\right)=\sum _h\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\mathbb{I}(h(\mathbf{x})\ne f(\mathbf{x}))P\left(h|X,{\mathfrak{L}}_a\right)$$
$\text{ 其中 }\mathbb{I}(\cdot )\text{ 是指示函数, 若. 为真则取值 }1\text{, 否则取值 }0\text{. }$

考虑二分类问题, 且真实目标函数可以是任何函数 $\mathcal{X}\mapsto \{0,1\}$, 函数空间 为 $\{0,1{\}}^{|\mathcal{X}|}$. 对所有可能的 $f$ 按均匀分布对误差求和, 有：
$$\begin{array}{rl}\sum _f{E}_{ote}({\mathfrak{L}}_a|X,f)& =\sum _f\sum _h\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\mathbb{I}(h(\mathbf{x})\ne f(\mathbf{x}))P(h|X,{\mathfrak{L}}_a)\\ & =\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\sum _{h}P(h|X,{\mathfrak{L}}_a)\sum _f\mathbb{I}(h(\mathbf{x})\ne f(\mathbf{x}))\\ & =\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\sum _{h}P(h|X,{\mathfrak{L}}_a)\frac{1}{2}{2}^{|\mathcal{X}|}\\ & =\frac{1}{2}{2}^{|\mathcal{X}|}\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\sum _{h}P(h|X,{\mathfrak{L}}_a)\\ & =2^{|\mathcal{X}|-1}\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\cdot 1\end{array}$$

南瓜书：解析：从第一步到第二步

$$\begin{array}{rl}& \sum _f\sum _h\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\mathbb{I}(h(\mathbf{x})\ne f(\mathbf{x}))P(h|X,{\mathfrak{L}}_a)\\ & =\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\sum _f\sum _h\mathbb{I}(h(\mathbf{x})\ne f(\mathbf{x}))P(h|X,{\mathfrak{L}}_a)\\ & =\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\sum _{h}P(h|X,{\mathfrak{L}}_a)\sum _f\mathbb{I}(h(\mathbf{x})\ne f(\mathbf{x}))\end{array}$$

第 2 步到第 3 步:
首先要知道此时我们对 $f$ 的假设是任何能将样本映射到 0,1 的函数且服从均匀分布, 也就是说不止一个 $f$ 且每个 $f$ 出现的概率相等, 例如样本空间只有两个样本时: $\mathcal{X}=\left\{x_1,x_2\right\},|\mathcal{X}|=2$, 那 么所有的真实目标函数 $f$ 为：
$$\begin{array}{r}{f}_1:f_1({\mathbf{x}}_1)=0,f_1({\mathbf{x}}_2)=0;\\ f_2:f_2({\mathbf{x}}_1)=0,f_2({\mathbf{x}}_2)=1;\\ f_3:f_3({\mathbf{x}}_1)=1,f_3({\mathbf{x}}_2)=0;\\ f_4:f_4({\mathbf{x}}_1)=1,f_4({\mathbf{x}}_2)=1;\end{array}$$
一共 $2^{|x|}=2^2=4$ 个真实目标函数。
所以此时通过算法 ${\mathfrak{L}}_a$ 学习出来的模型 $h(\mathbf{x})$ 对每个样本无论 预测值为 0 还是 1 必然有一半的 $f$ 与之预测值相等, 例如, 现在学出来的模型 $h(x)$ 对 $x_1$ 的预测值 为 1 , 也即 $h\left({\mathbf{x}}_1\right)=1$, 那么有且只有 $f_3$ 和 $f_4$ 与 $h(\mathbf{x})$ 的预测值相等, 也就是有且只有一半的 $f$ 与 它预测值相等, 所以 ${\sum }_f\mathbb{I}(h(x)\ne f(x))=\frac{1}{2}{2}^{|X|}$; 第 3 步一直到最后显然成立。

在这里假设真实的目标函数 $f$ 为 “任何能将样本映射到 0,1 的函数且服从均匀分布”, 但是实际情形并非如此, 通常我们只认为能高度拟合已有样本数据的函数才是真实目标函数：

• 例如, 现在已有的样本 数据为 $\left\{\left(x_1,0\right),\left(x_2,1\right)\right\}$, 那么此时 $f_2$ 才是我们认为的真实目标函数, 由于没有收集到或者压根不存在 $\left\{\left(x_1,0\right),\left(x_2,0\right)\right\},\left\{\left(x_1,1\right),\left(x_2,0\right)\right\},\left\{\left(x_1,1\right),\left(x_2,1\right)\right\}$ 这类样本

所以 $f_1,f_3,f_4$ 都不算是真实目标函数。这也就是西瓜书公式 (1.3) 下面的第 3 段话举的 “骑自行车” 的例子所想表达的内容。

二、模型评估

2.0 几个评估方法

（1）留出法（hold-out）

最简单常用的，将数据集划分为训练集和测试集（2个集合互斥）。

（2）交叉验证法

【交叉验证的工作原理】
如果要对测试误差进行估计，有训练误差修正和交叉验证两种方式。前者是通过训练误差的桥梁的一种间接方式；而交叉验证是对测试误差的直接估计。

【K折交叉验证】
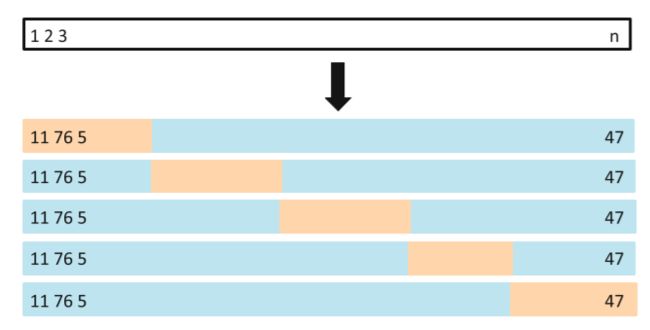
K折交叉验证：我们把训练样本分成K等分，然后用K-1个样本集当做训练集，剩下的一份样本集为验证集去估计由K-1个样本集得到的模型的精度，这个过程重复K次取平均值得到测试误差的一个估计$C{V}_{(K)}=\frac{1}{K}\sum _{i=1}^{K}MS{E}_i$。5折交叉验证如下图：（蓝色的是训练集，橙色的是验证集）

（3）自助法

概念: 给定包含 $m$ 个样本的数据集 $D$, 每次随本, 将其拷贝放入 $D^{\prime }$, 然后再将该样本放回初始数据集 $D$ 中, 使得该 样本在下次采样时仍有可能被采到。重复执行 $m$ 次, 就可以得到了包 含 $m$ 个样本的数据集 $D^{\prime }$ 。可以得知在 $m$ 次采样中, 样本始终不被采到 的概率取极限为:
$$\underset{m\to \infty }{\lim }{\left(1-\frac{1}{m}\right)}^m\to \frac{1}{e}\approx 0.368$$
通过自助采样, 初始样本集D中大约有 $36.8\%$ 的样本没有出 现在 $D^{\prime }$ 中, 于是可以将 $D^{\prime }$ 作为训练集, $D-D^{\prime }$ 作为测试集。

2.1 几个评估指标

混淆矩阵：

（1）精确率（precision，P值）

是针对我们预测结果而言的，它表示的是预测为正的样本中有多少是真正的正样本。那么预测为正就有两种可能了，一种就是把正类预测为正类(TP)，另一种就是把负类预测为正类(FP)，也就是
$$P=\frac{TP}{TP+FP}$$

（2）召回率（Recall，R值）

是针对我们原来的样本而言的，它表示的是样本中的正例有多少被预测正确了。那也有两种可能，一种是把原来的正类预测成正类(TP)，另一种就是把原来的正类预测为负类(FN，F即预测错)：
$$R=\frac{TP}{TP+FN}$$

【小栗子】
有60个正样本，40个负样本，我们要找出所有的正样本，系统查找出50个，其中只有40个是真正的正样本，计算上述各指标。

• TP: 将正类预测为正类数 40
• FN: 将正类预测为负类数 20
• FP: 将负类预测为正类数 10
• TN: 将负类预测为负类数 30

准确率(accuracy) = 预测对的/所有 = (TP+TN)/(TP+FN+FP+TN) = 70%
精确率(precision) = TP/(TP+FP) = 80%
召回率(recall) = TP/(TP+FN) = 2/3

（3）准确率和召回率的权衡

F1值：P和R指标有时候会出现的矛盾的情况，这样就需要综合考虑他们，最常见的方法就是F-Measure，通过计算F值来评价一个指标！

F1-score 的值越高，就证明模型在精确率和召回率的整体表现上越好。
$$\mathrm{F}1=\frac{2\cdot \text{ precision }\cdot \text{ recall }}{\text{ precision }+\text{ recall }}$$

2.2 错误率和精度

错误率：
$$E(f;D)=\frac{1}{m}\sum _{i=1}^{m}I\left(f\left(x_i\right)\ne y_i\right)$$
精度：$$\begin{array}{rl}\mathrm{acc}(f;D)& =\frac{1}{m}\sum _{i=1}^{m}I\left(f\left(x_i\right)=y_i\right)\\ & =1-E(f;D)\end{array}$$

2.3 公式推导部分（还需研究）

（1）AUC公式（公式2.20）

$$\text{AUC}=\frac{1}{2}\sum _{i=1}^{m-1}(x_{i+1}-x_i)\cdot (y_i+y_{i+1})$$
[解析]：在解释$\text{AUC}$公式之前，我们需要先弄清楚$\text{ROC}$曲线的具体绘制过程，下面我们就举个例子，按照西瓜书图2.4下方给出的绘制方法来讲解一下$\text{ROC}$曲线的具体绘制过程。假设我们已经训练得到一个学习器$f(s)$，现在用该学习器来对我们的8个测试样本（4个正例，4个反例，也即$m^{+}=m^{-}=4$）进行预测，假设预测结果为：
$$(s_1,0.77,+),(s_2,0.62,-),(s_3,0.58,+),(s_4,0.47,+),(s_5,0.47,-),(s_6,0.33,-),(s_7,0.23,+),(s_8,0.15,-)$$
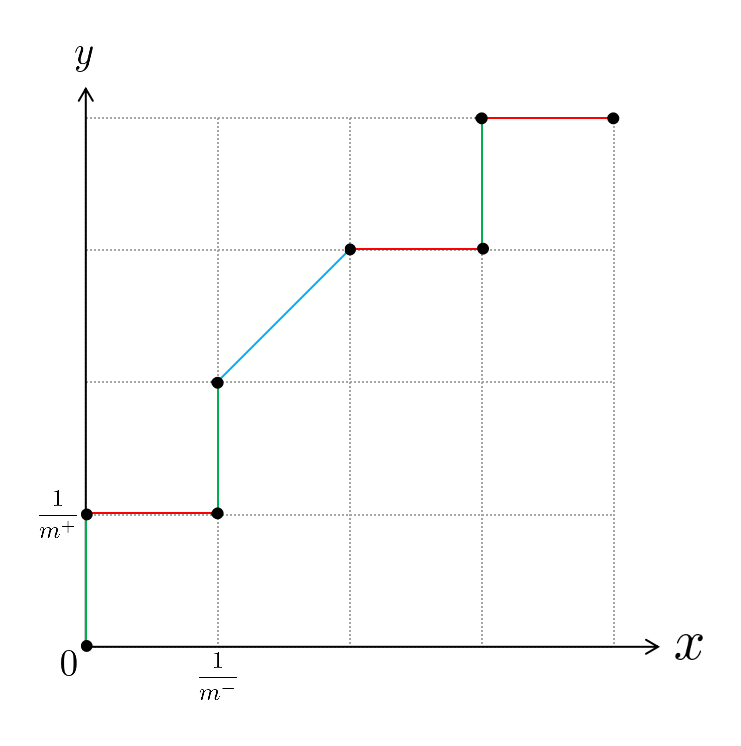
其中，$+$和$-$分别表示为正例和为反例，里面的数字表示学习器$f(s)$预测该样本为正例的概率，例如对于反例$s_2$来说，当前学习器$f(s)$预测它是正例的概率为$0.62$。根据西瓜书上给出的绘制方法可知，首先需要对所有测试样本按照学习器给出的预测结果进行排序（上面给出的预测结果已经按照预测值从大到小排好），接着将分类阈值设为一个不可能取到的最大值，显然这时候所有样本预测为正例的概率都一定小于分类阈值，那么预测为正例的样本个数为0，相应的真正例率和假正例率也都为0，所以此时我们可以在坐标$(0,0)$处打一个点。接下来我们需要把分类阈值从大到小依次设为每个样本的预测值，也就是依次设为$0.77、0.62、0.58、0.47、0.33、0.23、0.15$，然后每次计算真正例率和假正例率，再在相应的坐标上打一个点，最后再将各个点用直线串连起来即可得到$\text{ROC}$曲线。需要注意的是，在统计预测结果时，预测值等于分类阈值的样本也算作预测为正例。例如，当分类阈值为$0.77$时，测试样本$s_1$被预测为正例，由于它的真实标记也是正例，所以此时$s_1$是一个真正例。为了便于绘图，我们将$x$轴（假正例率轴）的“步长”定为$\frac{1}{m^{-}}$，$y$轴（真正例率轴）的“步长”定为$\frac{1}{m^{+}}$，这样的话，根据真正例率和假正例率的定义可知，每次变动分类阈值时，若新增$i$个假正例，那么相应的$x$轴坐标也就增加$\frac{i}{m^{-}}$，同理，若新增$j$个真正例，那么相应的$y$轴坐标也就增加$\frac{j}{m^{+}}$。按照以上讲述的绘制流程，最终我们可以绘制出如下图所示的$\text{ROC}$曲线：

在这里我们为了能在解析公式(2.21)时复用此图所以没有写上具体地数值，转而用其数学符号代替。其中绿色线段表示在分类阈值变动的过程中只新增了真正例，红色线段表示只新增了假正例，蓝色线段表示既新增了真正例也新增了假正例。根据$\text{AUC}$值的定义可知，此时的$\text{AUC}$值其实就是所有红色线段和蓝色线段与$x$轴围成的面积之和。观察上图可知，红色线段与$x$轴围成的图形恒为矩形，蓝色线段与$x$轴围成的图形恒为梯形，但是由于梯形面积公式既能算梯形面积，也能算矩形面积，所以无论是红色线段还是蓝色线段，其与$x$轴围成的面积都能用梯形公式来计算，也即

$$\frac{1}{2}\cdot (x_{i+1}-x_i)\cdot (y_i+y_{i+1})$$
其中$(x_{i+1}-x_i)$表示“高”，$y_i$表示“上底”，$y_{i+1}$表示“下底”。那么
$$\sum _{i=1}^{m-1}\left[\frac{1}{2}\cdot (x_{i+1}-x_i)\cdot (y_i+y_{i+1})\right]$$
表示的便是对所有红色线段和蓝色线段与$x$轴围成的面积进行求和，此即为$\text{AUC}$。

（2）排序中的loss函数定义（公式2.21）

$${\ell }_{rank}=\frac{1}{m^{+}{m}^{-}}\sum _{{\mathbf{x}}^{+}\in D^{+}}\sum _{{\mathbf{x}}^{-}\in D^{-}}\left(\mathbb{I}\left(f({\mathbf{x}}^{+})<f({\mathbf{x}}^{-})\right)+\frac{1}{2}\mathbb{I}\left(f({\mathbf{x}}^{+})=f({\mathbf{x}}^{-})\right)\right)$$
[解析]：按照我们上述对公式(2.20)的解析思路，${\ell }_{rank}$可以看作是所有绿色线段和蓝色线段与$y$轴围成的面积之和，但是公式(2.21)很难一眼看出其面积的具体计算方式，因此我们需要将公式(2.21)进行恒等变形
$$\begin{array}{rl}{\ell }_{rank}& =\frac{1}{m^{+}{m}^{-}}\sum _{{\mathbf{x}}^{+}\in D^{+}}\sum _{{\mathbf{x}}^{-}\in D^{-}}\left(\mathbb{I}\left(f({\mathbf{x}}^{+})<f({\mathbf{x}}^{-})\right)+\frac{1}{2}\mathbb{I}\left(f({\mathbf{x}}^{+})=f({\mathbf{x}}^{-})\right)\right)\\ & =\frac{1}{m^{+}{m}^{-}}\sum _{{\mathbf{x}}^{+}\in D^{+}}\left[\sum _{{\mathbf{x}}^{-}\in D^{-}}\mathbb{I}\left(f({\mathbf{x}}^{+})<f({\mathbf{x}}^{-})\right)+\frac{1}{2}\cdot \sum _{{\mathbf{x}}^{-}\in D^{-}}\mathbb{I}\left(f({\mathbf{x}}^{+})=f({\mathbf{x}}^{-})\right)\right]\\ & =\sum _{{\mathbf{x}}^{+}\in D^{+}}\left[\frac{1}{m^{+}}\cdot \frac{1}{m^{-}}\sum _{{\mathbf{x}}^{-}\in D^{-}}\mathbb{I}\left(f({\mathbf{x}}^{+})<f({\mathbf{x}}^{-})\right)+\frac{1}{2}\cdot \frac{1}{m^{+}}\cdot \frac{1}{m^{-}}\sum _{{\mathbf{x}}^{-}\in D^{-}}\mathbb{I}\left(f({\mathbf{x}}^{+})=f({\mathbf{x}}^{-})\right)\right]\\ & =\sum _{{\mathbf{x}}^{+}\in D^{+}}\frac{1}{2}\cdot \frac{1}{m^{+}}\cdot \left[\frac{2}{m^{-}}\sum _{{\mathbf{x}}^{-}\in D^{-}}\mathbb{I}\left(f({\mathbf{x}}^{+})<f({\mathbf{x}}^{-})\right)+\frac{1}{m^{-}}\sum _{{\mathbf{x}}^{-}\in D^{-}}\mathbb{I}\left(f({\mathbf{x}}^{+})=f({\mathbf{x}}^{-})\right)\right]\end{array}$$
根据公式(2.20)中给出的$\text{ROC}$曲线图可知，在变动分类阈值的过程当中，如果有新增真正例，那么相应地就会增加一条绿色线段或蓝色线段，所以上式中的$\sum _{{\mathbf{x}}^{+}\in D^{+}}$可以看作是在遍历所有绿色和蓝色线段，那么相应地$\sum _{{\mathbf{x}}^{+}\in D^{+}}$后面的那一项便是在求绿色线段或者蓝色线段与$y$轴围成的面积，也即
$$\frac{1}{2}\cdot \frac{1}{m^{+}}\cdot \left[\frac{2}{m^{-}}\sum _{{\mathbf{x}}^{-}\in D^{-}}\mathbb{I}\left(f({\mathbf{x}}^{+})<f({\mathbf{x}}^{-})\right)+\frac{1}{m^{-}}\sum _{{\mathbf{x}}^{-}\in D^{-}}\mathbb{I}\left(f({\mathbf{x}}^{+})=f({\mathbf{x}}^{-})\right)\right]$$
同公式(2.20)中的求解思路一样，不论是绿色线段还是蓝色线段，其与$y$轴围成的图形面积都可以用梯形公式来进行计算，所以上式表示的依旧是一个梯形的面积求解公式。其中$\frac{1}{m^{+}}$即为梯形的“高”，中括号中的那一项便是“上底+下底”，下面我们来分别推导一下“上底”（较短的那个底）和“下底”。由于在绘制$\text{ROC}$曲线的过程中，每新增一个假正例时$x$坐标也就新增一个单位，所以对于“上底”，也就是绿色或者蓝色线段的下端点到$y$轴的距离，它就等于$\frac{1}{m^{-}}$乘以预测值比${\mathbf{x}}^{+}$大的假正例的个数，也即
$$\frac{1}{m^{-}}\sum _{{\mathbf{x}}^{-}\in D^{-}}\mathbb{I}\left(f({\mathbf{x}}^{+})<f({\mathbf{x}}^{-})\right)$$
而对于“下底”，它就等于$\frac{1}{m^{-}}$乘以预测值大于等于${\mathbf{x}}^{+}$的假正例的个数，也即
$$\frac{1}{m^{-}}\left(\sum _{{\mathbf{x}}^{-}\in D^{-}}\mathbb{I}\left(f({\mathbf{x}}^{+})<f({\mathbf{x}}^{-})\right)+\sum _{{\mathbf{x}}^{-}\in D^{-}}\mathbb{I}\left(f({\mathbf{x}}^{+})=f({\mathbf{x}}^{-})\right)\right)$$

（3）假设检验中的置信度（公式2.27）

$$\overline{ϵ}=\min ϵ\text{ s.t. }\sum _{i=ϵ\times m+1}^m\left(\begin{array}{c}m\\ i\end{array}\right){ϵ}_0^i(1-{ϵ}_0{)}^{m-i}<\alpha$$
具体推导过程如下：由西瓜书中的上下文可知，对$ϵ\le {ϵ}_0$进行假设检验，等价于附录①中所述的对$p\le p_0$进行假设检验，所以在西瓜书中求解最大错误率$\overline{ϵ}$等价于在附录①中求解事件最大发生频率$\frac{\overline{C}}{m}$。由附录①可知
$$\overline{C}=\min C\text{ s.t. }\sum _{i=C+1}^m\left(\begin{array}{c}m\\ i\end{array}\right)p_0^i(1-p_0{)}^{m-i}<\alpha$$
所以
$$\frac{\overline{C}}{m}=\min \frac{C}{m}\text{ s.t. }\sum _{i=C+1}^m\left(\begin{array}{c}m\\ i\end{array}\right)p_0^i(1-p_0{)}^{m-i}<\alpha$$
将上式中的$\frac{\overline{C}}{m},\frac{C}{m},p_0$等价替换为$\overline{ϵ},ϵ,{ϵ}_0$可得
$$\overline{ϵ}=\min ϵ\text{ s.t. }\sum _{i=ϵ\times m+1}^m\left(\begin{array}{c}m\\ i\end{array}\right){ϵ}_0^i(1-{ϵ}_0{)}^{m-i}<\alpha$$

（4）对期望泛化误差进行分解（公式2.41）

$$\begin{array}{rl}E(f;D)=& {\mathbb{E}}_D\left[{\left(f(\mathbf{x};D)-y_D\right)}^2\right]\\ =& {\mathbb{E}}_D\left[{\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})+\bar{f}(\mathbf{x})-y_D\right)}^2\right]\\ =& {\mathbb{E}}_D\left[{\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)}^2\right]+{\mathbb{E}}_D\left[{\left(\bar{f}(\mathbf{x})-y_D\right)}^2\right]\\ & +{\mathbb{E}}_D\left[+2\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)\left(\bar{f}(\mathbf{x})-y_D\right)\right]\\ =& {\mathbb{E}}_D\left[{\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)}^2\right]+{\mathbb{E}}_D\left[{\left(\bar{f}(\mathbf{x})-y_D\right)}^2\right]\\ =& {\mathbb{E}}_D\left[{\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)}^2\right]+{\mathbb{E}}_D\left[{\left(\bar{f}(\mathbf{x})-y+y-y_D\right)}^2\right]\\ =& {\mathbb{E}}_D\left[{\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)}^2\right]+{\mathbb{E}}_D\left[{\left(\bar{f}(\mathbf{x})-y\right)}^2\right]+{\mathbb{E}}_D\left[{\left(y-y_D\right)}^2\right]\\ & +2{\mathbb{E}}_D\left[\left(\bar{f}(\mathbf{x})-y\right)\left(y-y_D\right)\right]\\ =& {\mathbb{E}}_D\left[{\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)}^2\right]+{\left(\bar{f}(\mathbf{x})-y\right)}^2+{\mathbb{E}}_D\left[{\left(y_D-y\right)}^2\right]\end{array}$$

[解析]：

• 第1-2步：减一个$\bar{f}(\mathbf{x})$再加一个$\bar{f}(\mathbf{x})$，属于简单的恒等变形；
• 第2-3步：首先将中括号里面的式子展开
  $${\mathbb{E}}_D\left[{\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)}^2+{\left(\bar{f}(\mathbf{x})-y_D\right)}^2+2\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)\left(\bar{f}(\mathbf{x})-y_D\right)\right]$$
  然后根据期望的运算性质：$\mathbb{E}[X+Y]=\mathbb{E}[X]+\mathbb{E}[Y]$可将上式化为
  $${\mathbb{E}}_D\left[{\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)}^2\right]+{\mathbb{E}}_D\left[{\left(\bar{f}(\mathbf{x})-y_D\right)}^2\right]+{\mathbb{E}}_D\left[2\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)\left(\bar{f}(\mathbf{x})-y_D\right)\right]$$
• 第3-4步：再次利用期望的运算性质将第3步得到的式子的最后一项展开
  $${\mathbb{E}}_D\left[2\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)\left(\bar{f}(\mathbf{x})-y_D\right)\right]={\mathbb{E}}_D\left[2\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)\cdot \bar{f}(\mathbf{x})\right]-{\mathbb{E}}_D\left[2\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)\cdot y_D\right]$$
  • 首先计算展开后得到的第一项
    $${\mathbb{E}}_D\left[2\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)\cdot \bar{f}(\mathbf{x})\right]={\mathbb{E}}_D\left[2f(\mathbf{x};D)\cdot \bar{f}(\mathbf{x})-2\bar{f}(\mathbf{x})\cdot \bar{f}(\mathbf{x})\right]$$
    由于$\bar{f}(\mathbf{x})$是常量，所以由期望的运算性质：$\mathbb{E}[AX+B]=A\mathbb{E}[X]+B$（其中$A,B$均为常量）可得
    $${\mathbb{E}}_D\left[2\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)\cdot \bar{f}(\mathbf{x})\right]=2\bar{f}(\mathbf{x})\cdot {\mathbb{E}}_D\left[f(\mathbf{x};D)\right]-2\bar{f}(\mathbf{x})\cdot \bar{f}(\mathbf{x})$$
    由公式（2.37）可知：${\mathbb{E}}_D\left[f(\mathbf{x};D)\right]=\bar{f}(\mathbf{x})$，所以
    $${\mathbb{E}}_D\left[2\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)\cdot \bar{f}(\mathbf{x})\right]=2\bar{f}(\mathbf{x})\cdot \bar{f}(\mathbf{x})-2\bar{f}(\mathbf{x})\cdot \bar{f}(\mathbf{x})=0$$
  • 接着计算展开后得到的第二项
    $${\mathbb{E}}_D\left[2\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)\cdot y_D\right]=2{\mathbb{E}}_D\left[f(\mathbf{x};D)\cdot y_D\right]-2\bar{f}(\mathbf{x})\cdot {\mathbb{E}}_D\left[y_D\right]$$
    由于噪声和$f$无关，所以$f(\mathbf{x};D)$和$y_D$是两个相互独立的随机变量，所以根据期望的运算性质：$\mathbb{E}[XY]=\mathbb{E}[X]\mathbb{E}[Y]$（其中$X$和$Y$为相互独立的随机变量）可得
    $$\begin{array}{rl}{\mathbb{E}}_D\left[2\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)\cdot y_D\right]& =2{\mathbb{E}}_D\left[f(\mathbf{x};D)\cdot y_D\right]-2\bar{f}(\mathbf{x})\cdot {\mathbb{E}}_D\left[y_D\right]\\ & =2{\mathbb{E}}_D\left[f(\mathbf{x};D)\right]\cdot {\mathbb{E}}_D\left[y_D\right]-2\bar{f}(\mathbf{x})\cdot {\mathbb{E}}_D\left[y_D\right]\\ & =2\bar{f}(\mathbf{x})\cdot {\mathbb{E}}_D\left[y_D\right]-2\bar{f}(\mathbf{x})\cdot {\mathbb{E}}_D\left[y_D\right]\\ & =0\end{array}$$
    所以
    $$\begin{array}{rl}{\mathbb{E}}_D\left[2\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)\left(\bar{f}(\mathbf{x})-y_D\right)\right]& ={\mathbb{E}}_D\left[2\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)\cdot \bar{f}(\mathbf{x})\right]-{\mathbb{E}}_D\left[2\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})\right)\cdot y_D\right]\\ & =0+0\\ & =0\end{array}$$
• 第4-5步：同第1-2步一样，减一个$y$再加一个$y$，属于简单的恒等变形；
• 第5-6步：同第2-3步一样，将最后一项利用期望的运算性质进行展开；
• 第6-7步：因为$\bar{f}(\mathbf{x})$和$y$均为常量，所以根据期望的运算性质可知，第6步中的第2项可化为
  $${\mathbb{E}}_D\left[{\left(\bar{f}(\mathbf{x})-y\right)}^2\right]={\left(\bar{f}(\mathbf{x})-y\right)}^2$$
  同理，第6步中的最后一项可化为
  $$2{\mathbb{E}}_D\left[\left(\bar{f}(\mathbf{x})-y\right)\left(y-y_D\right)\right]=2\left(\bar{f}(\mathbf{x})-y\right){\mathbb{E}}_D\left[\left(y-y_D\right)\right]$$
  由于此时假设噪声的期望为零，也即${\mathbb{E}}_D\left[\left(y-y_D\right)\right]=0$，所以
  $$2{\mathbb{E}}_D\left[\left(\bar{f}(\mathbf{x})-y\right)\left(y-y_D\right)\right]=2\left(\bar{f}(\mathbf{x})-y\right)\cdot 0=0$$

三、概率统计基础知识

3.1 二项分布参数$p$的检验

设某事件发生的概率为$p$，$p$未知，作$m$次独立试验，每次观察该事件是否发生，以$X$记该事件发生的次数，则$X$服从二项分布$B(m,p)$，现根据$X$检验如下假设：
$$\begin{array}{r}{H}_0:p\le p_0\\ H_1:p>p_0\end{array}$$
由二项分布本身的特性可知：$p$越小，$X$取到较小值的概率越大。因此，对于上述假设，一个直观上合理的检验为
$$\phi :\text{当}X\le C\text{时接受}{H}_0,\text{否则就拒绝}{H}_0$$
其中，$C\in N$表示事件最大发生次数。此检验对应的功效函数为
$$\begin{array}{rl}{\beta }_{\phi }(p)& =P(X>C)\\ & =1-P(X\le C)\\ & =1-\sum _{i=0}^C\left(\begin{array}{c}m\\ i\end{array}\right)p^i(1-p{)}^{m-i}\\ & =\sum _{i=C+1}^m\left(\begin{array}{c}m\\ i\end{array}\right)p^i(1-p{)}^{m-i}\end{array}$$
由于“$p$越小，$X$取到较小值的概率越大”可以等价表示为：$P(X\le C)$是关于$p$的减函数（更为严格的数学证明参见参考文献[1]中第二章习题7），所以${\beta }_{\phi }(p)=P(X>C)=1-P(X\le C)$是关于$p$的增函数，那么当$p\le p_0$时，${\beta }_{\phi }(p_0)$即为${\beta }_{\phi }(p)$的上确界。

又因为，根据参考文献[1]中5.1.3的定义1.2可知，检验水平$\alpha$默认取最小可能的水平，所以在给定检验水平$\alpha$时，可以通过如下方程解得满足检验水平$\alpha$的整数$C$：
$$\alpha =\sup \left\{{\beta }_{\phi }(p)\right\}$$
显然，当$p\le p_0$时：
$$\begin{array}{rl}\alpha & =\sup \left\{{\beta }_{\phi }(p)\right\}\\ & ={\beta }_{\phi }(p_0)\\ & =\sum _{i=C+1}^m\left(\begin{array}{c}m\\ i\end{array}\right)p_0^i(1-p_0{)}^{m-i}\end{array}$$
对于此方程，通常不一定正好解得一个整数$C$使得方程成立，较常见的情况是存在这样一个$\overline{C}$使得
$$\begin{array}{r}\sum _{i=\overline{C}+1}^m\left(\begin{array}{c}m\\ i\end{array}\right)p_0^i(1-p_0{)}^{m-i}<\alpha \\ \sum _{i=\overline{C}}^m\left(\begin{array}{c}m\\ i\end{array}\right)p_0^i(1-p_0{)}^{m-i}>\alpha \end{array}$$
此时，$C$只能取$\overline{C}$或者$\overline{C}+1$，若$C$取$\overline{C}$，则相当于升高了检验水平$\alpha$，若$C$取$\overline{C}+1$则相当于降低了检验水平$\alpha$，具体如何取舍需要结合实际情况，但是通常为了减小犯第一类错误的概率，会倾向于令$C$取$\overline{C}+1$。下面考虑如何求解$\overline{C}$：易证${\beta }_{\phi }(p_0)$是关于$C$的减函数，所以再结合上述关于$\overline{C}$的两个不等式易推得
$$\overline{C}=\min C\text{ s.t. }\sum _{i=C+1}^m\left(\begin{array}{c}m\\ i\end{array}\right)p_0^i(1-p_0{)}^{m-i}<\alpha$$

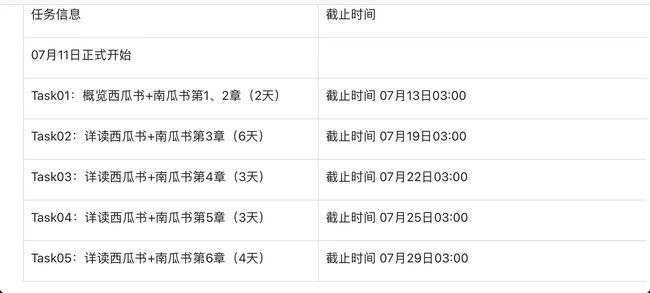
四、时间规划

Reference

[1] 陈希孺编著.概率论与数理统计[M].中国科学技术大学出版社,2009
[2] B 站视频教程：https://www.bilibili.com/video/BV1Mh411e7VU
[3] 线上南瓜书：https://datawhalechina.github.io/pumpkin-book/#/chapter1/chapter1
[4] 开源地址：https://github.com/datawhalechina/pumpkin-book
[5] 周志华《机器学习》版本空间
[6] 周志华老师《机器学习》假设空间和版本空间概念辨析