特征增强SSD算法及其在遥感目标检测中的应用——史文旭

论文阅读笔记

摘要

1. 对SSD的金字塔特征层中的浅层网络设计浅层特征增强模块，以提高浅层网络对小目标物体的特征提取能力；
2. 设计深层特征融合模块，替换SSD金字塔特征层中的深层网络，提高深层网络的特征提取能力；
3. 将提取的图像特征与不同纵横比的候选框进行匹配以执行不同尺度遥感图像目标检测与定位。

0. 引言

1. 反卷积单发检测网络算法（DSSD）(DSSD: Deconvolutional single shot detector)
2. 多尺度单发射击检测增强算法（ESSD）(An enhanced SSD with feature fusion and visual reasoning for object detection)
3. 多尺度单发射击检测特征融合算法（FFSSD）(13)
4. 文献Improved SSD algorithm and its performance analysis of small target detection in remote sensing images基于SSD算法并参考DenseNet网络（title: Densely connected convolutional networks）和特征金字塔（FPN）网络提出改进SSD算法并对遥感图像进行检测，该算法一定程度上提高了遥感图像目标检测的精度，但难以满足实时应用的需求；
5. 文献Fast airplane detection incorporating multi-layer features offully convolutional Networks，全卷积网络多层特征融合的飞机快速检测和 End-to-end airplane detection using transfer learning in remote sensing images基于SSD算法提出了基于多尺度卷积神经网络的飞机目标检测算法，提高了遥感图像中的多尺度飞机目标的检测精度，但检测速度大幅降低，同时该方法对小目标的检测精度较差。

提出了一种特征增强的SSD算法（FESSD），

1. 设计浅层特征增强模块（SFE），通过多分支卷积操作充分提取浅层网络特征，增强浅层网络对遥感图像小目标的特征提取能力;
2. 设计深层特征增强模块（DFE），利用双路径网络提取高深层网络对遥感图像目标的特征提取能力；
3. 设计新的损失函数，提高网络检测性能。

1. 特征增强SSD算法（FESSD）

1.1 SSD算法

浅层网络：Conv4_3, FC7；
深层网络：Conv8_2, Conv9_2, Conv10_2, Conv11_2;

1.2 FESSD算法

1. 参考多分支卷积Inception(title: Going deeper with convolutions)操作和残差网络ResNet(tiltle: Deep residual learning for image recognition)的思想设计浅层特征增强模块（SFE）对Conv4_3、FC7层进行特征增强操作；
2. 参考Dual Path Network(title: Dual path networks)的思想，设计深层特征增强模块（DFE）替换原始SSD算法中的Conv8_2、Conv9_2、Conv10_2、Conv11_2，并命名为DFE_8、DFE_9、DFE_10；
3. 将上述得到的不同尺度的特征送入检测网络，与不同纵横比的候选框进行匹配以适应不同尺度大小的遥感图像目标，并通过NMS操作进行优化处理
   

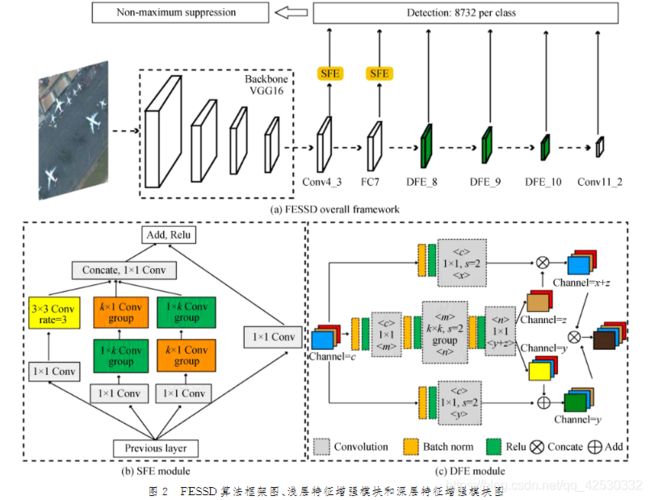
两处改进模块SFE和DFE：

1. SFE：基于多分支卷积操作的思想，使用$1\times 1,3\times 3$的卷积使得网络学习到更多的非线性关系的同时结合残差网络和空洞卷积使网络捕获更多的特征信息，拓宽特征的感受野，此外将$k\times k$卷积分解为$k\times 1$和$1\times k$，在保证感受野大小不变的同时使用分组卷积操作，节省该模块消耗的时间，另一分支的不同之处在于将$k\times 1$和$1\times k$卷积反向组合，将得到的特征结果进行Concate特征融合操作并与残差分支的$1\times 1$卷积结果进行Add特征融合操作。
2. DFE：基于Dual Path Network的思想，并结合残差网络ResNet和密集网络DenseNet对特征提取的特点，不仅深化了整个网络，而且具有从浅层到深层的隐式的特征融合，使得深层网络的特征信息更加丰富，同时使用分组卷积加快模块特征处理效率。

1.3 候选框选择与损失函数

为实现对遥感图像中不同尺度的目标进行检测，设计不同纵横比的候选框进行匹配以适应不同尺度大小的遥感图像目标，假设选取$m$个层的卷积特征用于目标，则第$i$层的特征图候选框尺寸为
$$S_i=S_{min}+\frac{S_{max}-S_{min}}{m-1}(i-1)i\in [1,m]$$
式中，$S_{min}$和$S_{max}$分别取值为$0.2$和$0.95$，表示浅层和深层的候选框与特征图的尺度系数，候选框的宽和高的比取值为$a_r\in \{1,2,3,1/2,1/3\}$，则候选框的宽度为$w_i=S_i\cdot \sqrt{a_r}$，候选框的高为$h_i=S_i/\sqrt{a_r}$，候选框的中心坐标为$(\frac{i+0.5}{|f_k|},\frac{j+0.5}{|f_k|})$，$i,j\in [0,|f_k|]$，其中$|f_k|$表示第$k$个特征的尺寸。

此外，针对模型训练过程中遥感图像正、负样本划分不平衡导致模型退化的问题，本文在SSD算法损失函数的基础上结合聚焦分类损失函数对模型进行优化训练，表示为
$$L(x,c,p,l,g)=\frac{1}{N}[L_{f1}(x,c,p)+a{L}_{loc}(x,l,g)]$$
式中，$N$表示与真实框相匹配的候选框的个数，$x$为输入图像，$c$为目标类别，$p$为预测类别概率，$l$为候选框，$g$代表真实的标签框，$a$为两者的权重，$L_{f1}(x,c,p)$和$L_{loc}(x,l,g)$分别为聚焦分类损失和边框回归损失。其中，$L_{loc}(x,l,g)$借鉴了Faster R-CNN的位置回归函数，表示为
$$L_{loc}(x,l,g)=\sum _{i\in Pos}^N\sum _{m\in c_x,c_y,w,h}{x}_{ij}^{k}smoot{h}_{L_1}(l_i^m-g_j^m)$$
式中，$x_{ij}^k$代表针对类别$k$，第$i$个候选框与第$j$个真实框的结果是否保持一致，若一致则取值为1，否则取值为0.$l_i^m$表示候选框的值，$g_j^m$为真实框的值。

$L_{f1}(x,c,p)$结合聚焦分类损失函数采用交叉熵计算损失，表示为
$$L_{f1}(x,c,p)=-\sum _{i\in Pos}^N{x}_{ij}^{k}plog(c_i^k)-\sum _{i\in neg}(1-p)log(c_j^0)$$
式中，$c_j^0$代表正确且类别为背景预测框的概率，$c_i^k$为利用Softmax函数计算的概率值。