【深度学习】（二）深度学习基础学习笔记

深度学习基础

---

前言

上一章介绍了机器学习的内容，这一章来了解一下深度学习。深度学习是在机器学习的基础上继续研究得来的，又经过了几十年日日夜夜的科研人员的研究，最终留下一些通用的、经典的算法，下面我们开始学习吧。

一、 深度学习与传统机器学习的区别？

网络架构：3层以内—>可达上千层 深度的由来，网络更加深，类比人类的脑细胞更多，深度神经网络能解决的问题也越多
✨层间连接：全连接层—>形式多样：卷积层、池化层 特点：共享权值、跨层反馈等
目标函数：MSE—>CE等
激活函数：Sigmoid/tanh—>ReLu等
️梯度下降算法：GD等—>Adam等
️过拟合抑制：凭经验—>Dropout等

二、深度学习的改进点

1.更加合适目标函数

MSE，均方误差损失是机器学习常用的损失函数，其定义为：

CE，交叉熵误差损失是深度学习常用的损失函数，其定义为：

交叉熵目标函数的最优值搜索空间的“地形”更加“陡峭”，更有利于快速的找的最优值。

2.新增Softmax层

Softmax层的作用是突出最大值并转换成概率形式，类似于max函数，只不过max还是硬最大值，输出唯一的一个最大值，而软最大值是给每一个值一个权值，最大值得权重比例远大于其他值。这样可以解决机器学习Sigmoid函数带来的梯度消失问题。

3.激活函数进化历程

Sigmoid/tanh函数—>2006年RBM预训练—>2015年ReLu函数

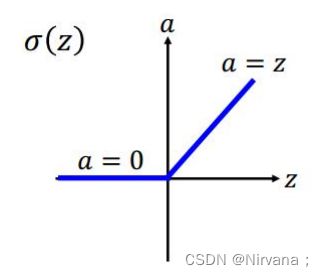
ReLu函数避免了调整各层权重时的梯度消失问题。

4.梯度下降算法进化历程

SGD（存在马鞍面问题）—>Momentum---->Nesterov Momentum->Adagrad(自适应步长)—>RMSprop—>Adam(Nadam)

Adam，自适应矩估计是目前最好的梯度下降算法，本质是带有动量项的RMSprop，利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。它相当于汽车的自动挡很适合新手使用，当然你是老司机也可以使用原始SGD手动调整步长。

5.Batch Normalization的由来

Batch Normalization，简称BatchNorm或BN，翻译为“批归一化”，是神经网络中一种特殊的层，如今已是各种流行网络的标配。在原paper中，BN被建议插入在（每个）ReLU激活层前面。
2015年深度学习领域非常棒的一篇文献提出这一算法：《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》，目前已经被大量的应用，最新的文献算法很多都会引用这个算法，进行网络训练。

BN的核心思想不是为了防止梯度消失或者防止过拟合，其核心是通过对系统参数搜索空间进行约束来增加系统鲁棒性，这种约束压缩了搜索空间，约束也改善了系统的结构合理性，这会带来一系列的性能改善，比如加速收敛，保证梯度，缓解过拟合等。

6.抑制过拟合

主要的三种方法：早期停止训练、权重衰减和Dropout
为了应对神经网络很容易过拟合的问题，2014年 Hinton 提出了Dropout算法，原文《Dropout: A Simple Way to Prevent Neural Networks from Overfitting》。
dropout 是指在深度学习网络的训练过程中，按照一定的概率将一部分神经网络单元暂时从网络中丢弃，相当于从原始的网络中找到一个更瘦的网络。

三、卷积神经网络(CNN)

1.CNN 解决了什么问题？

在 CNN 出现之前，图像对于人工智能来说是一个难题，有2个原因：

• 图像需要处理的数据量太大，导致成本很高，效率很低
• 图像在数字化的过程中很难保留原有的特征，导致图像处理的准确率不高

而CNN的提出很好的解决了这两个问题，对大量的图像数据进行降维的同时进行特征提取。它用类似视觉的方式保留了图像的特征，当图像做翻转，旋转或者变换位置时，它也能有效的识别出来是类似的图像。

2.基本组件

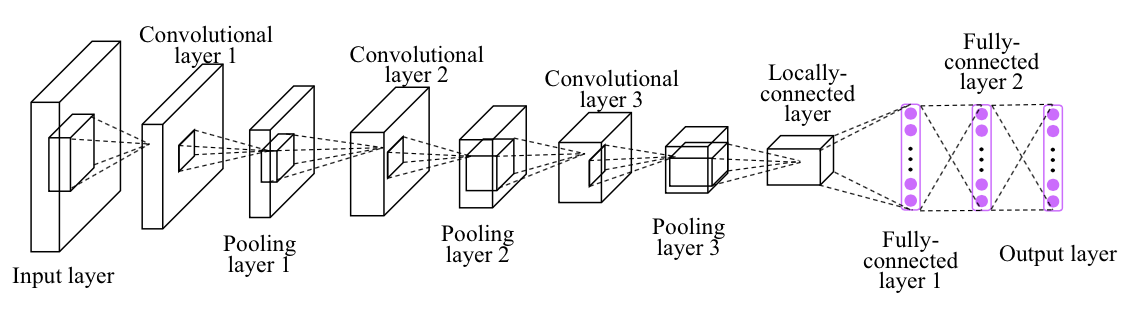
典型的 CNN 由3个部分构成：

• 卷积层– 主要作用是保留图片的特征
• 池化层 – 主要作用是把数据降维，可以有效的避免过拟合
• 全连接层 – 根据不同任务输出我们想要的结果
  

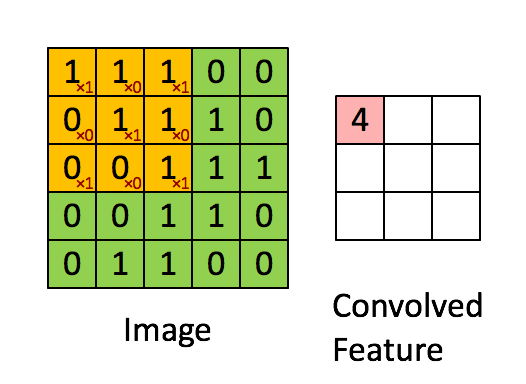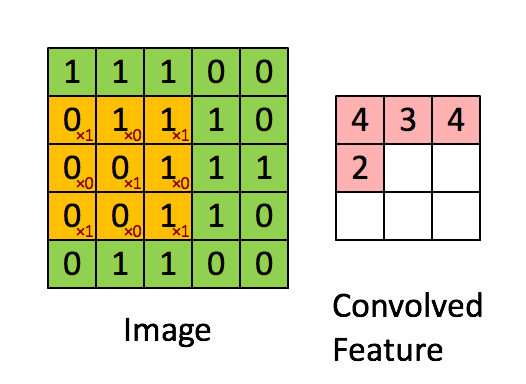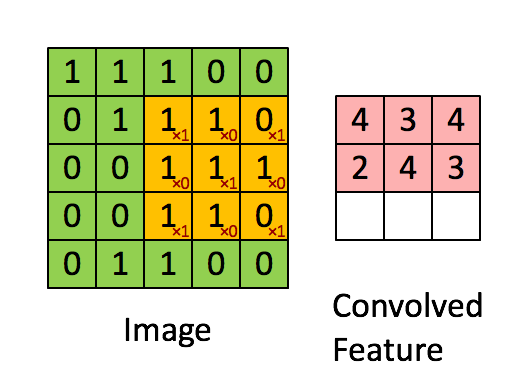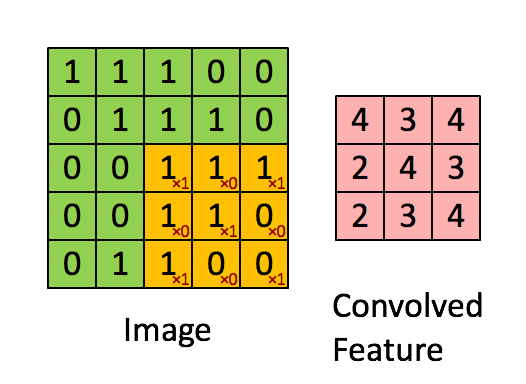
3.卷积层

• 作用：特征提取，卷积层通过卷积核的过滤提取出图片中局部的特征，跟上面提到的人类视觉的特征提取类似。
• 超参数：卷积核数量、核尺寸、步长、零填充
  

# 卷积层，32个卷积核，尺寸为5x5
conv1 = tf.layers.conv2d(x, 32, 5, activation=tf.nn.relu)

4.池化层

• 作用：特征融合，降维
• 无参数需要学习
• 超参数：尺寸、步长、计算类别–最大池化/平均池化

# 最大池化层，步长为2，无需学习任何参量
conv1 = tf.layers.max_pooling2d(conv1, 2, 2)

5.全连接层

• 全连接层采用softmax函数，指数归一化函数，将一个实数向量压缩到（0,1）。
• 最后一个全连接层对接1000类的softmax层（主要取决于标签的种类）

# 展开特征为一维向量，以输入全连接层
fc1 = tf.contrib.layers.flatten(conv2)

# 全连接层
fc1 = tf.layers.dense(fc1, 1024)

# 应用Dropout (训练时打开，测试时关闭)
fc1 = tf.layers.dropout(fc1, rate=dropout, training=is_training)

# 输出层，预测类别
out = tf.layers.dense(fc1, n_classes)

代码实现

开发环境：Python3.9+Tensorflow2.9.1
以经典的手写数字集MNIST识别为例，采用LeNet-5网络。最简单的网络和数据集，之后的网络将会越来越深，数据集会越来越复杂，做好准备
MNIST数据集是机器学习领域中非常经典的一个数据集，由60000个训练样本和10000个测试样本组成，每个样本都是一张28*28像素的灰度手写数字图片。
LeNet 是一系列网络的合称，包括LeNet1 - LeNet5，由Yann LeCun 等人在 1990 年《Handwritten Digit Recognition with a Back-Propagation Network》中提出，是卷积神经网络的 HelloWorld。

# coding: utf-8

# # TensorFlow卷积神经网络(CNN)示例 - 高级API
# ### Convolutional Neural Network Example - tf.layers API

# ## CNN网络结构图示
# 
# ![CNN](http://personal.ie.cuhk.edu.hk/~ccloy/project_target_code/images/fig3.png)
# 
# ## MNIST数据库
# 
# ![MNIST Dataset](http://neuralnetworksanddeeplearning.com/images/mnist_100_digits.png)
# 
# More info: http://yann.lecun.com/exdb/mnist/

from __future__ import division, print_function, absolute_import

# Import MNIST data，MNIST数据集导入
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets("/tmp/data/", one_hot=False)

import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np


# Training Parameters，超参数
learning_rate = 0.001  # 学习率
num_steps = 2000  # 训练步数
batch_size = 128  # 训练数据批的大小

# Network Parameters，网络参数
num_input = 784  # MNIST数据输入 (img shape: 28*28)
num_classes = 10  # MNIST所有类别 (0-9 digits)
dropout = 0.75  # Dropout, probability to keep units，保留神经元相应的概率




# Create the neural network，创建深度神经网络
def conv_net(x_dict, n_classes, dropout, reuse, is_training):
    # Define a scope for reusing the variables，确定命名空间
    with tf.variable_scope('ConvNet', reuse=reuse):
        # TF Estimator类型的输入为像素
        x = x_dict['images']

        # MNIST数据输入格式为一位向量，包含784个特征 (28*28像素)
        # 用reshape函数改变形状以匹配图像的尺寸 [高 x 宽 x 通道数]
        # 输入张量的尺度为四维: [(每一)批数据的数目, 高，宽，通道数]
        x = tf.reshape(x, shape=[-1, 28, 28, 1])

        # 卷积层，32个卷积核，尺寸为5x5
        conv1 = tf.layers.conv2d(x, 32, 5, activation=tf.nn.relu)
        # 最大池化层，步长为2，无需学习任何参量
        conv1 = tf.layers.max_pooling2d(conv1, 2, 2)

        # 卷积层，32个卷积核，尺寸为5x5
        conv2 = tf.layers.conv2d(conv1, 64, 3, activation=tf.nn.relu)
        # 最大池化层，步长为2，无需学习任何参量
        conv2 = tf.layers.max_pooling2d(conv2, 2, 2)

        # 展开特征为一维向量，以输入全连接层
        fc1 = tf.contrib.layers.flatten(conv2)

        # 全连接层
        fc1 = tf.layers.dense(fc1, 1024)
        # 应用Dropout (训练时打开，测试时关闭)
        fc1 = tf.layers.dropout(fc1, rate=dropout, training=is_training)

        # 输出层，预测类别
        out = tf.layers.dense(fc1, n_classes)

    return out

# 确定模型功能 (参照TF Estimator模版)
def model_fn(features, labels, mode):
    # 构建神经网络
    # 因为dropout在训练与测试时的特性不一，我们此处为训练和测试过程创建两个独立但共享权值的计算图
    logits_train = conv_net(features, num_classes, dropout, reuse=False, is_training=True)
    logits_test = conv_net(features, num_classes, dropout, reuse=True, is_training=False)

    # 预测
    pred_classes = tf.argmax(logits_test, axis=1)
    pred_probas = tf.nn.softmax(logits_test)

    if mode == tf.estimator.ModeKeys.PREDICT:
        return tf.estimator.EstimatorSpec(mode, predictions=pred_classes)

        # 确定误差函数与优化器
    loss_op = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(
        logits=logits_train, labels=tf.cast(labels, dtype=tf.int32)))
    optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
    train_op = optimizer.minimize(loss_op, global_step=tf.train.get_global_step())

    # 评估模型精确度
    acc_op = tf.metrics.accuracy(labels=labels, predictions=pred_classes)

    # TF Estimators需要返回EstimatorSpec
    estim_specs = tf.estimator.EstimatorSpec(
        mode=mode,
        predictions=pred_classes,
        loss=loss_op,
        train_op=train_op,
        eval_metric_ops={'accuracy': acc_op})

    return estim_specs

if __name__ == "__main__":
	# 构建Estimator
	model = tf.estimator.Estimator(model_fn)
	
	# 确定训练输入函数
	input_fn = tf.estimator.inputs.numpy_input_fn(
	    x={'images': mnist.train.images}, y=mnist.train.labels,
	    batch_size=batch_size, num_epochs=None, shuffle=True)
	# 开始训练模型
	model.train(input_fn, steps=num_steps)
	
	# 评判模型
	# 确定评判用输入函数
	input_fn = tf.estimator.inputs.numpy_input_fn(
	    x={'images': mnist.test.images}, y=mnist.test.labels,
	    batch_size=batch_size, shuffle=False)
	model.evaluate(input_fn)
	
	# 预测单个图像
	n_images = 4
	# 从数据集得到测试图像
	test_images = mnist.test.images[:n_images]
	# 准备输入数据
	input_fn = tf.estimator.inputs.numpy_input_fn(
	    x={'images': test_images}, shuffle=False)
	# 用训练好的模型预测图片类别
	preds = list(model.predict(input_fn))
	
	# 可视化显示
	for i in range(n_images):
	    plt.imshow(np.reshape(test_images[i], [28, 28]), cmap='gray')
	    plt.show()
	    print("Model prediction:", preds[i])

总结

对于图像处理来说，深度学习只需掌握CNN即可。下一节开始介绍近年来火爆的原始CNN基础上不断改进的神经网络模型，敬请期待