0. 前言
本节中,我们使用策略梯度算法解决 CartPole 问题。虽然在这个简单问题中,使用随机搜索策略和爬山算法就足够了。但是,我们可以使用这个简单问题来更专注的学习策略梯度算法,并在之后的学习中使用此算法解决更加复杂的问题。
1. 策略梯度算法
策略梯度算法通过记录回合中的所有时间步并基于回合结束时与这些时间步相关联的奖励来更新权重训练智能体。使智能体遍历整个回合然后基于获得的奖励更新策略的技术称为蒙特卡洛策略梯度。
在策略梯度算法中,模型权重在每个回合结束时沿梯度方向移动。关于梯度的计算,我们将在下一节中详细解释。此外,在每一时间步中,基于当前状态和权重计算的概率得到策略,并从中采样一个动作。与随机搜索和爬山算法(通过采取确定性动作以获得更高的得分)相反,它不再确定地采取动作。因此,策略从确定性转变为随机性。例如,如果向左的动作和向右的动作的概率为 [0.8,0.2],则表示有 80% 的概率选择向左的动作,但这并不意味着一定会选择向左的动作。
2. 使用策略梯度算法解决CartPole问题
在本节中,我们将学习使用 PyTorch 实现策略梯度算法了。 导入所需的库,创建 CartPole 环境实例,并计算状态空间和动作空间的尺寸:
import gym
import torch
import matplotlib.pyplot as plt
env = gym.make('CartPole-v0')
n_state = env.observation_space.shape[0]
print(n_state)
n_action = env.action_space.n
print(n_action)
定义 run_episode 函数,在此函数中,根据给定输入权重的情况下模拟一回合 CartPole 游戏,并返回奖励和计算出的梯度。在每个时间步中执行以下操作:
- 根据当前状态和输入权重计算两个动作的概率
probs - 根据结果概率采样一个动作
action - 以概率作为输入计算
softmax函数的导数d_softmax,由于只需要计算与选定动作相关的导数,因此:
\frac {\partial p_i} {\partial z_j} = p_i(1-p_j), i=j∂zj∂pi=pi(1−pj),i=j
- 将所得的导数
d_softmax除以概率probs,以得与策略相关的对数导数d_log - 根据链式法则计算权重的梯度
grad:
\frac {dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}dxdy=dudy⋅dxdu
- 记录得到的梯度
grad - 执行动作,累积奖励并更新状态
def run_episode(env, weight):
state = env.reset()
grads = []
total_reward = 0
is_done = False
while not is_done:
state = torch.from_numpy(state).float()
# 根据当前状态和输入权重计算两个动作的概率 probs
z = torch.matmul(state, weight)
probs = torch.nn.Softmax(dim=0)(z)
# 根据结果概率采样一个动作 action
action = int(torch.bernoulli(probs[1]).item())
# 以概率作为输入计算 softmax 函数的导数 d_softmax
d_softmax = torch.diag(probs) - probs.view(-1, 1) * probs
# 计算与策略相关的对数导数d_log
d_log = d_softmax[action] / probs[action]
# 计算权重的梯度grad
grad = state.view(-1, 1) * d_log
grads.append(grad)
state, reward, is_done, _ = env.step(action)
total_reward += reward
if is_done:
break
return total_reward, grads
回合完成后,返回在此回合中获得的总奖励以及在各个时间步中计算的梯度信息,用于之后更新权重。
接下来,定义要运行的回合数,在每个回合中调用 run_episode 函数,并初始化权重以及用于记录每个回合总奖励的变量:
n_episode = 1000 weight = torch.rand(n_state, n_action) total_rewards = []
在每个回合结束后,使用计算出的梯度来更新权重。对于回合中的每个时间步,权重都根据学习率、计算出的梯度和智能体在剩余时间步中的获得的总奖励进行更新。
我们知道在回合终止之前,每一时间步的奖励都是 1。因此,我们用于计算每个时间步策略梯度的未来奖励是剩余的时间步数。在每个回合之后,我们使用随机梯度上升方法将梯度乘以未来奖励来更新权重。这样,一个回合中经历的时间步越长,权重的更新幅度就越大,这将增加获得更大总奖励的机会。我们设定学习率为 0.001:
learning_rate = 0.001
for e in range(n_episode):
total_reward, gradients = run_episode(env, weight)
print('Episode {}: {}'.format(e + 1, total_reward))
for i, gradient in enumerate(gradients):
weight += learning_rate * gradient * (total_reward - i)
total_rewards.append(total_reward)
然后,我们计算通过策略梯度算法获得的平均总奖励:
print('Average total reward over {} episode: {}'.format(n_episode, sum(total_rewards)/n_episode))
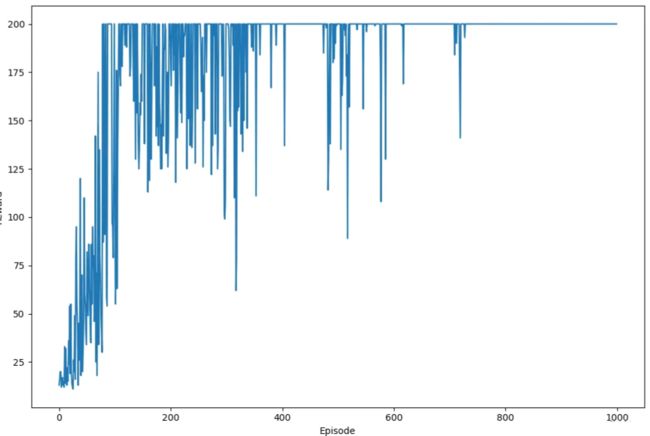
我们可以绘制每个回合的总奖励变化情况,如下所示:
plt.plot(total_rewards)
plt.xlabel('Episode')
plt.ylabel('Reward')
plt.show()
在上图中,我们可以看到奖励会随着训练回合的增加呈现出上升趋势,然后能够在最大值处稳定。我们还可以看到,即使在收敛之后,奖励也会振荡,这是由于策略梯度算法是一种随机策略算法。
最后,我们查看学习到策略在 1000 个新回合中的性能表现,并计算平均奖励:
n_episode_eval = 1000
total_rewards_eval = []
for e in range(n_episode_eval):
total_reward, _ = run_episode(env, weight)
print('Episode {}: {}'.format(e+1, total_reward))
total_rewards_eval.append(total_reward)
print('Average total reward over {} episode: {}'.format(n_episode_eval, sum(total_rewards_eval)/n_episode_eval))
# Average total reward over 1000 episode: 200
进行测试后,可以看到回合的平均奖励接近最大值 200。可以多次测试训练后的模型,得到的平均奖励较为稳定。正如我们一开始所说的那样,对于诸如 CartPole 之类的简单环境,策略梯度算法可能大材小用,但它为我们解决更加复杂的问题奠定了基础。
到此这篇关于PyTorch策略梯度算法详情的文章就介绍到这了,更多相关PyTorch梯度算法内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!