金融相关时间序列分析全指南
来源:yv.l1.pnn - kesci.com
原文链接:时间序列分析入门,看这一篇就够了
点击以上链接 不用配置环境,直接在线运行
数据集下载:DJIA 30股票时间序列
本文包含时间序列的数据结构、可视化、统计学理论及模型介绍,主要侧重金融相关数据实践。翻译自:kaggle - everything you can do with a time series
# 导入必要的包
import os
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
# Above is a special style template for matplotlib, highly useful for visualizing time series data
%matplotlib inline
from pylab import rcParams
from plotly import tools
import plotly.plotly as py
from plotly.offline import init_notebook_mode, iplot
init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.figure_factory as ff
import statsmodels.api as sm
from numpy.random import normal, seed
from scipy.stats import norm
from statsmodels.tsa.arima_model import ARMA
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima_process import ArmaProcess
from statsmodels.tsa.arima_model import ARIMA
import math
from sklearn.metrics import mean_squared_error
print(os.listdir("../input"))
Matplotlib is building the font cache using fc-list. This may take a moment.
['DJIA3716', 'djia307822']
1.介绍日期与时间
1.1 导入时间序列数据
使用的数据
- Google Stocks Data
- Humidity in different world cities
- Microsoft Stocks Data
- Pressure in different world cities
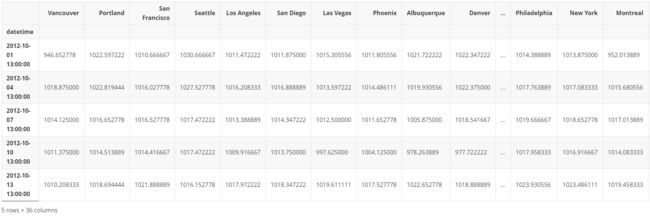
这里使用parse_dates参数将所需的时间序列列导入为datetime列,并使用index_col参数将其选择为数据框的索引。
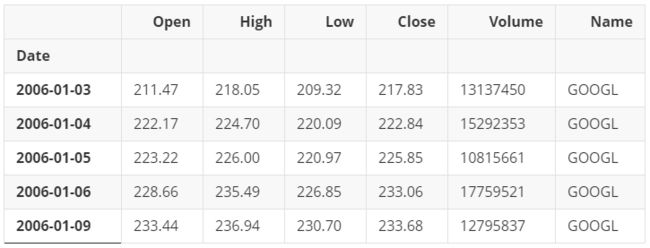
google = pd.read_csv('/home/kesci/input/DJIA3716/GOOGL_2006-01-01_to_2018-01-01.csv',
index_col='Date', parse_dates=['Date'])
google.head()
1.2 清洗以及准备时间序列数据
如何准备数据?
Google 数据没有缺失值,所以我们这里不用处理缺失值。如果有缺失值的话,我们可以使用 fillna() 方法并设置参数 ffill 来填充缺失值。
该参数 ffill 意味着用空白处前面的的最后一个的有效观察值来填补缺失值。
google.isnull().any()
Open False
High False
Low False
Close False
Volume False
Name False
dtype: bool
google.isnull().sum()
Open 0
High 0
Low 0
Close 0
Volume 0
Name 0
dtype: int64
以上代码表示这几列都没有缺失值。
1.3 可视化数据集
plt.figure()
google['2008':'2010'].plot(subplots=True, figsize=(10,12))
plt.title('2008年至2010年Google股票各个属性的表现')
plt.show()
1.4 Timestamps和Periods
什么是timestamps 与 periods? 为什么说他们很有用?
Timestamps 用于表示时间点. Periods 代表时间间隔.
Periods 可用于检查给定期间内是否有特定事件.
它们也可以转换为彼此的形式。
# 创建一个Timestamp
timestamp = pd.Timestamp(2017, 1, 1, 12)
timestamp
Timestamp('2017-01-01 12:00:00')
# 创建一个period
period = pd.Period('2017-01-01')
period
Period('2017-01-01', 'D')
# 检查给定timestamp是否在给定period内
period.start_time < timestamp < period.end_time
True
# timestamp 转换为 period
new_period = timestamp.to_period(freq='H')
new_period
Period('2017-01-01 12:00', 'H')
# period 转换为 timestamp
new_timestamp = period.to_timestamp(freq='H', how='start')
new_timestamp
Timestamp('2017-01-01 00:00:00')
1.5 使用 date_range
什么是 date_range ?
date_range 是一种返回固定频率datetimeindex的方法。
当创建自己的时间序列属性——以用于预先存在的数据,或围绕您创建的时间序列属性排列整个数据时,此函数非常有用。
# 创建一个 datetimeindex ,使用日频率(freq 默认是 daily)
dr1 = pd.date_range(start='1/1/18', end='1/9/18')
dr1
DatetimeIndex(['2018-01-01', '2018-01-02', '2018-01-03', '2018-01-04',
'2018-01-05', '2018-01-06', '2018-01-07', '2018-01-08',
'2018-01-09'],
dtype='datetime64[ns]', freq='D')
# 创建一个 datetimeindex ,使用月(month)频率
dr2 = pd.date_range(start='1/1/18', end='1/1/19', freq='M')
dr2
DatetimeIndex(['2018-01-31', '2018-02-28', '2018-03-31', '2018-04-30',
'2018-05-31', '2018-06-30', '2018-07-31', '2018-08-31',
'2018-09-30', '2018-10-31', '2018-11-30', '2018-12-31'],
dtype='datetime64[ns]', freq='M')
# 创建一个 datetimeindex ,并且不指定起始日期,只使用 periods
dr3 = pd.date_range(end='1/4/2014', periods=8)
dr3
DatetimeIndex(['2013-12-28', '2013-12-29', '2013-12-30', '2013-12-31',
'2014-01-01', '2014-01-02', '2014-01-03', '2014-01-04'],
dtype='datetime64[ns]', freq='D')
# 创建一个 datetimeindex ,并且指定起始日期,终止日期与 periods
dr4 = pd.date_range(start='2013-04-24', end='2014-11-27', periods=3)
dr4
DatetimeIndex(['2013-04-24', '2014-02-09', '2014-11-27'], dtype='datetime64[ns]', freq=None)
1.6 使用 to_datetime
pandas.to_datetime() 用于将参数转换为日期时间。
在这里,DataFrame转换为日期时间Series。
df = pd.DataFrame({'year': [2015, 2016], 'month': [2, 3], 'day': [4, 5]})
df
# 转化为时间Series
df = pd.to_datetime(df)
df
0 2015-02-04
1 2016-03-05
dtype: datetime64[ns]
# 转化为Timestamp
df = pd.to_datetime(df)
df
Timestamp('2017-01-01 00:00:00')
1.7 移动(Shift)和滞后(Lags)
我们可以使用可选的时间频率将索引按所需的周期数移动。
可让我们将时间序列与其自身的过去进行比较时,这很有用
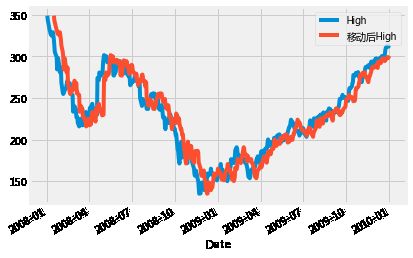
google.loc['2008':'2009'].High.plot(legend=True)
google.loc['2008':'2009'].High.shift(10).plot(legend=True,label='移动后High')
plt.show()
1.8 重新采样(Resampling)
Upsampling - 向上采样,时间序列从低频到高频(每月到每天)重新采样。 它涉及填充或内插丢失的数据
Downsampling - 向下采样,时间序列从高频重新采样到低频(每周一次到每月一次)。 它涉及现有数据的汇总。
这里要用一个极其不完整的数据集来展示
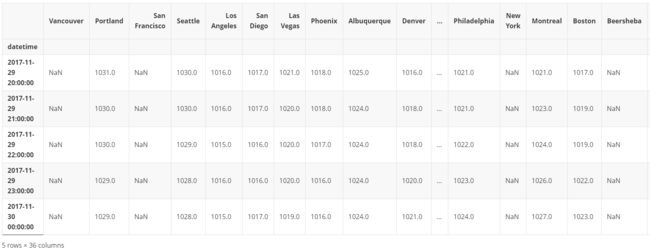
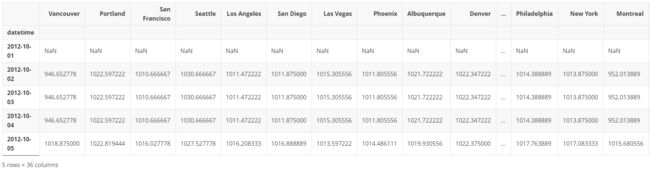
pressure = pd.read_csv('/home/kesci/input/djia307822/pressure.csv',
index_col='datetime', parse_dates=['datetime'])
pressure.tail()
可以看到有非常多的缺失值需要我们去填充
pressure = pressure.iloc[1:]
pressure = pressure.fillna(method='ffill')
pressure.tail()
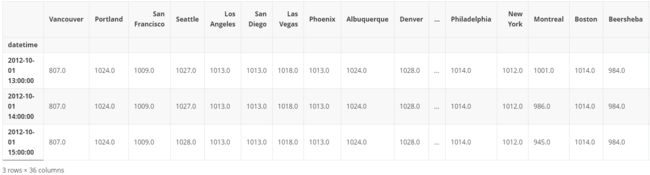
pressure.head(3)
# 向上填充
pressure = pressure.fillna(method='bfill')
pressure.head(3)
解释一下
首先,我们使用 ffill 参数向下填充缺失值。
然后,我们使用 bfill 向上填充缺失值。
# downsampling前查看数据形状
pressure.shape
(45252, 36)
# 使用3日频率进行downsample,这里使用了mean (减少数据量——高频到低频)
pressure = pressure.resample('3D').mean()
pressure.head()
# downsampling后数据形状
pressure.shape
(629, 36)
可以看见,downsample后剩下的行要少得多。
现在,我们将从3天的频率 upsample 到每日频率,即低频到高频
pressure = pressure.resample('D').pad()
pressure.head()
pressure.shape
(1885, 36)
行数再次增加。
如果使用正确,Resample的操作是很酷炫的。
2. 金融与统计
2.1 百分比变化量
# div为除法,shift()表示向后移动一期,这里是一天,因为是日数据
google['Change'] = google.High.div(google.High.shift())
google['Change'].plot(figsize=(20,8))
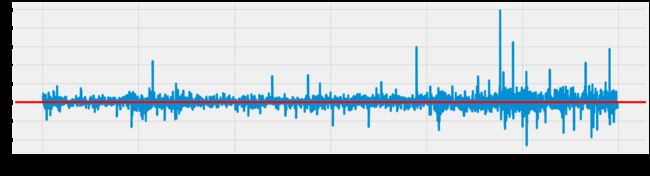
2.2 股票收益
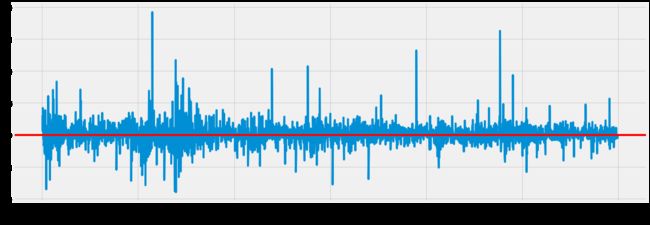
plt.figure()
google['Return'] = google.Change.sub(1).mul(100)
google['Return'].plot(figsize=(20,8))
plt.axhline(y=0, color='r', linestyle='-')
plt.show()
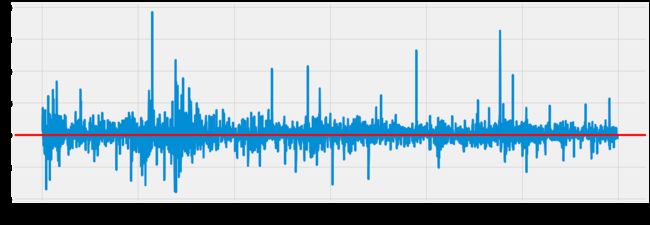
# 另一个计算收益的方法
plt.figure()
google.High.pct_change().mul(100).plot(figsize=(20,6),color='b')
google['Return'].plot(figsize=(20,8))
plt.axhline(y=0, color='r', linestyle='-')
plt.show()
2.3 连续的行中的绝对数值变化
# 用差分
google.High.diff().plot(figsize=(20,6))
plt.axhline(y=0, color='r', linestyle='-')
plt.show()
2.4 比较两个或多个时间序列
我们将通过归一化两个时间序列再进行比较。
这是通过将所有时间序列的每个时间序列元素除以第一个元素来实现的。
这样,两个系列都从同一点开始,可以轻松进行比较。
# 我们将比较微软和Google的股价
microsoft = pd.read_csv('/home/kesci/input/djia307822/MSFT_2006-01-01_to_2018-01-01.csv', index_col='Date', parse_dates=['Date'])
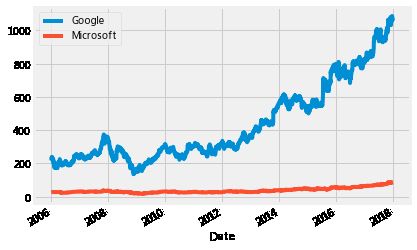
# 可视化
plt.figure()
google.High.plot()
microsoft.High.plot()
plt.legend(['Google','Microsoft'])
plt.show()
# 标准化并进行比较
# 全部都除以第一行的数据
# 两支股票都从100开始
normalized_google = google.High.div(google.High.iloc[0]).mul(100)
normalized_microsoft = microsoft.High.div(microsoft.High.iloc[0]).mul(100)
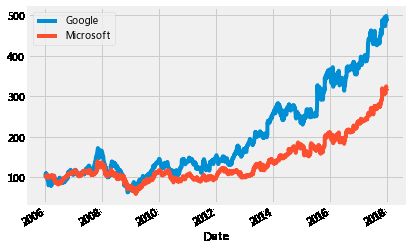
# 可视化
plt.figure()
normalized_google.plot()
normalized_microsoft.plot()
plt.legend(['Google','Microsoft'])
plt.show()
您可以清楚地看到Google在一段时间内的表现胜过微软。
2.5 Window函数
Window 函数用于标识子periods,计算子periods的子度量metrics。
Rolling - 大小相同,且滑动步数相同
Expanding - 包含所有先前值
# Rolling window 函数
# Rolling 90天
rolling_google = google.High.rolling('90D').mean()
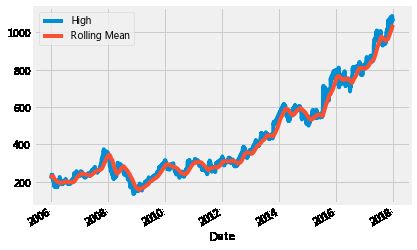
# 与Rolling前数据进行比较
google.High.plot()
rolling_google.plot()
plt.legend(['High','Rolling Mean'])
plt.show()
可看出,Rolling均值图是原始图的平滑版本。
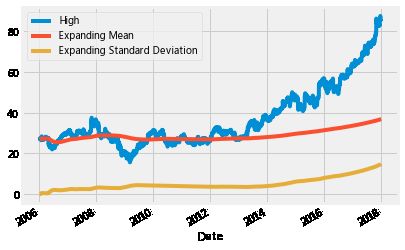
# Expanding window 函数
microsoft_mean = microsoft.High.expanding().mean()
microsoft_std = microsoft.High.expanding().std()
microsoft.High.plot()
microsoft_mean.plot()
microsoft_std.plot()
plt.legend(['High','Expanding Mean','Expanding Standard Deviation'])
plt.show()
2.6 OHLC图
O:代表开盘价
Open H:代表最高价
High L: 代表最低价
Low C: 代表收盘价
OHLC图是显示特定时间段的开盘价,最高价,最低价和收盘价的任何类型的价格图。开盘-高-低-收盘图表(或OHLC图)用作交易工具来可视化和分析证券,货币,股票,债券,商品等随时间的价格变化。
OHLC图可解释当日价格-当今市场的情绪,并通过产生的模式预测未来的价格变化。
OHLC图上的y轴用于价格标度,而x轴是时间标度。在每个单个时间段上,OHLC图都会绘制一个代表两个范围的符号:最高和最低交易价格,以及该单个时间段(例如一天)中的开盘价和收盘价。
在范围符号上,高和低价格范围由主垂直线的长度表示。开盘价和收盘价由刻度线的垂直位置表示,这些刻度线出现在高低垂直线的左侧(代表开盘价)和右侧(代表收盘价)。
可以为每个OHLC图符号分配颜色,以区分市场是“看涨”(收盘价高于开盘价)还是“看涨”(收盘价低于开盘价)。
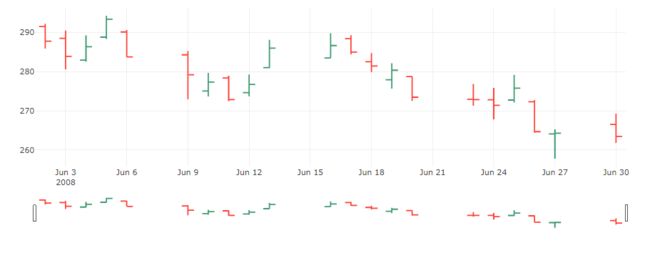
# 2008六月的OHLC图
trace = go.Ohlc(x=google['06-2008'].index,
open=google['06-2008'].Open,
high=google['06-2008'].High,
low=google['06-2008'].Low,
close=google['06-2008'].Close)
data = [trace]
iplot(data, filename='simple_ohlc')
# 2008年OHLC图
trace = go.Ohlc(x=google['2008'].index,
open=google['2008'].Open,
high=google['2008'].High,
low=google['2008'].Low,
close=google['2008'].Close)
data = [trace]
iplot(data, filename='simple_ohlc')
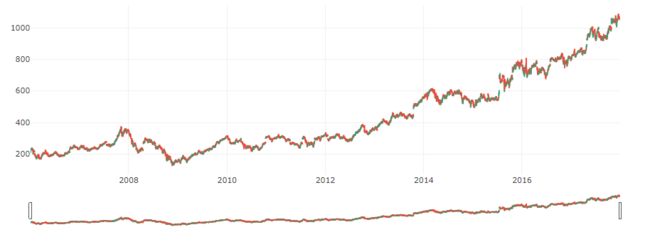
# 2006-2018年OLHC图
trace = go.Ohlc(x=google.index,
open=google.Open,
high=google.High,
low=google.Low,
close=google.Close)
data = [trace]
iplot(data, filename='simple_ohlc')
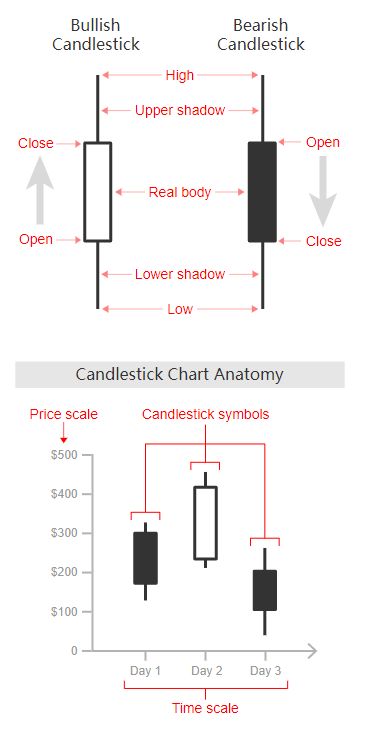
2.7 蜡烛图
这种图表用作交易工具,以可视化和分析证券,衍生工具,货币,股票,债券,商品等随时间的价格变动。尽管烛台图中使用的符号类似于箱形图,但它们的功能不同,不要彼此混淆。
蜡烛图通过使用类似烛台的符号来显示价格信息的多个维度,例如开盘价,收盘价,最高价和最低价。每个符号代表单个时间段(分钟,小时,天,月等)的交易活动。每个烛台符号均沿时间轴绘制在x轴上,以显示一段时间内的交易活动。
蜡烛符号中的主要矩形称为real body,用于显示该时间段的开盘价和收盘价之间的范围。从实体的底部和顶部延伸的线被称为上下阴影(或灯芯)。每个阴影代表所表示的时间段内交易的最高或最低价格。当市场看涨(收盘价高于开盘价)时,机构的颜色通常为白色或绿色。但是,当市场看跌(收盘价低于开盘价)时,机构通常会被涂成黑色或红色。
蜡烛图非常适合检测和预测一段时间内的市场趋势,并且通过每个蜡烛符号的颜色和形状来解释市场的日常情绪很有用。例如,身体越长,销售或购买压力就越大。虽然这是一个非常短的主体,但这表明该时间段内价格变动很小。
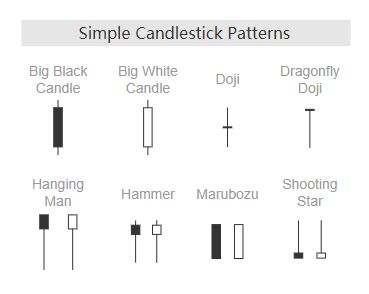
蜡烛图通过各种指标(例如形状和颜色)以及烛台图表中可以找到的许多可识别模式,帮助揭示市场心理(买卖双方所经历的恐惧和贪婪)。总共有42种公认的模式,分为简单模式和复杂模式。烛台图表中的这些模式对于显示价格关系很有用,并可用于预测市场的未来走势。您可以在此处找到每个模式的列表和说明。
请记住,蜡烛图不表示开盘价和收盘价之间发生的事件,仅表示两种价格之间的关系。 因此,您无法确定在那个时间段内交易的波动性。
Source: Datavizcatalogue
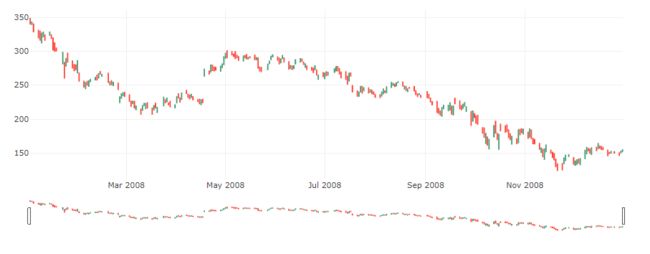
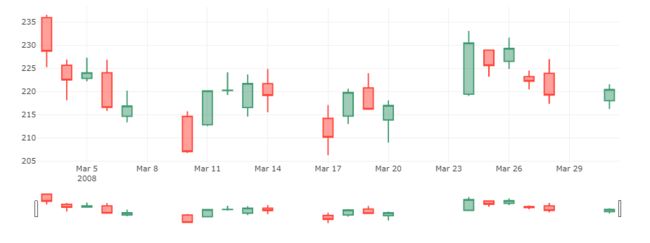
# 2008三月蜡烛图
trace = go.Candlestick(x=google['03-2008'].index,
open=google['03-2008'].Open,
high=google['03-2008'].High,
low=google['03-2008'].Low,
close=google['03-2008'].Close)
data = [trace]
iplot(data, filename='simple_candlestick')
# 2008蜡烛图
trace = go.Candlestick(x=google['2008'].index,
open=google['2008'].Open,
high=google['2008'].High,
low=google['2008'].Low,
close=google['2008'].Close)
data = [trace]
iplot(data, filename='simple_candlestick')
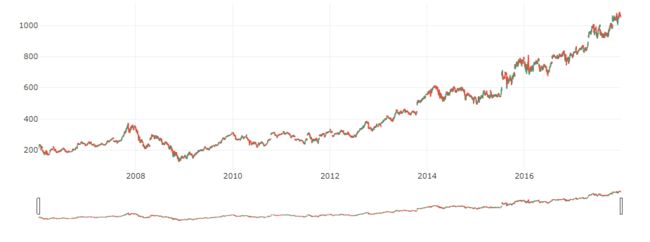
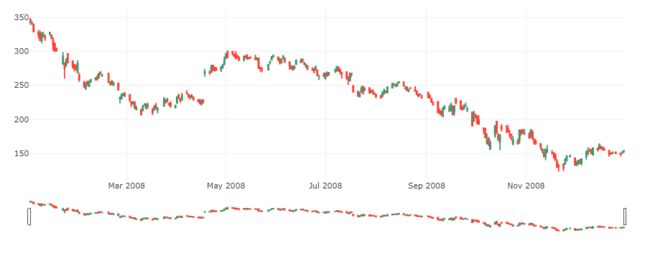
# 2006-2018蜡烛图
trace = go.Candlestick(x=google.index,
open=google.Open,
high=google.High,
low=google.Low,
close=google.Close)
data = [trace]
iplot(data, filename='simple_candlestick')
2.8 自回归系数Autocorrelation与偏自回归系数Partial Autocorrelation
- 自回归系数Autocorrelation - 自相关函数(ACF)可测量序列在不同滞后情况下,与其自身的相关关系。
- 偏自回归系数Partial Autocorrelation - 偏自相关函数在另一角度上可以解释为该序列相对于其过去滞后值的做回归后的回归系数。可以用与标准线性回归相同的方式解释这些术语,即:在使其他滞后(lags)保持不变的同时,特定滞后变化的贡献。
Source: Quora
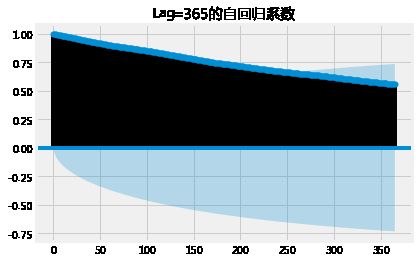
自回归系数Autocorrelation
# Google股票自回归系数
plot_acf(google.High,lags=365,title="Lag=365的自回归系数")
plt.show()
偏自回归系数Partial Autocorrelation
# google票价偏自回归系数
plot_pacf(google.High,lags=365)
plt.show()
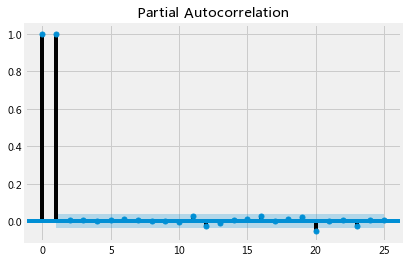
# 微软收盘价的PACF
plot_pacf(microsoft["Close"],lags=25)
plt.show()
在此,只有第0,第1和第20个滞后在统计上是有显著的。
3. 时间序列分解与随机游走
3.1. 趋势、季节性与噪声
这些是时间序列的组成部分
- 趋势 - 时间序列的向上或向下一致的斜率
- 季节性 - 时间序列的清晰周期性模式(例如正弦函数)
- 噪声 - 离群值或缺失值
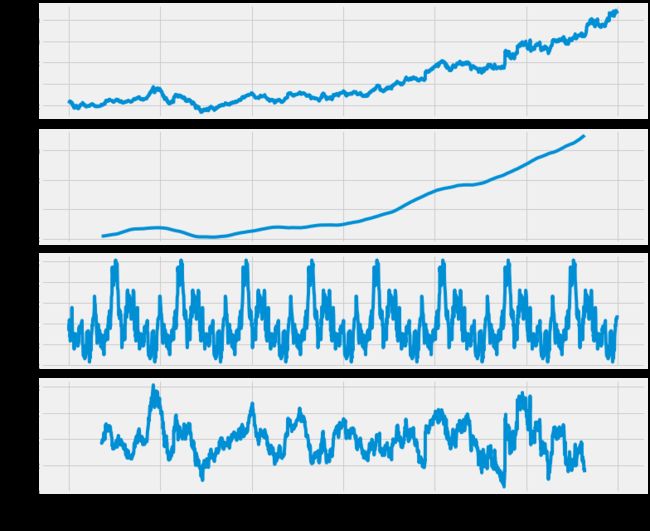
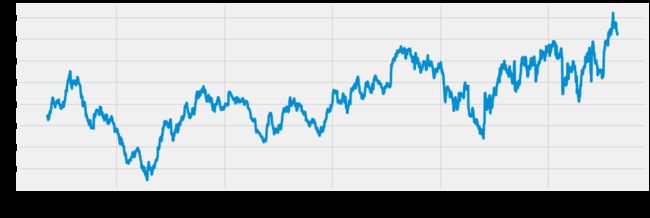
google["High"].plot(figsize=(16,8))
# 现在我们分解它
rcParams['figure.figsize'] = 11, 9
decomposed_google_volume = sm.tsa.seasonal_decompose(google["High"],freq=360)
figure = decomposed_google_volume.plot()
plt.show()
从上面的分解图我们可以看到:
- 上图中明显有上升趋势。
- 还可以看到统一的季节性变化。
- 代表异常值和缺失值的非均匀噪声
3.2. 白噪声
白噪声具有如下性质:
- 恒定均值
- 恒定方差
- 所有滞后之间的相关关系均为0
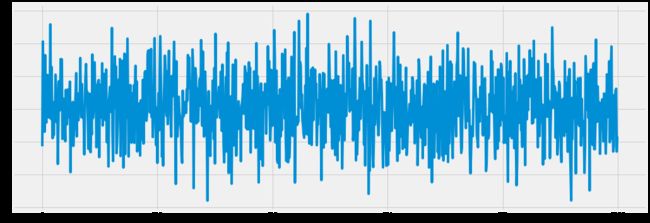
# 画出白噪声
rcParams['figure.figsize'] = 16, 6
white_noise = np.random.normal(loc=0, scale=1, size=1000)
# 以上:loc表示期望,scale表示方差
plt.plot(white_noise)
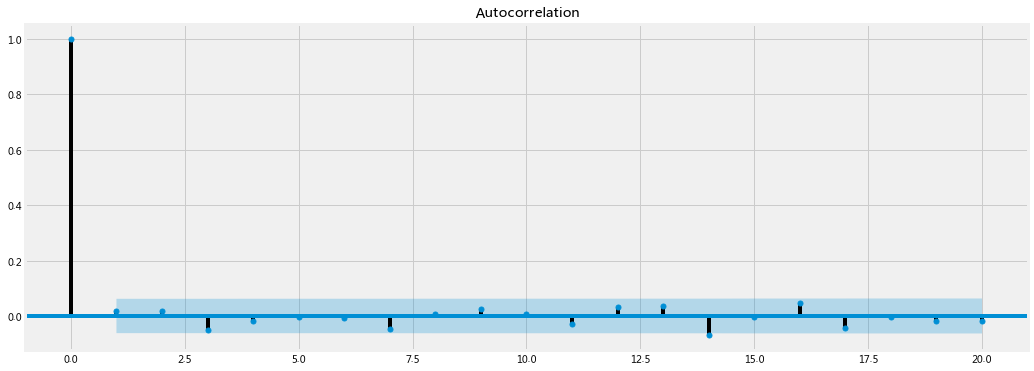
# 白噪声之间的自相关系数图
plot_acf(white_noise,lags=20)
plt.show()
所有滞后在置信区间(阴影部分)内,在统计上不显著
3.3. 随机游走
随机游走是一种数学对象,它描述由某些数学空间(例如整数)上的一系列随机步长构成的路径。
总的来说我们在谈论股票的时候:
今 日 股 价 = 前 一 天 的 股 价 + 噪 声 今日股价 = 前一天的股价 + 噪声 今日股价=前一天的股价+噪声
P t = P t − 1 + ϵ t P_t = P_{t-1}+\epsilon_t Pt=Pt−1+ϵt
随机游走是不能很好地被预测的,因为噪声具有随机性。
有漂移的随机游走
(漂移 μ \mu μ 具有0均值的特性)
P t − P t − 1 = μ + ϵ t P_t - P_{t-1} = \mu + \epsilon_t Pt−Pt−1=μ+ϵt
相关的统计检验
P t = α + β P t − 1 + ϵ t P_t = \alpha + \beta P_{t-1} + \epsilon_t Pt=α+βPt−1+ϵt
上面的式子等价于 P t − P t − 1 = α + β P t − 1 + ϵ t P_t - P_{t-1} = \alpha + \beta P_{t-1} + \epsilon_t Pt−Pt−1=α+βPt−1+ϵt
Test:
- H 0 H_0 H0: β = 1 \beta = 1 β=1 (这是随机游走)
- H 1 H_1 H1: β < 1 \beta < 1 β<1 (这不是随机游走)
Dickey-Fuller Test:
- H 0 H_0 H0: β = 0 \beta = 0 β=0 (这是随机游走)
- H 1 H_1 H1: β < 0 \beta < 0 β<0 (这不是随机游走)
Augmented Dickey-Fuller test
Augmented Dickey-Fuller Test 是一种统计学的检测方法,用于检测一个有某种趋势的时间序列的平稳性。是一种重要的单根检测方法。
其初始假设null hypothesis是该序列不稳定(存在单位根),检测可以有两种途径:
- 一是统计量小于特定拒绝域值;
- 二是p-value大于相应域值。如果是,则拒绝假设,认为序列是稳定的。
# 对谷歌和微软股票交易量进行Augmented Dickey-Fuller检验
adf = adfuller(microsoft["Volume"])
print("p-value of microsoft: {}".format(float(adf[1])))
adf = adfuller(google["Volume"])
print("p-value of google: {}".format(float(adf[1])))
p-value of microsoft: 0.00032015252776520505
p-value of google: 6.510719605768349e-07
因为微软的 p-value 为 0.0003201525 小于 0.05, 所以拒绝 H 0 H_0 H0,我们有充足理由认为它不是随机游走.
因为谷歌的 p-value 0.0000006510 小于 0.05, 所以拒绝 H 0 H_0 H0,我们有充足理由认为它不是随机游走.
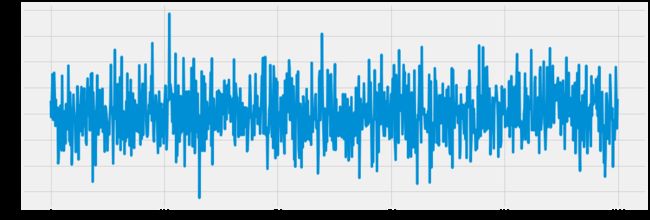
生成随机游走
seed(42)
rcParams['figure.figsize'] = 16, 6
# 从高斯分布生成随机数
random_walk = normal(loc=0, scale=0.01, size=1000)
plt.plot(random_walk)
plt.show()
fig = ff.create_distplot([random_walk],['Random Walk'],bin_size=0.001)
iplot(fig, filename='Basic Distplot')
3.4 平稳性
平稳时间序列是一种统计特性,例如均值,方差,自相关等不论时间怎么变化,他们都是恒定的。
-
强平稳性:是一个随着时间的推移,其无条件联合概率分布不会改变的随机过程。 因此,诸如均值和方差之类的参数也不会随时间变化而变化。其条件性非常强,一般很难满足。
-
弱平稳性:在整个过程中,均值,方差,自相关都是“恒定”的过程
平稳性很重要,因为依赖时间的非平稳序列具有太多的参数,无法在对时间序列建模时考虑到。
diff()(差分)方法可以轻松地将非平稳序列转换为平稳序列。
我们将尝试解析出上述分解后的时间序列中的季节成分。
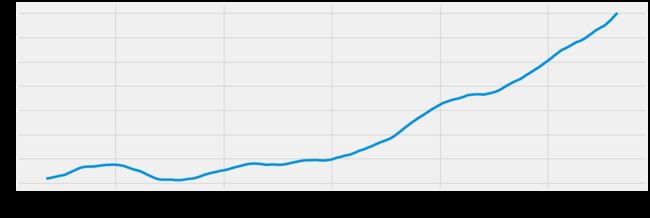
# 绘制原始的非平稳时间序列
decomposed_google_volume.trend.plot()
# 新的平稳的时间序列(使用diff()做了一阶差分)
decomposed_google_volume.trend.diff().plot()
4. 用统计工具建模
建议记住统计模型的英文名称即可,不必纠结其中文译名
4.1 AR 模型
自回归模型(AR)模型是一种随机过程的表示; 因此,自回归模型指定输出变量线性地依赖于其自身的先前值和随机项(一个不完全可预测的项)。 因此该模型采用随机差分方程的形式来表示。
AR(1)
R t = μ + ϕ R t − 1 + ϵ t R_t = \mu + \phi R_{t-1} + \epsilon_t Rt=μ+ϕRt−1+ϵt
由于公式右边只有一阶滞后项( R t − 1 R_{t-1} Rt−1),这也成为在时间 t t t 的一阶 AR模型,其中 μ \mu μ 是常数而 ϵ \epsilon ϵ 是随机游走
如果 ϕ = 1 \phi = 1 ϕ=1, 那么它是随机游走.
如果 ϕ = 0 \phi = 0 ϕ=0, 它是白噪声.
如果 − 1 < ϕ < 1 -1 < \phi < 1 −1<ϕ<1, 它是平稳的.
如果 ϕ \phi ϕ 是 -ve, 存在均值回归.
如果 ϕ \phi ϕ 是 +ve, 存在动量.
AR(2)
R t = μ + ϕ 1 R t − 1 + ϕ 2 R t − 2 + ϵ t R_t = \mu + \phi_1 R_{t-1} + \phi_2 R_{t-2} + \epsilon_t Rt=μ+ϕ1Rt−1+ϕ2Rt−2+ϵt
AR(3)
R t = μ + ϕ 1 R t − 1 + ϕ 2 R t − 2 + ⋯ + ϕ p R t − p + ϵ t R_t = \mu + \phi_1 R_{t-1} + \phi_2 R_{t-2} + \cdots + \phi_p R_{t-p} + \epsilon_t Rt=μ+ϕ1Rt−1+ϕ2Rt−2+⋯+ϕpRt−p+ϵt
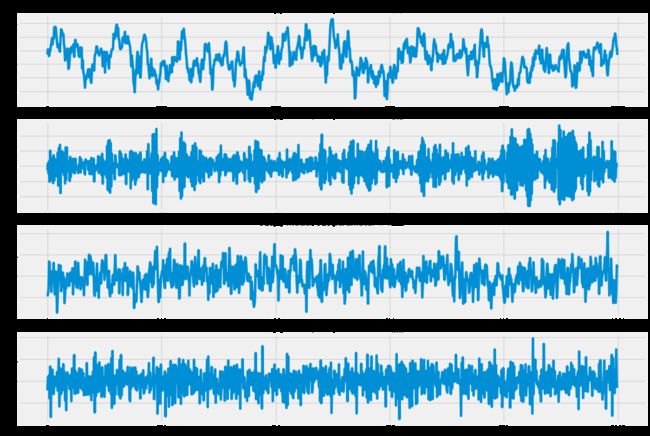
模拟 AR(1) 过程
# AR(1) model:AR parameter = +0.9
rcParams['figure.figsize'] = 16, 12
plt.subplot(4,1,1)
ar1 = np.array([1, -0.9]) # We choose -0.9 as AR parameter is +0.9
ma1 = np.array([1])
AR1 = ArmaProcess(ar1, ma1)
sim1 = AR1.generate_sample(nsample=1000)
plt.title('AR(1) model: AR parameter = +0.9')
plt.plot(sim1)
# 后面会介绍MA(q)模型
# AR(1) MA(1) AR parameter = -0.9
plt.subplot(4,1,2)
ar2 = np.array([1, 0.9]) # We choose +0.9 as AR parameter is -0.9
ma2 = np.array([1])
AR2 = ArmaProcess(ar2, ma2)
sim2 = AR2.generate_sample(nsample=1000)
plt.title('AR(1) model: AR parameter = -0.9')
plt.plot(sim2)
# AR(2) MA(1) AR parameter = 0.9
plt.subplot(4,1,3)
ar3 = np.array([2, -0.9]) # 我们选择 -0.9 作为 AR 参数: +0.9
ma3 = np.array([1])
AR3 = ArmaProcess(ar3, ma3)
sim3 = AR3.generate_sample(nsample=1000)
plt.title('AR(2) model: AR parameter = +0.9')
plt.plot(sim3)
# AR(2) MA(1) AR parameter = -0.9
plt.subplot(4,1,4)
ar4 = np.array([2, 0.9]) # 我们选择 +0.9 作为 AR 参数: -0.9
ma4 = np.array([1])
AR4 = ArmaProcess(ar4, ma4)
sim4 = AR4.generate_sample(nsample=1000)
plt.title('AR(2) model: AR parameter = -0.9')
plt.plot(sim4)
plt.show()
预测
model = ARMA(sim1, order=(1,0))
result = model.fit()
print(result.summary())
print("μ={} ,ϕ={}".format(result.params[0],result.params[1]))
ARMA Model Results
==============================================================================
Dep. Variable: y No. Observations: 1000
Model: ARMA(1, 0) Log Likelihood -1415.701
Method: css-mle S.D. of innovations 0.996
Date: Wed, 16 Oct 2019 AIC 2837.403
Time: 05:23:12 BIC 2852.126
Sample: 0 HQIC 2842.998
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.7072 0.288 2.454 0.014 0.142 1.272
ar.L1.y 0.8916 0.014 62.742 0.000 0.864 0.919
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.1216 +0.0000j 1.1216 0.0000
-----------------------------------------------------------------------------
μ=0.707201867170821 ,ϕ=0.8915815672242373
ϕ \phi ϕ 在 0.9 附近,我们可以选其作为我们AR模型的参数。
预测模型
# Predicting simulated AR(1) model
result.plot_predict(start=900, end=1010)
plt.show()
rmse = math.sqrt(mean_squared_error(sim1[900:1011], result.predict(start=900,end=999)))
print("The root mean squared error is {}.".format(rmse))
The root mean squared error is 1.0408054564799076.
y 是预测结果的可视化
# 预测Minneapolis的气压水平
humid = ARMA(pressure['Minneapolis'].diff().iloc[2:].values, order=(1,0))
res = humid.fit()
res.plot_predict(start=1000, end=1100)
plt.show()
再试试谷歌股票
# Predicting closing prices of google
humid = ARMA(google["Close"].diff().iloc[1:].values, order=(1,0))
res = humid.fit()
res.plot_predict(start=900, end=1010)
plt.show()
也许会有更好的模型
4.2 MA 模型
即移动平均模型 (MA) model专门针对单变量时间序列建模。
移动平均模型指定输出变量线性地取决于随机(不完全可预测)项的当前值和各种过去值。
MA(1)
R t = μ + ϵ t + θ ϵ t − 1 R_t = \mu + \epsilon_t + \theta \epsilon_{t-1} Rt=μ+ϵt+θϵt−1
可理解为 今 日 回 报 = 均 值 + 今 日 噪 声 + 前 一 天 的 噪 声 今日回报 = 均值 + 今日噪声 + 前一天的噪声 今日回报=均值+今日噪声+前一天的噪声
因为等式右边只有一阶滞后项, 所以此为一阶MA过程。
模拟 MA(1)
rcParams['figure.figsize'] = 16, 6
ar1 = np.array([1])
ma1 = np.array([1, -0.5])
MA1 = ArmaProcess(ar1, ma1)
sim1 = MA1.generate_sample(nsample=1000)
plt.plot(sim1)
预测模拟的 MA 模型
model = ARMA(sim1, order=(0,1))
result = model.fit()
print(result.summary())
print("μ={} ,θ={}".format(result.params[0],result.params[1]))
ARMA Model Results
==============================================================================
Dep. Variable: y No. Observations: 1000
Model: ARMA(0, 1) Log Likelihood -1423.276
Method: css-mle S.D. of innovations 1.004
Date: Wed, 16 Oct 2019 AIC 2852.553
Time: 05:30:51 BIC 2867.276
Sample: 0 HQIC 2858.148
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0228 0.014 -1.652 0.099 -0.050 0.004
ma.L1.y -0.5650 0.027 -20.797 0.000 -0.618 -0.512
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
MA.1 1.7699 +0.0000j 1.7699 0.0000
-----------------------------------------------------------------------------
μ=-0.022847164219747917 ,θ=-0.5650012133945569
用 MA 模型做预测
model = ARMA(pressure['Minneapolis'].diff().iloc[2:].values, order=(0,3))
result = model.fit()
print(result.summary())
print("μ={} ,θ={}".format(result.params[0],result.params[1]))
result.plot_predict(start=1000, end=1100)
plt.show()
ARMA Model Results
==============================================================================
Dep. Variable: y No. Observations: 1883
Model: ARMA(0, 3) Log Likelihood -5242.754
Method: css-mle S.D. of innovations 3.915
Date: Wed, 16 Oct 2019 AIC 10495.508
Time: 05:31:42 BIC 10523.212
Sample: 0 HQIC 10505.712
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0003 0.026 0.010 0.992 -0.050 0.050
ma.L1.y -1.101e-06 0.018 -6.06e-05 1.000 -0.036 0.036
ma.L2.y -1.162e-06 0.018 -6.39e-05 1.000 -0.036 0.036
ma.L3.y -0.7176 0.027 -26.450 0.000 -0.771 -0.664
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
MA.1 -0.5585 -0.9673j 1.1170 -0.3333
MA.2 -0.5585 +0.9673j 1.1170 0.3333
MA.3 1.1170 -0.0000j 1.1170 -0.0000
-----------------------------------------------------------------------------
μ=0.0002522391526654763 ,θ=-1.1005662984144147e-06
rmse = math.sqrt(mean_squared_error(pressure['Minneapolis'].diff().iloc[1000:1101].values, result.predict(start=1000,end=1100)))
print("The root mean squared error is {}.".format(rmse))
The root mean squared error is 3.0713710764189415.
4.3 ARMA 模型
自回归移动平均模型 (ARMA) 用两个多项式来简要描述(弱)平稳随机过程,一个多项式用于自回归,第二个多项式用于移动平均值。 它是AR和MA模型的融合。
ARMA(1,1)
R t = μ + ϕ R t − 1 + ϵ t + θ ϵ t − 1 R_t = \mu + \phi R_{t-1} + \epsilon_t + \theta \epsilon_{t-1} Rt=μ+ϕRt−1+ϵt+θϵt−1
基本上
今日回报 = 均值 + 前一天的回报 + 噪声 + 昨天的噪声
使用 ARMA 作预测
# 预测Microsoft库存量
model = ARMA(microsoft["Volume"].diff().iloc[1:].values, order=(3,3))
result = model.fit()
print(result.summary())
print("μ={}, ϕ={}, θ={}".format(result.params[0],result.params[1],result.params[2]))
result.plot_predict(start=1000, end=1100)
plt.show()
ARMA Model Results
==============================================================================
Dep. Variable: y No. Observations: 3018
Model: ARMA(3, 3) Log Likelihood -55408.974
Method: css-mle S.D. of innovations 22751608.082
Date: Wed, 16 Oct 2019 AIC 110833.948
Time: 05:32:58 BIC 110882.047
Sample: 0 HQIC 110851.244
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -2.03e+04 9915.585 -2.047 0.041 -3.97e+04 -863.030
ar.L1.y 0.2053 0.160 1.287 0.198 -0.107 0.518
ar.L2.y 0.7297 0.179 4.081 0.000 0.379 1.080
ar.L3.y -0.1413 0.057 -2.467 0.014 -0.254 -0.029
ma.L1.y -0.8117 0.157 -5.166 0.000 -1.120 -0.504
ma.L2.y -0.7692 0.258 -2.979 0.003 -1.275 -0.263
ma.L3.y 0.5853 0.130 4.494 0.000 0.330 0.841
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 -1.1772 +0.0000j 1.1772 0.5000
AR.2 1.1604 +0.0000j 1.1604 0.0000
AR.3 5.1820 +0.0000j 5.1820 0.0000
MA.1 -1.1579 +0.0000j 1.1579 0.5000
MA.2 1.0075 +0.0000j 1.0075 0.0000
MA.3 1.4647 +0.0000j 1.4647 0.0000
-----------------------------------------------------------------------------
μ=-20297.220675944438, ϕ=0.20526115960300076, θ=0.7297015548306405
rmse = math.sqrt(mean_squared_error(microsoft["Volume"].diff().iloc[1000:1101].values, result.predict(start=1000,end=1100)))
print("The root mean squared error is {}.".format(rmse))
The root mean squared error is 38038294.04431978.
ARMA 模型展现出了比 AR 与 MA 更好的结果.
4.4 ARIMA 模型
自回归综合移动平均(ARIMA)模型是自回归移动平均(ARMA)模型的概括。
这两个模型都适合于时间序列数据,以更好地理解数据或预测序列中的未来点(预测)。
ARIMA模型适用于数据显示出非平稳特性的某些情况,其可以执行一次或多次差分以消除非平稳性。
ARIMA 模型的形式: ARIMA(p,d,q): p 是 AR 参数, d 是差分参数, q 是 MA 参数。
ARIMA(1,0,0)
等价于一阶自回归模型AR(1)
ARIMA(1,0,1)
等价与ARMA(1,1)
ARIMA(1,1,1)
Δ y t = a 1 Δ y t − 1 + ϵ t + b 1 ϵ t − 1 \Delta y_t = a_1 \Delta y_{t-1} + \epsilon_t + b_1 \epsilon_{t-1} Δyt=a1Δyt−1+ϵt+b1ϵt−1
其中 Δ y t = y t − y t − 1 \Delta y_t = y_t - y_{t-1} Δyt=yt−yt−1
使用 ARIMA 做预测
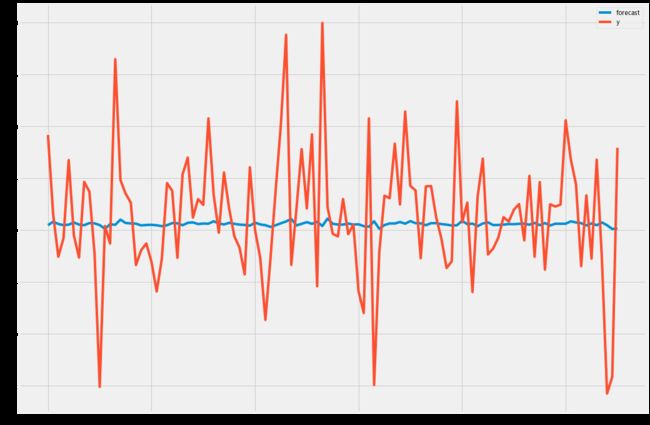
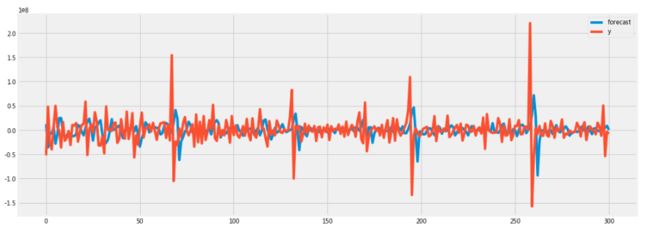
# 预测microsoft股票交易量
rcParams['figure.figsize'] = 16, 6
model = ARIMA(microsoft["Volume"].diff().iloc[1:].values, order=(2,1,0))
result = model.fit()
print(result.summary())
result.plot_predict(start=700, end=1000)
plt.show()
ARIMA Model Results
==============================================================================
Dep. Variable: D.y No. Observations: 3017
Model: ARIMA(2, 1, 0) Log Likelihood -56385.467
Method: css-mle S.D. of innovations 31647215.008
Date: Wed, 16 Oct 2019 AIC 112778.933
Time: 05:33:01 BIC 112802.981
Sample: 1 HQIC 112787.581
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 9984.0302 2.48e+05 0.040 0.968 -4.75e+05 4.95e+05
ar.L1.D.y -0.8716 0.016 -53.758 0.000 -0.903 -0.840
ar.L2.D.y -0.4551 0.016 -28.071 0.000 -0.487 -0.423
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 -0.9575 -1.1315j 1.4823 -0.3618
AR.2 -0.9575 +1.1315j 1.4823 0.3618
-----------------------------------------------------------------------------
rmse = math.sqrt(mean_squared_error(microsoft["Volume"].diff().iloc[700:1001].values, result.predict(start=700,end=1000)))
print("The root mean squared error is {}.".format(rmse))
The root mean squared error is 61937614.65140498.
考虑到轻微的滞后,这是一个很好的模型。
4.5 VAR 模型
向量自回归(VAR)是一种随机过程模型,用于捕获多个时间序列之间的线性相互依赖性。
VAR模型通过允许多个evolving variable来概括单变量AR模型。
VAR中的所有变量都以相同的方式进入模型:每个变量都有一个方程式,该方程式根据其自身的滞后值,其他模型变量的滞后值和误差项来解释其演化。
VAR建模不需要像具有联立方程的结构模型那样,需要了解背后有什么“推力”在影响变量:唯一要求的先验知识是一个假设会在跨时间相互影响的变量列表。
# 预测谷歌和微软的收盘价格
train_sample = pd.concat([google["Close"].diff().iloc[1:],microsoft["Close"].diff().iloc[1:]],axis=1)
model = sm.tsa.VARMAX(train_sample,order=(2,1),trend='c')
result = model.fit(maxiter=1000,disp=False)
print(result.summary())
predicted_result = result.predict(start=0, end=1000)
result.plot_diagnostics()
# 计算误差
rmse = math.sqrt(mean_squared_error(train_sample.iloc[1:1002].values, predicted_result.values))
print("The root mean squared error is {}.".format(rmse))
Statespace Model Results
==============================================================================
Dep. Variable: ['Close', 'Close'] No. Observations: 3018
Model: VARMA(2,1) Log Likelihood -12184.882
+ intercept AIC 24403.764
Date: Wed, 16 Oct 2019 BIC 24505.974
Time: 05:33:18 HQIC 24440.517
Sample: 0
- 3018
Covariance Type: opg
===================================================================================
Ljung-Box (Q): 77.46, 79.29 Jarque-Bera (JB): 48076.50, 14930.54
Prob(Q): 0.00, 0.00 Prob(JB): 0.00, 0.00
Heteroskedasticity (H): 3.31, 1.62 Skew: 1.15, -0.03
Prob(H) (two-sided): 0.00, 0.00 Kurtosis: 22.42, 13.90
Results for equation Close
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
const 0.3663 0.290 1.265 0.206 -0.201 0.934
L1.Close -0.3546 0.534 -0.664 0.507 -1.402 0.693
L1.Close -0.0416 5.614 -0.007 0.994 -11.044 10.961
L2.Close 0.0126 0.034 0.375 0.707 -0.053 0.079
L2.Close 0.3345 0.443 0.755 0.450 -0.533 1.203
L1.e(Close) 0.3946 0.534 0.739 0.460 -0.652 1.441
L1.e(Close) -0.2233 5.642 -0.040 0.968 -11.281 10.835
Results for equation Close
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
const 0.0185 0.028 0.656 0.512 -0.037 0.074
L1.Close 0.0316 0.053 0.591 0.554 -0.073 0.136
L1.Close -0.3797 0.613 -0.619 0.536 -1.582 0.822
L2.Close 0.0016 0.004 0.450 0.653 -0.005 0.009
L2.Close -0.0433 0.044 -0.986 0.324 -0.129 0.043
L1.e(Close) -0.0293 0.053 -0.549 0.583 -0.134 0.075
L1.e(Close) 0.3336 0.614 0.544 0.587 -0.869 1.536
Error covariance matrix
========================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------------
sqrt.var.Close 6.9016 0.041 167.252 0.000 6.821 6.982
sqrt.cov.Close.Close 0.2924 0.005 57.757 0.000 0.282 0.302
sqrt.var.Close 0.4809 0.003 163.163 0.000 0.475 0.487
========================================================================================
The root mean squared error is 3.6743099933249246.
4.6.1 SARIMA models
SARIMA模型对于季节性时间序列的建模非常有用,在季节性时间序列中,给定季节的平均值和其他统计数据在各年中都不是平稳的。定义的SARIMA模型是非季节自回归综合移动平均(ARMA)和自回归移动平均(ARIMA)模型的直接扩展
# Predicting closing price of Google'
train_sample = google["Close"].diff().iloc[1:].values
model = sm.tsa.SARIMAX(train_sample,order=(4,0,4),trend='c')
result = model.fit(maxiter=1000,disp=False)
print(result.summary())
predicted_result = result.predict(start=0, end=500)
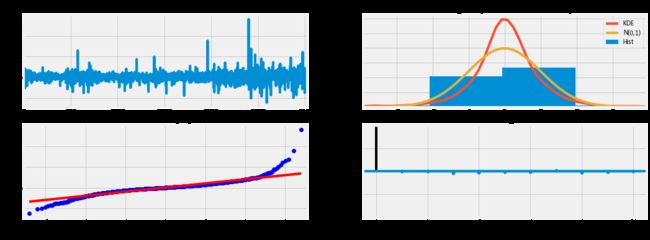
result.plot_diagnostics()
# calculating error
rmse = math.sqrt(mean_squared_error(train_sample[1:502], predicted_result))
print("The root mean squared error is {}.".format(rmse))
Statespace Model Results
==============================================================================
Dep. Variable: y No. Observations: 3018
Model: SARIMAX(4, 0, 4) Log Likelihood -10098.505
Date: Wed, 16 Oct 2019 AIC 20217.009
Time: 05:33:31 BIC 20277.133
Sample: 0 HQIC 20238.629
- 3018
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 0.1014 0.047 2.137 0.033 0.008 0.194
ar.L1 0.1878 0.008 24.882 0.000 0.173 0.203
ar.L2 1.1923 0.006 190.557 0.000 1.180 1.205
ar.L3 0.2170 0.007 32.332 0.000 0.204 0.230
ar.L4 -0.9787 0.008 -127.674 0.000 -0.994 -0.964
ma.L1 -0.1934 0.008 -23.486 0.000 -0.210 -0.177
ma.L2 -1.1942 0.007 -166.466 0.000 -1.208 -1.180
ma.L3 -0.2249 0.008 -28.546 0.000 -0.240 -0.209
ma.L4 0.9738 0.008 116.740 0.000 0.957 0.990
sigma2 47.1073 0.408 115.374 0.000 46.307 47.908
===================================================================================
Ljung-Box (Q): 67.27 Jarque-Bera (JB): 52919.32
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 3.30 Skew: 1.21
Prob(H) (two-sided): 0.00 Kurtosis: 23.37
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
The root mean squared error is 4.398362762846205.
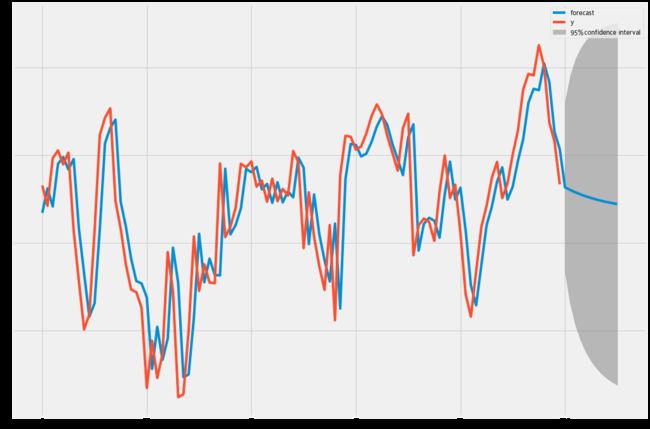
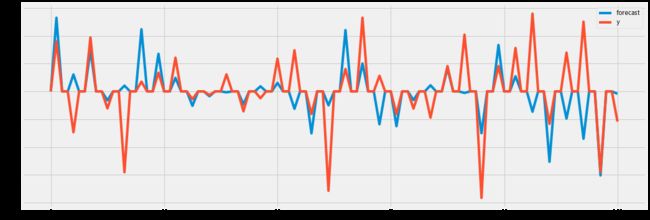
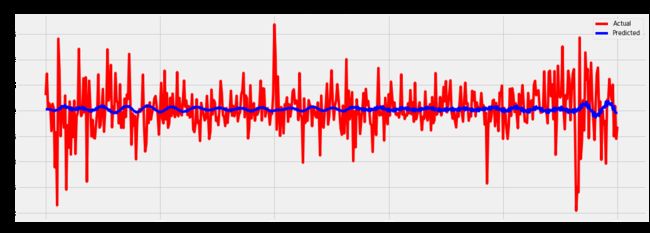
plt.plot(train_sample[1:502],color='red')
plt.plot(predicted_result,color='blue')
plt.legend(['Actual','Predicted'])
plt.title('Google Closing prices')
plt.show()
4.6.3 动态因子模型
动态因子模型是用于多元时间序列的灵活模型,其中观察到的内生变量是外生协变量和未观察因子的线性函数,具有向量自回归结构。
未观察到的因素也可能是外部协变量的函数。
因变量方程中的扰动可能是自相关的。
# 预测微软和谷歌的收盘价
train_sample = pd.concat([google["Close"].diff().iloc[1:],microsoft["Close"].diff().iloc[1:]],axis=1)
model = sm.tsa.DynamicFactor(train_sample, k_factors=1, factor_order=2)
result = model.fit(maxiter=1000,disp=False)
print(result.summary())
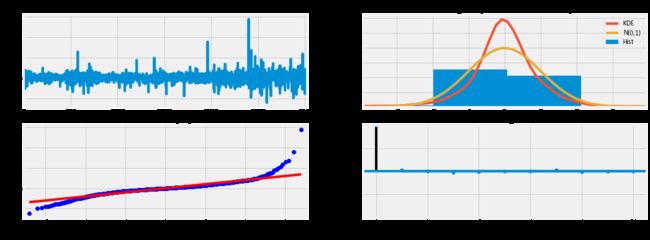
predicted_result = result.predict(start=0, end=1000)
result.plot_diagnostics()
# 计算误差
rmse = math.sqrt(mean_squared_error(train_sample.iloc[1:1002].values, predicted_result.values))
print("The root mean squared error is {}.".format(rmse))
Statespace Model Results
=============================================================================================
Dep. Variable: ['Close', 'Close'] No. Observations: 3018
Model: DynamicFactor(factors=1, order=2) Log Likelihood -12198.578
Date: Wed, 16 Oct 2019 AIC 24409.156
Time: 05:33:39 BIC 24445.230
Sample: 0 HQIC 24422.128
- 3018
Covariance Type: opg
===================================================================================
Ljung-Box (Q): 77.67, 95.04 Jarque-Bera (JB): 48193.46, 15038.05
Prob(Q): 0.00, 0.00 Prob(JB): 0.00, 0.00
Heteroskedasticity (H): 3.36, 1.62 Skew: 1.14, -0.04
Prob(H) (two-sided): 0.00, 0.00 Kurtosis: 22.44, 13.94
Results for equation Close
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
loading.f1 -6.9110 1.822 -3.794 0.000 -10.481 -3.341
Results for equation Close
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
loading.f1 -0.2922 0.077 -3.784 0.000 -0.444 -0.141
Results for factor equation f1
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
L1.f1 0.0292 0.021 1.382 0.167 -0.012 0.071
L2.f1 0.0137 0.016 0.865 0.387 -0.017 0.045
Error covariance matrix
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
sigma2.Close 6.184e-05 25.182 2.46e-06 1.000 -49.355 49.355
sigma2.Close 0.2327 0.045 5.119 0.000 0.144 0.322
================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
The root mean squared error is 3.682205152159832.
可供参考文献:
- Manipulating Time Series Data in Python
- Introduction to Time Series Analysis in Python
- Visualizing Time Series Data in Python
- VAR models and LSTM
- State space models