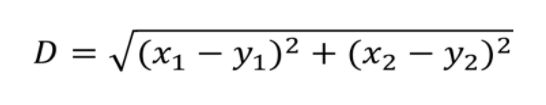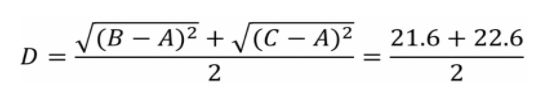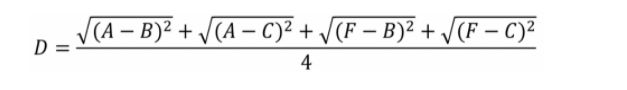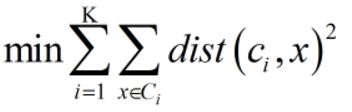人工智能数学基础——聚类分析
1.层次聚类概述
层次聚类
层次聚类(Hierarchical Clustering)是聚类算法的一种,通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树。在聚类树中,不同类别的原始数据点是树的最低层,树的顶层是一个聚类的根节点。创建聚类树有自下而上合并和自上而下分裂两种方法。
作为一家公司的人力资源部经理,你可以把所有的雇员组织成较大的簇,如主管、经理和职员;然后你可以进一步划分为较小的簇,例如,职员簇可以进一步划分为子簇:高级职员,一般职员和实习人员。所有的这些簇形成了层次结构,可以很容易地对各层次上的数据进行汇总或者特征化。
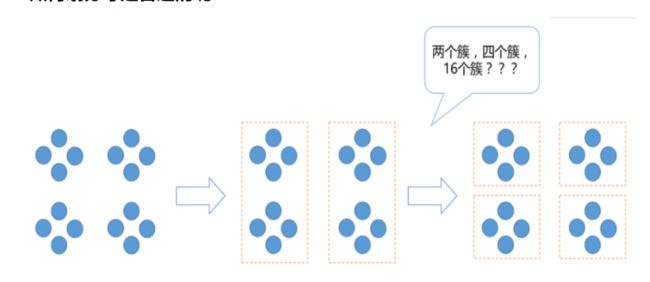
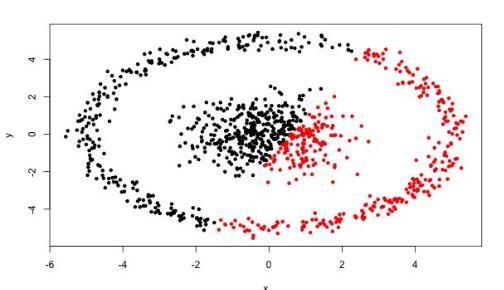
如何划分才是合适的呢?
直观来看,上图中展示的数据划分为2个簇或4个簇都是合理的,甚至,如果上面每一个圈的内部包含的是大量数据形成的数据集,那么也许分成16个簇才是所需要的。
论数据集应该聚类成多少个簇,通常是在讨论我们在什么尺度上关注这个数据集。层次聚类算法相比划分聚类算法的优点之一是可以在不同的尺度上(层次)展示数据集的聚类情况。
基于层次的聚类算法(Hierarchical Clustering)可以是凝聚的(Agglomerative)或者分裂的(Divisive),取决于层次的划分是“自底向上”还是“自顶向下”。
2.层次聚类流程
自底向上的合并算法
层次聚类的合并算法通过计算两类数据点间的相似性,对所有数据点中最为相似的两个数据点进行组合,并反复迭代这一过程。简单的说层次聚类的合并算法是通过计算每一个类别的数据点与所有数据点之间的距离来确定它们之间的相似性,距离越小,相似度越高。并将距离最近的两个数据点或类别进行组合,生成聚类树。
相似度的计算
层次聚类使用欧式距离来计算不同类别数据点间的距离(相似度)。
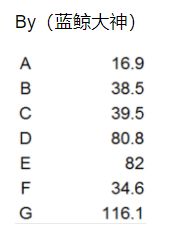
实例:数据点如下
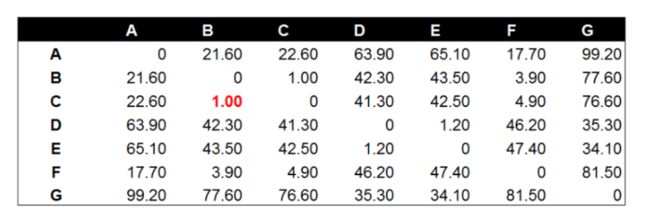
分别计算欧式距离值(矩阵):
数据点B与数据点C进行组合后,重新计算各类别数据点间的距离矩阵。数据点间的距离计算方式与之前的方法一样。这里需要说明的是组合数据点(B,C)与其他数据点间的计算方法。当我们计算(B,C)到A的距离时,需要分别计算B到A和C到A的距离均值。
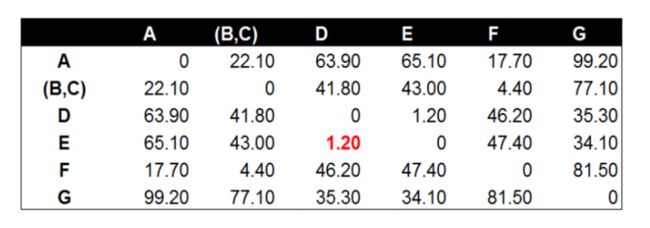
经过计算数据点D到数据点E的距离在所有的距离值中最小,为1.20。这表示在当前的所有数据点中(包含组合数据点),D和E的相似度最高。因此我们将数据点D和数据点E进行组合。并再次计算其他数据点间的距离。
后面的工作就是不断的重复计算数据点与数据点,数据点与组合数据点间的距离。这个步骤应该由程序来完成。这里由于数据量较小,我们手工计算并列出每一步的距离计算和数据点组合的结果。
两个组合数据点间的距离
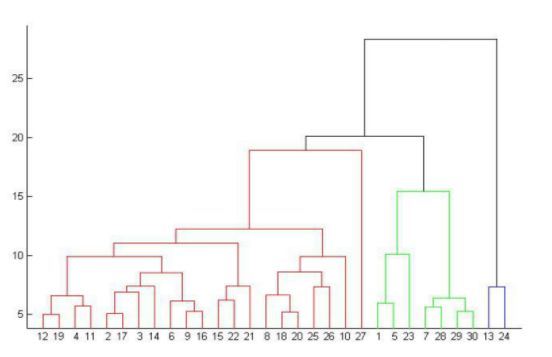
计算两个组合数据点间距离的方法有三种,分别为Single Linkage,Complete Linkage和Average Linkage。在开始计算之前,我们先来介绍下这三种计算方法以及各自的优缺点。
-
Single Linkage:方法是将两个组合数据点中距离最近的两个数据点间的距离作为这两个组合数据点的距离。这种方法容易受到极端值的影响。两个很相似的组合数据点可能由于其中的某个极端的数据点距离较近而组合在一起。
-
Complete Linkage:Complete Linkage的计算方法与Single Linkage相反,将两个组合数据点中距离最远的两个数据点间的距离作为这两个组合数据点的距离。Complete Linkage的问题也与Single Linkage相反,两个不相似的组合数据点可能由于其中的极端值距离较远而无法组合在一起。
-
Average Linkage:Average Linkage的计算方法是计算两个组合数据点中的每个数据点与其他所有数据点的距离。将所有距离的均值作为两个组合数据点间的距离。这种方法计算量比较大,但结果比前两种方法更合理。
我们使用Average Linkage计算组合数据点间的距离。下面是计算组合数据点(A,F)到(B,C)的距离,这里分别计算了(A,F)和(B,C)两两间距离的均值。
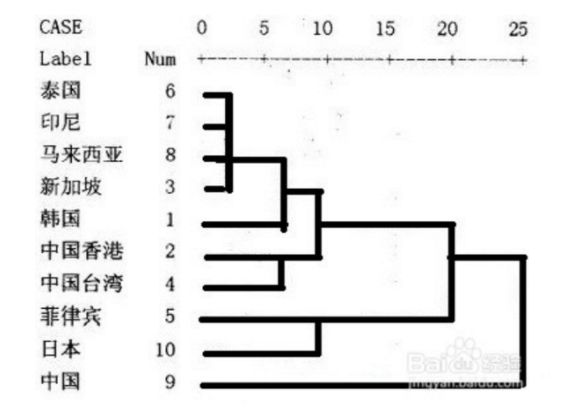
树状图
3.层次聚类实例
import pandas as pd
seeds_df = pd.read_csv('./datasets/seeds-less-rows.csv')
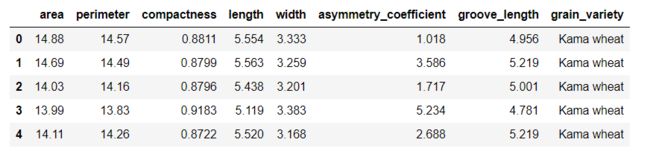
seeds_df.head()seeds_df.grain_variety.value_counts() varieties = list(seeds_df.pop('grain_variety'))
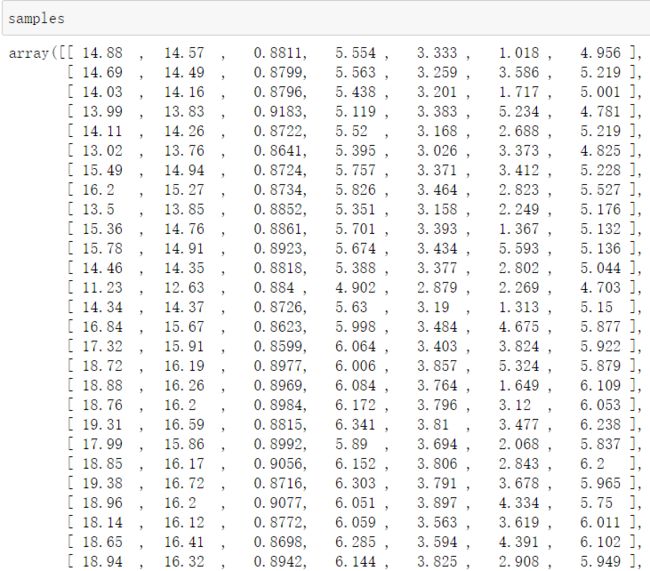
samples = seeds_df.values#距离计算的 还有树状图
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt#进行层次聚类
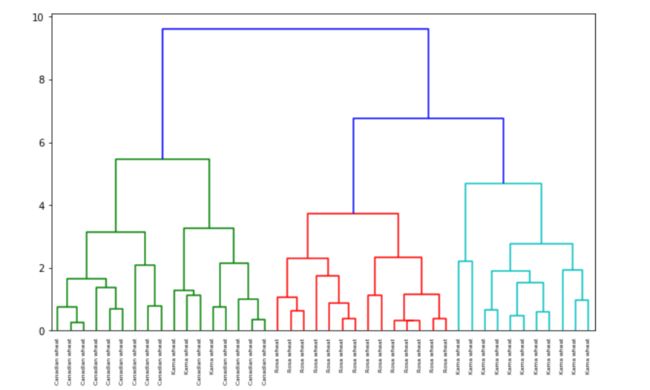
mergings = linkage(samples, method='complete')#树状图结果
fig = plt.figure(figsize=(10,6))
dendrogram(mergings,
labels=varieties,
leaf_rotation=90,
leaf_font_size=6,
)
plt.show()#得到标签结果
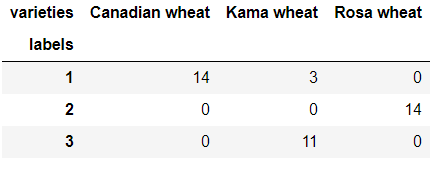
#maximum height自己指定
from scipy.cluster.hierarchy import fcluster
labels = fcluster(mergings, 6, criterion='distance')
df = pd.DataFrame({'labels': labels, 'varieties': varieties})
ct = pd.crosstab(df['labels'], df['varieties'])
ct不同距离的选择会产生不同的结果:
import pandas as pd
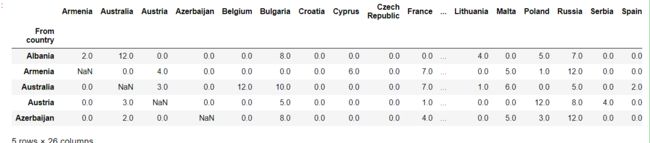
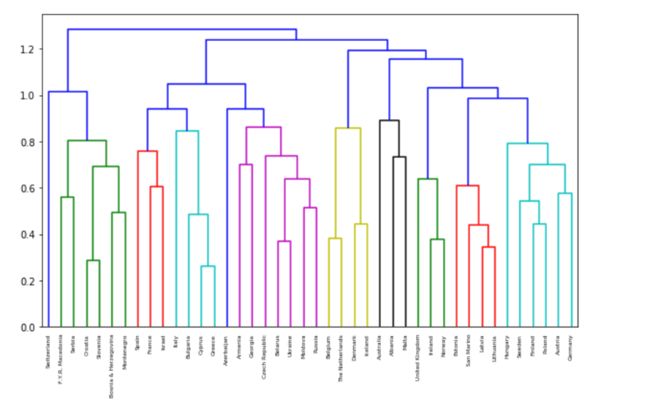
scores_df = pd.read_csv('./datasets/eurovision-2016-televoting.csv', index_col=0)
country_names = list(scores_df.index)
scores_df.head()#缺失值填充,没有的就先按满分算吧
scores_df = scores_df.fillna(12)
# 数据归一化
from sklearn.preprocessing import normalize
samples = normalize(scores_df.values)from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
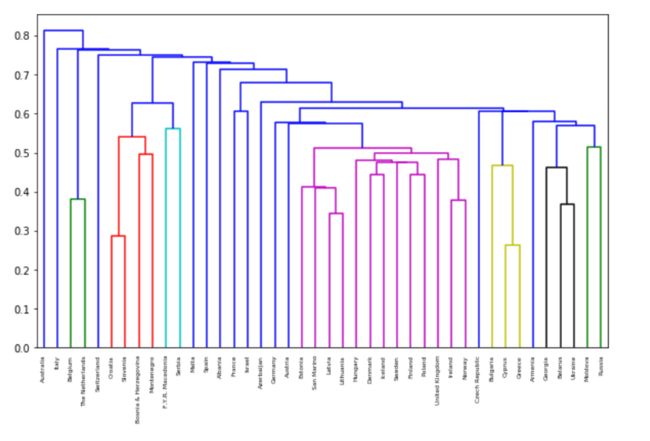
mergings = linkage(samples, method='single')
fig = plt.figure(figsize=(10,6))
dendrogram(mergings,
labels=country_names,
leaf_rotation=90,
leaf_font_size=6,
)
plt.show()mergings = linkage(samples, method='complete')
fig = plt.figure(figsize=(10,6))
dendrogram(mergings,
labels=country_names,
leaf_rotation=90,
leaf_font_size=6,
)
plt.show()3.KMeans算法概述
难点:如何评估,如何调参
要得到簇的个数,需要指定K值
质心:均值,即向量各维取平均即可
距离的度量:常用欧几里得距离和余弦相似度(先标准化)
工作流程:
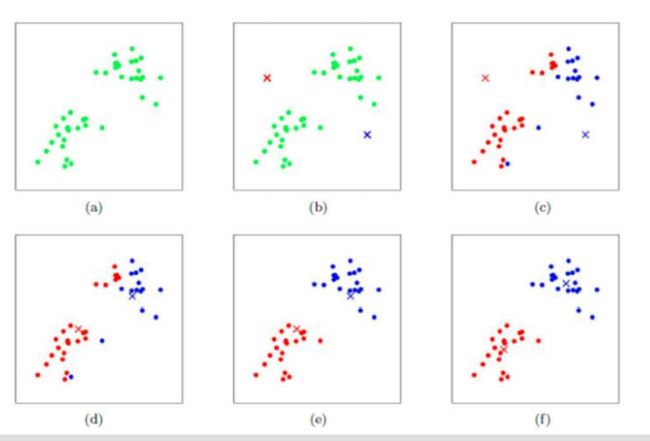
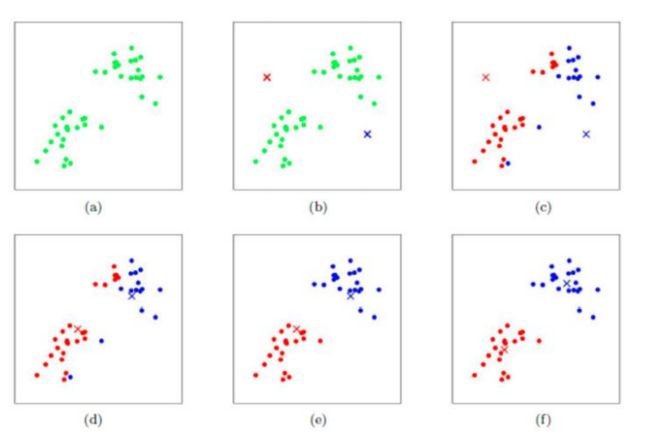
4.KMeans算法的工作流程
首先,我们指定K值,即分为多少类,在这个实例中,我们选取K值为2,然后随机的选取两个质心,计算出所有的点到质心的距离,根据距离聚类成两类,然后,我们再根据距离,对质心进行更新,反复迭代,直到这些点的类别基本保持不变
优势:简单,快速,适合常规数据集
5.DBSCN算法
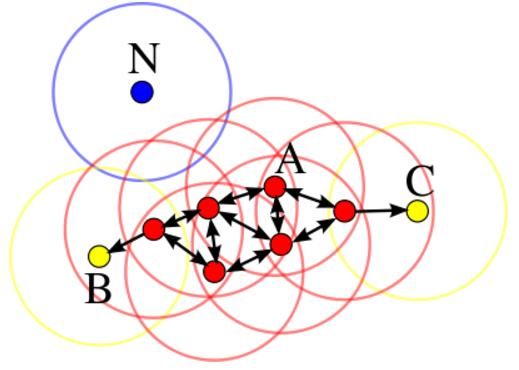
基本概念:(Density-Based Spatial Clustering of Applications with Noise)
A:核心对象 B,C:边界点 N:离群点
工作流程:
参数D:输入数据集
参数ϵ:指定半径
MinPts:密度阈值
参数选择: