计算机视觉算法——图像分割网络总结
计算机视觉算法——图像分割网络总结
- 计算机视觉算法——图像分割网络总结
-
- 1. FCN
-
- 1.1 关键知识点——网络结构及特点
- 1.2 关键知识点——转置卷积
- 1.3 关键知识点——语义分割评价指标
- 2. DeepLab
-
- 2.1 DeepLab V1
-
- 2.1.1 关键知识点——网络结构及特点
- 2.1.2 关键知识点——膨胀卷积
- 2.2 DeepLab V2
-
- 2.2.1 关键知识点——网络结构及特点
- 2.2.2 关键知识点——ASPP(Atrous Spatial Pyramid Pooling)
- 2.3 DeepLab V3
-
- 2.3.1 网络结构及特点
- 3. U-Net
-
- 3.1 关键知识点——网络结构及特点
计算机视觉算法——图像分割网络总结
我关注的B站Up主霹雳吧啦Wz又更新了图像分割相关的学习视频，之前跟着Up主已经学习了
计算机视觉算法——图像分类网络总结
计算机视觉算法——目标检测网络总结
两方面知识，图像分割同样也是计算机视觉中非常重要的的一部分，这篇博客就是跟着Up主学习的一个学习笔记，中间会补充一些我的个人理解，想要完整学习的读者建议还是跟着原视频学习一遍，会更有收获的。
1. FCN
FCN发表于2015年CVPR，论文全称为《Fully Convolutional Networks for Semantic Segmentation》是首个端对端的针对像素级预测的全卷积网络
1.1 关键知识点——网络结构及特点
FCN网络结构如下图所示，是通过将VGG16网络最后三层的全连接网络替换为全卷积网络，将网络最后的输出也由分类结果变化成一张热力图，而这张热力图通过上采样最终就能获得我们需要的分割结果：
具体的网络结构一共有三种，分别是FCN-32s、FCN-16s和FCN-8s，如下图所示，分别指的是选取不同的特征层分别进行32倍、16倍和8倍上采样得到：
在论文的实验结果中，由于FCN-8s融合（特征层相加）更多的特征信息，因此它的结果是最好的，如下图所示：
1.2 关键知识点——转置卷积
转置卷积是Transposed Convolution的直译，又可以称为fractionally-strided convolution或者deconvolution，FCN网络中上采样的部分就是使用的转置卷积。说先对于上采样，我们知道常见的有最近邻插值、双线性插值等，如下图就是双线性插值的结果：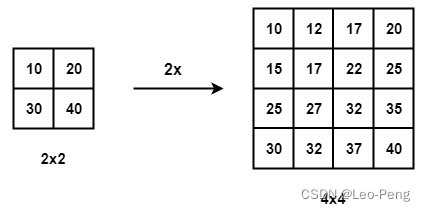
这样的插值方法是固定的，是不可学习的，而转置卷积也是卷积，其kernel是可以学习的，转置卷积的具体步骤如下：
（1）在输入特征图元素间填充 stride − 1 \text{stride}-1 stride−1行和列；
（2）在输入特征图四周填充 kernelsize − padding − 1 \text{kernelsize}-\text{padding}-1 kernelsize−padding−1行和列；
（3）将卷积核参数上下、左右翻转；
（4）做正常卷积运算；
经过转置卷积后特征图大小变为： H out = ( H in − 1 ) × stride [ 0 ] − 2 × padding [ 0 ] + kernelsize [ 0 ] W out = ( W in − 1 ) × stride[1] − 2 × padding [ 1 ] + kernelsize[1] \begin{aligned} H_{\text {out }} &=\left(H_{\text {in }}-1\right) \times \text { stride }[0]-2 \times \text { padding }[0]+\text { kernelsize }[0] \\ W_{\text {out }} &=\left(W_{\text {in }}-1\right) \times \text { stride[1] }-2 \times \text { padding }[1]+\text { kernelsize[1] } \end{aligned} Hout Wout =(Hin −1)× stride [0]−2× padding [0]+ kernelsize [0]=(Win −1)× stride[1] −2× padding [1]+ kernelsize[1] 如下图就是 stride = 2 ， kernelsize = 3 ， padding = 1 \text{stride}=2，\text{kernelsize}=3，\text{padding}=1 stride=2，kernelsize=3，padding=1的情况：
读者看到这里可能有两个问题：（1）为什么叫做转置卷积呢？（2）为什么要对卷积核参数进行上下、左右翻转呢？这里我们通过一个实际例子来分析，我们从普通的卷积过程开始，如下图所示
我们定义卷积符号为 ∗ * ∗，那么该过程可以写为：
我们将起写为等效矩阵的形式，即输出特征图各个元素都等于输入特征图与某个等效矩阵相乘的结果，而这个等效矩阵就是由卷积的Kernel平移和填充而来，我们用符号 × × ×表示这个过程，如下所示：
等效矩阵的方式又可以进一步通过矩阵的相乘的方式表达，其中符号 @ @ @表示矩阵乘法：
以上我们将一个 1 × 16 1×16 1×16维的矩阵通过与 16 × 4 16×4 16×4的矩阵相乘变成了 1 × 4 1×4 1×4维的矩阵，这个降维过程是不可逆的，但是我们可以通过将 1 × 4 1×4 1×4维的矩阵乘以 16 × 4 16×4 16×4的矩阵的转置得到一个新的 1 ∗ 16 1*16 1∗16的矩阵，如下所示：
该过程可以类似地转换为等效矩阵的方式表达：
最后我们再将等效矩阵的形式转化为卷积的形式，那么就得到了转置卷积的结果：
如下图所示：
从上面的流程中可以看到，对于同一个卷积核，如果是转置卷积就需要先对卷积核进行上下、左右翻转，然后再进行普通卷积，得到的才是正确的转置卷积的结果，而为什么称为转置卷积应该也和上述步骤中的转置过程有关，也进一步说明转置卷积并不是卷积的逆运算。
1.3 关键知识点——语义分割评价指标
这里介绍常见的三种语义分割评价指标，其中 n i j n_{ij} nij表示类别 i i i被预测成类别 j j j的像素个数， n c l s n_{cls} ncls表示目标类别个数（包含背景）， t i = ∑ j n i j t_{i}=\sum_{j} n_{i j} ti=∑jnij表示类别 i i i的总像素个数：
（1）Pixel Accuracy（Global Accuracy） ∑ i n i i ∑ i t i \frac{\sum_{i} n_{i i}}{\sum_{i} t_{i}} ∑iti∑inii表示的就是预测正确的像素和总像素个数的比。
（2）Mean Accuracy 1 n c l s ⋅ ∑ i n i i t i \frac{1}{n_{c l s}} \cdot \sum_{i} \frac{n_{i i}}{t_{i}} ncls1⋅i∑tinii表示的是每个类别预测正确的像素和属于该类别像素的比，最后再根据类别求平均的值。
（3）Mean IoU 1 n c l s ⋅ ∑ n i i t i + ∑ j n j i − n u \frac{1}{n_{c l s}} \cdot \sum \frac{n_{i i}}{t_{i}+\sum_{j} n_{j i}-n_{u}} ncls1⋅∑ti+∑jnji−nunii表示的是每个类别IoU，最后根据类别求平均的值。这里的IoU和目标检测中IoU定义基本上是一致的，就是目标检测结果与对应真值的面积交集比上面积并集。Mean IoU是在论文最常见的指标之一。
2. DeepLab
DeepLab一共有三个系列，分别是Deep Lab V1、V2、V3，下面分别介绍
2.1 DeepLab V1
DeepLab V1发表于2014年的CVPR，论文全称为《Semantic Image Segmentation with Deep Convolutional Nets and Fully Connnected CRFs》，论文引言中提出，将Deep Convolutional Neural Network用于语义分割任务上主要存在两个难点分别是Signal Sampling和Spatial Insensitivity，其中前者指的是网络的下采样部分会使得图像的分辨率降低，后者指的是空间不敏感的问题（语义分割是需要空间敏感的，对于同一物体的不同观察需要结果不同），针对这两个问题作者分别提出了膨胀卷积和Fully-Connected Conditional Random Field两个解决方案。
2.1.1 关键知识点——网络结构及特点
DeepLab V1网络结构和FCN其实差别不大，都是有VGG16网络改进升级而来，具体的网络结构我们在V2和V3时再做进一步介绍。
DeepLab V1网络的特点是：
（1）速度更快，主要是采用了空洞卷积原因，但是Fully-Connected Conditional Random Field仍然比较耗时；
（2）准确率更高，如下图所示：
在对比中Deep Lab的几个参数
CRF指的是Conditional Random Field模块，该模块在升级到DeepLab V3后就不再使用了，因此就不在此进行介绍。
MSc指的是Multi-Scale模块，将输入以及前四层最大池化后的特征层通过两层MLP和网络最后的输出特征concatenate到一起，该模块能稍微提高mean IoU指标，但是会增大网络参数数量，因此作者不建议使用，在此我们也不进行过多介绍。
LargeFOV模块其实指的就是对膨胀卷积的应用，前面说到，DeepLab网络和FCN网络一样同样是在VGG16网络上的基础上将最后三层全连接层转化为卷积层，作者指出者三层卷基层中的第一层原本使用的大小为 7 × 7 7\times7 7×7的4096个卷积核，但是这成为了网络计算的瓶颈，因此作者将该层更换为了大小为 4 × 4 4\times4 4×4的膨胀卷积，其作用是在不降低网络的mean IoU指标的前提下，降低网络的参数数量以及加快网络的训练速度，具体实现后文详解。
2.1.2 关键知识点——膨胀卷积
膨胀卷积又名空洞卷积，如下就是膨胀因子为2的膨胀卷积的示意图，其实就是卷积本身是带有空洞的：
其作用主要是可以：
（1） 增大感受野，所谓增大感受野我们可以通过感受野的计算公式实际计算下，感受野计算公式如下： r l = r l − 1 + ( k l − 1 ) × j l − 1 r_l = r_{l-1}+(k_l-1)\times j_{l-1} rl=rl−1+(kl−1)×jl−1其中 r l r_l rl为第 l l l层感受野， k l k_l kl为第 l l l层卷积大小， j l j_l jl为第 l l l层卷积步长，我们使步长为 1 1 1，大小为 3 × 3 3\times 3 3×3的普通卷积叠加三层，那么我们的感受野就是 7 × 7 7\times 7 7×7，如果我们使用同样补偿为 1 1 1，大小为 3 × 3 3\times 3 3×3，膨胀因子分别 1 、 2 、 3 1、2、3 1、2、3的膨胀卷积叠加三层，那么感受野就变成了 13 × 13 13\times 13 13×13，也就是实现了在相同参数下获得更大的感受野。
（2）保持原输入特征图大小，在语义分割网络中，为了增大感受野，我们通常会使用Max Pooling层对特征层进行下采样，这样就会导致特征的一些细节的丢失，如果不使用Max Pooling层，又会使得网络的感受野过小，而此时我们就可以使用膨胀卷积，在不使用Max Pooling层改变特征图大小前提下增加感受野。
在使用膨胀卷积中经常会遇到一个Gridding Effect的问题，如下图所示
上图中
（a）从左到右分别是使用 3 × 3 3 \times 3 3×3的卷积，膨胀因子固定为 2 2 2的三个卷积叠加使用后的对感受野的影响，从结果看会发现这样的卷积对感受野的影响并不是连续的，而是仅仅利用到中间一部分像素。
（b）同样是三个 3 × 3 3\times3 3×3卷积，但是膨胀因此依次是 1 、 2 、 3 1、2、3 1、2、3，这种情况下感受野和第一种情况是相同的，但是其使用到了感受野中所有的像素。
在《Understanding Convolution for Semantic Segmentation》一文中提出了“卷积中两个非零元素的最大距离计算公式”、“膨胀系数设置为锯齿状分布”，“膨胀系数公约数不能大于一”等一系列避免Gridding Effect的建议，这里感兴趣的读者可以去看下论文，在此不再赘述。
2.2 DeepLab V2
2.2.1 关键知识点——网络结构及特点
DeepLab V2提出于2016年CVPR，论文全称为《DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs》，在论文引言中作者同样提出了将DCNN应用于语义分割任务的问题以及解决方案：
（1）分辨率被降低：将最后几个Max Pooling层的stride设置成1（分辨率不变），配合使用膨胀卷积；
（2）目标的多尺度问题：将图像缩放到多个尺度分别通过网络进行推荐，然后将多个结果进行融合，这样做计算量较大，为了解决该问题，DeepLab V2提出了ASPP模块；
（3）DCNN的不变形会降低定位精度：和DeepLab V1类似通过CRFs解决，不过DeepLab V1是使用的是Fully Connected Pairwise CRF，相对于DeepLab V1中的Fully Connected CRF更高效；
DeepLab V2的网络除了以上优化方法外，还将BackBone更换为了ResNet，综上网络特点主要是
（1）速度更快；
（2）准确率更高；
（3）模型结构简单，通过DCNN与CRF联级；
2.2.2 关键知识点——ASPP(Atrous Spatial Pyramid Pooling)
ASPP模块结构如下：
简单而言，就是类似于Google Net将网络的Feature Map同时送入不同的分支进行卷积，然后再将卷积后的结果进行Concatenate，这里不同分支之间的区别主要是膨胀卷积的膨胀系数不同，在DeepLab V2中一共提出了两种配置，分别是ASPP-S（膨胀系数分别是2，4，6，8）以及ASPP-L（膨胀系数分别是6，12，18，24），他们的结果对比如下：
可以看到，ASPP-L相对于单通道的LargeFOV还是有较大提升的，具体的LargeFOV结构和ASPP结构对比如下：
2.3 DeepLab V3
2.3.1 网络结构及特点
DeepLab V3发表于2017年的CVPR，网络原论文名为《Rethinking Atrous Convolution for Semantic Image Segmentation》，相对于DeepLab V2主要的不同点是
（1）引入了Multi-Grid结构；
（2）改进了ASPP结构；
（3）移除了CRFs后处理模块；
在论文中，作者提出了获得多尺度信息的四种方式如下图所示，
其中第一种就是将训练数据进行上下采样；第二种就是采用类似于U-Net的网络结构；第三种是通过膨胀卷积进行级联，也就是本文提出的Cascaded Model；第四种是采用ASPP 模块，也就是本文提出的ASPP Model；
Cascaded Model结构如下图所示：
其中Block1-Block3位原始ResNet网络中的结构，而Block4-Blcok7与ResNet的Block结构相同，但是卷积均为膨胀卷积，每一层的膨胀系数还不一样，这就是Multi-Grid结构，我们还注意到图中由rate这个参数，这里的rate与每一层膨胀卷积的膨胀系数相乘后的值才是该卷积层最后的膨胀系数，我们可以看到在Block4-Blcok7中rate是2，4，6，16依次递增的。
ASPP Model结构如下图所示：
相对于DeepLab V2中的ASPP模块，这里的ASPP模块中还添加了一个全局池化的通道（Image Pooling），除此之外，后面还添加了 1 × 1 1\times1 1×1的卷积层（包括BN层和ReLU层）进行进一步的融合。
3. U-Net
UNet发表于2015年的MICCAI，原论文名为《U-Net: Convolutional Networks for Biomedical Image Segmentation》，UNet主要应用与医学影像领域，在我之前接触到的降噪算法中，U-Net也是一个非常有效的结构。
3.1 关键知识点——网络结构及特点
UNet网络结构如下图所示：
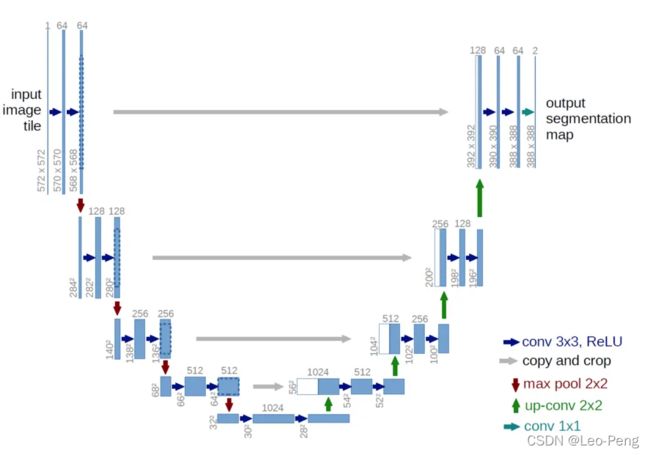
U-Net的网络结构是清晰明了的，我们注意一下几点：
（1）U-Net主要由两部分构成，下采样的部分作用主要是提取特征，原论文称为contracting path，上采样的部分主要作用是回复尺寸和特征融合，原论文称为expensive path；
（2）在原始的U-Net中，作者为了减小计算量有一个crop操作，导致最终网络输出的分割结果和原图大小不一致，而目前主流的实现方式是不进行crop操作的；
（3）这里上采样都是通过转置卷积实现的，转置卷积的原理参看FPN章节的介绍；