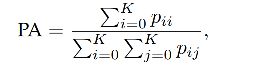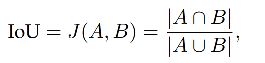【语义分割】语义分割综述

一、分割方法介绍

图像分割是机器视觉任务的一个重要基础任务，在图像分析、自动驾驶、视频监控等方面都有很重要的作用。图像分割可以被看出一个分类任务，需要给每个像素进行分类，所以就比图像分类任务更加复杂。此处主要介绍 DL-based 方法。

mmsegmentation 分割网络结构通用模式：

• encoder：输入图像→resize到特定大小→输入 backbone→得到特征图

• 可选：decode_head[0]：特征图→FCN→类别特征图→求带权重的 loss（权重0.4）

• 可选：decode_head[1]：特征图→特定解码头（psp/ocr等）→类别特征图→求带权重的 loss（权重1.0）

分割主要面临的问题及对应的已有解决方案：

• 速度和内存限制，需要降低分辨率，缺失了大量细节信息：多级特征融合、膨胀卷积扩大感受野
• 上采样方式导致的信息丢失：Deconvolution Network ，encoder-decoder 网络，通过优化 decoder 网络来提高对细节特征的定位能力
• 卷积只能考虑局部信息，丢失了全局信息：attention
• 目标大小相差较大：多尺度融合、多膨胀率卷积并融合特征

参考文献：

[1] Image Segmentation Using Deep Learning: A Survey
[2] A survey of loss functions for semantic segmentation

1.1 Fully Convolutional Networks [2015]

1.1.1 FCN

论文：Fully convolutional networks for semantic segmentation

语义分割可以看做一个分类模型，唯一复杂的地方在于需要给图像中的每个像素进行分类。

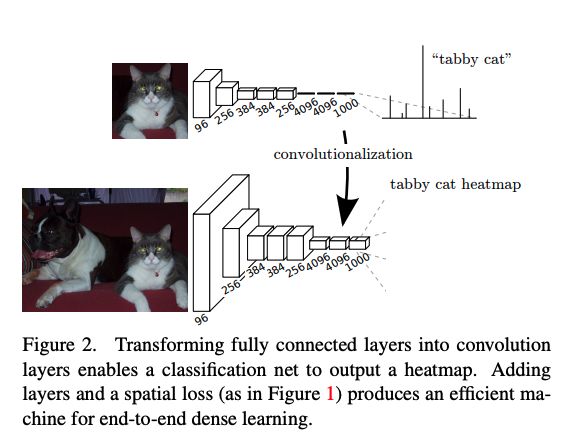
分类模型一般都是接受相同大小的输入图像，摒弃空间坐标。其使用的全连接层可以被看成一个核能够覆盖全部元素的卷积层。

所以，是否能使用全卷积网络来替代全连接网络呢？

答案是可以的，使用全卷积网络还避免了必须使用“相同大小的输入”的需求，两个网络的转换如图 2 所示。

FCN 方法是第一个基于深度学习的分割方法，只包含卷积层，可以输入任意大小的图然后生成其分割结果图。

如何从分类任务到 dense FCN：

backbone：VGG-16（和 VGG-19 的效果类似）或 GoogLeNet（使用最后的 loss 层）

使用 backbone 的方式：去掉最后一层分类层，使用 1x1 卷积将通道数变成分割的类别数（PASCAL 中使用 21，其中一类为背景），然后使用 deconvolution 层上采样。

将类别和位置进行结合：

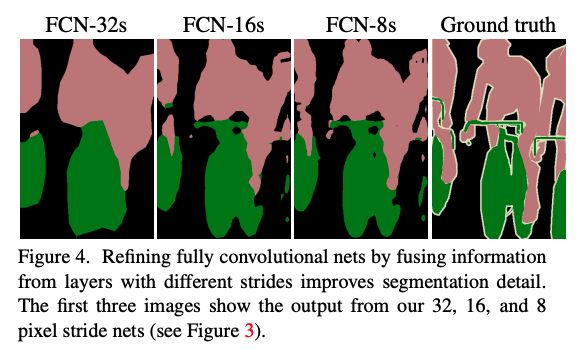
如图 3 所示，作者采用将层级特征进行结合的方式来精细化分割任务在空间上的类别预测。

详解：

• FCN-32s：直接将 pool5 的输出，上采样到原图大小，做预测，从图 4 可以看出，预测的结果非常粗糙（mIoU 59.4）
• FCN-16s：将 pool5 上采样 2 倍，和 pool 4 特征进行相加，然后上采样到原图大小，结果会比 32s 的精细一些（mIoU 62.4）
• FCN-8s：将 pool5（上采样2倍）和 pool4 相加后的特征，先上采样 2 倍，然后和 pool3 相加，得到 FCN-8s 特征（mIoU 62.7）

从图 4 也能看出，将浅层特征和深层特征进行结合之后，能够让网络将全局和局部的特征进行结合，用全局的特征来指导局部特征的预测。

贡献：该方法是图像分割的一个重要的转折点，证明了深度学习网络可以端到端的实现对不同大小图像的语义分割。

缺点：FCN 模型速度较慢，无法支持实时的语义分割；没有考虑全局上下文信息；无法方便的扩展到 3D 图像。

1.1.2 ParseNet

论文：Parsenet: Looking wider to see better

FCN 为使用卷积网络来实现端到端的语义分割提供了很好的思考方式，但却忽略了很重要的全局上下文信息，但在 FCN 中添加全局上下文信息也很容易，所以 ParseNet 使用平均特征来加强特征，并且这种特征为语义分割带来了很好的提升。

ParseNet 贡献点：

使用全局上下文信息来来解决局部误识别问题，且引入的计算量非常小，和标准 FCN 基本一致。

① 添加全局特征的方式：parsenet 使用早融合的方式

• 早融合方式：

如图 1e 所示，unpool（也就是重复的扩大）全局特征到和原特征相同大小，然后 concat 起来，一起去学习分类结果。

• 晚融合方式：

全局特征和原特征都分别学习分类，然后将两个预测的分类结果结合起来，作为最终的分类结果。

如果忽略结合特征后的训练过程，则两种融合方式的结果差不多，但是在某种特征辅助下的局部特征才能判断出正确的分类结果，所以，如果先训练再整合则造成的损失是不可逆的。

② 为什么要归一化

如图 3 所示，当要结合两组特征时，如果两者的 scale 和 norm 相差很大的话，则大的一方容易吞掉小的一方，如果使用归一化，则能较好的避免该问题，且训练更稳定。

1.2 Encoder-Decoder Based Models

还有很多图像分割是基于卷积 encoder-decoder 结构的，可以分为两个大类：通用分割、医学图像分割

1.2.1 通用分割

1.2.1.1 Deconvolutional semantic segmentation

论文：Deconvolutional semantic segmentation

FCN 有两点不足的地方：

• FCN 网络只能处理单个尺度，因为其感受野是固定的，所以比该感受野大很多或者小很多的目标，就会出现一些误识别（包括分裂化和类别错误）。也就是说其 label 的预测仅仅基于局部信息，如此一来，就会出现：

  大目标：和其他类别的相似像素的类别错误，如下图 1a 所示
  小目标：被误分类为背景像素，如下图 1b 所示

• 输入解卷积层的 label map 中，目标的细节结构被丢失或平滑掉了，且恢复大小的手段也很简单。FCN 中，label map 仅仅为 16x16 大小，然后使用双线性插值来复原并生成分割结果图。
  
  因此，本文的作者提出了 deconvolutional 语义分割网络：

• encoder 使用 VGG-16 中的卷积层

• decoder 使用反卷积层来生成分割图，反卷积层是由 deconvolution、 unpooling 和 ReLU 组成的。

Deconvolutional semantic segmentation 的框架结构：

如图 2 所示，框架主要由两部分组成：convolution 和 deconvolution

• convolution：特征提取和编码，本文使用 VGG-16 来实现，移除了后面的分类层，
• deconvolution：map 生成，最终的输出是和输入图像同等大小的概率 map，表示了每个像素属于对应类别的概率。

① Deconvolution Network for Segmentation

• Unpooling

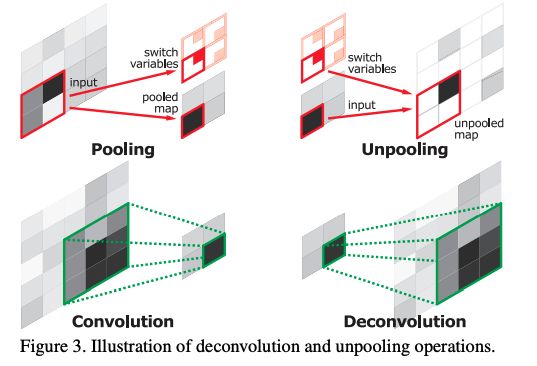
  卷积网络中的 pooling 能够增加感受野，降低计算量，但也会丢失位置信息，但语义分割中的位置信息还是很重要的。为了解决该问题，作者使用了 pooling 的反操作，并且将特征图复原到 pooling 之前的大小，如图 3 所示。在 pooling 的过程中，会记录最大值的来源未知，unpooling 的时候会再把 pooling 结果放到对应的位置上去。

• Deconvolution

  unpooling 操作是一个扩大后的稀疏 map，deconvolution 才做能够将该稀疏 map 稠密化。
  deconvolution 是 convolution 的反向操作，能够将单个输入扩展成多个输出，如图 3 所示，所以 deconvolution 的输出是一个扩大且稠密的特征图。
  deconvolution 的层级结构能够捕捉不同尺度的特征，低层捕捉目标的大体轮廓，高层捕捉类别精细特征。

② Deconvolution 网络分析：

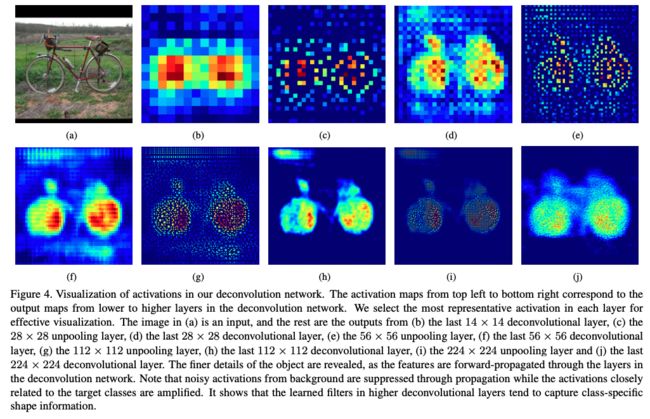
下图 4 可视化了网络的输出，可以看出，deconvolution 能够从粗到细提取目标的特征，unpooling 层通过追踪最强响应的位置来捕捉 example-specific 结构，能够高效的重建目标的细节信息。deconvolution 层能够捕捉 class-specific 形状，经过 deconvolution 后，与目标密切相关的激活特征被放大，而其他区域的噪声被抑制。这两者的结合能更有利于准确的 maps 的生成。

图 5 也展示了不同网络的输出效果，和 FCN-8s 相比，本文的网络结构预测更为精准

1.2.1.2 SegNet

论文：SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation

语义分割是像素级的分类任务，也出现了很多方法能够实现端到端的预测，直接得到每个像素的预测类别，但其结果大都比较粗糙。其问题主要是由 max-pooling 和 下采样导致丢失了一些信息。

作者为了将具有全局信息的低分辨率特征图更好的映射到输入大小的分辨率，这种映射需要很好的保留边界的位置信息。

所以本文构建了 SegNet，来实现高效且精细的语义分割。

关键点：

• SegNet 在解码器中使用去池化对特征图进行上采样，并在分割中保持高频细节的完整性。
• 编码器不使用全连接层（和 FCN 一样进行卷积），因此是拥有较少参数的轻量级网络。

结构：

• Encoder：VGG-16 网络（去掉最后一层分类层），共 13 层卷积层，

  卷积结构为 Conv+BN+ReLU，下采样使用最大池化来实现（2x2，s=2），但一般会丢失位置信息，逐级增加的损耗（boundary detail）非常不利于语义分割的结果
  语义分割中边界非常重要，所以，encoder 中尽可能多的保留边界信息非常重要。考虑到内存和效率问题，有一些方法提出保留最大值对应的位置来保留位置信息，所以本文也使用了这种方法。

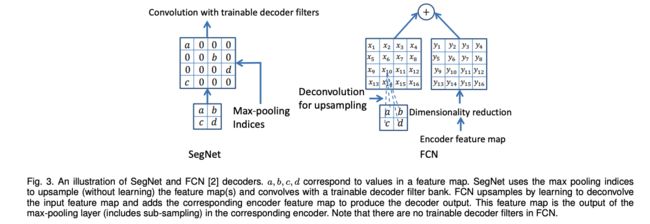
• Decoder：每个 encoder 都会对应一个 decoder，所以 decoder 也共有 13 层，通过使用 memorized max-pooling 的方式，来上采样。解码的结构如图 3 所示，

• 分类层：最后一层 decoder 的输出会输入 multi-class soft-max 分类器，为每个像素来生成对应的类别预测

1.2.1.3 HRNet

Original HRNet 论文：Deep High-Resolution Representation Learning for Human Pose Estimation
HRNetV2 论文：High-Resolution Representations for Labeling Pixels and Regions

HRNet 通过将由高到低的分辨率特征结合起来的方式，实现对高分辨率特征的保留，并且不同分辨率的特征也进行了信息交换。所以有很多分割的方式使用 HRNet 作为 backbone，来为模型中引入上下文信息的开拓能力。

深度学习中有高层特征也有低层特征，有很多研究都证明了，低分辨率的高级特征适合于分类任务，高分辨率的低级特征对密集预测有重要意义，如姿态估计、目标检测、语义分割等。

最开始提出的 Original HRNet 仅仅使用了 high-resolution 的特征表达，如图所示，本文对 Original HRNet 做了一些修改，并行使用了 high-to-low resolution 的特征表达，也叫 HRNetV2。

Original HRNet：

HRNetV2：

这里展示一组 HRNetV2 输出的分辨率：

• [2, 18, 128, 256]
• [2, 36, 64, 128]
• [2, 72, 32, 64]
• [2, 144, 16, 32]

分割如何使用这组多分辨率特征：上采样到相同大小，也就是最大的特征图大小，然后 concat，最后得到如下大小，再送入 decode_head 来使用：

• [2, 270, 128, 256]

HRNetV2 结构：

如上图 1 所示，总共有 4 stages，每个stage结构类似，都是 multi-resolution block，都是高分辨率特征和低分辨率特征的结合。

第一个 stage 的输入：原图经过两层 3x3 的卷积进行特征提取后的图（1/4原图大小）

multi-resolution block 主要包括两个模块：

• 多分辨率特征分组卷积模块：multi-resolution group convolution（图2a）
• 多分辨率特征卷积模块：multi-resolution convolution（图2b）

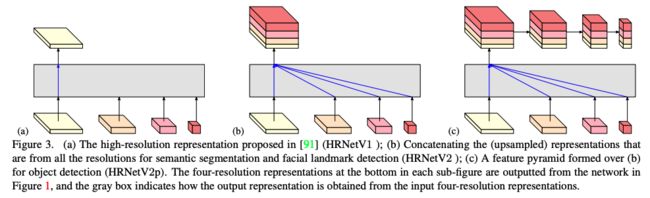
HRNet 的对比：

• HRNetV1：如图 3a 所示，只使用了分辨率最大的分支的输出，也就是会丢失掉其他从高分辨率分支抽取到的特征及其他低分辨率的特征。
• HRNetV2：如图 3b 所示，将低分辨率的输出上采样，和最高分辨率的输出 concat，一般用于语义map或面部关键点识别。
• HRNetV2p：如图 3c 所示，将 HRNetV2 的输出结果，使用平均池化进行下采样，得到多尺度特征，用于目标检测。

下图也通过定量分析，验证了 HRNetV2 和 HRNetv2p 确实优于 HRNetV1。

1.2.2 医学图像分割

1.2.2.1 U-Net [2015]

论文：U-net: Convolutional vnetworks for biomedical image segmentation

训练深度学习网络需要大量的数据，语义分割的难点在于：高分辨率特征和低分辨率特征的结合，也可以看做是低层位置信息和高层语义信息的结合，缺一不可，所以两者如何联合使用是一个很值得研究的问题

• 高分辨率特征能够保证位置信息
• 低分辨率特征能够保证语义信息

本文在 FCN 的基础上，进行了一些修改和优化，能够保证在使用少量数据的基础上产生更准确的分割结果。

FCN 的主要核心:

• 在常规的卷积层后，添加了上采样层，将特征图扩大，并且在扩大的时候使用了前一层的高分辨率特征，引入了更优质的位置信息。

U-Net 的主要改进在于：

• 在上采样部分，也采用了很多的通道，能让更多的上下文信息传递到高分辨率层
• 使用了一些数据增强方法，让网络能够学习更鲁棒的特征
• 使用了加权 loss

U-Net 框架结构：

如图 1 所示，U-Net 和 FCN 结构类似，也分为 encoder 和 decoder 模块，网络结构中只有卷积和池化层，包括两个路径：

• 捕获上下文信息的收缩路径（encoder）
• 实现精确定位的对称扩展路径（decoder）

特点：

• U-Net 的上下采样使用了相同数据的卷积操作，且使用了 skip 链接，使得下采样层的特征直接传递到上采样层，保证了 U-Net 更精确的像素定位。
• U-Net 训练效率也高于 FCN ，U-Net 只需要一次训练，而 FCN-8s 需要 3 次训练

1.2.2.2 V-Net [2016]

论文：V-net: Fully convolutional neural networks for volumetric medical image segmentation

1.3 Multi-Scale and Pyramid Network Based Models

1.3.1 FPN [2017]

论文：Feature Pyramid Networks for Object Detection

FPN 最初被提出的时候是被用于目标检测的，目标检测任务中的目标大小不一，尺度相差也比较大，但由于计算量和内存的原因，特征金字塔在很长一段时间并没有被广泛使用。所以本文的作者就提出了 FPN 模块，可以嵌入任何网络结构（如 Faster R-CNN 等），并且计算开销很小。

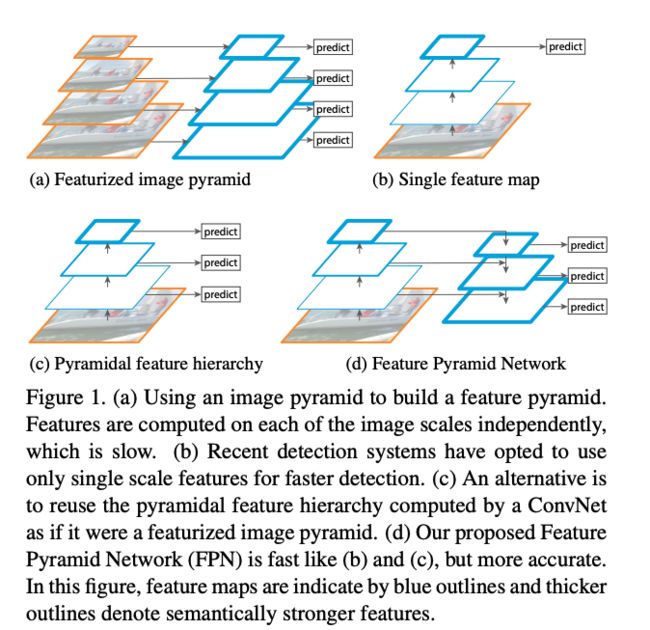
结构：

• 图 1a 是基础的图像金字塔结构，对原图做 resize，然后分别提取特征，分别做预测
• 图 1b 是单个尺度的金字塔，只使用最后一层的特征来做预测
• 图 1c 是使用多层的特征分别做预测
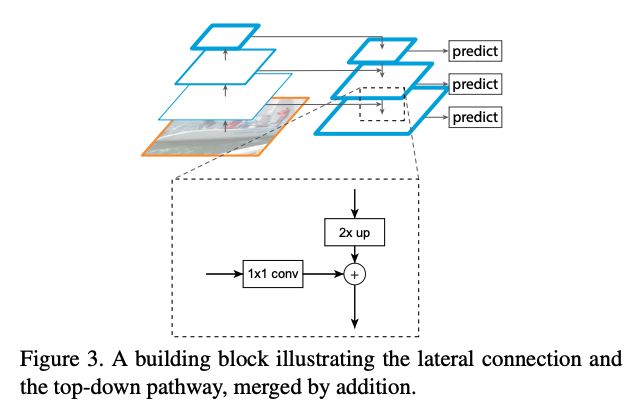
• 图 1d（FPN 的结构）是会对不同尺度的特征进行融合，再分别做预测，后一层的特征会通过上采样来和前一层的特征进行融合，即单层特征融合了其他层的特征。也可以理解为浅层融合了深层语义特征。

FPN 的特点：晚融合

也就是在每层和上层融合后，分别进行结果预测，然后再把结果进行融合

具体细节：

之后也被用于分割任务。FPN 能在只增加很少计算量的情况下，融合多尺度金字塔特征。之后，使用两个多层 MLP 来生成分割 mask。

1.3.2 PSPNet [2017]

论文：Pyramid Scene Parsing Network

Pyramid Scene Parsing Network（PSPNet），也是一个多尺度网络，能更好的学习全局上下文信息。

Scene Parsing 是基于语义分割的，也是计算机视觉的基础，需要给每个像素分配其类别。其难点在于场景和类别的多样性。

下图 2 的第一行展示了一种误识别：将船识别为了车

这种误识别可能是由于船和车的目标具有一定的相似性，但作者考虑，如果模型能考虑该目标（船）的上下文信息，则会发现船一般会和河流离得近，也许会降低误识别。

主要贡献：

提出了pyramid pooling module (PPM) 模块，聚合不同区域的上下文信息，从而提高获取全局信息的能力。

现有的深度网络方法中，某一个操作的感受野直接决定了这个操作可以获得多少上下文信息，所以提升感受野可以为网络引入更多的上下文信息。

框架：

Step1： 使用global averag pooling得到不同尺度的特征，PPM模块融合了4个不同尺度的特征：

• 红色是最粗糙尺度，使用一个global average pooling 实现
• 其他的都是将特征图切分为不同数量的块，在每个块内使用global average pooling （文中四个尺度分别是 1x1, 2x2, 3x3, 6x6）

Step2： global average pooling 之后，每层都接一个1x1的卷积来降低通道维度。

Step3： 上采样到和原图相同的尺寸，然后和进入PPM头之前的feature map 进行concat 来预测结果。

1.4 R-CNN Based Models(for Instance Segmentation)

Mask-RCNN 可以实现 object instance segmentation，在 COCO 数据集上取得了很好的成绩。

还有很多基于 Mask-RCNN 的实例分割结构。如 R-FCN、DeepMask、PolarMask、CenterMask 等。

1.5 Dilated Convolutional Models and DeepLab Family

膨胀卷积（Dilated，也叫 atrous 卷积）为卷积网络引入了一个新的参数——膨胀率。膨胀卷积能够在不引入额外参数的情况下，提高感受野，所以有很多实时的分割网络都会使用膨胀卷积。如 DeepLab 家族[78]、multi-scale context aggregation[79]、dense upsampling convolution and hybrid dilatedconvolution(DUC-HDC)[78]、densely connnected atrous spatial pyramid pooling(ASPP)[81] 和 efficient neural network(ENet)[82]。

1.5.1 Deeplab v1

论文：Semantic image segmentation with deep convolutional nets and fully connected crfs

本文认为语义分割的主要问题：

• 持续的下采样
• 空间位移不变性

本文的方法：

• 引入了膨胀卷积来扩大感受野
• 引入了 fully-connected CRF 来定位更精确的分割边界
  
  

1.5.2 Deeplab v2

论文：Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs

本文认为语义分割的主要问题：

• 为了分辨率下降而重复使用池化和下采样，丢失了位置等细节信息
• 目标尺度的多样性
• 空间位移的不变性（所以本文引入了 fully-connected CRF，为网络带来捕捉位置细节的能力）

Deeplab v2 有三个关键点：

• 使用膨胀卷积来降低网络中特征图的分辨率
• 提出了 ASPP，能够使用不同采样尺度的滤波器来提取卷积层的特征，捕捉不同尺度下的图像上下文信息
• 通过结合深度 CNN 和概率图（CRF）模型，提升了目标边界的定位能力

ASPP 框架结构： 4 组并行且使用不同膨胀率的卷积

1.5.3 Deeplab v3

论文：Rethinking atrous convolution for semantic image segmentation

改进：

• 改进了 ASPP（膨胀卷积后添加了 BN；增加了全局平均池化来引入全局信息）
• 去掉了 V2 的 CRF

本文认为语义分割的主要问题（Deeplab 系列提出的问题基本一样）：

• 降低分辨率以减少计算量，一般使用池化和步长卷积来实现，但这样会丢失较多的空间细节信息，所以使用膨胀卷积很有必要
• 目标大小差别较大，一般的解决方法为如下四种：多尺度融合、encoder-decoder 结构、使用额外的结构来捕捉长距离依赖、空间金字塔池化（多个不同的池化率，捕捉不同尺度的特征）

DeeplabV3 的解决方法：膨胀卷积（多种膨胀率）+ SPP

• 组合了级联和并联的膨胀卷积
• 并联的卷积模块被嵌入了 ASPP

语义分割的高级语义特征是需要从深层的低分辨率特征图中提取的，对比了使用和不使用膨胀卷积的情况：

• 不使用膨胀卷积：丢失了细节信息
• 使用膨胀卷积：分辨率保持

对 ASPP 的修改：

• 在 ASPP 中添加了 batch normalization，来加速训练，提升效果
• 增加了一个并行的全局平均池化，来捕捉全局信息

使用全局平均池化的原因：

ASPP 是使用不同的膨胀率来捕捉不同尺度的信息，但是当膨胀率变大的时候，有效的元素就越少，也就是间隔越大，会有很多权重落到特征图外，无法起作用，极端情况就是这个3x3的卷积的效果类似于一个1x1的卷积。

解决方式：

在最后一层特征图使用全局平均池化，将该 “image-level” 的特征输入 1x1 卷积中+BN 中，再上采样到需要的大小

修改后的 ASPP 如下图 5 所示，有两个部分：

• 原始 ASPP（1 个 1x1 卷积，3 个不同膨胀率的 3x3 卷积）
• 新加的全局平均池化
  

1.5.4 Deeplabv3+

论文：Encoder-decoder with atrous separable convolution for semantic image segmentation

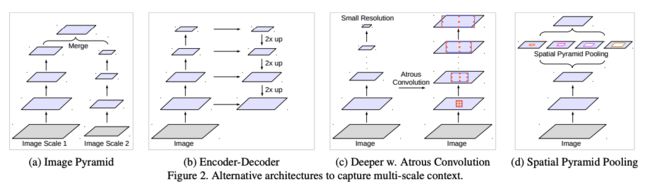
语义分割中的两个常用策略：

• 空间金字塔池化：捕捉多尺度上下文信息，提高感受野
• Encoder-decoder 框架：通过逐步恢复空间信息，来捕捉突变的边界信息

Deeplabv3+：将这个两个策略结合起来

Deeplabv3+ 和 Deeplabv3 的联系：

• Deeplabv3+ 将 Deeplabv3 作为 encoder
• 引入了 decoder 结构，来细化分割的结果

改进的动机：

• Deeplabv3 虽然通过使用改进的 ASPP 提升了分割的效果，也就是在最后一层特征图中，编码了丰富的语义信息，但目标的细节边界信息还是有很多的丢失（backbone 中的下采样和 stride 卷积等导致，还有效率和计算量的限制原因）
• encoder-decoder 框架由于 encoder 中舍弃了很多特征，所以计算很快，本文就提升了 encoder 的特征提取能力，促进 decoder 中更多信息的恢复。

框架结构：

• Encoder：使用 ASPP 来进行多尺度特征的提取，并concat，经过 1x1 卷积得到 16x 下采样的特征图，这个特征图编码了多尺度高级语义信息
• Decoder：使用高尺度语义信息（上采样到4x），和低层特征concat起来，经过卷积和上采样，得到最终解码的结果

1.6 Attention-based Models

1.6.1 Non-Local [2018]

论文：Non-Local Neural Networks

卷积网络是提取 local 特征的网络结构，为了捕捉长距离的依赖关系，作者提出了 non-local 的方法。可以和现有的结构结合，用于分类、目标检测、分割、姿态估计等。

non-local 的核心思想是计算特征图中的每个点和其他点的相关关系，也就是空间上的注意力。

1.6.2 PSANet

论文：PSANet: Point-wise Spatial Attention Network for Scene Parsing

上下文信息聚合的来提升感受野的操作，在 ParseNet、ASPP、PPM 等都有用到。

PSANet 中，作者提出了 point-wise spatial attention，来自适应的聚合长距离上下文信息。

1.6.3 OCNet

论文：Ocnet: Object context network for scene parsing

1.6.4 DANet [2019]

论文：Dual attention network for scene segmentation

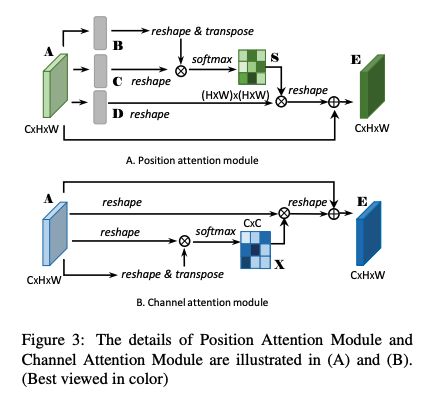
为了同时捕捉空间和通道的相关性，DANet 使用并行的方法，在通道和空间同时使用了 non-local 模块。两个模块如图 3 所示。

• position attention：也是空间 attention，可以得到每个像素和其他像素的关系，关系越近，权重越大
• channel attention：也是类别 attention，可以得到每个通道的权重，通道越重要，权重越大

1.6.5 OCRNet

论文：Object-Context Representations for Semantic Segmentation

动机：

语义分割任务中，每个像素的类别是该像素所属目标的类别，所以作者提出了和目标本身类别相关的方法，来给每个像素分配类别。

方法（以 cityscapes 为例）：这里最终的加权可以看做是像素和类别之间的加权

• 首先，得到普通的初始分割结果（19类）
• 然后，计算每个特征图（512）和初始分割结果（19）的相关性，得到 512x19 的矩阵
• 之后，用该 512x19 的矩阵，对特征图（512）加权，得到加权后的特征图
• 最后，对加权后的特征图进行特征抽取，得到加权后的最终分割结果（19类）

语义分割研究的一个重要分支就是抽取某个位置周边的上下文语义信息：

• 如 ASPP 和 PPM 都捕捉了多尺度的上下文语义信息。OCRNet 和 ASPP 的不同可以见下图 2。ASPP 只能抽取多尺度的上下文信息，而 OCR 可以将不属于同一个类别的像素区分开，让它们离得更远。
• DANet、CFNet、OCNet，都考虑了某个位置和其上下文位置的信息，并且对该位置周边的位置的上下文赋予了更高的权重。

下面对比了 DANet 和 OCR 的特征图对比，可以看出 OCR 的单个特征图会聚焦于某个特定类别，DANet 的特征图中类别的信息不明确。

1.7 Transformer-based Segmentation

1.7.1 SETR

论文： Rethinking semantic segmentation from a sequence-to-sequence perspective with transformers

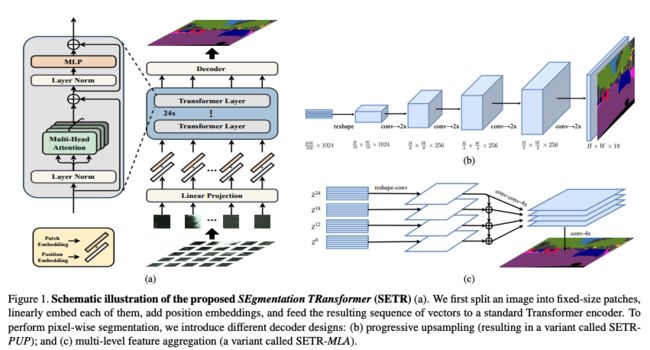
SETR 是首个在分割任务上超越 CNN 的 Transformer 网络结构，该论文作者认为，虽然 FCN 及其衍生网络都取得了较好的成绩，但本质上都是 encoder-decoder 的结构，所以，该论文作者想要将分割任务构建成一个 sequence-to-sequence 的结构，所以就提出了一个纯 Transformer 的结构（无 CNN 和分辨率降低）。

自从 ViT 证明了 Transformer 在图像分类任务上的的效果后，催生了很多相关的研究。而分割任务可以看做对逐个像素的分类任务，和图像分类有很强的关系，所以 SETR 使用 ViT 作为 backbone，然后使用 CNN 来进行特征图恢复。

框架结构：

• 将图像看做一系列的 image patches
• 然后使用线性映射得到 embedding，并添加 position embedding
• 使用 Transformer 框架进行特征提取
• 使用 conv 进行分辨率恢复

Decoder的作用：生成和原图大小一致的2维分割结果

所以，这里需要把 encoder 的特征 Z 从 $\frac{HW}{256}$ reshape 成 $\frac{H}{16}\times \frac{W}{16}\times C$。

方法一：Naive upsampling (Naive)

① 将transformer得到的特征 $Z^{L_e}$ 映射到分割类别数（如cityscape就是19）

1x1 conv + sync batch norm (with relu) + 1x1 conv

② 使用双线性插值进行上采样，然后计算loss

方法二：Progressive UPsampling （PUP）→ 效果最好

使用渐进上采样，使用卷积核上采样交替变换来实现，为了避免直接上采样多倍带来的误差，这个上采样方法每次只上采样2倍，也就是说如果要把大小为 $\frac{H}{16}\times \frac{W}{16}$ 的 $Z^{L_e}$ 上采样到原图大小，需要进行4次操作。

方法三：Multi-Level feature Aggregation（MLA）

1.7.2 PVT

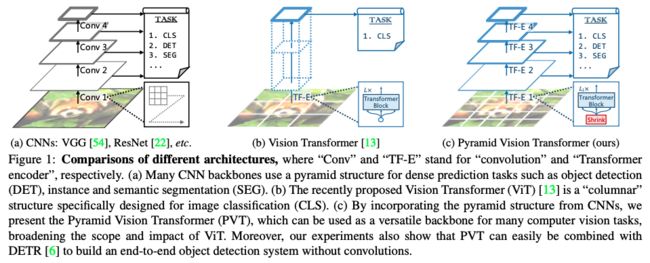
论文： Pyramid vision transformer: A versatile backbone for dense prediction without convolutions

但 ViT 有一些不足：

• ViT 只能输出单一尺度的低分辨率特征
• 在图像上计算量很大

所以 PVT 提出了一种金字塔的 Transformer，能够适用于密集预测。PVT 和 ViT 的主要不同在于：

• ViT 由于高分辨率的计算量和内存问题，只使用了低分辨率特征
• PVT 使用了对密集预测很重要的高分辨率特征，并且使用了 shrinking pyramid 来降低计算量
• PVT 同时有 CNN 和 Transformer 的优势，所以能够用作不同任务的 backbone

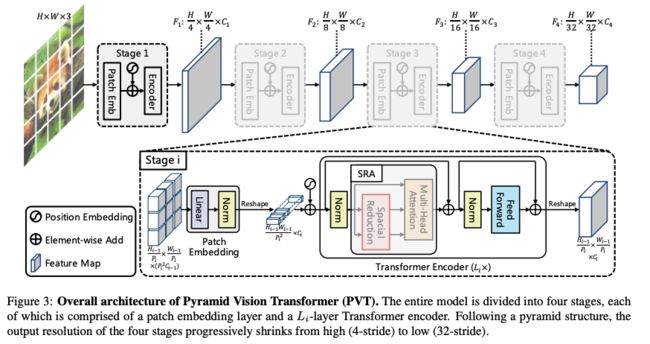
框架结构：

整体框架结构如图 3 所示：

• 有 4 个 stages，分别生成不同尺度的特征图（4x，8x，16x，32x 下采样大小的特征图）
• 所有 stage 的结构都是相同的，包括 1 个 patch embedding 和 $L_i$ 个 Transformer encoder

1.7.3 SegFormer

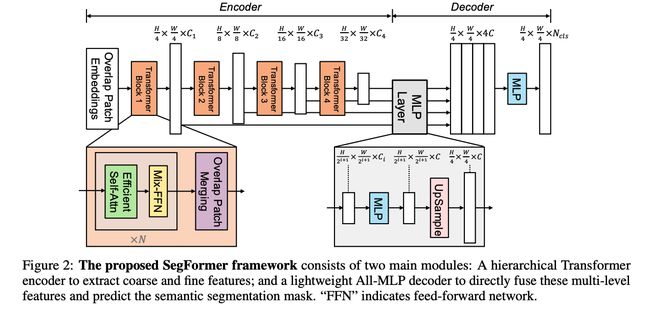
论文：SegFormer：Simple and Efficient Design for Semantic Segmentation with Transformers

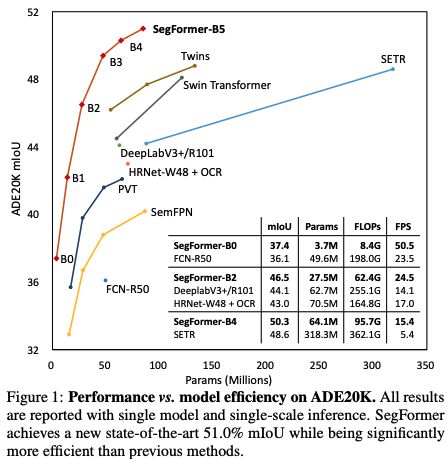
PVT、Swin 和 Twins 等方法，主要考虑设计 encoder，忽略了 decoder 带来的提升，所以作者提出了 SegFormer，同时考虑了效果、效率、鲁棒性，使用了 encoder-decoder 的模式。

框架结构：

• 输入图像大小为 $H\times W\times 3$
• 首先，将图像分为大小为 $4\times 4$ 大小的 patches，patch 越小越有利于密集预测任务
• 接着，将 patches 输入层级 transformer encoder 中，得到多尺度特征，包括原图像大小的 $\{1/4,1/8,1/16,1/32\}$。
• 之后，将这些多尺度特征输入 ALL-MLP decoder 中，预测分割 mask $\frac{H}{4}\times \frac{W}{4}\times N_{cls}$

SegFomer 和 SETR 的区别：

• SegFormer 只使用了 ImageNet-1k 预训练，SETR 中的 ViT 在 ImageNet-22k 上预训练
• SegFormer 的 encoder 是多层级的结构，能够同时捕捉不同分辨率的特征，SETR 的 ViT encoder 只能生成单个分辨率的特征图
• SegFormer 没有使用位置编码，SETR 使用了固定大小的位置编码，会降低准确率
• MLP 的 decoder 比 SETR 的更小更轻量，SETR 需要多个 3x3 的卷积堆叠来实现 decoder。

Hierarchical Transformer Encoder

作者设计了一系列的 Mix Transformer encoders (MiT)，MiT-B0 到 MiT-B5，结构相同，大小不同，MiT-B0 是最轻量级的，可以用来快速推理，MiT-B5 是最重量级的，可以取得最好的效果。

MiT 灵感来源于 ViT，但为适应分割做了一些优化。

① Hierarchical Feature Representation：

给定输入图像 $H\times W\times 3$，作者使用 patch merging 的方法来得到层级特征图 $F_i$，其分辨率为 $\frac{H}{2^{i+1}}\times \frac{W}{2^{i+1}}\times C_i$，其中 $i=\{1,2,3,4\}$，且 $C_{i+1}>C_i$

② Overlapped Patch Merging：

ViT 中，将 $N\times N\times 3$ 的 patch，merge 成了 $1\times 1\times C$ 的特征，所以，作者可以吧特征从 $\frac{H}{4}\times \frac{W}{4}\times C_1$ 变换到 $\frac{H}{8}\times \frac{W}{8}\times C_2$。并且不重叠的 patch 会失去局部连续性，所以作者使用有重叠的 patch merging 方法。

作者的 patch size K=7，相邻 patch 的 stride 为 S=4，padding size P=1，基于此来实现有重叠的 patch merging，得到和无重叠 patch merging 相同大小的结果。

③ Efficient Self-Attention

encoder 中计算量最大的就是 self-attention 层，所以作者使用了文献 [8] 中提出的方法，使用了一个 reduction ratio $R$ 来降低序列的长度：

④ Mix-FFN

ViT 使用 position encoding（PE） 来引入局部位置信息，但是 PE 的分辨率大小是固定的，所以当测试不同于训练图像大小的图像时，需要插值，这样会导致准确率下降。

作者认为 PE 在语义分割中是不需要的，引入了一个 Mix-FFN，考虑了零填充对位置泄露的影响，直接在 FFN 中使用 3x3 的卷积，格式如下：

Mix-FFN 在 FNN 中使用了 3x3 的卷积和 MLP，并且也证明了 3x3 的卷积能够保留位置信息。

Lightweight ALL-MLP Decoder

SegFormer 使用 MLP 构建了一个 Decoder，能够使用 MLP 来实现 decoder 的一个重要原因是，Transformer 有比 CNN 高的感受野。

Decoder 的过程：

• step 1：将多层级特征输入 MLP 层，来规范通道维度
• step 2：将特征图上采样为原图大小的 1/4 大小，concat 起来
• step 3：使用一层 MLP 对特征通道聚合
• step 4：输出预测 segmentation mask $\frac{H}{4}\times \frac{W}{4}\times N_{cls}$

Effective Receptive Field Analysis：

语义分割任务中，保持大的感受野非常重要，所以作者使用 Effective Receptive Field Analysis（ERF）作为工具来可视化并解释为什么 MLP decoder 在 Transformer 上如此有效。

如图 3 所示，作者分别可视化了SegFormer 和 Deeplabv3+ 的 4个 stage 和 decoder head 的 ERF。

• Deeplabv3+ 的 ERF 在每个 stage 都小
• SegFormer 的 encoder 在较低 stage 产生类似于卷积的局部注意，同时也能够在 stage 4 输出非局部的注意，能够有效捕获上下文
• MLP head 的 ERF （蓝框）不同于 stage 4 的红框，蓝框除了 non-local 的attention外，还有更强的局部attention。

所以，MLP 形式的 decoder 能在 Transformer 网络中发挥比 CNN 中更好的作用的原因在于感受野。

这里以训练 cityscapes 为例，来展示其中的要点。

代码运行：

python tools/train.py local_configs/segformer/B1/segformer.b1.1024x1024.city.160k.py

① Encoder 主要过程

• 1、输入 [1,3,1024,1024]，进行 OverlapPatchEmbed，使用核大小为 7，步长为 4 的卷积，生成 [1, 64, 256, 256] 的 patches
• 2、经过 transformer block 1（attention+mlp），特征图大小还是 [1, 64, 256, 256]
• 3、将 block 1 输出的特征图，进行 OverlapPatchEmbed，使用核大小为 3，步长为 2 的卷积，生成 [1, 128, 128, 128] 的 patches
• 4、经过 transformer block 2 （attention+mlp），特征图大小还是 [1, 128, 128, 128]
• 5、将 block 2 输出的特征图，进行 OverlapPatchEmbed，使用核大小为 3，步长为 2 的卷积，生成 [1, 320, 64, 64] 的 patches
• 6、经过 transformer block 3 （attention+mlp），特征图大小还是 [1, 320, 64, 64]
• 7、将 block 3 输出的特征图，进行 OverlapPatchEmbed，使用核大小为 3，步长为 2 的卷积，生成 [1, 512, 32, 32] 的 patches
• 8、经过 transformer block 4 （attention+mlp），特征图大小还是 [1, 512, 32, 32]

四个 stage 的输出被 concat 成为一个 list，也就是四种不同分辨率大小的多层级特征图。

transformer block 1 如下：

ModuleList(
  (0): Block(
    (norm1): LayerNorm((64,), eps=1e-06, elementwise_affine=True)
    (attn): Attention(
      (q): Linear(in_features=64, out_features=64, bias=True)
      (kv): Linear(in_features=64, out_features=128, bias=True)
      (attn_drop): Dropout(p=0.0, inplace=False)
      (proj): Linear(in_features=64, out_features=64, bias=True)
      (proj_drop): Dropout(p=0.0, inplace=False)
      (sr): Conv2d(64, 64, kernel_size=(8, 8), stride=(8, 8))
      (norm): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
    )
    (drop_path): Identity()
    (norm2): LayerNorm((64,), eps=1e-06, elementwise_affine=True)
    (mlp): Mlp(
      (fc1): Linear(in_features=64, out_features=256, bias=True)
      (dwconv): DWConv(
        (dwconv): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), groups=256)
      )
      (act): GELU()
      (fc2): Linear(in_features=256, out_features=64, bias=True)
      (drop): Dropout(p=0.0, inplace=False)
    )
  )
  (1): Block(
    (norm1): LayerNorm((64,), eps=1e-06, elementwise_affine=True)
    (attn): Attention(
      (q): Linear(in_features=64, out_features=64, bias=True)
      (kv): Linear(in_features=64, out_features=128, bias=True)
      (attn_drop): Dropout(p=0.0, inplace=False)
      (proj): Linear(in_features=64, out_features=64, bias=True)
      (proj_drop): Dropout(p=0.0, inplace=False)
      (sr): Conv2d(64, 64, kernel_size=(8, 8), stride=(8, 8))
      (norm): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
    )
    (drop_path): DropPath()
    (norm2): LayerNorm((64,), eps=1e-06, elementwise_affine=True)
    (mlp): Mlp(
      (fc1): Linear(in_features=64, out_features=256, bias=True)
      (dwconv): DWConv(
        (dwconv): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), groups=256)
      )
      (act): GELU()
      (fc2): Linear(in_features=256, out_features=64, bias=True)
      (drop): Dropout(p=0.0, inplace=False)
    )
  )
)

② SegFormer Head

• 1、输入为上面的 4 种不同分辨率的输出
• 2、经过4层 MLP 和 上采样（每个 stage 的特征分别经过一个 MLP，参数不共享，上采样到最大特征图的大小）
• 3、4 层特征concat，得到 [1, 1024, 256, 256] 维特征，然后经过 Conv+BN+ReLU，得到 [1, 256, 256, 256]
• 4、线性映射为 [1, 19, 256, 256]，作为预测 segmentation mask

# MLP 1 (for the feature from stage 4)
MLP(
  (proj): Linear(in_features=512, out_features=256, bias=True)
)
resize

# MLP 2
MLP(
  (proj): Linear(in_features=320, out_features=256, bias=True)
)
resize

# MLP 3
MLP(
  (proj): Linear(in_features=128, out_features=256, bias=True)
)
resize

# MLP 4
MLP(
  (proj): Linear(in_features=64, out_features=256, bias=True)
)
resize

# 特征融合
ConvModule(
  (conv): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
  (bn): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (activate): ReLU(inplace=True)
)

1.7.4 HRFormer

NeurIPS 2021

论文：HRFormer：High-Resolution Transformer for Dense Prediction

HRFormer 是一个针对密集预测任务提出的方法，不同于 ViT 系列只使用低分辨率特征的方法。

ViT 系列的方法在分类任务上的优势有目共睹，其将图像切分为小块，分别提取小块中的特征，网络输出是单个分辨率的，缺失了处理多尺度目标的能力。

HRFormer 能够提取多尺度空间信息，为密集预测提供多分辨率特征表达。

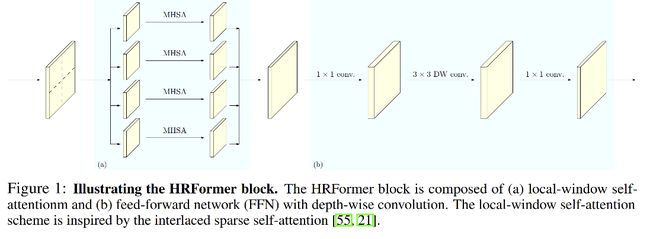
HRFormer block：

如何减少计算量：

• 在每个分辨率特征图内部，作者都使用了 local-window self-attention 来减少计算量，作者将特征图无重叠的划分为小的 windows，然后在每个 window 内部分别使用 self-attention
• 并且，为了进行不同 window 间的信息交互，作者在 local-window self-attention 后面的前传网络 FFN 中引入了 3x3 的可分离卷积，有助于提高感受野

HRFormer 框架结构：

• Local-window self-attention：将特征图切成不重叠的块，在每个块（window）内进行多头自注意力计算（MHSA）
• 在 FFN 中的 MLP 之间添加 3x3 的可分离卷积，进行 windows 之间的信息交换

HRFormer 的输出包含了 4 种不同分辨率的特征图，对于不同的任务，作者罗列了不同的 head 设计方法：

• 分类任务：把 4 个特征图送入 bottleneck，输出通道变化为 128、256、512、1024，然后使用卷积将它们聚合起来，输出一个最低维的特征图，最后使用avgpooling。
• 姿态估计任务：仅仅使用最高维度的特征图
• 语义分割任务：将所有的特征图上采样到相同的大小，然后concat起来

1.7.5 PoolFormer

论文：PoolFormer: MetaFormer is Actually What You Need for Vision

Transformer 最近在计算机视觉任务上展示了很好的效果，大家基本上都认为这种成功来源于基于 self-attention 的结构。但又有文章证明，只使用 MLP 也能达到很好的效果，所以作者假设 Transformer 的效果来源于 transformer 的结构，而非将 token 进行融合交互的模块。

所以，作者使用简单的 spatial pooling 模块替换了 attention 模块，来实现 token 之间的信息交互，称为 PoolFormer，也能达到很好的效果。

在 ImageNet-1K 上达到了 82.1% 的 top-1 acc。

作者使用 PoolFormer 证明了他们的猜想，并且提出了 “MetaFormer” 的概念，也就是一种从 Transformer 中抽象出来的结构，没有特殊的 token mixer 方式。

框架结构：

1、MetaFormer

MetaFormer 其实是 Transformer 的一个抽象，其他部分和 Transformer 保持一致，token mixer 方式是不特殊指定的。

① 首先，输入 $I$ 经过 embedding：
$$X=Input\_Emd(I)$$

② 然后，将 embedding token 输入 MetaFormer blocks，该 block 包含两个残差 sub-blocks

• 第一个 sub-block：token mixer，即在 tokens 之间进行信息传递

$$Y=Token\_Mixer(Norm(X))+X$$

• 第二个 sub-block：两个 MLP & 激活层
  $$Z=\sigma (Norm(Y)W_1)W_2+Y$$

2、PoolFormer

作者为了证明猜想，使用了非常简单的 pooling 算子来实现 token mixer，没有任何可学习参数。

假设输入形式为 $T\in R^{C\times H\times W}$，channel 维度在前，则 pooling 操作如下，$k$ 为 pooling 大小：

作者使用 PoolFormer 作为 Semantic FPN 的主干网络，使用 mmsegmentation 训练的结果如下。超越了基于 CNN 的网络。

二、2D 数据集介绍

2.1 PASCAL Visual Object Classes (VOC)

可以支持 5 类任务：分类、分割、检测、姿势识别、人体。

对于分割任务，共支持 21 个类别，训练和验证各 1464 和 1449 张图：

vehicles, household, animals, aeroplane, bicycle, boat, bus, car, motorbike, train, bottle, chair, dining table, potted plant, sofa, TV/monitor, bird, cat, cow, dog, horse, sheep, and person

2.2 PASCAL Context

是 VOC 2010 检测比赛的扩充集，包含 400 个类别，三个大类（objects、stuff、hybrids），经常只使用 59 个常见类别。

2.3 Microsoft Common Objects in Context (MS COCO)

共包括 91 个类别，328k 图像，2.5 million 带 label 的实例。

检测任务共包含 80 个类别，82k 训练，40.5 验证。

2.4 Cityscapes

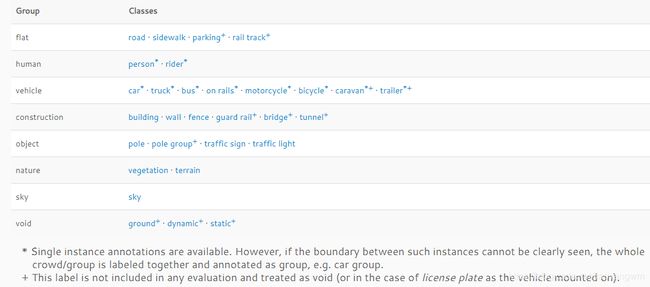
街景数据集，包含 5k 精细标注数据，20k 粗糙标注数据。标注了 30 个类别。

• 5000张精细标注：2975张训练图，500张训练图，1525张测试图
• 20000张粗糙标注(使用多边形覆盖单个对象)
• 图像大小：1024x2048
• 50个不同城市的街景，train/val/test的城市都不同

类别定义：

• *：是针对单个实例进行标注的，如果同一类别的多个物体交叉分布，也即实例边界不明显，这些物体组成一个单一实例的group，如 car/bicycle group.
• +: 表示的label目前还没有包含在任何的评估项中，treated as void；所以去掉这些label，一般我们说CityScapes包含19类。

2.5 ADE20K/MIT Scene Parsing

包含 20k 训练，2k 验证数据，共 150 个类别。

2.6 Mapillary

Mapillary Vistas 数据集包含 66 类共 25,000 张高分辨率街景场景的数据，其中有 37 个类是以实例区分的标签。数据总量是 cityscapes 的5倍之多，包括不同天气、季节、时间。采集方式包括手机、摄像机、电脑、运动相机等。

• 数据总量：25k
• 训练总量：18k
• 验证总量：2k
• 测试总量：5k

官网：https://www.mapillary.com/

三、评价指标

3.1 Pixel accuracy

对于 K+1 个类别（K 类目标，1 类背景），PA 计算如下：

其中，$p_{ij}$ 是第 i 个类别预测为第 j 个类别的总量

3.2 Mean Pixel Accuracy（MPA）

是 PA 的扩展，对每个类别分别计算，然后求平均

3.3 IoU

是语义分割中的一个很重要的衡量指标，表示的是预测的 map 和 gt map 之间的交并比：

$$IoU=\frac{TP}{TP+FP+FN}$$

语义分割中，IoU是用mask来评价的：

GT：

Prediction：

Intersection：

Union：

mIoU：各个类别的IoU的均值

mIoU 的计算：

• 步骤一：先求混淆矩阵
• 步骤二：再求mIoU

混淆矩阵：

真实情况	预测结果	预测结果
真实情况	正例	反例
正例	TP	FN
反例	FP	TN

混淆矩阵的对角线上的值表示预测正确的值，IoU是只求正例的IoU，如何找出和正例有关的混淆矩阵元素呢，可以通过划线法来得到，

假设有N个类别，则混淆矩阵就是一个NxN的矩阵，对角表示TP，横看真实，竖看预测。

假设一个3类的预测输出的混淆矩阵如下所示：

真实	预测	预测	预测
真实	0	1	2
0	3	0	0
1	0	2	1
2	0	1	2

• 对角线上的元素表示预测类别正确的像素数目
• 每一行表示该类别真实的像素个数
• 每一列表示预测为该类别的像素个数

真实	预测	预测	预测
真实	0	1	2
0	a	b	c
1	d	e	f
2	g	h	i

精确率：

$precisio{n}_0=a/(a+d+g)$
$precisio{n}_1=e/(b+e+h)$
$precisio{n}_2=i/(c+f+i)$

$precisio{n}_0=3/(3+0+0)=1$
$precisio{n}_1=2/(2+1+0)=2/3$
$precisio{n}_2=2/(2+1+0)=2/3$

召回率：

$recal{l}_0=a/(a+b+c)$
$recal{l}_1=e/(d+e+f)$
$recal{l}_2=i/(g+h+i)$

$recal{l}_0=3/(3+0+0)$
$recal{l}_1=2/(2+1+0)=2/3$
$recal{l}_2=2/(2+1+0)=2/3$

CPA：Class Pixel Accuracy(每类的像素精度)→按类别计算正确的像素占总像素的比例

$$P_i=对角线值/对应列的像素总数$$
$$p_0=3/(3+0+0)=1$$
$$p_1=2/(0+2+1)=0.67$$
$$p_2=2/(0+1+2)=0.67$$

MPA：Mean Pixel Accuracy→每类正确分类像素比例的平均
$$MPA=sum(p_i)/类别数=(1+0.67+0.67)/3=0.78$$

IoU：

• 划线法：
  $$Io{U}_0=3/(3+0+0+0+0)=1$$
  $$Io{U}_1=2/(0+2+1+1+1)=0.5$$
  $$Io{U}_2=2/(0+1+2+2+1)=0.5$$

• 代码方法：$S_{A\cup B}=S_A+S_B-S_{A\cap B}$
  $$Io{U}_0=3/[(3+0+0)+(3+0+0)-3]=1$$
  $$Io{U}_1=2/[(0+2+1)+(1+2+1)-2]=0.5$$
  $$Io{U}_2=2/[(0+1+2)+(0+2+1)-2]=0.5$$

mIoU：

$$mIoU=sum(Io{U}_i)/class$$

import numpy as np

class IOUMetric:
    """
    Class to calculate mean-iou using fast_hist method
    """

    def __init__(self, num_classes):
        self.num_classes = num_classes
        self.hist = np.zeros((num_classes, num_classes))

    def _fast_hist(self, label_pred, label_true):
    	# 找出标签中需要计算的类别,去掉了背景
        mask = (label_true >= 0) & (label_true < self.num_classes)
        # np.bincount计算了从0到n**2-1这n**2个数中每个数出现的次数，返回值形状(n, n)
        hist = np.bincount(
            self.num_classes * label_true[mask].astype(int) +
            label_pred[mask], minlength=self.num_classes ** 2).reshape(self.num_classes, self.num_classes)
        return hist

   # 输入：预测值和真实值
    # 语义分割的任务是为每个像素点分配一个label
    def evaluate(self, predictions, gts):
    	 for lp, lt in zip(predictions, gts):
            self.hist += self._fast_hist(lp.flatten(), lt.flatten())
        #miou
        iou = np.diag(self.hist) / (self.hist.sum(axis=1) + self.hist.sum(axis=0) - np.diag(self.hist))
        miou = np.nanmean(iu)
        #其他性能指标
        acc = np.diag(self.hist).sum() / self.hist.sum()
        acc_cls = np.nanmean(np.diag(self.hist) / self.hist.sum(axis=1))
        freq = self.hist.sum(axis=1) / self.hist.sum()
        fwavacc = (freq[freq > 0] * iu[freq > 0]).sum()
        return acc, acc_cls, iou, miou, fwavacc

3.4 Mean-IoU

是所有类别 IoU 求平均

3.5 Precision/Recall/F1 score

3.6 Dice coefficient

类似于 IoU：

当为二值 map 时，等于 F1 score

四、Loss 函数

代码链接：https://github.com/shruti-jadon/Semantic-Segmentation-Loss-Functions

分割的 loss 函数可以被大体分为 4 个大类：

• Distribution-based
• Region-based
• Boundary-based
• Compounded

4.1 Cross-Entropy loss

Cross-entropy 是衡量两个概率分布的距离的量，一般被用作分类的目标函数，分割作为一个像素级别分类的任务，也同样可以使用该函数作为目标函数。

1、Binary Cross-entropy

信息量：用来衡量一个事件所包含的信息大小，一个事件发生的概率越大，则不确定性越小，信息量越小。公式如下，从公式中可以看出，信息量是概率的负对数：
$$h(x)=-lo{g}_{2}p(x)$$

熵：用来衡量一个系统的混乱程度，代表系统中信息量的总和，是信息量的期望，信息量总和越大，表明系统不确定性就越大。

$$Entropy=-\sum plog(p)$$

交叉熵：用来衡量实际输出和期望输出的接近程度的量，交叉熵越小，两个概率分布就越接近。
$$L=\sum _{c=1}^M{y}_{c}log(p_c)$$
其中，M表示类别数，$y_c$是label，即one-hot向量，$p_c$是预测概率，当M=2时，就是二元交叉熵损失

pytorch中的交叉熵：

Pytorch中CrossEntropyLoss()函数的主要是将softmax-log-NLLLoss合并到一块得到的结果。

• Softmax后的数值都在0~1之间，所以ln之后值域是负无穷到0。
• 然后将Softmax之后的结果取log，将乘法改成加法减少计算量，同时保障函数的单调性 。
• NLLLoss的结果就是把上面的输出与Label对应的那个值拿出来，去掉负号，再求均值。

交叉熵loss可以用到大多数语义分割场景中，但他有一个明显的缺点，对于只用分割前景和背景时，前景数量远远小于背景像素的数量，损失函数中y=0的成分就会占据主导，使得模型严重偏向背景，导致效果不好。

语义分割 cross entropy loss计算方式：

输入 model_output=[2, 19, 128, 256] # 19 代表输出类别
标签 target=[2, 512,1024]

1、将model_output的维度上采样到 [512, 1024]

2、softmax处理：这个函数的输入是网络的输出预测图像，输出是在dim=1（19）上计算概率。输出维度不变，dim=1维度上的值变成了属于每个类别的概率值。

x_softmax = F.softmax(x,dim=1)

3、log处理：

log_softmax_output = torch.log(x_softmax)

4、nll_loss 函数（negative log likelihood loss）：这个函数目的就是把标签图像的元素值，作为索引值，在temp3中选择相应的值，并求平均。

output = nn.NLLLoss(log_softmax_output, target)

如果第一个点真值对应的3，则在预测结果中第3个通道去找该点的预测值，假设该点预测结果为-0.62，因为是loss前右负号，则最终结果变为0.62。其余结果依次类推，最后求均值即时最终损失结果。

• 当一个点真实类别=3时，假设其对应第三个类别的特征图上的点为0.9，则其-log的结果非常接近0，此时loss会非常小
• 当一个点真实类别=3时，假设其对应第三个类别的特征图上的点为0.2，则其-log的结果会比较大，此时loss会非常大

二值 Cross-entropy 公式如下：

其中，$\hat{y}$ 是预测的结果，$y$ 是真实结果

2、Weighted Binary Cross-entropy

Weighted Binary Cross-entropy（WCE） 是二值 cross-entropy 函数的变体，正样本会通过加权系数来得到权重的加强。适用于分布较倾斜的数据，如下图所示。

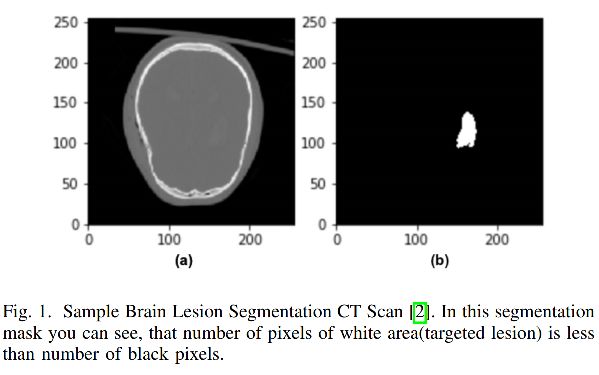
Weighted Binary Cross-entropy 公式如下：

其中：

• $\beta$ 可以被用来调整假负和假正样本
• 如果需要降低假负样本的数量，可以设置 $\beta >1$
• 如果需要降低假正样本的数量，可以设置 $\beta <1$

2、Balanced Cross-entropy

Balanced cross entropy (BCE) 类似于 WCE，唯一的不同在于正样本，

BCE 的公式如下：

其中：$\beta =1-\frac{y}{H\ast W}$，相比原来的loss，在样本数量不均衡的情况下可以获得更好的效果。

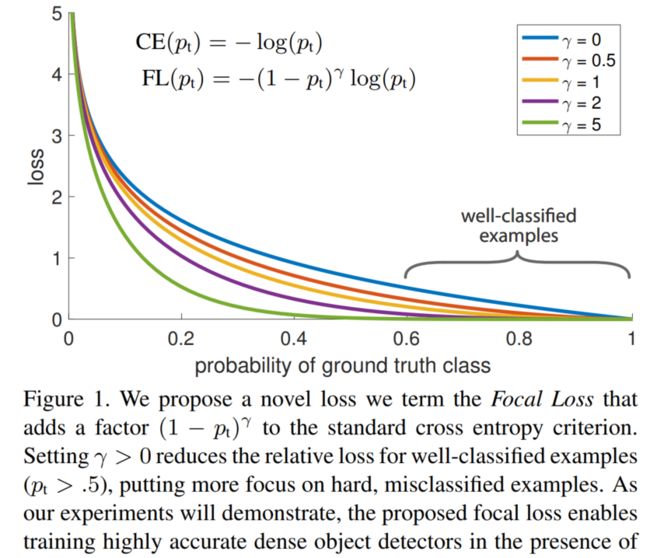
4.2 Focal loss

Focal loss 可以被看做 Binary Cross-entropy loss 的变体，特点如下：

• FL 将简单样本的权重变小，让模型更关注难样本
• 对类别极度不平衡的场景表现好。

Focal loss 其实是源于 Cross-entropy loss 的，目的是解决样本数量不平衡的情况:

• 正样本loss增加，负样本loss减小
• 难样本loss增加，简单样本loss减小

一般分类时候通常使用交叉熵损失：

$$CrossEntropy(p,y)=\{\begin{array}{ll}-log(p),& y=1\\ -log(1-p),& y=0\end{array}$$

为了解决正负样本数量不平衡的问题，我们经常在二元交叉熵损失前面加一个参数 $\alpha$。负样本出现的频次多，那么就降低负样本的权重，正样本数量少，就相对提高正样本的权重。因此可以通过设定$\alpha$的值来控制正负样本对总的loss的共享权重。$\alpha$取比较小的值来降低负样本（多的那类样本）的权重。即：

$$CrossEntropy(p,y)=\{\begin{array}{ll}-\alpha log(p),& y=1\\ -(1-\alpha )log(1-p),& y=0\end{array}$$

虽然平衡了正负样本的数量，但实际上，目标检测中大量的候选目标都是易分样本。这些样本的损失很低，但是由于数量极不平衡，易分样本的数量相对来讲太多，最终主导了总的损失。

因此，这篇论文认为易分样本（即，置信度高的样本）对模型的提升效果非常小，模型应该主要关注与那些难分样本 。一个简单的想法就是只要我们将高置信度样本的损失降低一些, 也即是下面的公式：
$$Focal\_Loss=\{\begin{array}{ll}-(1-p{)}^{\gamma }log(p),& y=1\\ -p^{\gamma }log(1-p),& y=0\end{array}$$

当$\gamma =0$ 时，即为交叉熵损失函数，当其增加时，调整因子的影响也在增加，实验发现为2时效果最优。

假设取$\gamma =2$，如果某个目标置信得分p=0.9，即该样本学的非常好，那么这个样本的权重为 $(1-0.9{)}^2=0.001$，损失贡献降低了1000倍。

为了同时平衡正负样本问题，Focal loss还结合了加权的交叉熵loss，所以两者结合后得到了最终的Focal loss：

$$Focalloss=\{\begin{array}{ll}-\alpha (1-p{)}^{\gamma }log(p),& y=1\\ -(1-\alpha )p^{\gamma }log(1-p),& y=0\end{array}$$

取 $\alpha =0.25$ 在文中，即正样本要比负样本占比小，这是因为负样本易分。

单单考虑alpha的话，alpha=0.75时是最优的。但是将gamma考虑进来后，因为已经降低了简单负样本的权重，gamma越大，越小的alpha结果越好。最后取的是alpha=0.25，gamma=2.0

https://zhuanlan.zhihu.com/p/49981234

class FocalLoss(nn.Module):
    def __init__(self, gamma=0, alpha=None, size_average=True):
        super(FocalLoss, self).__init__()
        self.gamma = gamma
        self.alpha = alpha
        if isinstance(alpha,(float,int,long)): self.alpha = torch.Tensor([alpha,1-alpha])
        if isinstance(alpha,list): self.alpha = torch.Tensor(alpha)
        self.size_average = size_average

    def forward(self, input, target):
        if input.dim()>2:
            input = input.view(input.size(0),input.size(1),-1)  # N,C,H,W => N,C,H*W
            input = input.transpose(1,2)    # N,C,H*W => N,H*W,C
            input = input.contiguous().view(-1,input.size(2))   # N,H*W,C => N*H*W,C
        target = target.view(-1,1)

        logpt = F.log_softmax(input)
        logpt = logpt.gather(1,target)
        logpt = logpt.view(-1)
        pt = Variable(logpt.data.exp())

        if self.alpha is not None:
            if self.alpha.type()!=input.data.type():
                self.alpha = self.alpha.type_as(input.data)
            at = self.alpha.gather(0,target.data.view(-1))
            logpt = logpt * Variable(at)

        loss = -1 * (1-pt)**self.gamma * logpt
        if self.size_average: return loss.mean()
        else: return loss.sum()

4.3 Dice Loss

Dice Loss：
$$Dice\_Loss=1-Dice\_Coefficient$$

Dice 系数：

根据 Lee Raymond Dice命名，是一种集合相似度度量函数，通常用于计算两个样本的相似度(值范围为 [0, 1])，公式如下，分子有2是因为分母加了两次TP：

$$DiceCoefficient=\frac{2|X\cap Y|}{|X|+|Y|}$$

其中，$|X|$和$|Y|$分别表示集合的元素个数，分割任务中，两者分别表示GT和预测。

所以 Dice Loss 公式如下：

$$DiceLoss=1-\frac{2|X\cap Y|}{|X|+|Y|}$$

从IoU过度到Dice：

• 黄色区域：预测为negative，但是GT中是positive的False Negative区域；
• 红色区域：预测为positive，但是GT中是Negative的False positive区域；

IoU的算式：

$$IoU=\frac{TP}{TP+FP+FN}$$

简单的说就是，重叠的越多，IoU越接近1，预测效果越好。

Dice 系数：

$$Dice\_Coefficient=\frac{2|X\cap Y|}{|X|+|Y|}$$

• $|X\cap Y|$ → $TP$
• $X$ 是 $GT$ → $TP+FN$
• $Y$ 是 $Pred$→$TP+FP$

所以：
$$Dice\_Coefficient=\frac{2\times TP}{TP+FN+TP+FP}$$

所以我们可以得到Dice和IoU之间的关系了，这里的之后的Dice默认表示Dice Coefficient：

$$IoU=\frac{Dice}{2-Dice}$$

这个函数图像如下图，我们只关注0～1这个区间就好了，可以发现：

• IoU和Dice同时为0，同时为1；这很好理解，就是全预测正确和全部预测错误
• 假设在相同的预测情况下，可以发现Dice给出的评价会比IoU高一些，哈哈哈。所以Dice的数据会更加好看一些。

需要注意的是Dice Loss存在两个问题：

• 训练误差曲线非常混乱，很难看出关于收敛的信息。尽管可以检查在验证集上的误差来避开此问题。

• Dice Loss比较适用于样本极度不均的情况，一般的情况下，使用 Dice Loss 会对反向传播造成不利的影响，容易使训练变得不稳定。

所以在一般情况下，还是使用交叉熵损失函数。

Dice coefficient 通常被用来度量两幅图像的相似度，Dice loss 公式如下：

其中，分母分子分别加 1，是为了保证边缘情况的可用性，如当 $y=\hat{p}=0$ 时。

4.4 Tversky Loss

Tversky index(TI) 也可以被看成 Dice coefficient 的一种扩展：

当 $\beta =1/2$ 时，就是 Dice coefficient。

Tversky loss 公式如下：