吴恩达机器学习ex5-matlab版学习总结笔记-正则化线性回归和偏差方差
作业任务项一:正则化线性回归
代码如下:
load('E:\研究生\机器学习\吴恩达机器学习python作业代码\code\ex5-bias vs variance\ex5data1.mat')
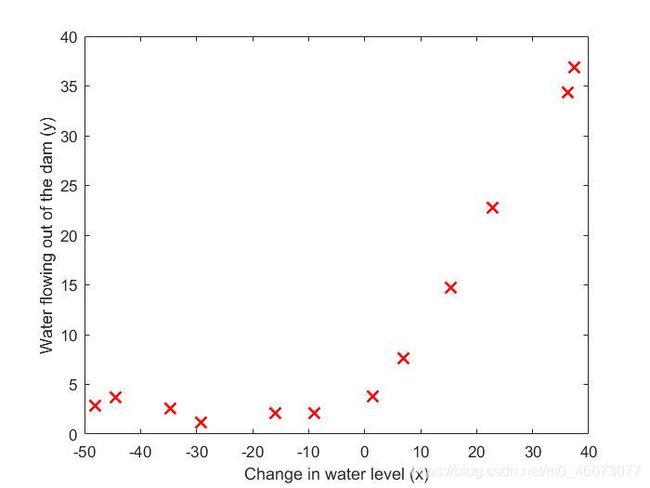
plot(X,y,'rx','markersize',10,'linewidth',1.5);
xlabel('Change in water level (x)');
ylabel('Water flowing out of the dam (y)');
| 图1 原始数据图像 |
|---|
初始化及验证部分如下:
% 初始化
theta=[1;1];
lambda=1;
X1=[ones(size(X,1),1),X];
%验证部分
[J,grad]=linearRegCostFunction(X1,y,theta,lambda);
fprintf('\nCost:%f\n',J);
fprintf('Expected cost:303.993\n');
fprintf('Gradients:\n');
fprintf('%f \n',grad);
fprintf('Expected gradients:\n');
fprintf('-15.30\n 598.250\n');
其中linearRegCostFunction.m如下:
function [J,grad]=linearRegCostFunction(x,y,theta,lambda)
if ~exist('lambda','var')||isempty(lambda)
lambda=0;
end
m=length(y);
J=0;
grad=zeros(size(theta));
theta_1=[0;theta(2:end)];
J=1/2/m*(x*theta-y)'*(x*theta-y)+lambda/2/m*theta_1'*theta_1;
grad=1/m*sum((x*theta-y) .* x)+lambda/m*theta_1';
grad=grad(:);
end
训练部分和绘图部分如下:
theta=trainLinearReg(X1,y,lambda);
y1=X1*theta;
hold on
plot(X,y1,'--','linewidth',2);
[error_train,error_val]=learningCurve(X,y,...
Xval,yval,lambda);
figure
plot(1:numel(error_train),error_train,'b',1:numel(error_val),error_val,'g');
xlabel('Number of training examples');
ylabel('Error');
legend('Train','Cross Validation');
其中trainLinearReg.m如下:
fmincg.m在网上找就可以了,是一个高级优化算法。
function theta=trainLinearReg(x,y,lambda)
initial_theta = zeros(size(x, 2), 1);
options=optimset('Gradobj','on','MaxIter',200);
[theta]=fmincg(@(t)linearRegCostFunction(x,y,t,lambda),initial_theta,options);
通过优化函数找到theta,并求出假设直线y1,得到图2正则化线性回归如下:
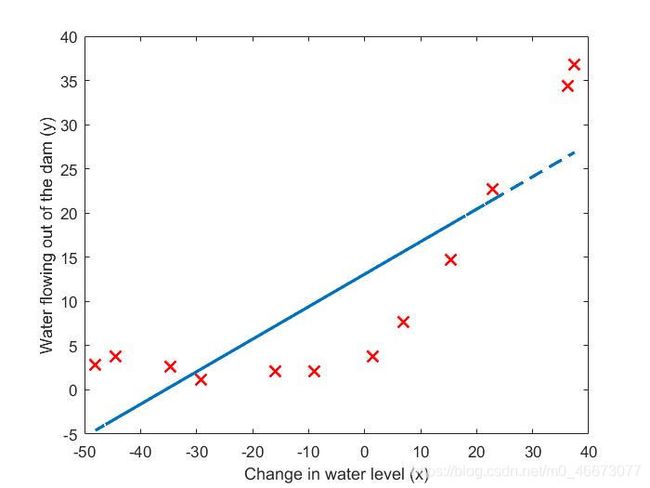
| 图2 正则化线性回归 |
|---|
其中learningCurve.m如下:
通过逐次输入数据(第一次一个实例,第二次两个实例,…,最后一次用所有实例)训练得到theta,再用每次得到的theta交给训练集和交叉验证集得到每次的error,也就是代价函数,其中训练集需要逐次计算代价函数,而交叉验证集直接使用所有实例进行theta的验证。
function [error_train,error_val]=learningCurve(x,y,Xval,yval,lambda)
m=size(x,1);
error_train=zeros(m,1);
error_val=zeros(m,1);
for i=1:m
theta=trainLinearReg(x(1:i,:),y(1:i),lambda);
[error_train(i),~]=linearRegCostFunction(x(1:i,:),y(1:i),theta,0);
[error_val(i),~]=linearRegCostFunction(Xval,yval,theta,0);
end
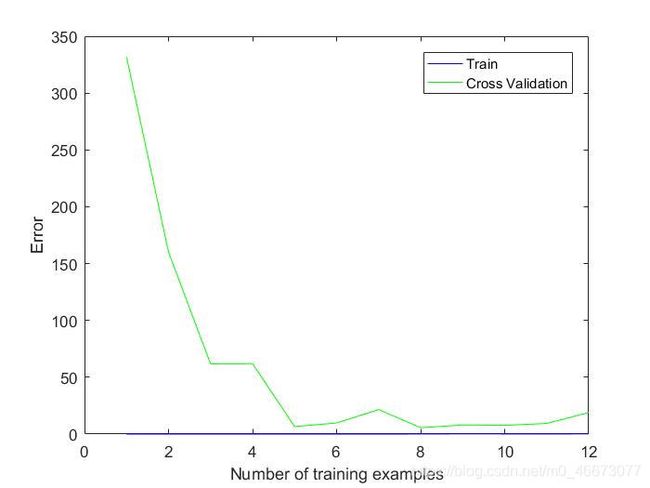
最后得到结果图3所示,可以看出,当训练集误差和交叉验证误差近似时属于高偏差/欠拟合。
| 图3 学习曲线 |
|---|
作业任务项二:正则化多项式回归
假设函数公式为:
h θ ( x ) = θ 0 + θ 1 ∗ ( w a t e r L e v e l ) + θ 2 ∗ ( w a t e r L e v e l ) 2 + ⋅ ⋅ ⋅ + θ p ∗ ( w a t e r L e v e l ) p = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ p x p . h_θ(x) = θ_0+ θ_1∗ (waterLevel) + θ_2∗ (waterLevel)^2+ · · · + θ_p∗ (waterLevel)^p= θ_0+ θ_1x^1+ θ_2x^2+ ... + θ_px^p. hθ(x)=θ0+θ1∗(waterLevel)+θ2∗(waterLevel)2+⋅⋅⋅+θp∗(waterLevel)p=θ0+θ1x1+θ2x2+...+θpxp.
代码如下:
load('E:\研究生\机器学习\吴恩达机器学习python作业代码\code\ex5-bias vs variance\ex5data1.mat')
p=8;
m=size(X,1);
%polynomial and normalize
X_poly=polyFeatures(X,p);
[X_norm,mu,sigma]=featureNormalize(X_poly);
X_norm = [ones(m, 1), X_norm];
X_poly_test = polyFeatures(Xtest, p);
X_poly_test = bsxfun(@minus, X_poly_test, mu);
X_poly_test = bsxfun(@rdivide, X_poly_test, sigma);
X_poly_test = [ones(size(X_poly_test, 1), 1), X_poly_test];
X_poly_val = polyFeatures(Xval, p);
X_poly_val = bsxfun(@minus, X_poly_val, mu);
X_poly_val = bsxfun(@rdivide, X_poly_val, sigma);
X_poly_val = [ones(size(X_poly_val, 1), 1), X_poly_val];
lambda=0;
theta=trainLinearReg(X_norm,y,lambda);
plot(X,y,'rx','markersize',10,'linewidth',1.5);
xlabel('Change in water level (x)');
ylabel('Water flowing out of the dam (y)');
title (sprintf('Polynomial Regression Fit (lambda = %f)', lambda));
%plot
hold on
xx=(min(X)-15:0.05:max(X)+15)';
xx_poly=polyFeatures(xx,p);
xx_poly = bsxfun(@minus, xx_poly, mu);
xx_poly = bsxfun(@rdivide, xx_poly, sigma);
xx_poly = [ones(size(xx, 1), 1) ,xx_poly];
plot(xx, xx_poly * theta, '--', 'LineWidth', 2);
hold off
[error_train,error_val]=learningCurve(X_norm,y,...
X_poly_val,yval,lambda);
figure
plot(1:numel(error_train),error_train,'b',1:numel(error_val),error_val,'g');
xlabel('Number of training examples');
ylabel('Error');
legend('Train','Cross Validation');
p为自定的多项式阶数,之后进行多项式的变换以及特征缩放。
其中polyFeatures.m如下:
这个函数目的是将一次方的x转化为多次方的x,第一列为一次方,…,第p列为p次方。
function X_poly=polyFeatures(x,p)
X_poly=zeros(size(x,1),p);
for i=1:p
X_poly(:,i)=x.^(i);
end
其中featureNormalize.m如下:
这是一个ex1中出现过的特征缩放函数。
function [X_norm mu sigma]=featureNormalize(X)
X_norm=X;
mu=zeros(1,size(X,2));
sigma=zeros(1,size(X,2));
for i=1:size(X,2)
mu(i)=mean(X_norm(:,i));
sigma(i)=std(X_norm(:,i));
end
X_norm=(X_norm-ones(size(X,1),1)*mu)./(ones(size(X,1),1)*sigma);
end
训练集数据多项化和特征缩放之后,得到的平均值和均方差要供交叉验证集和测试集特征缩放使用。因此交叉验证集和测试集多项化以后要用bsxfun函数进行处理,完成特征缩放。
绘图部分中,xx是绘图时x轴方向上的分段,同样通过多项化和特征缩放以后可以theta相乘得到预测值,再把xx上的预测值画出来。
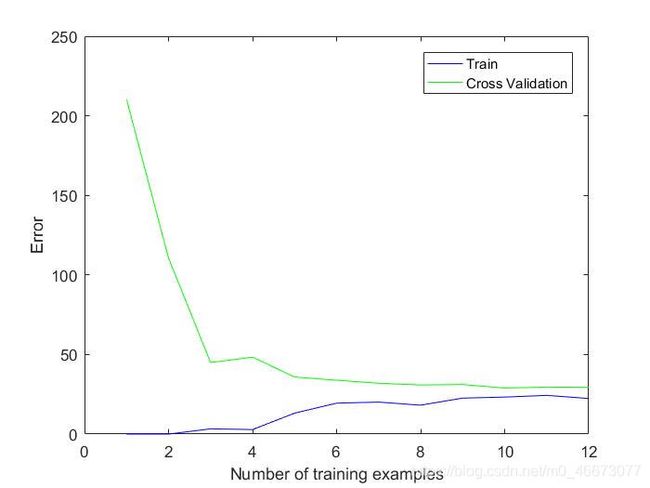
最后用相同的方法计算学习曲线,得到图像如图4和图5所示:
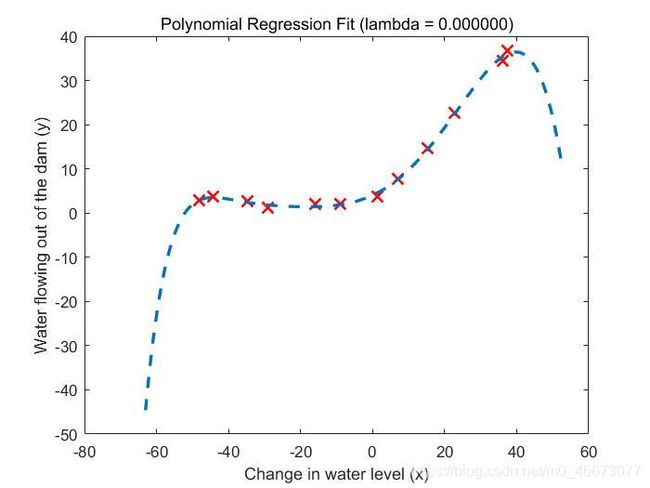
| 图4 λ = 0 \lambda=0 λ=0多项式回归结果 |
|---|
| 图5 多项式回归学习曲线 |
|---|
作业任务项三(选做): λ \lambda λ的选择
代码如下:
[lambda_vec,error_train,error_val,error_test]=validationCurve(X_norm,y,X_poly_val,yval,X_poly_test,ytest);
plot(lambda_vec,error_train,lambda_vec,error_val);
legend('Train', 'Cross Validation');
xlabel('lambda');
ylabel('Error');
其中validationCurve.m如下:
function [lambda_vec,error_train,error_val,error_test]=validationCurve(x,y,xval,yval,xtest,ytest)
lambda_vec=[0 0.001 0.003 0.01 0.03 0.1 0.3 1 3 10]';
error_train=zeros(length(lambda_vec),1);
error_val=zeros(length(lambda_vec),1);
error_test=zeros(length(lambda_vec),1);
for i=1:length(lambda_vec)
theta=trainLinearReg(x,y,lambda_vec(i));
error_train(i)=linearRegCostFunction(x,y,theta,lambda_vec(i));
error_val(i)=linearRegCostFunction(xval,yval,theta,lambda_vec(i));
error_test(i)=linearRegCostFunction(xtest,ytest,theta,lambda_vec(i));
end
将各个lambda代入计算,得到不同lambda下训练集和交叉验证集的误差,图6如下所示:
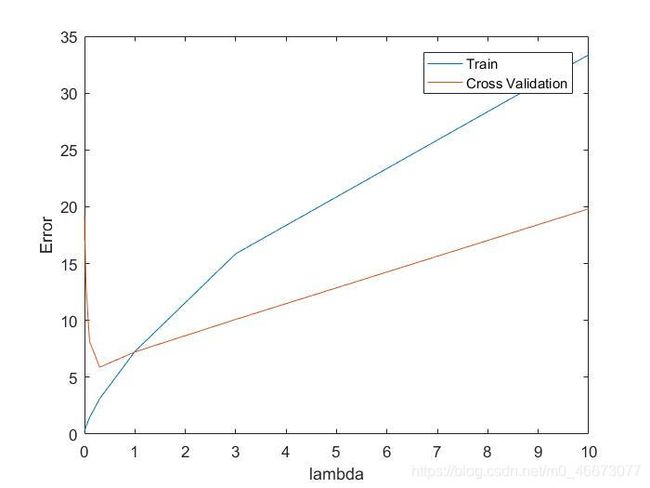
| 图6 λ \lambda λ对代价的影响 |
|---|
可见在lambda=1左右有比较好的表现。观察error_test得到 λ \lambda λ=1时的代价为5.69281951819041,与吴恩达老师题目中得到的lambda=3,代价为3.8599 。目前未找到原因。