吴恩达机器学习(三)线性回归练习
1、单变量线性回归案例(梯度下降法)
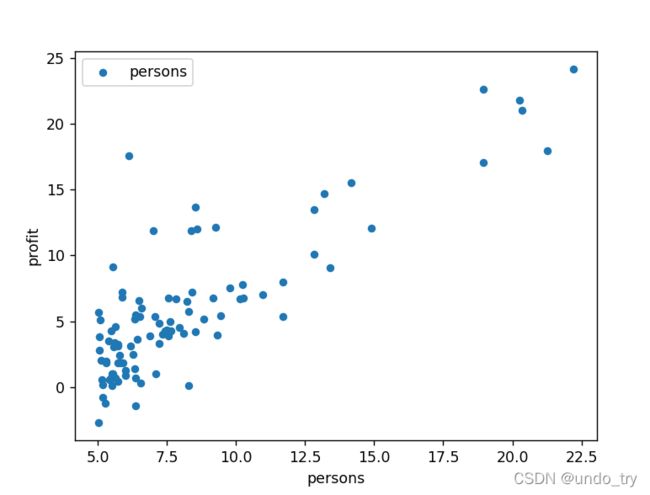
有不同城市对应人口数据 以及 利润,通过城市的人口数据 来预测其利润。
(1)读取数据、并进行可视化
"""
单变量线性回归案例
"""
# 有不同城市对应人口数据 以及 利润
# 通过城市的人口数据 来预测其利润
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 读取数据
df = pd.read_csv('ex1data1.txt',header=None,names=['persons','profit'])
print(df.head())
# 利用pandas进行可视化
df.plot.scatter(x = 'persons', y = 'profit',label = 'persons')
(2)切分出X 和 y
# 在最左边加上一列
ones = df.insert(0,'const',1)
print(df.head())
# 切出X 以及 y
X = df.iloc[:,0:-1]
y = df.iloc[:,-1]
print(X.head())
print(y.head())
# 将X 和 y转换为数组的形式
X = X.values
y = y.values
y = y.reshape(97,1)
print(X.shape)
print(y.shape)
(3)定义代价函数、梯度下降函数、画出J(theta)
# 定义代价函数
def costFunction(X,y,theta):
inner = (X @ theta - y)
return np.sum( np.power(inner, 2) ) / (2 * len(y))
# 计算初始值
theta = np.zeros( (2, 1) )
print(theta)
print(costFunction(X,y,theta))
# 定义梯度下降函数
def gradientDescent(X, y, theta, alpha, iters):
# 保存每一次更新theta后,代价函数的值
costs = []
for i in range(iters):
theta = theta - alpha * X.T @ (X @ theta - y ) / len(y)
cost = costFunction(X,y,theta)
costs.append(cost)
# 打印一些cost值
if i % 100 == 0:
print(cost)
# 循环结束后,返回最终的theta和costs
return theta,costs
# 定义学习率alpha为0.02 迭代的次数iters为2000
alpha = 0.02
iters = 2000
theta,costs = gradientDescent(X,y,theta,alpha,iters)
print(theta)
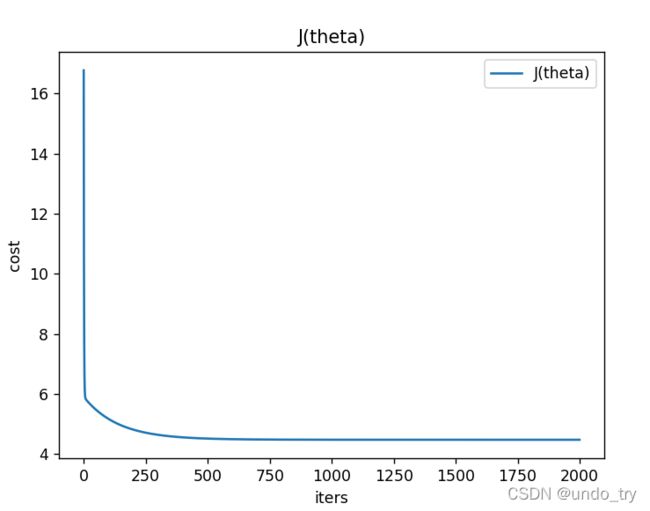
# 画出J(theta)随迭代次数而变化的图
fig , ax = plt.subplots()
ax.plot(np.arange(iters), costs, label = 'J(theta)')
ax.legend()
ax.set(xlabel='iters',ylabel='cost',title='J(theta)')
plt.show()
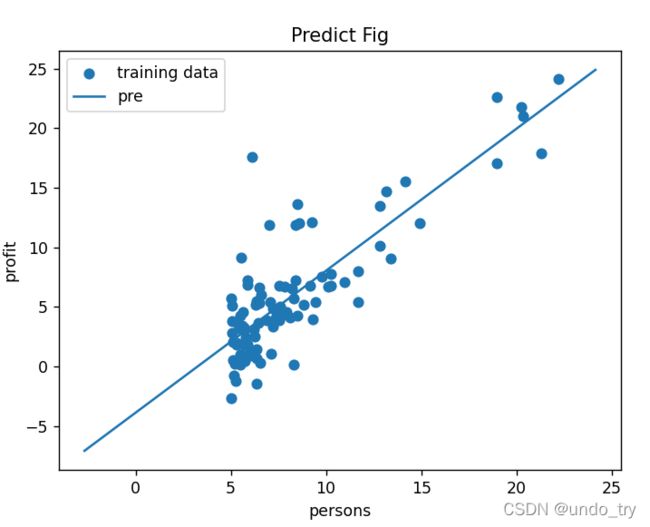
(4) 画出原始数据的散点图 以及 拟合的曲线
# 画出原始数据的散点图
fig , ax = plt.subplots()
ax.scatter(X[:, 1], y, label='training data')
x = np.linspace(y.min(),y.max(), 100)
y_ = theta[0,0] + theta[1,0] * x
print('y_ = ', theta[0,0],' + ', theta[1,0], ' * x')
ax.plot(x, y_, label = 'pre')
ax.legend()
ax.set(xlabel='persons',ylabel='profit',title='Predict Fig')
plt.show()
拟合的曲线为:
y_ = -3.892881498881329 + 1.192742370076755 * x
2、单变量线性回归案例(正规方程)
"""
单变量线性回归案例
"""
# 有不同城市对应人口数据 以及 利润
# 通过城市的人口数据 来预测其利润
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 读取数据
df = pd.read_csv('ex1data1.txt',header=None,names=['persons','profit'])
print(df.head())
# 在最左边加上一列
ones = df.insert(0,'const',1)
print(df.head())
# 切出X 以及 y
X = df.iloc[:,0:-1]
y = df.iloc[:,-1]
print(X.head())
print(y.head())
# 将X 和 y转换为数组的形式
X = X.values
y = y.values
y = y.reshape(97,1)
print(X.shape)
print(y.shape)
# 利用正规方程求出结果
# 正规方程进行求解
def normalEquation(X,y):
return np.linalg.inv(X.T @ X) @ X.T @ y
theta = normalEquation(X,y)
print(theta)
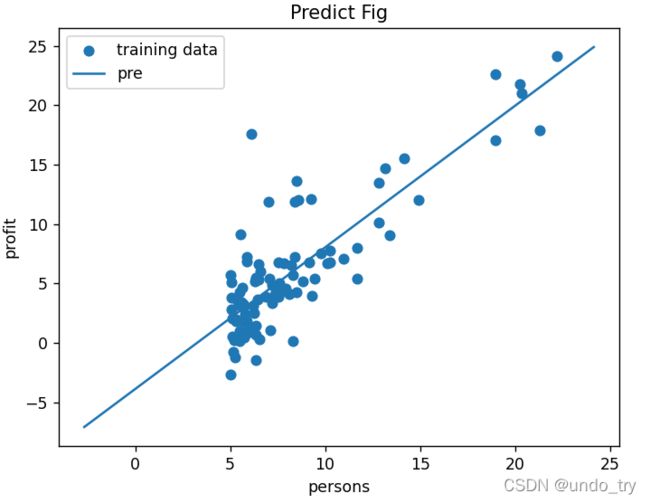
# 画出原始数据的散点图
fig , ax = plt.subplots()
ax.scatter(X[:, 1], y, label='training data')
x = np.linspace(y.min(),y.max(), 100)
y_ = theta[0,0] + theta[1,0] * x
print('y_ = ', theta[0,0],' + ', theta[1,0], ' * x')
ax.plot(x, y_, label = 'pre')
ax.legend()
ax.set(xlabel='persons',ylabel='profit',title='Predict Fig')
plt.show()
拟合的曲线:
y_ = -3.8957808783118772 + 1.1930336441895957 * x
3、多变量线性回归案例(梯度下降法)
通过房子的 面积 以及 卧室的数量 来预测房子的价格
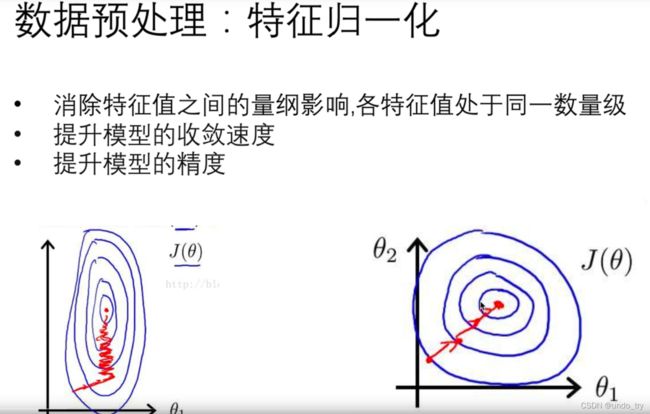
特征归一化的方法举例:

"""
多变量线性回归案例
"""
# 预测房子能卖多少钱???
# 通过房子的 面积 以及 卧室的数量 来预测房子的价格
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 1、读取数据
df = pd.read_csv('ex1data2.txt',header=None,names=['size','bedrooms','price'])
print(df.head())
# size bedrooms price
# 0 2104 3 399900
# 1 1600 3 329900
# 2 2400 3 369000
# 3 1416 2 232000
# 4 3000 4 539900
# 2、因为size的值很大,因此需要做特征归一化
# 定义特征归一化的函数(第一种方法)
def normalization(df):
return ( df - df.mean() ) / df.std()
df = normalization(df)
# 添加一列
df.insert(0,'const',1)
# 切出X 以及 y
X = df.iloc[:,0:-1]
y = df.iloc[:, -1]
# 将X 和 y转换为数组的形式
X = X.values
y = y.values
y = y.reshape(47,1)
print('*****************************')
# 定义代价函数
def costFunction(X,y,theta):
inner = (X @ theta - y)
return np.sum( np.power(inner, 2) ) / (2 * len(y))
# 初始化theta
theta = np.zeros((3,1))
print(theta)
init_cost = costFunction(X,y,theta)
print(init_cost)
# 定义梯度下降函数
def gradientDescent(X, y, theta, alpha, iters):
# 保存每一次更新theta后,代价函数的值
costs = []
for i in range(iters):
theta = theta - alpha * X.T @ (X @ theta - y ) / len(y)
cost = costFunction(X,y,theta)
costs.append(cost)
# 循环结束后,返回最终的theta和costs
return theta,costs
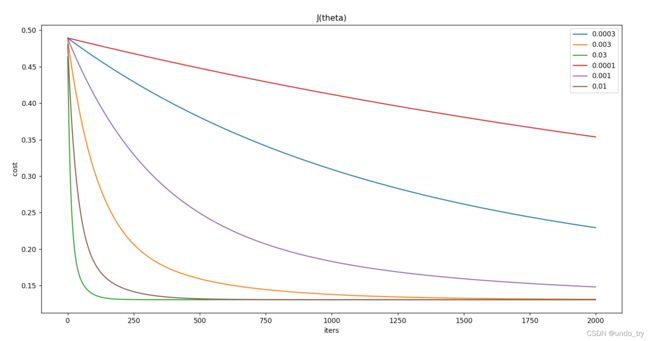
# 比较不同的alpha对J(theta)的影响
alphas = [0.0003, 0.003, 0.03, 0.0001, 0.001 ,0.01]
iters = 2000
# 画出J(theta)随迭代次数而变化的图
fig , ax = plt.subplots()
for alpha in alphas:
theta = np.zeros((3, 1))
theta,costs = gradientDescent(X, y, theta, alpha, iters)
ax.plot(np.arange(iters), costs, label = alpha)
ax.legend()
ax.set(xlabel='iters',ylabel='cost',title='J(theta)')
plt.show()