用小事例来理解模糊控制、人工神经网络、PID控制等

 

自适应控制、预测控制、模糊控制等，跟PID一样，是控制算法。

而粒子群、遗传算法（类似的还有蚁群算法、神经网络，还有机器学习、人工智能中的很多方法）是优化方法，本来跟控制没关系，只不过有时被拿来参数优化，本来就不是为控制器设计而发明的，只不过是在确定了控制框架之后，控制器的设计问题，转为一个优化问题。

1.模糊控制

模糊控制是以模糊集理论、模糊语言变量和模糊逻辑推理为基础的一种智能控制方法，它是从行为上模仿人的模糊推理和决策过程的一种智能控制方法。该方法首先将操作人员或专家经验编成模糊规则，然后将来自传感器的实时信号模糊化，将模糊化后的信号作为模糊规则的输入，完成模糊推理，将推理后得到的输出量加到执行器上。

在这里举一个经典例子：秃子悖论

秃子悖论认为：如果一个有X根头发的人被称为秃子，那么，有X + 1根头发的人也是秃子。所以，(X + 1) + 1根头发的还是秃子。以此类推，无论你有几根头发都是秃子。

关于秃子悖论，有人说，我们可以一般人平均具有的5000根头发为界，规定以下为秃子，以上为不秃。如果这样规定，那么，4999根算不算秃？有5000 根头发的她或他，在梳妆打扮时，梳落了一根，是否当即成为一名“秃子”呢？显然太荒唐！究竟如何解决呢？

数学家们规定，当一个元素完全属于一个集合时，隶属度为 1，反之为0；当一个元素在某种程度上属于一个集合时，它的隶属度为0~1之间的某个值（这种取值范围类似概率）。那么，对于这个悖论，我们可以约定，稀稀落落的500根头发以下者为完全秃头，它对于{秃子}这个集合的隶属度为1，而5000根以上的头发茂密者为完全不秃头，他对于{秃子}集合的隶属度为0。这样，501-4999根头发者就在某种程度上属于{秃子}集合。如501根者，隶属度为0.998，而4999根者，隶属度为 0.002。这就是说，501～49999根者对于{秃子}集合是一种“既属于又不属于”的状态。这样，应用模糊数学，我们很好地解决了秃子悖论。

   

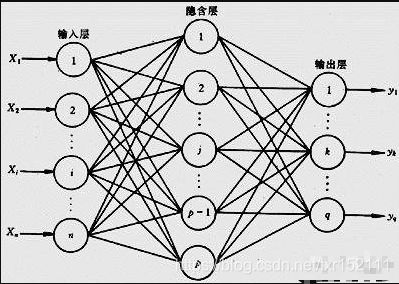
2. 人工神经网络

人工神经网络的灵感来自其生物学对应物。大脑的许多功能仍然是个谜，但是我们知道的是，生物神经网络使大脑能够以复杂的方式处理大量信息。

神经网络是一种运算模型，由大量的节点（或称神经元）之间相互联接构成。每个节点代表一种特定的输出函数，称为激励函数（activation function）。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重，这相当于人工神经网络的记忆。网络的输出则依网络的连接方式，权重值和激励函数的不同而不同。

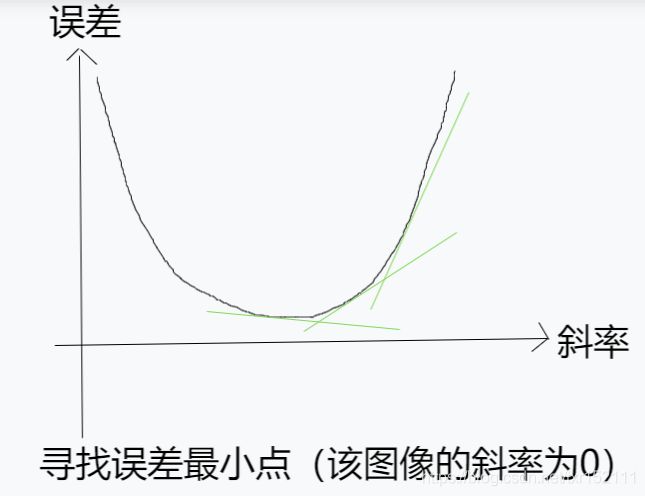
神经网络的学习，就是根据误差来调整参数。从最简单的例子讲起，其实就是一个猜数字游戏：需要得到的值就是我写下的一个值，然后你进行猜数:

A：“5?”

B："猜小了"

A："7？"

B：“猜大了”

A：“6？”

B：“猜对了！”

人对数据的处理可以进行倒推，但是计算机却不是这样，计算机有强大的计算能力，却没有思维能力（所以有时候会瞎算出一些奇怪的东西）。比例，我买了3斤糖果花21块钱，那么1斤糖果多少钱？计算机先猜个数，比如先猜1块钱1斤，那么3斤就是3块钱，和已知的3斤糖果花21块钱相比明显小了；那我增大再猜1块钱5斤，3斤是15块钱，和已知的3斤糖果花21块钱还是小了；再增大一块钱10斤，3斤30元，猜大了，那再逐渐减小，最终猜到一块钱是7斤。这个简单的例子就是神经网络的学习过程。

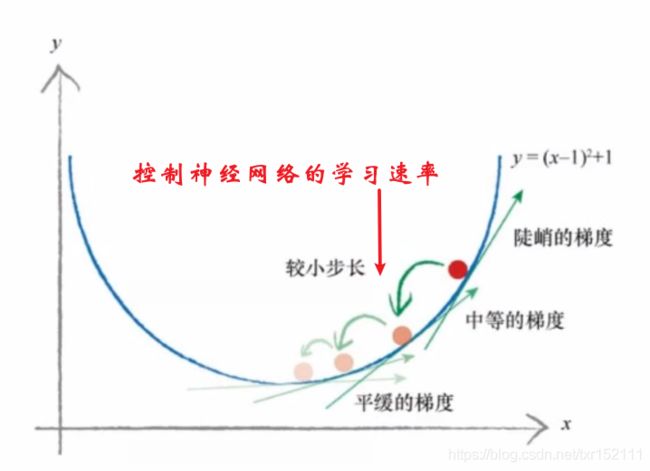
再取个复杂点的问题：一种毛毛虫，厚度和长度可能存在某个比例关系。取一些样本的数据，横纵坐标分别为长度和厚度，关键是求出斜率的值，这就像前面的猜数字游戏猜（suan）出来斜率，根据每次猜的数所在的误差来调整猜的斜率。为了控制不要太跑偏了，会控制增加或减少的值，防止出现第一次猜15，发现小了，结果下一次猜50，发现大了，下次再猜10，又是小了，这样可能永远得不到正确的值，控制的叫做“神经网络的学习速率”，这个过程就是训练的过程。神经网络的学习，就是根据误差来调整参数。

 这是对简单的一层，多层其实也是简单的一层层嵌套。例如如何区分两种毛毛虫。可能根据数据画出三条线来进行处理：

基于基本的原理得出了很多神经网络模型，可查阅：

一文看懂25个神经网络模型

科普主流的神经网络模型及应用场景

 3.  PID控制

 PID( Proportional Integral Derivative，比例   积分  微分)控制是最早发展起来的控制策略之一，由于其算法简单、鲁棒性好和可靠性高，被广泛应用于工业过程控制，尤其适用于可建立精确数学模型的确定性控制系统。任何闭环控制系统的首要任务是要稳（稳定）、快（快速）、准（准确）的响应命令。PID调整的主要工作就是如何实现这一任务。

P—比例控制系统的响应快速性，快速作用于输出，好比"现在"（现在就起作用，快），I—积分控制系统的准确性，消除过去的累积误差，好比"过去"（清除过去积怨，回到准确轨道），D—微分控制系统的稳定性，具有超前控制作用，好比"未来"（放眼未来，未雨绸缪，稳定才能发展）。当然这个结论也不可一概而论，只是想让初学者更加快速的理解PID的作用。

比例控制可快速、及时、按比例调节偏差，提高控制灵敏度，但有静差，控制精度低。

积分控制能消除偏差，提高控制精度、改善稳态性能，但易引起震荡，造成超调。

微分控制是一种超前控制，能调节系统速度、减小超调量、提高稳定性，但其时间常数过大会引入干扰、系统冲击大，过小则调节周期长、效果不显著。

比例、积分、微分控制相互配合，合理选择PID调节器的参数，即比例系数KP、积分时间常数τi和微分时间常数τD，可迅速、准确、平稳的消除偏差，达到良好的控制效果。

PID控制的缺点：1. 在实际工业生产过程往往具有非线性、时变不确定，难以建立精确的数学模型，常规的PID控制器不能达到理想的控制效果；2. 在实际生产现场中，由于受到参数整定方法烦杂的困扰，常规PID控制器参数往往整定不良、效果欠佳，对运行工况的适应能力很差。

具体的数学原理可参考：PID控制原理

小明接到这样一个任务：有一个水缸漏水，且漏水的速度是不定的，但要求水面高度维持在某个位置，一旦发现水面高度低于要求位置，就要往水缸里加水。

开始小明用瓢加水，水龙头离水缸有十几米的距离，经常要跑好几趟才加够水，于是小明又改为用桶加，一加就是一桶，跑的次数少了，加水的速度也快了，但好几次将缸给加溢出了，不小心弄湿了几次鞋，小明又动脑筋，我不用瓢也不用桶，老子用盆，几次下来，发现刚刚好，不用跑太多次，也不会让水溢出。这个加水工具的大小就称为比例系数。

小明又发现水虽然不会加过量溢出了，有时会高过要求位置比较多，还是有打湿鞋的危险。他又想了个办法，在水缸上装一个漏斗，每次加水不直接倒进水缸，而是倒进漏斗让它慢慢加。这样溢出的问题解决了，但加水的速度又慢了，有时还赶不上漏水的速度。于是他试着变换不同大小口径的漏斗来控制加水的速度，最后终于找到了满意的漏斗。漏斗的时间就称为积分时间。

小明终于喘了一口，但任务的要求突然严了，水位控制的及时性要求大大提高，一旦水位过低，必须立即将水加到要求位置，而且不能高出太多，否则不给工钱。小明又为难了！于是他又开努脑筋，终于让它想到一个办法，常放一盆备用水在旁边，一发现水位低了，不经过漏斗就是一盆水下去，这样及时性是保证了，但水位有时会高多了。他又在要求水面位置上面一点将水凿一孔，再接一根管子到下面的备用桶里这样多出的水会从上面的孔里漏出来。这个水漏出的快慢就称为微分时间。

故事中小明的试验是一步步独立做，但实际加水工具、漏斗口径、溢水孔的大小同时都会影响加水的速度，水位超调量的大小，做了后面的实验后，往往还要修改改前面实验的结果。

当被控对象的结构和参数不能完全掌握，或得不到精确的数学模型时，控制理论的其它技术难以采用时，系统控制器的结构和参数必须依靠经验和现场调试来确定，这时应用PID控制技术最为方便。即当我们不完全了解一个系统和被控对象﹐或不能通过有效的测量手段来获得系统参数时，最适合用PID控制技术。PID控制，实际中也有PI和PD控制。PID控制器就是根据系统的误差，利用比例、积分、微分计算出控制量进行控制的。

4. 鲁棒控制和自适应控制

鲁棒控制是以目的定义的控制方法集合；自适应控制是以手段定义的控制方法集合。

这两种控制都是为了应对 “当数学模型不能精确表示实际系统的情况下，传统基于模型的控制该如何做？” 这个大问题的。

狭义的鲁棒控制是指H2，Hinf，LMI等控制，主要思想是使控制器对模型不确定性(外界扰动，参数扰动)灵敏度最小来保持系统的原有性能。
广义的鲁棒控制则是指所有用确定的控制器来应对包含不确定性的系统的控制算法，所以研究滑模控制，自适应控制，包含学习、辨识等算法的智能控制也可以算作鲁棒控制。

而自适应控制则是指通过在线调整控制器参数来应对系统不确定性的控制算法。这是一种很好的应对不确定性的手段，所以现在很多控制器研究中都经常利用到自适应的思想，而这些控制器往往会因此而具有较强的鲁棒性。