2020_ACM MM_MISA: Modality-Invariant and -Specific Representations for Multimodal Sentiment Analysis

MISA: Modality-Invariant and -Specific Representations for Multimodal Sentiment Analysis

论文地址：https://dl.acm.org/doi/abs/10.1145/3394171.3413678?casa_token=oI8VnZ8Eg10AAAAA:mVUbDA0AZiAXcDxiDmV9-ooRH4PxzlSMXkBCgm1OCopziDWz8U3ZU54VzJIfqCCsbRFAvk8_kJhzBQ

简介

解决多模态情感分析任务的一个主要方法是开发一个复杂的融合技术，在多模态情感分析任务中，尽管基于注意力的模型和基于张量融合等方法都取得了一些进展，但是这些融合技术会受到不同模态存在模态鸿沟的挑战。

为了能够学习互补的信息以尽量减少冗余(引入了模态不变空间)并纳入多样化的信息集(引入了模态特定的空间)，并学习捕获这些理想特性的潜在模态表征以帮助多模态的融合，本文提出了MISA模型，它能够通过学习有效地模态表征来辅助特征融合过程。该模型学习每个模态的分解子空间，以获得更好的模态表征用于融合的输入。MISA为每种模态学习了两种不同的表示空间：

• 第一个表示空间是模态不变的(Modality-Invariant)，学习不同模态表征之间的共性并减少模态差距。虽然多模态信号来自不同的模态，但是这些不同的模态有着共同的动机和说话者的目标。不变映射有助于捕获做这些潜在地共性和相关的特征，作为共享子空间上的对齐投影。
• 第二个表示空间是模态特定的(Modality-Specific)，该空间是每一种模态所特有的，并学习模态特有的特征。对于任何信息，每种模态都有自己独特的特征，包括说话者的表达风格信息，这种特异性的细节往往与其他模态不相关，被称为噪音。但是这种噪音在预测情感状态是非常有用的，例如说话者倾向于讽刺的表达方式，就偏重于极端情感的表达。

学习模态特定的特征和不变空间中捕获的共同潜在特征，可以提供一个全面的多模态语料表征，并使用这个完整的表征进行融合，然后用于分类任务。

为了学习模态不变和模态特定的两个子空间，需要结合各种损失：

• 分布相似性损失(distributional similarity loss)：用于不变特征。
• 正交损失(orthogonal loss)：针对特定特征。
• 重建损失(reconstruction loss)：针对具有代表性的模态特征。
• 任务预测损失(task prediction)：用于最终的分类预测任务。

MISA

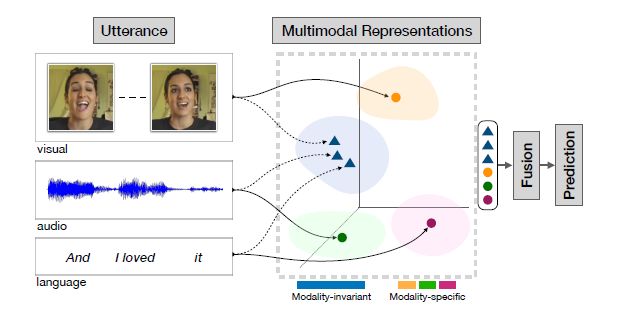
MISA框架的整体结构主要包括两个阶段：模态表征学习和模态融合。

下图为MISA框架的完整结构，首先对文本、视频、音频三种信息进行特征提取，然后学习不同模态不同子空间下的模态表征，最后对这些模态表征进行融合并使用transformer对融合的信息进行处理，以用于最终的分类任务。

数据中的每个视频被分割成一个个小视频(语料)作为模型的输入。对于一个语句(可以理解为一段视频的长度，它包含文本，音频，视频信息)$U$，输入包括语言$(l)$、视觉$(v)$、音频$(a)$三个低层次的特征序列。三个序列分别表示为$U_l\in R^{T_l\times d_l},U_v\in R^{T_v\times d_v}$和$U_a\in R^{T_a\times d_a}$，这里$T_m$表示话语的长度(由多少个语料组成)，$d_m$表示每个模态各自的特征维度。

我们的任务是利用这些序列$U_m\in \{l,v,a\}$来预测该语句$U$所表达的情感取向。

1、特征提取

对于每个模态$m\in l,v,a$，首先将使用堆叠的双向长短时记忆(LSTM)提取语料序列$U_m\in R^{T_m\times d_m}$的特征，然后后面在加上全连接的密集层，将其映射到固定大小的向量

$u_m\in R^{d_h}$，其计算公式为：
$$u_m=sLSTM(U_m;{\theta }_m^{lstm})\text{\hspace{1em}(1)}$$

1. 公式中只体现了堆叠的双向长短时记忆，其后面应该有线性层才能得到最终的固定大小的特征向量$u_m$(对于每个模态，特征向量的长度是相同的)。

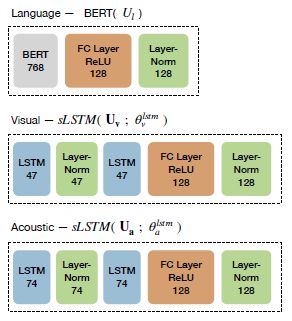
2. 其中对于音频和视频模态只是用sLSTM进行特征提取；而对于文本模态，可以使用sLSTM也可以使用BERT，由上图可知是使用的BERT(虽然公式中把文本写成与视频和音频使用的是一样的了)。在代码中也是可以选择的，当然使用BERT的效果肯定要好了哇。

下图为所使用的BERT和sLSTM的结构，并在后面添加了线性层使得每个模态的特征向量是一样大小的。对于不同数据集其模型中参数大小是不同的，但是结构是一样的，在此以MOSI数据集为例(后面所用到的的结构也以MOSI为例)。

2、模态表征-模态不变和模态特定表征(Modality-Invariant and -Specific Representations)

将每个模态的特征向量(这里应该是一句完整各模态的特征向量)投影到两个不同的表示空间中。

第一个是模态不变组件(空间)，它在具有相似性约束的公共子空间中学习共享表示。这种约束有助于最小化不同模态之间的异质性，有助于多模态融合。实际的操作就是就是使用具有相同权重的线性网络去处理不同的模态。

第二个是针对模态特定的部分，捕获每一个模态的独特特征。

在本文中，模态不变和模态特定的表征为有效的特征融合提供了完整的多模态表征。学习这些表征是本文的首要目标。

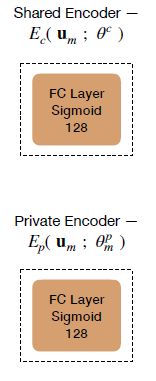
对于模态m的特征向量$u_m$，使用编码函数学习隐藏的模态不变($h_m^c\in R^{d_h}$)和模态特定($h_m^p\in R^{d_h}$)表征：
$$h_m^c=E_c(u_m;{\theta }^c),h_m^p=E_p(u_m;{\theta }_m^p)\text{\hspace{1em}(2)}$$
三个模态经过两个编码函数一共生成了六个隐藏向量。其中两个编码函数都是简单的线性神经网络：$E_c$在三种模态下共享同一个参数${\theta }^c$(也就是说三个模态使用同一个神经网络来学习模态不变表征)，而$E_p$为每种模态分配单独的参数${\theta }_m^p$(三个模态使用三个不同的神经网络来学习模态特定表征)。下面为这两种(准确来说是四种)线性网络的结构。

可以看到其都是一层线性网络，对于模态表征共享同一组参数；对于模态特定标号只能使用不同的参数：

3、模态融合&预测

将每个模态投影到各自的表征中后，需要将它们融合进一个联合的向量中。本文的融合机制为，先对表征向量(每个模态两个，共六个)使用Transformer进行自我关注，然后对这六个经过transformer的模态向量进行拼接，用于最终的情感预测。

下面看看transformer是如何进行工作的:

Transformer使用了自注意力模块，该模态通过使用一个缩放的点积实现自注意力的计算：
$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_h}})V\text{\hspace{1em}(3)}$$
其中Q、K和分别为查询、键和值矩阵，它们是由同一个输入经过三个不同的权重矩阵得到的。在Transformer中，计算了多个这样的注意力(称为多头注意力)，其中第$i$个头的计算方法为:
$$hea{d}_i=Attention(Q{W}_i^q,K{W}_i^k,V{W}_i^v)\text{\hspace{1em}(4)}$$
$W_i^{q/k/v}\in R^{d_h\times d_h}$是每个头特有的参数，在经过多头注意计算之后，会与输入进行残差连接并使用$LayerNorm$层处理得到多头注意力层的输出。然后再经过MLP层,同样使用了残差连接和$LayerNorm$层处理。就得到了最终的Transformer编码器的输出，本文只使用Transformer编码器对模态向量进行自注意力的计算。

然后我们再来看看是如何进行模态融合的：

将模态不变和模态特定的编码函数(公式2)的六个模态表征输出堆叠成一个矩阵$M=[h_l^c,h_v^c,h_a^c,h_l^p,h_v^p,h_a^p]\in R^{6\times d_h}$，然后会用transformer对这些表征进行多头自注意力的计算，使每个向量都学习到其他向量的跨模态表征。这样可以使得每个表征从其他表征中诱导出潜在地信息，这些信息对整体的情感预测有协同作用。

对于输入矩阵$M$，在经过Transformer计算之后，得到一个新的矩阵$\overline{M}=[{\overline{h}}_l^c,{\overline{h}}_v^c,{\overline{h}}_a^c,{\overline{h}}_l^p,{\overline{h}}_v^p,{\overline{h}}_a^p]$，其计算过程为：
$$\overline{M}=MultiHead(M;{\theta }^{att})=(hea{d}_1\oplus \cdots hea{d}_n)W^o\text{\hspace{1em}(5)}$$
其中${\theta }^{att}=\{W^q,W^k,W^v,W^o\}$为多头注意力计算的参数，$\oplus$代表连接。

这里应该还有残差连接、层归一化和多层感知机才能得到Transformer的最终输出，可能是因为多头注意力是Transformer的核心，所以只介绍了这一部分。

预测和推理

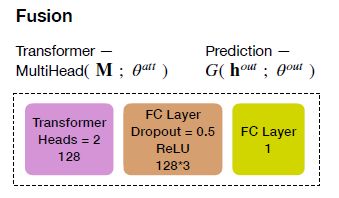
将Transformer得到的矩阵，将其展开拼接成一个向量$h^{out}=[{\overline{h}}_l^c\oplus \cdots {\overline{h}}_a^p]$，然后使用函数$\hat{y}=G(h^{out};{\theta }^{out})$对拼接后的向量进行处理得到最终的预测结果。其中函数$\hat{y}=G(h^{out};{\theta }^{out})$是一个线性网络，它和transformer的拓扑结构如下图所示：

4、学习

在上面我们介绍了将每个模态分别投影到两个不同的子空间，分别学习其模态不变和模态特定的表征。那怎么进行学习呀？如果只使用预测时的损失函数是肯定做不到的哇，那么就需要使用其他的损失函数来学习到这些模态不变和模态特定的表征，下面就来看看这些损失函数吧。

在本文中，使用了四种损失函数，分别为Similarity Loss${\mathcal{L}}_{sim}$、Difference Loss${\mathcal{L}}_{diff}$、Reconstruction Loss${\mathcal{L}}_{recon}$和task Loss${\mathcal{L}}_{task}$。最终将这些损失函数进行组合作为整体的损失函数，通过最小化整体的损失函数来学习模型：
$$\mathcal{L}={\mathcal{L}}_{task}+\alpha {\mathcal{L}}_{sim}+\beta {\mathcal{L}}_{diff}+\gamma {\mathcal{L}}_{recon}\text{\hspace{1em}(6)}$$
其中$\alpha ,\beta ,\gamma$是每个损失对总损失$\mathcal{L}$的共享的权重值。

下面看看这些损失函数是如何实现将每个模态投影到预期的子空间并学习到模态不变和模态特定表征的。

${\mathcal{L}}_{sim}$-Similarity Loss

相似性损失用于学习每个模态的模态不变表征。最小化相似性损失可以减少每种模态的共享表征之间的差异。有助于共同的跨模态特征在共享子空间(模态不变空间)中对其。我感觉是为了学习每种模态中一些相同的特性。

本文使用中心距差异(CMD)作为相似性损失。CMD是一种先进的距离度量，它通过匹配两个表示的阶数钜差来衡量两个表示的分布之间的差异。直观上看，CMD距离会随着两个分布变得更加相似而减少。

设$X$和$Y$是有界的随机样本，在区间$[a,b{]}^N$上的概率分布为$p$和$q$。中心钜差异正则$CM{D}_k$被定义为$CMD$度量的经验估计，即：
$$CM{D}_K(X,Y)=\frac{1}{|b-a|}||E(X)-E(Y)|{|}_2+\sum _{k=2}^K\frac{1}{|b-a{|}^k}||C_k(X)-C_k(Y)|{|}_2\text{\hspace{1em}(7)}$$
其中，$E(X)=\frac{1}{|X|}{\sum }_{x\in X^x}$是样本$X$的经验期望向量。$C_k(X)=E((x-E(X){)}^k)$是所有$k^{th}$阶样本的中心钜的向量，即$X$的坐标。

在本文中，计算每对模态不变表示之间的CMD损失：
$${\mathcal{L}}_{sim}=\frac{1}{3}\sum _{(m_1,m_2)\in \{(l,a),(l,v),(a,v)\}}CM{D}_K(h_{m_1}^c,h_{m_2}^c)\text{\hspace{1em}(8)}$$
在这里也可以选择其他损失函数，比如KL散度、MMD或对抗性损失，是因为CMD他足够简单并且效果足够好。

${\mathcal{L}}_{diff}$-Difference Loss.

该损失是为了确保模态不变和模态特定表征捕获输入的不同方面。这种非冗余性(不同特征)的学习主要通过在两个表征之间使用软正交约束来实现。设$H_m^c$和$H_m^p$为二维矩阵，它的每一行代表模态$m$每个话语的特征向量$h_m^c$和$h_m^p$，分别来自不同的表示空间。该模态的正交性约束被计算为：
$$||H_m^{c^{\top }}{H}_m^p|{|}_F^2\text{\hspace{1em}(9)}$$
其中$||.|{|}_F^2$是Frobenius范数的平方。除了模态不变向量和模态特定向量之间的约束外，还增加了模态特定向量之间的正交性约束，因此为了获得更多不同方面的信息，所使用的损失函数为：
$${\mathcal{L}}_{diff}=\sum _{m\in \{l.v,a\}}||H_m^{c^T}{H}_m^p|{|}_F^2+\sum _{(m_1,m_2)\in \{(l,a),(l,v),(a,v)\}}||H_{m_1}^{p^T}{H}_{m_2}^p|{|}_F^2\text{\hspace{1em}(10)}$$
损失函数是成对计算的，因此需要对六对表征向量计算正交性约束，六对损失的和即为最终的Difference Loss。

正交化的概念是指，你可以想出一个维度，这个维度你想做的是控制转向角，还有另一个维度来控制你的速度，那么你就需要一个旋钮尽量只控制转向角，另一个旋钮，只控制速度。如果有一个旋钮既可以控制转向角和速度，那么控制起来就很困难。

下面是我自己的理解。。。

这里提到的正交，就是不同模态去学习不同的特性。就比如模态A控制特性1，模态B控制特性2，假如特性1对于情感的预测比较好，那么就用模态A控制特性1表达的更强烈一点，就不需要模态B去控制特性1，即每种模态学习特定的性质就好了，那种共有的特性就不用在学习了。应该是这样吧。。。

${\mathcal{L}}_{recon}$-Reconstruction Loss.

由于Difference Loss的使用，模态特定的编码器$E_p$可能会学习到一些比较琐碎(应该是不重要的吧)表征。如果编码器函数生成不同模态特征向量是正交的但是又不是很重要(对于情感预测不是很重要)的向量，那么学到的这种特征就比较平凡了(就是学到的特征太多了，学到了一些跟情感预测没啥关系的特征)。

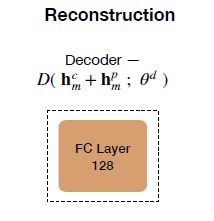
为了避免上述的情况，添加了一个重构损失，确保学习到的隐藏的表征能够捕捉到他们各自模态的细节（我觉得是为了避免学习到一些乱七八糟的表征）。

具体的操作是：把每一个模态经过两个子空间(模态不变和模态特定)后的输出相加然后传入线性层就得到了每一个模态的重构模态即${\hat{u}}_m=D(h_m^c+h_m^p;{\theta }^d)$，而重构损失就是重构后的模态向量${\hat{u}}_m$与重构之前的模态向量$u_m$之间的均方误差损失：
$${\mathcal{L}}_{recon}=\frac{1}{3}(\sum _{m\in \{l.v,a\}}\frac{||u_m-{\hat{u}}_m|{|}_2^2}{d_h})\text{\hspace{1em}(11)}$$
其中，$||.|{|}_2^2$是$L_2$范数的平方。

个人理解：是为了避免各模态在经过线性操作后 的特征向量与之前的特征向量差距过大，以学习到一些不重要的特征。

获得重构模态的编码器函数的结构如下图所示：

${\mathcal{L}}_{task}$-task Loss.

任务损失估计了训练期间预测的质量，就是评价预测和真实标签之间的差距，就是经常使用的一类损失函数。对于分类任务，使用交叉熵损失函数；对于回归任务，使用均方误差损失函数。对于一个批次，其计算方式为：
$$\begin{gathered} {\mathcal{L}}_{task}=-\frac{1}{N_b}\sum _{i=0}^{N_b}{y}_i\cdot log{\hat{y}}_{i}forclassification \\ =\frac{1}{N_b}\sum _{i=0}^{N_b}||y_i-{\hat{y}}_i|{|}_2^{2}forregression\text{\hspace{1em}(12)} \end{gathered}$$

感觉选择合适的损失函数对预测的结果还挺有帮助的。

特征提取

对于文本：使用BERT；对于视频：CMU-MOSI和CMU-MOSEI使用Facet提取面部表情特征，UR_FUNNY使用OpenFace，然后再使用LSTM；对于音频：使用COVAREP，然后使用LSTM。

数据集

说一下数据集，这里除了使用了常用的CMU-MOSI和CMU-MOSEI数据集，还用了UR_FUNNY数据集，它是一种多模态幽默检测数据集。与情感类似，产生和感知幽默也是通过多模态渠道进行的。数据集使用TED演讲中抽取的笑料，并提供了多模态语料，每个语料都被贴上了幽默/非幽默的二元标签。

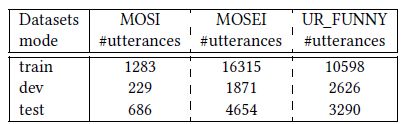
三个数据集的大小由下表所示：

实验

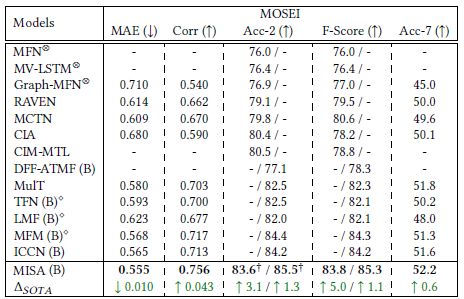
MOSI数据集上：

MOSEI数据集上：

UR_FUNNY数据集上：

代码的流程：