深度学习图像分类（一）：LeNet

深度学习图像分类（一）：LeNet

---

---

前言

LeNet5诞生于1994年，是最早的卷积神经网络之一， 由Yann LeCun完成，推动了深度学习领域的发展。在那时候，没有GPU帮助训练模型，甚至CPU的速度也很慢，因此，LeNet5通过巧妙的设计，利用卷积、参数共享、池化等操作提取特征，避免了大量的计算成本，最后再使用全连接神经网络进行分类识别，这个网络也是最近大量神经网络架构的起点，给这个领域带来了许多灵感。

---

一、卷积神经网络

首先，要讲LeNet，卷积神经网络是大家必须掌握的前置知识。
在讲卷积之前，我们先来了解一下什么是核：

1、核概念：

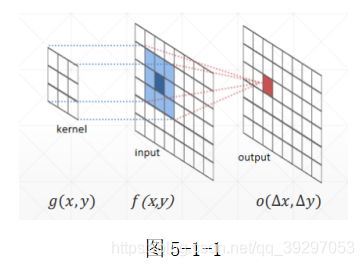
如图5-1-1：g（x,y）即为核，每个小方格上都有一个标量代表权重w。f(x,y)为输入，每个小方格上都有一个标量代表该图片在该点上的像素值。卷积的定义是两个变量在某个范围内相乘后求和是结果。对应图中就是让核与输入两个平面平行对应，每个对应点进行相乘后求和，得到的值作为输出。
核概念早在计算机视觉中得以应用，通过设定不同的核大小及权值可以实现对图片的处理，如图片锐化，图片模糊化，图片边缘化等等。

深度学习中的核概念不同与计算机视觉中不同的一点为：在计算机视觉中用于处理图片的不同核大小可能是通过经验得来的。而深度学习中核的权值大小是模型自己学习总结出的。

2、卷积的理解

众所周知，在全连接神经网络中，全连接神经网络随着隐藏层和隐藏节点的增加，参数的增加量是十分巨大的。正是因为这些大量的参数，使得神经网络模型有着极强的学习能力，但是也造成了计算的困难。

卷积神经网络的发明很好是解决了这一问题。为了很好的了解卷积的概念，我们可以先从生物学的角度进行理解。

当我们欣赏一幅图片的时候，大概有两种欣赏方式。其一是纵观全局，这便相当与全连接神经网络方式；其二是关注局部，然后保证观察角度不变，进行上下左右平移，来观察整张图片，这便相当于卷积神经网络。如图图5-1-2：

每个圆圈可理解为隐藏层的结点，连线的角度可以抽象成权值W，连线所在图片中的对应点的像素值为X，加上偏置即为WX+b模型。当以全连接层方式观察时，每变换一个结点，相当于变换一个观察角度，所有的连线角度都会改变，造成了所有的W都不一样，所以全连接层的参数会很多。反观卷积层方式，当选定一个核（后面解释，即图中彩色长方形区域）大小时，变换每个结点时，通过核的上下左右移动来遍历整张图片，在此过程中，连线的角度不变，即权值的大小不变，由次可以解释卷积方式参数大量下降的原理。

3、步幅与填充

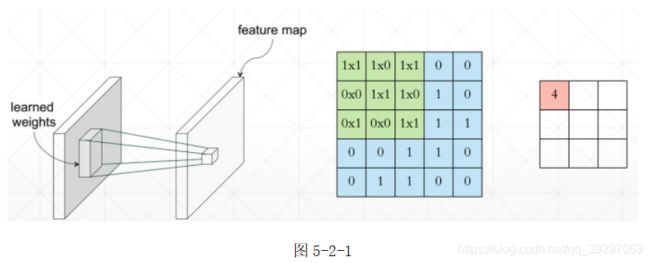
经过对卷积方式和核概念的认识，我们可以将卷积神经网络理解为一个核在输入图片上遍历的过程，遍历过程中核与输入之间的对应点的乘积求和即为输出。卷积神经网络模型的更新依然可以根据loss的梯度下降法和参数的反向传播来进行，由于之前梯度下降和反向传播的介绍，这里不做重复的推导。因为核是一个矩阵，其存在大小，所有经过卷积操作后的输入维度总是略小于输入维度。例如图所示，一个5×5的单通道输入，经过一个3×3大小的核映射，得到的输出维度为3×3。如图5-2-1所示：

很多情况下，我们希望得到是输出与输入的大小格式保持一致，此时需要在输入的四周填充一圈空白，使核遍历图片后得到的映射输出大小不变。填充的空白大小与核的大小成正相关。步幅的作用是用来降维的，如图：当步幅为1时，将一个5×5的输入填充成6×6，再经过一个3×3的核映射，其输出维度不变。若此时将步幅调整为2，则只能得到一个3×3是输出维度。如图5-2-2所示：

4、通道：

一般来说，我们会将一个图片抽象为四维[数量，长，宽，色彩]。例如对于一张32X32像素的彩色照片来讲，我们一般将其抽象为向量[1,32,32,3], 最后的3指的是RGB三个颜色通道，所以卷积核的维度是[kernel_H , kernel_W，3] ，对应下图的彩色图片上的三个矩形框。经过卷积操作后，我们会对应得到3个特征分布（feature map），然后将3个特征分布的对应位置融合，最后得到一个特征图的输出，如图5-2-3：

除此之外，为了保证模型的学习能力，我们一般会从多个观察角度对图片进行观察，即取不同的核，如图5-2-4，我们对一张32X32像素的彩色照片取四个核进行映射（四个不同的观察角度，每个卷积核期望学习到图像中的不同特征），得到的输出格式是一个向量[1,30,30,4]

输入[1,32,32,3]：代表数量为1，大小为32*32，色彩通道为3。

核[4,3,5,5]：代表4个不同的核，每个核映射出来的特征分布有3个分别对应3个不同的色彩通道，核的大小为5*5。

输出[1,30,30,4]：一般来说我们将3个色彩通道的像素值相加，即将3降维为1，输出大小为30*30，因为这里没有扩充边界，所以输出维度略小于输入维度。通道4解释为因为有4个核所以对应4个不同输出。

这里要明确的是，每一次卷积的维度变化，假设：
输入的feature maps的维度是 [1, 32, 32, 3]，卷积核的维度是 [kernel_H , kernel_W，3]
那么每一个卷积核对于输入feature maps的处理都是将维度从[1, 32, 32, 3]变成[1, 30, 30, 1]。
最后，由于我们有4个不同的卷积核，将四个 [1, 30, 30, 1] 拼到一起才得到维度 [1, 32, 32, 4]。

5、池化与采样

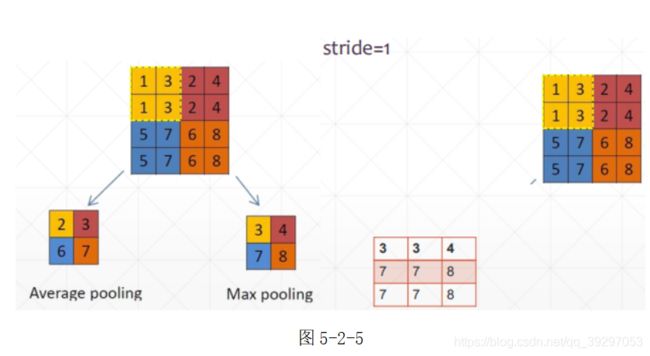
池化的主要用途是在保证原始特征信息的同时，进行特征的降维，压缩数据和减少参数。在一定程度上可以减轻过拟合现象，同时提高模型的容错性。比如以（3，3）作为一个池化单位，其含义就是每次将33=9个特征值根据池化算法合并成一个特征值。采样方式分为上采样和下采样。常用的下采样池化算法有Average pooling和Max pooling。如图，当步长为2时，可以将一个44的特征分布（feature map）下采样为22的特征分布。当步长为1时，则会得到一个33的特征分布。即，下采样后的特征大小与池化的大小和步长有关。如图5-2-5：

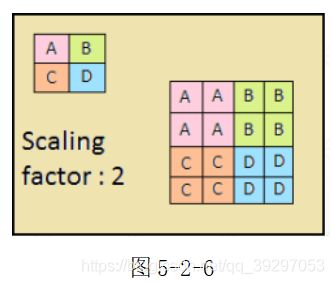
上采用比较简单易理解，可以起到将信息等比放大的作用，放大的倍数与池化的大小有关。如5-2-6图将信息等比放大两倍。

6，卷积神经网络的意义

卷积神经网络在图片识别上意义重大，它的意义远不止减少参数量这一点。实际上，对图片进行卷积操作就是把卷积模板（核）与原图片做点积操作。点积的数学解释可以解释为：两个向量之间的相似度。推广到这里，可以说成核与原图的相似度，卷积的结果越小，说明图片中某位置和核的相似度越小，反之亦然。如何把核作为特征算子或者特征向量，那么卷积的过程就是通过移动核在原图中的对应位置，不断去寻找是否有一部分是符合我这个特征向量的，这在图片识别中意义重大。

对图片是识别实际上就是对底层特征的不断提取。打个比方，我们判断一张图片是否为车子，它的底层特征为像素。假设我们的卷积模型设置了10个核，它们的特征可能代表[颜色，形状，轱辘，车窗，方向盘，人…]等待，通过核在原图上进行匹配进而综合判断该图片是否为车子。

实际上，深度卷积神经网络就是去求解这千千万万个核的这么一种网络。这些核不是凭借我们的经验随便定义的，而是通过不断的学习更新得来的，深度卷积神经网络就是不断地去学习，最终求得这些核。而神经网络的不易解释性就在于此，随着模型的复杂，抽象出的核千千万万，我们难以去解释每个核的具体含义，也难以介绍每个中间层和中间结点的含义。

7，小结

总的来说，对于图像分类任务。卷积神经网络层级结构可大致分为五个结构，分别为输入层，卷积层，激励层，池化层和全连接层。

输入层：与传统的神经网络模型一样，模型的输入需要进行预处理操作，常见的预处理操作有：去均值，归一化，图像增广，规范图像尺寸等等。

卷积层：生物角度解释其作用就是----局部感知：人的大脑在识别图片的过程中，并不是一下子识别一整张图片的，而是对图片中的每个局部特征进行有顺序的局部识别，不断提取底层信息抽象出高层特征，然后更高层次对局部进行综合操作，从而得到全局信息。

激励层，本质就是激活函数，对卷积层的输出结果做一个非线性映射，让网络拥有更多的可能性。生物角度解释其作用就是细胞核对不同的输入信号其实是做出了非线性的反应的。例如用电流刺激青蛙大腿肌肉，只用电流强度达到时，肌肉才会收缩（这个过程是非线性的）。

池化层：用途是在保证原有特征信息的基础上进行特征的降维，压缩数据和减少参数。在一定程度上可以减少过拟合现象，同时提高模型的容错性。

输出层（全连接层），经过前面的卷积网络层对数据的处理，模型会学到一个高质量的特征图。其实在全连接层之前，如果神经元数目过多，学习能力过强，又可能出现过拟合现象。因此，在全连接层中一般使用Dropout操作来随机删除神经网络中部分神经元之间的链接，以此来降低全连接层的复杂度。当数据来到全连接层时，可以理解为一个简单的多分类网络（如BP神经网络），通过softmax函数得到最终预测输出，整个模型训练完成。

二、LeNet

LeNet-5卷积神经网络的结构组成为也很简单，没啥好说的：两个卷积层convolutions，附带两次下采样（通过池化方法实现），和三个全连接层，如下图所示：

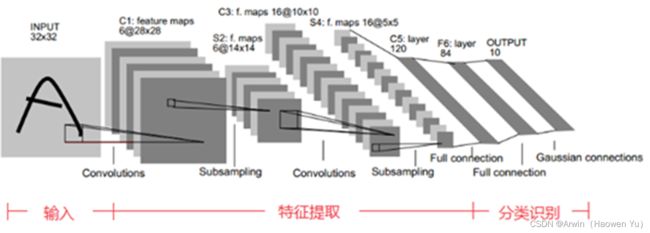
关于LeNet的实现代码使用Tensorflow或者Pytorch可以非常简单的搭建出来，网上也有很多教程，这里就不重复造轮子了。后期关于MobileNet，ShuffleNet等复杂的模型，我会给出完整的代码示例。