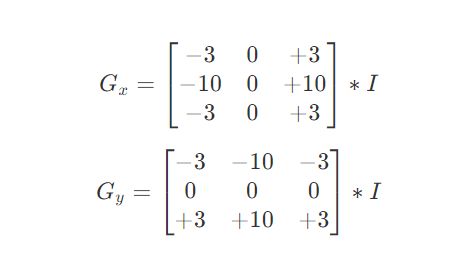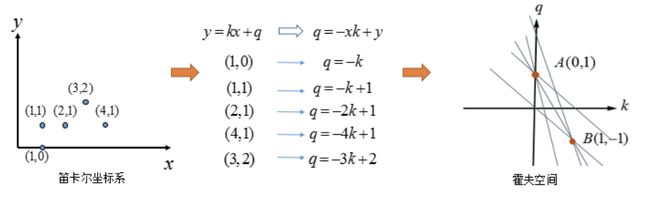OpenCV图像处理（下） 边缘检测+模板匹配+霍夫变换

一、边缘检测

1. 原理

边缘检测是图像处理和计算机视觉中的基本问题，边缘检测的目的是标识数字图像中亮度变化明显的点。图像属性中的显著变化通常反映了属性的重要事件和变化。边缘的表现形式如下图所示：

图像边缘检测大幅度地减少了数据量，并且剔除了可以认为不相关的信息，保留了图像重要的结构属性。有许多方法用于边缘检测，它们的绝大部分可以划分为两类：基于搜索和基于零穿越。

• 基于搜索：通过寻找图像一阶导数中的最大值来检测边界，然后利用计算结果估计边缘的局部方向，通常采用梯度的方向，并利用此方向找到局部梯度模的最大值，代表算法是Sobel算子和Scharr算子。

• 基于零穿越：通过寻找图像二阶导数零穿越来寻找边界，代表算法是Laplacian算子。

2. Sobel检测算子

Sobel边缘检测算法比较简单，实际应用中效率比canny边缘检测效率要高，但是边缘不如Canny检测的准确，但是很多实际应用的场合，sobel边缘却是首选，Sobel算子是高斯平滑与微分操作的结合体，所以其抗噪声能力很强，用途较多。尤其是效率要求较高，而对细纹理不太关心的时候。

2.1 方法

对于不连续的函数，一阶导数可以写作：

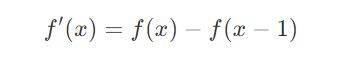
或

所以有：

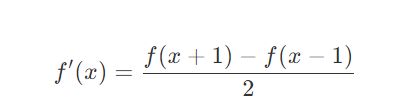
假设要处理的图像为II，在两个方向求导:

• 水平变化: 将图像II 与奇数大小的模版进行卷积，结果为$G_x$​​ 。比如，当模板大小为3时, $G_x$为:
  
• 垂直变化: 将图像II与奇数大小的模板进行卷积，结果为$G_y$​​。比如，当模板大小为3时, $G_y$为
  

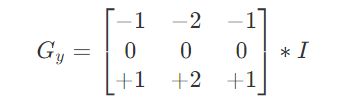
在图像的每一点，结合以上两个结果求出：

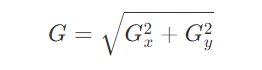
统计极大值所在的位置，就是图像的边缘。

注意：当内核大小为3时, 以上Sobel内核可能产生比较明显的误差， 为解决这一问题，我们使用Scharr函数，但该函数仅作用于大小为3的内核。该函数的运算与Sobel函数一样快，但结果却更加精确，其计算方法为:

2.2 应用

利用OpenCV进行sobel边缘检测的API是：

Sobel_x_or_y = cv2.Sobel(src, ddepth, dx, dy, dst, ksize, scale, delta, borderType)

参数：

• src：传入的图像
• ddepth: 图像的深度
• dx和dy: 指求导的阶数，0表示这个方向上没有求导，取值为0、1。
• ksize: 是Sobel算子的大小，即卷积核的大小，必须为奇数1、3、5、7，默认为3。
  注意：如果ksize=-1，就演变成为3x3的Scharr算子。
• scale：缩放导数的比例常数，默认情况为没有伸缩系数。
• borderType：图像边界的模式，默认值为cv2.BORDER_DEFAULT。

Sobel函数求完导数后会有负值，还有会大于255的值。而原图像是uint8，即8位无符号数，所以Sobel建立的图像位数不够，会有截断。因此要使用16位有符号的数据类型，即cv2.CV_16S。处理完图像后，再使用cv2.convertScaleAbs()函数将其转回原来的uint8格式，否则图像无法显示。

Sobel算子是在两个方向计算的，最后还需要用cv2.addWeighted( )函数将其组合起来

Scale_abs = cv2.convertScaleAbs(x)  # 格式转换函数
result = cv2.addWeighted(src1, alpha, src2, beta) # 图像混合

示例：

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 读取图像
img = cv.imread('./image/horse.jpg',0)
# 2 计算Sobel卷积结果
x = cv.Sobel(img, cv.CV_16S, 1, 0)
y = cv.Sobel(img, cv.CV_16S, 0, 1)
# 3 将数据进行转换
Scale_absX = cv.convertScaleAbs(x)  # convert 转换  scale 缩放
Scale_absY = cv.convertScaleAbs(y)
# 4 结果合成
result = cv.addWeighted(Scale_absX, 0.5, Scale_absY, 0.5, 0)
# 5 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img,cmap=plt.cm.gray),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(result,cmap = plt.cm.gray),plt.title('Sobel滤波后结果')
plt.xticks([]), plt.yticks([])
plt.show()

将上述代码中计算sobel算子的部分中将ksize设为-1，就是利用Scharr进行边缘检测。

x = cv.Sobel(img, cv.CV_16S, 1, 0, ksize = -1)
y = cv.Sobel(img, cv.CV_16S, 0, 1, ksize = -1)

3. Laplacian算子

Laplacian是利用二阶导数来检测边缘 。 因为图像是 “2维”, 我们需要在两个方向求导，如下式所示：

那不连续函数的二阶导数是：

那使用的卷积核是：

API：

laplacian = cv2.Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]])

参数：

• Src: 需要处理的图像，
• Ddepth: 图像的深度，-1表示采用的是原图像相同的深度，目标图像的深度必须大于等于原图像的深度；
• ksize：算子的大小，即卷积核的大小，必须为1,3,5,7。

示例：

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 读取图像
img = cv.imread('./image/horse.jpg',0)
# 2 laplacian转换
result = cv.Laplacian(img,cv.CV_16S)
Scale_abs = cv.convertScaleAbs(result)
# 3 图像展示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img,cmap=plt.cm.gray),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(Scale_abs,cmap = plt.cm.gray),plt.title('Laplacian检测后结果')
plt.xticks([]), plt.yticks([])
plt.show()

4. Canny边缘检测

Canny 边缘检测算法是一种非常流行的边缘检测算法，是 John F. Canny 于 1986年提出的，被认为是最优的边缘检测算法。

4.1 原理

Canny边缘检测算法是由4步构成，分别介绍如下：

• 第一步：噪声去除

由于边缘检测很容易受到噪声的影响，所以首先使用$5\ast 5$高斯滤波器去除噪声，在图像平滑那一章节中已经介绍过。

• 第二步：计算图像梯度

对平滑后的图像使用 Sobel 算子计算水平方向和竖直方向的一阶导数（Gx 和 Gy）。根据得到的这两幅梯度图（Gx 和 Gy）找到边界的梯度和方向，公式如下:

如果某个像素点是边缘，则其梯度方向总是垂直与边缘垂直。梯度方向被归为四类：垂直，水平，和两个对角线方向。

• 第三步：非极大值抑制

在获得梯度的方向和大小之后，对整幅图像进行扫描，去除那些非边界上的点。对每一个像素进行检查，看这个点的梯度是不是周围具有相同梯度方向的点中最大的。如下图所示：

A点位于图像的边缘，在其梯度变化方向，选择像素点B和C，用来检验A点的梯度是否为极大值，若为极大值，则进行保留，否则A点被抑制，最终的结果是具有“细边”的二进制图像。

• 第四步：滞后阈值
  现在要确定真正的边界。 我们设置两个阈值： minVal 和 maxVal。 当图像的灰度梯度高于 maxVal 时被认为是真的边界， 低于 minVal 的边界会被抛弃。如果介于两者之间的话，就要看这个点是否与某个被确定为真正的边界点相连，如果是就认为它也是边界点，如果不是就抛弃。如下图：
  

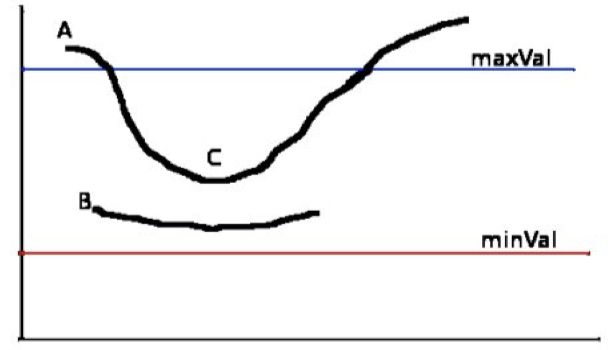
如上图所示，A 高于阈值 maxVal 所以是真正的边界点，C 虽然低于 maxVal 但高于 minVal 并且与 A 相连，所以也被认为是真正的边界点。而 B 就会被抛弃，因为低于 maxVal 而且不与真正的边界点相连。所以选择合适的 maxVal 和 minVal 对于能否得到好的结果非常重要。

4.2 应用

在OpenCV中要实现Canny检测使用的API:

canny = cv2.Canny(image, threshold1, threshold2)

参数：

• image:灰度图，
• threshold1: minval，较小的阈值将间断的边缘连接起来
• threshold2: maxval，较大的阈值检测图像中明显的边缘

示例：

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 图像读取
img = cv.imread('./image/horse.jpg',0)
# 2 Canny边缘检测
lowThreshold = 0
max_lowThreshold = 100
canny = cv.Canny(img, lowThreshold, max_lowThreshold) 
# 3 图像展示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img,cmap=plt.cm.gray),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(canny,cmap = plt.cm.gray),plt.title('Canny检测后结果')
plt.xticks([]), plt.yticks([])
plt.show()

二、模版匹配和霍夫变换

1. 模板匹配

1.1 原理

所谓的模板匹配，就是在给定的图片中查找和模板最相似的区域，该算法的输入包括模板和图片，整个任务的思路就是按照滑窗的思路不断的移动模板图片，计算其与图像中对应区域的匹配度，最终将匹配度最高的区域选择为最终的结果。

实现流程：

• 准备两幅图像：
  1.原图像(I)：在这幅图中，找到与模板相匹配的区域
  2.模板(T)：与原图像进行比对的图像块

• 滑动模板图像和原图像进行比对：
  

将模板块每次移动一个像素 (从左往右，从上往下)，在每一个位置，都计算与模板图像的相似程度。

• 对于每一个位置将计算的相似结果保存在结果矩阵（R）中。如果输入图像的大小（WxH）且模板图像的大小(wxh)，则输出矩阵R的大小为（W-w + 1,H-h + 1）将R显示为图像，如下图所示：
  

• 获得上述图像后，查找最大值所在的位置，那么该位置对应的区域就被认为是最匹配的。对应的区域就是以该点为顶点，长宽和模板图像一样大小的矩阵。

1.2 实现

我们使用OpenCV中的方法实现模板匹配。

API：

res = cv.matchTemplate(img,template,method)

参数：

• img: 要进行模板匹配的图像
• Template ：模板
• method：实现模板匹配的算法，主要有：
  • 平方差匹配(CV_TM_SQDIFF)：利用模板与图像之间的平方差进行匹配，最好的匹配是0，匹配越差，匹配的值越大。
  • 相关匹配(CV_TM_CCORR)：利用模板与图像间的乘法进行匹配，数值越大表示匹配程度较高，越小表示匹配效果差。
  • 利用相关系数匹配(CV_TM_CCOEFF)：利用模板与图像间的相关系数匹配，1表示完美的匹配，-1表示最差的匹配。

完成匹配后，使用cv.minMaxLoc()方法查找最大值所在的位置即可。如果使用平方差作为比较方法，则最小值位置是最佳匹配位置。

示例：

在该案例中，载入要搜索的图像和模板，图像如下所示：

模板如下所示：

通过matchTemplate实现模板匹配，使用minMaxLoc定位最匹配的区域，并用矩形标注最匹配的区域。

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 图像和模板读取
img = cv.imread('./image/wulin2.jpeg')
template = cv.imread('./image/wulin.jpeg')
h,w,l = template.shape
# 2 模板匹配
# 2.1 模板匹配
res = cv.matchTemplate(img, template, cv.TM_CCORR)
# 2.2 返回图像中最匹配的位置，确定左上角的坐标，并将匹配位置绘制在图像上
min_val, max_val, min_loc, max_loc = cv.minMaxLoc(res)
# 使用平方差时最小值为最佳匹配位置
# top_left = min_loc
top_left = max_loc
bottom_right = (top_left[0] + w, top_left[1] + h)
cv.rectangle(img, top_left, bottom_right, (0,255,0), 2)
# 3 图像显示
plt.imshow(img[:,:,::-1])
plt.title('匹配结果'), plt.xticks([]), plt.yticks([])
plt.show()

拓展：模板匹配不适用于尺度变换，视角变换后的图像，这时我们就要使用关键点匹配算法，比较经典的关键点检测算法包括SIFT和SURF等，主要的思路是首先通过关键点检测算法获取模板和测试图片中的关键点；然后使用关键点匹配算法处理即可，这些关键点可以很好的处理尺度变化、视角变换、旋转变化、光照变化等，具有很好的不变性。

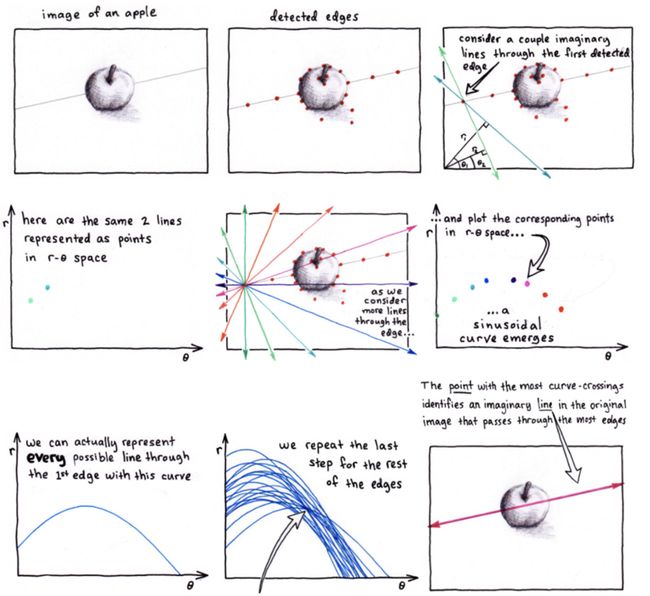
2. 霍夫变换

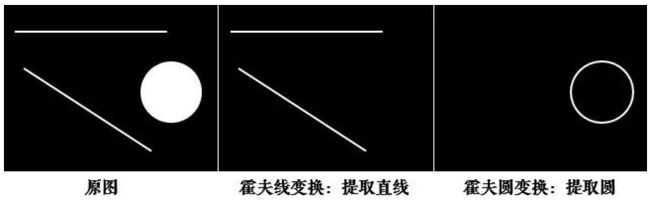
霍夫变换常用来提取图像中的直线和圆等几何形状，如下图所示：

2.1 原理

（1）原理

在笛卡尔坐标系中，一条直线由两个点$A=(x_1,y_1)$和$B=(x_2,y_2)$确定，如下图所示:

将直线y=kx+q可写成关于(k,q)(k,q)的函数表达式：

对应的变换通过图形直观的表示下：

变换后的空间我们叫做霍夫空间。即：笛卡尔坐标系中的一条直线，对应于霍夫空间中的一个点。反过来，同样成立，霍夫空间中的一条线，对应于笛卡尔坐标系中一个点，如下所示：

我们再来看下A、B两个点，对应于霍夫空间的情形：

在看下三点共线的情况：

可以看出如果在笛卡尔坐标系的点共线，那么这些点在霍夫空间中对应的直线交于一点。

如果不止存在一条直线时，如下所示：

我们选择尽可能多的直线汇成的点，上图中三条直线汇成的A、B两点，将其对应回笛卡尔坐标系中的直线：

到这里我们似乎已经完成了霍夫变换的求解。但如果像下图这种情况时：

上图中的直线是$x=2$，那(k,q)怎么确定呢？

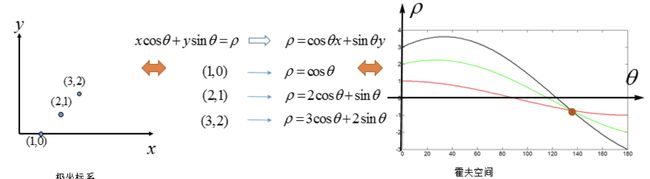
为了解决这个问题，我们考虑将笛卡尔坐标系转换为极坐标。

在极坐标下是一样的，极坐标中的点对应于霍夫空间的线，这时的霍夫空间是不在是参数$(k,q)$的空间，而是$(\rho ,\theta )$的空间，$\rho$是原点到直线的垂直距离，$\theta$表示直线的垂线与横轴顺时针方向的夹角，垂直线的角度为0度，水平线的角度是180度。

我们只要求得霍夫空间中的交点的位置，即可得到原坐标系下的直线。

（2）实现流程

假设有一个大小为100*∗100的图片，使用霍夫变换检测图片中的直线，则步骤如下所示：

• 直线都可以使用$(\rho ,\theta )$ 表示，首先创建一个2D数组，我们叫做累加器，初始化所有值为0，行表示$\rho$ ，列表示$\theta$ 。
  

• 该数组的大小决定了结果的准确性，若希望角度的精度为1度，那就需要180列。对于$\rho$，最大值为图片对角线的距离，如果希望精度达到像素级别，行数应该与图像的对角线的距离相等。

• 取直线上的第一个点$(x,y)$，将其带入直线在极坐标中的公式中，然后遍历$\theta$的取值：0，1，2，…，180，分别求出对应的$\rho$值，如果这个数值在上述累加器中存在相应的位置，则在该位置上加1.

• 取直线上的第二个点，重复上述步骤，更新累加器中的值。对图像中的直线上的每个点都直线以上步骤，每次更新累加器中的值。

• 搜索累加器中的最大值，并找到其对应的$(\rho ,\theta )$，就可将图像中的直线表示出来。

2.2 霍夫线检测

在OpenCV中做霍夫线检测是使用的API是：

cv.HoughLines(img, rho, theta, threshold)

参数：

• img: 检测的图像，要求是二值化的图像，所以在调用霍夫变换之前首先要进行二值化，或者进行Canny边缘检测
• rho、theta: $\rho$ 和$\theta$的精确度
• threshold: 阈值，只有累加器中的值高于该阈值时才被认为是直线。

霍夫线检测的整个流程如下图所示，这是在stackflow上一个关于霍夫线变换的解释：

示例：

检测下述图像中的直线：

import numpy as np
import random
import cv2 as cv
import matplotlib.pyplot as plt
# 1.加载图片，转为二值图
img = cv.imread('./image/rili.jpg')

gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
edges = cv.Canny(gray, 50, 150)

# 2.霍夫直线变换
lines = cv.HoughLines(edges, 0.8, np.pi / 180, 150)
# 3.将检测的线绘制在图像上（注意是极坐标噢）
for line in lines:
    rho, theta = line[0]
    a = np.cos(theta)
    b = np.sin(theta)
    x0 = a * rho
    y0 = b * rho
    x1 = int(x0 + 1000 * (-b))
    y1 = int(y0 + 1000 * (a))
    x2 = int(x0 - 1000 * (-b))
    y2 = int(y0 - 1000 * (a))
    cv.line(img, (x1, y1), (x2, y2), (0, 255, 0))
# 4. 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.imshow(img[:,:,::-1]),plt.title('霍夫变换线检测')
plt.xticks([]), plt.yticks([])
plt.show()

2.3 霍夫圆检测[了解]

（1）原理

圆的表示式是：

其中aa和bb表示圆心坐标，rr表示圆半径，因此标准的霍夫圆检测就是在这三个参数组成的三维空间累加器上进行圆形检测，此时效率就会很低，所以OpenCV中使用霍夫梯度法进行圆形的检测。

霍夫梯度法将霍夫圆检测范围两个阶段，第一阶段检测圆心，第二阶段利用圆心推导出圆半径。

• 圆心检测的原理：圆心是圆周法线的交汇处，设置一个阈值，在某点的相交的直线的条数大于这个阈值就认为该交汇点为圆心。

• 圆半径确定原理：圆心到圆周上的距离（半径）是相同的，确定一个阈值，只要相同距离的数量大于该阈值，就认为该距离是该圆心的半径。

原则上霍夫变换可以检测任何形状，但复杂的形状需要的参数就多，霍夫空间的维数就多，因此在程序实现上所需的内存空间以及运行效率上都不利于把标准霍夫变换应用于实际复杂图形的检测中。霍夫梯度法是霍夫变换的改进，它的目的是减小霍夫空间的维度，提高效率。

（2）API

在OpenCV中检测图像中的圆环使用的是API是：

circles = cv.HoughCircles(image, method, dp, minDist, param1=100, param2=100, minRadius=0,maxRadius=0 )

参数：

• image：输入图像，应输入灰度图像

• method：使用霍夫变换圆检测的算法，它的参数是CV_HOUGH_GRADIENT

• dp：霍夫空间的分辨率，dp=1时表示霍夫空间与输入图像空间的大小一致，dp=2时霍夫空间是输入图像空间的一半，以此类推

• minDist为圆心之间的最小距离，如果检测到的两个圆心之间距离小于该值，则认为它们是同一个圆心

• param1：边缘检测时使用Canny算子的高阈值，低阈值是高阈值的一半。

• param2：检测圆心和确定半径时所共有的阈值

• minRadius和maxRadius为所检测到的圆半径的最小值和最大值

返回：

• circles：输出圆向量，包括三个浮点型的元素——圆心横坐标，圆心纵坐标和圆半径

（3）实现

由于霍夫圆检测对噪声比较敏感，所以首先对图像进行中值滤波。

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
# 1 读取图像，并转换为灰度图
planets = cv.imread("./image/star.jpeg")
gay_img = cv.cvtColor(planets, cv.COLOR_BGRA2GRAY)
# 2 进行中值模糊，去噪点
img = cv.medianBlur(gay_img, 7)  
# 3 霍夫圆检测
circles = cv.HoughCircles(img, cv.HOUGH_GRADIENT, 1, 200, param1=100, param2=30, minRadius=0, maxRadius=100)
# 4 将检测结果绘制在图像上
for i in circles[0, :]:  # 遍历矩阵每一行的数据
    # 绘制圆形
    cv.circle(planets, (i[0], i[1]), i[2], (0, 255, 0), 2)
    # 绘制圆心
    cv.circle(planets, (i[0], i[1]), 2, (0, 0, 255), 3)
# 5 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.imshow(planets[:,:,::-1]),plt.title('霍夫变换圆检测')
plt.xticks([]), plt.yticks([])
plt.show()