【数值分析实验】插值与拟合：拉格朗日插值、牛顿插值、分段插值；线性拟合、最小二乘拟合（python）

调包

import math
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt

插值

拉格朗日插值

#拉格朗日插值
def Lagrange(x,xs,ys):
    n = len(xs)
    ls = [1 for i in range(n)]
    for i in range(n):
        for j in range(n):
            if i != j:
                ls[i] *= (x - xs[j])/(xs[i] - xs[j])
    L = 0
    for i in range(n):
        L += ys[i] * ls[i]
    return L

牛顿插值

通过迭代构建差商表

#牛顿差值
def NewtonIterate(xs,ys,start,end,res):   #res为差商表
    if((end-start)==1):   
        res[end-1][end-start-1]=(ys[end]-ys[start])/(xs[end]-xs[start])
        return res[end-1][end-start-1]
    res[end-1][end-start-1]=(NewtonIterate(xs,ys,start+1,end,res)-NewtonIterate(xs,ys,start,end-1,res))/(xs[end]-xs[start])
    return res[end-1][end-start-1]

def Newton(x,xs,ys):
    n = len(xs)
    res = np.zeros([n - 1, n - 1])
    NewtonIterate(xs, ys, 0, n - 1, res) 
    N = ys[0]
    for i in range(n-1):
        s = 1 
        for j in range(i+1):
            s = s * (x-xs[j]) 
        s *= res[i][i]
        N += s
    return N

分段Hermite插值

# 分段Hermite插值
def Hermite(x,xs,ys,fStr):  
    y_s = [0 for i in range(len(xs))]   
    # 按照xs给ys排序
    data = dict(zip(xs,ys))
    data = sorted(data.items(),key=lambda item:item[0])
    data = dict(data)
    xlist = list(data.keys())
    ylist = list(data.values())
    # 按照xs给y_s排序
    data = dict(zip(xs,y_s))
    data = sorted(data.items(),key=lambda item:item[0])
    data = dict(data)
    y_s = list(data.values())

    n = len(xlist)-1
    if n == 0:
        raise ValueError("n should be greater or equal to 1")
    # 需要把新来的元素判断一下在哪个区间
    i = -1
    for t in xlist:
        if x >= t:
            i += 1
    
    if i == -1 or i > len(xlist)-1:
        raise ValueError("x should be between %f and %f"%(xlist[0],xlist[-1]))  
    if i == len(xlist)-1:
        return ylist[i]
    
    alpha0 = lambda x: ((x-xlist[i+1])/(xlist[i]-xlist[i+1]))**2 * (2*(x-xlist[i])/(xlist[i+1]-xlist[i])+1)
    alpha1 = lambda x: ((x-xlist[i])/(xlist[i+1]-xlist[i]))**2 * (2*(x-xlist[i+1])/(xlist[i]-xlist[i+1])+1)
    beta0 = lambda x: ((x-xlist[i+1])/(xlist[i]-xlist[i+1]))**2 * (x-xlist[i])
    beta1 = lambda x: ((x-xlist[i])/(xlist[i+1]-xlist[i]))**2 * (x-xlist[i+1])
    H = alpha0(x)*ylist[i] + alpha1(x)*ylist[i+1] + beta0(x)*y_s[i] + beta1(x)*y_s[i+1]
    return H

拟合

最小二乘法拟合

xs，ys均为数组，fStrs为函数的str数组

#最小二乘法拟合
def Fit(xs,ys,fStrs):
    m = len(fStrs)
    n = len(xs)
    A = np.ones((m,n))
    #法方程组
    for i in range(1,m):   
        for j in range(n):
            A[i][j] = globals()[fStrs[i]](xs[j])
    A = A.T
    Y = np.array(ys).T
    x = sp.symbols("x")
    c = np.around(np.linalg.solve(np.dot(A.T,A), np.dot(A.T,Y)),6)
    fx = 0
    for i in range(m):
            if i == 0:
                fx += c[i]
            else:
                fx += c[i] * x**i  
    #平方误差
    s2 = 0   
    for i in range(n):
        s = 0
        for j in range(m):
            if j == 0:
                s += c[j]
            else:
                s += c[j] * xs[i]**j
        s2 += (ys[i] - s)**2
    return fx,s2

fx为最终拟合函数，s2为拟合平方误差

例题

#练习3.2.1
xs = [2,3,4,7,8,10,11,14,16,18,19]
ys = [106.42,108.2,109.5,110,109.93,110.49,110.59,110.6,110.76,111,111.2]
f0 = lambda x:1
f1 = lambda x:x
f2 = lambda x:x**2
fStrs = ["f0","f1","f2"]
px,s2 = Fit(xs,ys,fStrs)
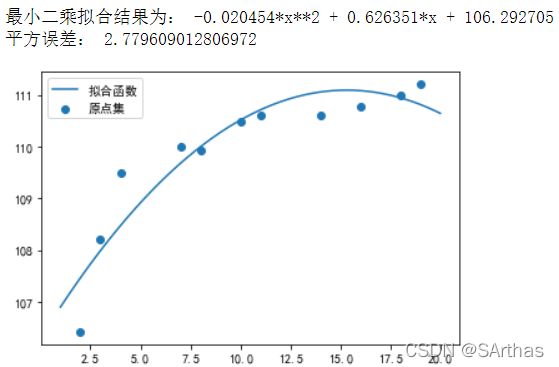
print("最小二乘拟合结果为：",px)
print("平方误差：",s2)
plt.scatter(xs,ys,label = "原点集")
xx = np.arange(1,20,0.01)
yy = []
for xxx in xx:
    yy.append(px.subs("x",xxx))
plt.plot(xx,yy,label = "拟合函数")
plt.legend()
plt.show()

得到结果如下：

最小二乘拟合变式

对形如ae^(bt)的拟合曲线，需对原算法稍作修改

def Fit2(xs,ys):   
    ts = [(1/x) for x in xs]
    zs = [math.log(y) for y in ys]
    n = len(xs)
    A = np.ones((2,n))
    A[1] = [t for t in ts]
    A = A.T
    Y = np.array(zs).T
    c = np.around(np.linalg.solve(np.dot(A.T,A), np.dot(A.T,Y)),6)
    a = np.exp(c[0])
    b = c[1]
    e,x = sp.symbols("e x")
    
    #平方误差
    s2 = 0
    for i in range(n):
        s2 += (ys[i] - (a * np.exp(b / xs[i])))**2
    return a*e**(b/x),s2

例题

xs = [2,3,4,7,8,10,11,14,16,18,19]
ys = [106.42,108.2,109.5,110,109.93,110.49,110.59,110.6,110.76,111,111.2]
px,s2 = Fit2(xs,ys)
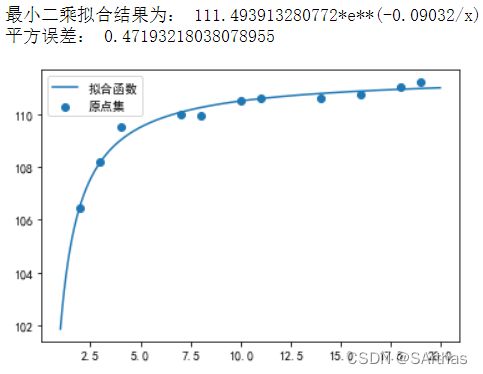
print("最小二乘拟合结果为：",px)
print("平方误差：",s2)
plt.scatter(xs,ys,label = "原点集")
xx = np.arange(1,20,0.01)
yy = []
for xxx in xx:
    yy.append(px.subs([('x',xxx),('e',np.exp(1))]))
plt.plot(xx,yy,label = "拟合函数")
plt.legend()
plt.show()

得到结果如下：