激光雷达构建地图( 覆盖栅格建图)
1.地图分类
环境地图是机器人进行定位(特征地图)和规划(栅格地图)的前提
- 尺度地图
- 拓扑地图
- 语义地图
2.覆盖栅格建图算法
- 把环境分解成一个一个的小栅格
- 每个栅格有两种状态:占用(Occupied)或者空闲(free)
- 非参模型
- 随着地图的增大,内存需求急剧增加
- 天然区分可通行区域,适合进行轨迹规划
1.数学描述
给定机器人的位姿和传感器的观测数据(主要是激光雷达)
d a t a = x 1 , z 1 , x 2 , z 2 , ⋯ , x n , z n (2-1) data = { x_1,z_1,x_2,z_2, \cdots,x_n,z_n }\tag{2-1} data=x1,z1,x2,z2,⋯,xn,zn(2-1)
估计出最可能的地图
m ∗ = a r g m a x m P ( m ∣ d a t a ) ⇒ m ∗ = a r g m a x m P ( m ∣ x 1 : t , z 1 : t ) (2-2) m^*=argmax_mP(m|data)\Rightarrow m^*=argmax_mP(m|x_{1:t},z_{1:t})\tag{2-2} m∗=argmaxmP(m∣data)⇒m∗=argmaxmP(m∣x1:t,z1:t)(2-2)
1.假设
- 栅格地图中的栅格是一个二元随机变量,只能取两个值:占用或者空闲
- p(mi)=1表示被占用,p(mi)=0表示空闲,p(mi)=0.5表示不知道
- 在建图的过程中,环境不会发生改变
- 地图中每一帧栅格都是独立的,因此数学表达式可以表示为
P ( m ) = ∏ p ( m i ) (2-3) P(m)=\prod p(m_i)\tag{2-3} P(m)=∏p(mi)(2-3)
- 地图估计问题表示为:
P ( m ∣ x 1 : t , z 1 : t ) = ∏ p ( m i ∣ x 1 : t , z 1 : t ) (2-4) P(m|x_{1:t},z_{1:t})=\prod p(m_i|x_{1:t},z_{1:t})\tag{2-4} P(m∣x1:t,z1:t)=∏p(mi∣x1:t,z1:t)(2-4)
- 因此,估计环境的地图只需对每个独立的栅格进行估计即可
2.地图估计
mi是一个二元随机变量因此:
P ( m i ∣ x 1 : t , z 1 : t ) = P ( z t ∣ m i , x 1 : t , z 1 : t − 1 ) P ( m i ∣ x 1 : t , z 1 : t − 1 ) P ( z t ∣ x 1 : t , z 1 : t − 1 ) = P ( z t ∣ m i , x t ) P ( m i ∣ x 1 : t − 1 , z 1 : t − 1 ) P ( z t ∣ x 1 : t , z 1 : t − 1 ) (2-5) P(m_i|x_{1:t},z_{1:t})=\frac{P(z_t|m_i,x_{1:t},z_{1:t-1})P(m_i|x_{1:t},z_{1:t-1})}{P(z_t|x_{1:t},z_{1:t-1})}\\ \\ =\frac{P(z_t|m_i,x_{t})P(m_i|x_{1:t-1},z_{1:t-1})}{P(z_t|x_{1:t},z_{1:t-1})}\tag{2-5} P(mi∣x1:t,z1:t)=P(zt∣x1:t,z1:t−1)P(zt∣mi,x1:t,z1:t−1)P(mi∣x1:t,z1:t−1)=P(zt∣x1:t,z1:t−1)P(zt∣mi,xt)P(mi∣x1:t−1,z1:t−1)(2-5)
其中:
P ( z t ∣ m i , x t ) = P ( m i ∣ x t , z t ) P ( z t ∣ x t ) P ( m i ∣ x t ) (2-5) P(z_t|m_i,x_{t})=\frac{P(m_i|x_t,z_t)P(z_t|x_t)}{P(m_i|x_t)}\tag{2-5} P(zt∣mi,xt)=P(mi∣xt)P(mi∣xt,zt)P(zt∣xt)(2-5)
P ( m i ∣ x 1 : t , z 1 : t ) = P ( m i ∣ x t , z t ) P ( z t ∣ x t ) P ( m i ∣ x t ) P ( m i ∣ x 1 : t − 1 , z 1 : t − 1 ) P ( z t ∣ x 1 : t , z 1 : t − 1 ) = P ( m i ∣ x t , z t ) P ( z t ∣ x t ) P ( m i ) P ( m i ∣ x 1 : t − 1 , z 1 : t − 1 ) P ( z t ∣ x 1 : t , z 1 : t − 1 ) (2-7) P(m_i|x_{1:t},z_{1:t})=\frac{P(m_i|x_t,z_t)P(z_t|x_t)}{P(m_i|x_t)}\frac{P(m_i|x_{1:t-1},z_{1:t-1})}{P(z_t|x_{1:t},z_{1:t-1})}\\ \\ =\frac{P(m_i|x_t,z_t)P(z_t|x_t)}{P(m_i)}\frac{P(m_i|x_{1:t-1},z_{1:t-1})}{P(z_t|x_{1:t},z_{1:t-1})}\tag{2-7} P(mi∣x1:t,z1:t)=P(mi∣xt)P(mi∣xt,zt)P(zt∣xt)P(zt∣x1:t,z1:t−1)P(mi∣x1:t−1,z1:t−1)=P(mi)P(mi∣xt,zt)P(zt∣xt)P(zt∣x1:t,z1:t−1)P(mi∣x1:t−1,z1:t−1)(2-7)
mi是个二元随机变量:
P ( ⌝ m i ∣ x 1 : t , z 1 : t ) = = P ( ⌝ m i ∣ x t , z t ) P ( z t ∣ x t ) P ( ⌝ m i ) P ( ⌝ m i ∣ x 1 : t − 1 , z 1 : t − 1 ) P ( z t ∣ x 1 : t , z 1 : t − 1 ) (2-8) P(\urcorner m_i|x_{1:t},z_{1:t})= =\frac{P(\urcorner m_i|x_t,z_t)P(z_t|x_t)}{P(\urcorner m_i)}\frac{P(\urcorner m_i|x_{1:t-1},z_{1:t-1})}{P(z_t|x_{1:t},z_{1:t-1})}\tag{2-8} P(┐mi∣x1:t,z1:t)==P(┐mi)P(┐mi∣xt,zt)P(zt∣xt)P(zt∣x1:t,z1:t−1)P(┐mi∣x1:t−1,z1:t−1)(2-8)
式(2-7)和式(2-8)相比:
P ( m i ∣ x 1 : t , z 1 : t ) P ( ⌝ m i ∣ x 1 : t , z 1 : t ) = P ( m i ∣ x t , z t ) P ( m i ) P ( m i ∣ x 1 : t − 1 , z 1 : t − 1 ) P ( ⌝ m i ) P ( ⌝ m i ∣ x t , z t ) P ( ⌝ m i ∣ x 1 : t − 1 , z 1 : t − 1 ) = P ( m i ∣ x t , z t ) P ( ⌝ m i ∣ x t , z t ) P ( m i ∣ x 1 : t − 1 , z 1 : t − 1 ) P ( ⌝ m i ∣ x 1 : t − 1 , z 1 : t − 1 ) P ( ⌝ m i ) P ( m i ) (2-9) \frac{P(m_i|x_{1:t},z_{1:t})}{P(\urcorner m_i|x_{1:t},z_{1:t})}=\frac{P(m_i|x_t,z_t)}{P(m_i)}\frac{P(m_i|x_{1:t-1},z_{1:t-1})P(\urcorner m_i)}{P(\urcorner m_i|x_t,z_t)P(\urcorner m_i|x_{1:t-1},z_{1:t-1})}\\ \\ =\frac{P(m_i|x_t,z_t)}{P(\urcorner m_i|x_t,z_t)}\frac{P(m_i|x_{1:t-1},z_{1:t-1})}{P(\urcorner m_i|x_{1:t-1},z_{1:t-1})}\frac{P(\urcorner m_i)}{P(m_i)}\tag{2-9} P(┐mi∣x1:t,z1:t)P(mi∣x1:t,z1:t)=P(mi)P(mi∣xt,zt)P(┐mi∣xt,zt)P(┐mi∣x1:t−1,z1:t−1)P(mi∣x1:t−1,z1:t−1)P(┐mi)=P(┐mi∣xt,zt)P(mi∣xt,zt)P(┐mi∣x1:t−1,z1:t−1)P(mi∣x1:t−1,z1:t−1)P(mi)P(┐mi)(2-9)
P ( m i ∣ x 1 : t , z 1 : t ) P ( ⌝ m i ∣ x 1 : t , z 1 : t ) = P ( m i ∣ x t , z t ) 1 − P ( m i ∣ x t , z t ) P ( m i ∣ x 1 : t − 1 , z 1 : t − 1 ) 1 − P ( m i ∣ x 1 : t − 1 , z 1 : t − 1 ) 1 − P ( m i ) P ( m i ) (2-10) \frac{P(m_i|x_{1:t},z_{1:t})}{P(\urcorner m_i|x_{1:t},z_{1:t})}=\frac{P(m_i|x_t,z_t)}{1-P( m_i|x_t,z_t)}\frac{P(m_i|x_{1:t-1},z_{1:t-1})}{1-P( m_i|x_{1:t-1},z_{1:t-1})}\frac{1-P( m_i)}{P(m_i)}\tag{2-10} P(┐mi∣x1:t,z1:t)P(mi∣x1:t,z1:t)=1−P(mi∣xt,zt)P(mi∣xt,zt)1−P(mi∣x1:t−1,z1:t−1)P(mi∣x1:t−1,z1:t−1)P(mi)1−P(mi)(2-10)
对于P(X),定义对应的Log-Odd项:
l ( x ) = p ( x ) 1 − p ( x ) (2-11) l(x)=\frac{p(x)}{1-p(x)}\tag{2-11} l(x)=1−p(x)p(x)(2-11)
则:
P ( x ) = 1 − 1 1 + e x p ( l ( x ) ) (2-12) P(x)=1-\frac{1}{1+exp(l(x)) }\tag{2-12} P(x)=1−1+exp(l(x))1(2-12)
则式(2-10)则变成:
l ( m i ∣ x 1 : t , z 1 : t ) = l ( m i ∣ x t , z t ) + l ( m i ∣ x 1 : t − 1 , z 1 : t − 1 ) − l ( m i ) (2-13) l(m_i|x_{1:t},z_{1:t})=l(m_i|x_t,z_t)+l(m_i|x_{1:t-1},z_{1:t-1})-l( m_i)\tag{2-13} l(mi∣x1:t,z1:t)=l(mi∣xt,zt)+l(mi∣x1:t−1,z1:t−1)−l(mi)(2-13)
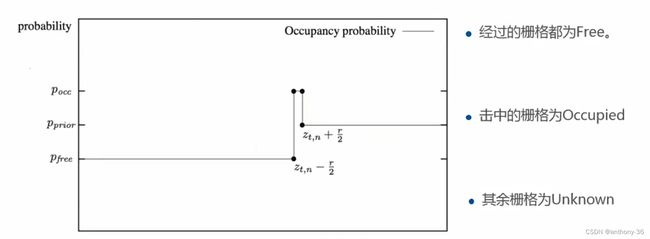
- l ( m i ∣ x t , z t ) l(m_i|x_t,z_t) l(mi∣xt,zt)表示激光雷达的逆观测模型
- l ( m i ∣ x 1 : t − 1 , z 1 : t − 1 ) l(m_i|x_{1:t-1},z_{1:t-1}) l(mi∣x1:t−1,z1:t−1)表示栅格mi在t-1时刻的状态
- l ( m i ) l( m_i) l(mi)表示栅格mi的先验值,该值对所有栅格都相同
3.算法流程
- 算法对某个栅格进行操作的时候,只有加法操作,因此具有非常高的更新速度。
- 更新时需要知道传感器逆测量模型。