SKlearn学习笔记1 回归分析

@TOC

序号	回归算法名称	方法及参数
1	线性回归	sklearn.linear_model.LinearRegression
2	多项式回归	sklearn.preprocessing.PolynomialFeatures
3.1	LASSO回归	sklearn.linear_model.Lasso
3.2	岭回归	sklearn.linear_model.Ridge
3.3	弹性网络	sklearn.linear_model.ElasticNet
4	SVM支持向量机	sklearn.svm.SVR
5	KNN近邻	sklearn.neighbors.KNeighborsRegressor
6	高斯过程	sklearn.gaussian_process.GaussianProcessRegressor
7	贝叶斯岭回归	sklearn.linear_model.BayesianRidge
9	随机森林	sklearn.ensemble.RandomForestRegressor
10	XGBoost	xgboost.XGBRegressor
11	Adaboost	sklearn.ensemble.AdaBoostRegressor
12	梯度提升GBRT	sklearn.ensemble.GradientBoostingRegressor
13	逻辑回归	sklearn.linear_model.LogisticRegression
14	最小角回归	sklearn.linear_model.Lars

1 线性回归

线性回归(Linear Regression)是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法
线性回归利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模。 这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。

• 一元线性回归：$y=a+bx$
• 多元线性回归：$y=a_0+a_1{x}_1+a_2{x}_2+\cdots +a_n{x}_n$

"线性回归求解波士顿房价问题"

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score

# 导入数据
dataset = load_boston()
print(dataset.feature_names)

df = pd.DataFrame(data=dataset.data, columns=dataset.feature_names)
df['price']=dataset.target
print(df.describe())
print(df.shape)

# 相关性分析
print(df.corr())

# 分割训练集与测试集
x = df.iloc[:,0:13]
y = df.iloc[:,-1]
print(x.shape, y.shape)

x_train, x_test, y_train, y_test = train_test_split(x,y, test_size=0.4)


# 建立模型，训练后预测
model = LinearRegression()
model.fit(x_train, y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.7339502509738509

2 多项式回归

多项式回归模型：$y=a_0+a_1{x}_1+a_2{x}_2+\cdots +a_n{x}_n+a_{12}{x}_1{x}_2+\cdots +a_{n-1,n}{x}_{n-1}{x}_n+\cdots +a_{nn}{x}_n^2$

# 建立多项式回归模型，训练后求解
poly_reg = PolynomialFeatures(degree=2)
x_poly = poly_reg.fit_transform(x_train)
model = LinearRegression()
model.fit(x_poly, y_train)
y_test_pred = model.predict(poly_reg.transform(x_test))
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.7162473166128823

3 Lasso回归、Ridge回归和Elastic Net

1.过拟合
当样本特征很多，样本数相对较少时，模型容易陷入过拟合。为了缓解过拟合问题，有两种方法：

   方法一：减少特征数量（人工选择重要特征来保留，会丢弃部分信息）。

   方法二：正则化（减少特征参数w ^的数量级）。

2.正则化（Regularization）
正则化是结构风险（损失函数+正则化项）最小化策略的体现，是在经验风险（平均损失函数）上加一个正则化项。正则化的作用就是选择经验风险和模型复杂度同时较小的模型。

防止过拟合的原理：正则化项一般是模型复杂度的单调递增函数，而经验风险负责最小化误差，使模型偏差尽可能小经验风险越小，模型越复杂，正则化项的值越大。要使正则化项也很小，那么模型复杂程度受到限制，因此就能有效地防止过拟合。

3.线性回归正则化
正则化一般具有如下形式的优化目标：

其中，$\lambda \ge 0$是用来平衡正则化项和经验风险的系数。
正则化项可以是模型参数向量的范数，经常用的有$L_1$范数，$L_2$范数($L_1$范数：$||x|{|}_1=\sum _{i=1}^m|x_i|$, $L_2范数：||x|{|}_2=\sqrt{\sum _{i=1}^m{x}_i^2}$)。

我们考虑最简单的线性回归模型。

给定数据集$D=\{(x_i,y_i){\}}_{i=1}^m$，其中，$x_i=(x_{i1},x_{i2},\cdots ,x_{id}),y_i\in R$

（1）LASSO回归
$L_1$范数正则化（LASSO，Least Absoulute Shrinkage and Selection Operator，最小绝对收缩选择算子）
代价函数为：

（2）岭回归
$L_2$范数正则化（Ridge Regression，岭回归）
代价函数为：

（3）Elastic Net
L_1正则项L_2正则项结合（Elastic Net）

代价函数为：

其中，$L_1$范数正则化、$L_2$范数正则化都有助于降低过拟合风险，$L_2$范数通过对参数向量各元素平方和求平方根，使得$L_2$范数最小，从而使得参数$w $的各个元素接近0，但不等于0。而$L_1$范数正则化比$L_2$范数更易获得“稀疏”解，即$L_1$范数正则化求得的$w$会有更少的非零分量，所以$L_1$范数可用于特征选择，而$L_2$范数在参数规则化时经常用到（事实上，$L_0$范数得到的“稀疏”解最多，但$L_0$范数是x中非零元素的个数，不连续，难以优化求解。因此常用$L_1$范数来近似代替）。
https://blog.csdn.net/pxhdky/article/details/82960659

4 SVM支持向量机

支持向量机的优势在于:

• 在高维空间中非常高效.
• 即使在数据维度比样本数量大的情况下仍然有效.
• 在决策函数（称为支持向量）中使用训练集的子集,因此它也是高效利用内存的.
• 通用性: 不同的核函数 核函数 与特定的决策函数一一对应.

支持向量机的缺点包括:

• 如果特征数量比样本数量大得多,在选择核函数 核函数 时要避免过拟合,而且正则化项是非常重要的.
• 支持向量机不直接提供概率估计,这些都是使用昂贵的五次交叉验算计算的.

支持向量分类的方法可以被扩展用作解决回归问题. 这个方法被称作支持向量回归.

支持向量分类生成的模型(如前描述)只依赖于训练集的子集,因为构建模型的 cost function 不在乎边缘之外的训练点. 类似的,支持向量回归生成的模型只依赖于训练集的子集, 因为构建模型的 cost function 忽略任何接近于模型预测的训练数据.

支持向量分类有三种不同的实现形式: SVR, NuSVR 和 LinearSVR. 在只考虑线性核的情况下, LinearSVR 比 SVR 提供一个更快的实现形式, 然而比起 SVR 和 LinearSVR, NuSVR 实现一个稍微不同的构思(formulation).

对于SVM算法，我们首先导入sklearn.svm中的SVR模块。SVR()就是SVM算法来做回归用的方法（即输入标签是连续值的时候要用的方法），通过以下语句来确定SVR的模式（选取比较重要的几个参数进行测试。随机选取一只股票开始相关参数选择的测试）。
svr = SVR(kernel=’rbf’, C=1e3, gamma=0.01)

class sklearn.svm.SVR(*, kernel=‘rbf’, degree=3, gamma=‘scale’, coef0=0.0, tol=0.001, C=1.0, epsilon=0.1, shrinking=True, cache_size=200, verbose=False, max_iter=-1)

• kernel:核函数的类型，一般常用的有{‘linear’，‘poly’，‘rbf’，‘sigmoid’，‘precomputed’}，默认=‘rbf’
• C:惩罚因子
  C表征你有多么重视离群点，C越大越重视，越不想丢掉它们。C值大时对误差分类的惩罚增大，C值小时对误差分类的惩罚减小。当C越大，趋近无穷的时候，表示不允许分类误差的存在，margin越小，容易过拟合；当C趋于0时，表示我们不再关注分类是否正确，只要求margin越大，容易欠拟合。如图所示发现当使用1e3时最为适宜。
• gamma:
  是’rbf’，’poly’和’sigmoid’的核系数且gamma的值必须大于0。随着gamma的增大，存在对于测试集分类效果差而对训练分类效果好的情况，并且容易泛化误差出现过拟合。如图发现gamma=0.01时准确度最高。
• degree
  多项式核函数的度（“ poly”）。被所有其他内核忽略。

方法

• fit(X, y[, sample_weight])
• get_params([deep])
• predict(X)
• score(X, y[, sample_weight])
• set_params(**params)

# 支持向量机SVM回归
from sklearn.svm import SVR
model = SVR(kernel='linear', gamma=0.01, C=1, epsilon=0.2)
model.fit(x_train,y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.7407645230361497

在NuSVR中，参数nu代表训练集训练的错误率的上限，或者说支持向量的百分比下限，取值范围为(0,1],默认是0.5.它和惩罚系数C类似，都可以控制惩罚的力度。

# 支持向量机SVM回归
from sklearn.svm import NuSVR
model = NuSVR(kernel='linear',nu=0.5, gamma=0.1, C=1) # 用参数Nu控制支持向量数量
model.fit(x_train,y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.6936282895492922

5 KNN最近邻

KNeighborsRegressor、RadiusNeighborsRegressor
KNN基本算法思路：一个样本在特征空间中k个最相似（最邻近）的样本大多数属于同一个类别。（物以类聚）

距离选取：euclidean,manhattan,minkonwski

K值可以基于方根误差（RMSE）确定，启发式的找到一个最优近邻数K。

R中的实用包（FNN）

实现案例

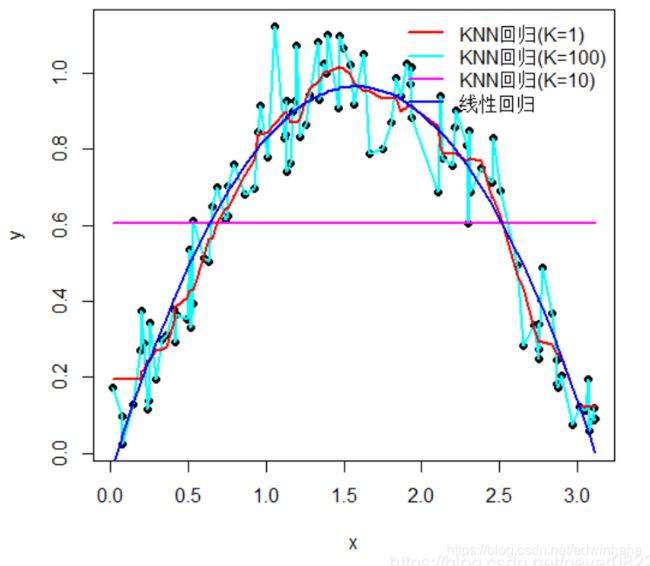
KNN回归在R中可以使用FNN::knn.reg实现，下面通过一个简单的例子说明，图中的黑色实心点表示样本观测值，红、天蓝、紫和蓝色曲线分别表示KNN(k=1,k=100,k=10)以及线性回归，经计算K=10时的RMSE为0.1035,而线性回归的RMSE为0.1055，因此KNN回归略优于线性回归，且从图中可以看出，KNN的拟合曲线更加灵活，能够包含更多的样本信息。

class sklearn.neighbors.KNeighborsRegressor(n_neighbors=5, *, weights=‘uniform’, algorithm=‘auto’, leaf_size=30, p=2, metric=‘minkowski’, metric_params=None, n_jobs=None, **kwargs)
参数：

• n_neighbors：默认情况下用于kneighbors查询的邻居数，默认为5
• weights：权重函数，‘uniform’, ‘distance’，默认‘uniform’
• algorithm：{‘auto’，‘ball_tree’，‘kd_tree’，‘brute’}，用于计算最近邻居的可选算法
• leaf_size：传递给BallTree或KDTree的叶子大小，默认30
• p：Minkowski度量的幂参数，默认为2。当p = 1时，这等效于对p = 2使用manhattan_distance（l1）和euclidean_distance（l2）。对于任意p，使用minkowski_distance（l_p）。
• metric：用于树的距离度量。默认度量标准为minkowski，p = 2等于标准欧几里德度量标准。
  使用自动搜索调参的方法，可以调试的参数有：
• n_neighbors ：一般也不需要更改，默认5是最佳的。也可以尝试在小范围调试看看效果。
• leaf_size：一般默认是30。可以在其值不大的范围内调试看看效果。
• weights ：参数有‘uniform’和‘distance’，可以选择调试。
  方法：
• fit(X, y)
• get_params([deep])
• kneighbors([X, n_neighbors, return_distance])
• kneighbors_graph([X, n_neighbors, mode])
• predict(X)
• score(X, y[, sample_weight])
• set_params(**params)

# 使用KNN回归算法求解波士顿房价问题
from sklearn.neighbors import KNeighborsRegressor
model = KNeighborsRegressor(n_neighbors=4)
model.fit(x_train,y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.47571332192994253

6 高斯过程

https://blog.csdn.net/qq_20195745/article/details/82721666
高斯过程 (GP) 是一种常用的监督学习方法，旨在解决回归问题和概率分类问题。
GaussianProcessRegressor 类实现了回归情况下的高斯过程(GP)模型。
class sklearn.gaussian_process.GaussianProcessRegressor(kernel=None, *, alpha=1e-10, optimizer=‘fmin_l_bfgs_b’, n_restarts_optimizer=0, normalize_y=False, copy_X_train=True, random_state=None)
方法：

• fit(X, y) get_params([deep])
• log_marginal_likelihood([theta, …])
• predict(X[, return_std, return_cov])
• sample_y(X[, n_samples, random_state])
• score(X, y[, sample_weight])
• set_params(**params)

# 高斯过程回归求解波士顿房价问题
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import DotProduct, WhiteKernel
kernel = DotProduct() + WhiteKernel()
model = GaussianProcessRegressor(kernel=kernel, random_state=0)
model.fit(x_train, y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.7606442392766215

7 贝叶斯岭回归

# 贝叶斯回归求解波士顿房价问题
from sklearn.linear_model import BayesianRidge
model = BayesianRidge()
model.fit(x_train,y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.7401039776625611

8 决策树

# 决策树回归求解波士顿房价问题
from sklearn.tree import DecisionTreeRegressor
model = DecisionTreeRegressor(max_depth=5)
model.fit(x_train,y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.7877710469413343

9 随机森林

# 使用随机森林回归器求解波士顿房价问题
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor(n_estimators=100,random_state=0)
model.fit(x_train,y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.817486177599523

10 XGBoost

# XGBoost回归求解波士顿房价问题
from xgboost import XGBRegressor
model = XGBRegressor(max_depth=5, learning_rate=0.1, n_estimators=160, objective='reg:gamma')
model.fit(x_train,y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.865145581323534

# XGBoost回归求解波士顿房价问题
from xgboost import XGBRFRegressor
model = XGBRFRegressor(max_depth=3, learning_rate=0.01, n_estimators=5, objective='reg:gamma')
model.fit(x_train,y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= -5.535280877062936

11 Adaboost

# Adaboost回归求解波士顿房价问题
from sklearn.ensemble import AdaBoostRegressor
model = AdaBoostRegressor(n_estimators=50)
model.fit(x_train,y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.8113261799109158

12 梯度提升GBRT

# GBRT回归求解波士顿房价问题
from sklearn.ensemble import GradientBoostingRegressor
model = GradientBoostingRegressor(n_estimators=50)
model.fit(x_train,y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.8759402217883654

13 Bagging

# Bagging回归求解波士顿房价问题
from sklearn.ensemble import BaggingRegressor
model = BaggingRegressor(n_estimators=100, oob_score=True, random_state=1010)
model.fit(x_train,y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.7596921863730038

14 极端随机树

# 极端随机树回归求解波士顿房价问题
from sklearn.ensemble import ExtraTreesRegressor
model = ExtraTreesRegressor(n_estimators=100,max_depth=5)
model.fit(x_train,y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.8363817980785304

15 逻辑回归

数据要添加.astype(‘int’)，否则报错

# 分割训练集与测试集
x = df.iloc[:,0:13].astype('int')
y = df.iloc[:,-1].astype('int')

from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(x_train,y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.3669574324095297

16 最小角回归

# 最小角回归求解波士顿房价问题
from sklearn.linear_model import Lars
model = Lars()
model.fit(x_train,y_train)
y_test_pred = model.predict(x_test)
test_score = r2_score(y_test, y_test_pred)
print("R^2得分=",test_score)

运行结果：

R^2得分= 0.6765595314076014

参考资料

https://www.cntofu.com/book/170/index.html