蚁群算法小结及算法实例（附Matlab代码）

目录

1、基本蚁群算法

2、基本蚁群算法的流程

3、关键参数说明

3.1 信息素启发式因子 α

3.2 期望启发因子 β

3.3 信息素蒸发系数 ρ

3.4 蚂蚁数目 m

3.5 信息素强度 Q 对算法性能的影响

3.6 最大进化代数 G

4、MATLAB仿真实例

4.1 蚁群算法求解旅行商问题（TSP）

蚁群算法求解旅行商问题MATLAB源程序：

4.2 蚁群算法求解二元函数极值

蚁群算法求解二元函数极值MATLAB源程序：

5、蚁群算法的特点

6、改进的蚁群算法

6.1 精英蚂蚁系统

6.2 最大最小蚂蚁系统

6.3 基于排序的蚁群算法

6.4 自适应蚁群算法

---

1、基本蚁群算法

基本蚁群算法可以表述如下：在算法的初始时刻，将 \(m\) 只蚂蚁随机地放到 \(n\) 座城市，同时，将每只蚂蚁的禁忌表 \(tabu\) 的第一个元素设置为它当前所在的城市。此时各路径上的信息素量相等，设 \(\tau_{ij}(0) = c\)（\(c\) 为一较小的常数），接下来，每只蚂蚁根据路径上残留的信息素量和启发式信息（两城市间的距离）独立地选择下一座城市，在时刻 \(t\)，蚂蚁 \(k\) 从城市 \(i\) 转移到城市 \(j\) 的概率 \(p_{ij}^k(t)\)为：

$$p_{ij}^k(t) = \begin{cases} \frac{[\tau_{ij}(t)]^{\alpha} \cdot [\eta_{ij}(t)]^{\beta}}{\sum_{s \in J_k(i)} {[\tau_{is}(t)]^{\alpha} \cdot [\eta_{is}(t)]^{\beta}}}, & \text{当 \(j \in J_k(i)\) 时} \\ 0, & \text{其它} \\ \end{cases}    \quad \text {(1)} $$

其中，\(J_k(i) = \lbrace 1，2，…，n \rbrace -tabu_k\) 表示蚂蚁 k 下一步允许选择的城市集合。禁忌 表 \(tabu_k\) 记录了蚂蚁 k 当前走过的城市。当所有 n 座城市都加入到禁忌表 \(tabu_k\) 中时，蚂蚁 k 便完成了一次周游，此时蚂蚁 k 所走过的路径便是 TSP 问题的一个可行解。式（1）中的 \(\eta_{ij}\) 是一个启发式因子，表示蚂蚁从城市 i 转移到城市 j 的期望程度。在蚁群算法中，\(\eta_{ij}\) 通常取城市 i 与城市 j 之间距离的倒数。\alpha 和 \beta 分别表示信息素和期望启发式因子的相对重要程度。当所有蚂蚁完成一次周游 后，各路径上的信息素根据式（2）更新：

$$ \tau_{ij}(t+n)=(1- \rho) \cdot \tau_{ij}(t)+ \Delta \tau_{ij}  \quad \text {(2)} $$ 

$$ \Delta \tau_{ij}= \sum_{k=1}^{m} \Delta \tau_{ij}^k  \quad \text {(3)} $$

其中：\(\rho（0< \rho <1）\)表示路径上信息素的蒸发系数，\(1- \rho\) 表示信息素的持久性系数；\(\Delta \tau_{ij}\)  表示本次迭代中边 \(ij\) 上信息素的增量，\(\Delta \tau_{ij}^k\) 表示第 k 只蚂蚁在本次迭代中留在边 \(ij\) 上的信息素量。如果蚂蚁 k 没有经过边 \(ij\)，则 \(\Delta \tau_{ij}^k\) 的值为零。\(\Delta \tau_{ij}^k\) 表示为：

$$\Delta \tau_{ij}^k = \begin{cases} Q/L_K, & \text{当蚂蚁 k 在本次周游中经过边 \(ij\) 时} \\ 0, & \text{其它} \\ \end{cases}    \quad \text {(4)} $$

其中，Q 为正常数，\(L_K\)表示第 k 只蚂蚁在本次周游中所走过路径的长度。

M. Dorigo 提出了 3 种蚁群算法的模型，式（4）称为 ant-cycle，另外两个模型分别称为 ant-quantity 和 ant-density，其差别主要在（4）式，即在 ant-quantity 模型中为：

$$\Delta \tau_{ij}^k = \begin{cases} Q/d_{ij}, & \text{当蚂蚁 k 在时刻 t 和 t+1 经过边 \(ij\) 时} \\ 0, & \text{其它} \\ \end{cases}    \quad \text {(5)} $$

在 ant-density 模型中为：

$$\Delta \tau_{ij}^k = \begin{cases} Q, & \text{当蚂蚁 k 在时刻 t 和 t+1 经过边 \(ij\) 时} \\ 0, & \text{其它} \\ \end{cases}    \quad \text {(6)} $$

蚁群算法实际上是正反馈原理和启发式算法相结合的一种算法。在选择路径时，蚂蚁不仅利用了路径上的信息素，而且用到了城市间距离的倒数作为启发式因子。实验结果表明，ant-cycle 模型比 ant-quantity 和 ant-density 模型有更好的性能。这是因为 ant-cycle 模型利用全局信息更新路径上的信息素量，而 ant-quantity 和 ant-density 模型使用局部信息。

2、基本蚁群算法的流程

基本蚁群算法的具体实现步骤如下：

（1）参数初始化。令时间 \(t = 0\) 和循环次数 \(N_c = 0\)，设置最大循环次数 G，将 m 个蚂蚁置于 n 个元素（城市）上，令有向图上每条边 (i，j) 的初始化信息量 \(\tau_{ij}(t) = c\)，其中 \(c\) 表示常数，且初始时刻 \(\Delta \tau_{ij}(0) = 0\)。

（2）循环次数 \(N_c = N_c + 1\)。

（3）蚂蚁的禁忌表索引号 k = 1。

（4）蚂蚁数目 k = k + 1。

（5）蚂蚁个体根据状态转移概率公式（1）计算的概率选择元素 j 并前进，\(j \in J_k(i)\)。

（6）修改禁忌表指针，即选择好之后将蚂蚁移动到新的元素，并把该元素移动到该蚂蚁个体的禁忌表中。

（7）若集合 C 中元素未遍历完，即 k < m，则跳转到第（4）步；否则执行第（8）步。

（8）记录本次最佳路线。

（9）根据式（2）和式（3）更新每条路径上的信息量。

（10）若满足结束条件，即如果循环次数 \(N_c \geq G\) ，则循环结束并输出程序优化结果；否则清空禁忌表并跳转到第（2）步。

蚁群算法的运算流程如下图所示：

3、关键参数说明

在蚁群算法中，不仅信息素和启发函数乘积以及蚂蚁之间的合作行为会严重影响到算法的收敛性，蚁群算法的参数也是影响其求解性能和效率的关键因素。信息素启发式因子 α、期望启发因子 β、信息素蒸发系数 ρ、信息素强度 Q、蚂蚁数目 m 等都是非常重要的参数，其选取方法和选取原则直接影响到蚁群算法的全局收敛性和求解效率。

3.1 信息素启发式因子 α

信息素启发式因子 α 代表信息量对是否选择当前路径的影响程度，即反映蚂蚁在运动过程中所积累的信息量在指导蚁群搜索中的相对重要程度。α 的大小反映了蚁群在路径搜索中随机性因素作用的强度，其值越大，蚂蚁在选择以前走过的路径的可能性就越大，搜索的随机性就会减弱；而当启发式因子 α 的值过小时，则易使蚁群的搜索过早陷于局部最优。根据经验，信息素启发式因子 α 取值范围一般为 [1，4] 时，蚁群算法的综合求解性能较好。

3.2 期望启发因子 β

期望启发因子 β 表示在搜索时路径上的信息素在指导蚂蚁选择路径时的向导性，它的大小反映了蚁群在搜索最优路径的过程中的先验性和确定性因素的作用强度。期望启发因子 β 的值越大，蚂蚁在某个局部点上选择局部最短路径的可能性就越大，虽然这个时候算法的收敛速度得以加快，但蚁群搜索最优路径的随机性减弱，而此时搜索易于陷入局部最优解。根据经验，期望启发因子 β 取值范围一般为 [3，5] 时，蚁群算法的综合求解性能较好。

实际上，信息素启发式因子 α 和期望启发因子 β 是一对关联性很强的参数：蚁群算法的全局寻优性能，首先要求蚁群的搜索过程必须要有很强的随机性；而蚁群算法的快速收敛性能，又要求蚁群的搜索过程必须要有较高的确定性。因此，两者对蚁群算法性能的影响和作用是相互配合、密切相关的，算法要获得最优解，就必须在这二者之间选取一个平衡点，只有正确选定它们之间的搭配关系，才能避免在搜索过程中出现过早停滞或陷入局部最优等情况的发生。

3.3 信息素蒸发系数 ρ

蚁群算法中的人工蚂蚁是具有记忆功能的，随着时间的推移，以前留下的信息素将会逐渐消逝，蚁群算法与其他各种仿生进化算法一样，也存在着收敛速度 慢、容易陷入局部最优解等缺陷，而信息素蒸发系数 ρ 大小的选择将直接影响到整个蚁群算法的收敛速度和全局搜索性能。在蚁群算法的抽象模型中，ρ 表示信息素蒸发系数，1 - ρ 则表示信息素持久性系数。因此，ρ 的取值范围应该是 0～1 之间的一个数，表示信息素的蒸发程度，它实际上反映了蚂蚁群体中个体之间相互影响的强弱。ρ 过小时，则表示以前搜索过的路径被再次选择的可能性过大，会影响到算法的随机性能和全局搜索能力；ρ 过大时，说明路径上的信息素挥发的相对变多，虽然可以提高算法的随机搜索性能和全局搜索能力，但过多无用搜索操作势必会降低算法的收敛速度。

3.4 蚂蚁数目 m

蚁群算法是一种随机搜索算法，与其他模拟进化算法一样，通过多个候选解组成的群体进化过程来寻求最优解，在该过程中不仅需要每个个体的自适应能力，更需要群体之间的相互协作能力。蚁群在搜索过程中之所以表现出复杂有序的行为，是因为个体之间的信息交流与相互协作起着至关重要的作用。

对于旅行商问题，单个蚂蚁在一次循环中所经过的路径，表现为问题可行解集中的一个解，m 只蚂蚁在一次循环中所经过的路径，则表现为问题解集中的一个子集。显然，子集增大（即蚂蚁数量增多），可以提高蚁群算法的全局搜索能力以及算法的稳定性；但蚂蚁数目增大后，会使大量的曾被搜索过的解（路径）上的信息素的变化趋于平均，信息正反馈的作用不明显，虽然搜索的随机性得到了加强，但收敛速度减慢；反之，子集较小（蚂蚁数量少），特别是当要处理的问题规模比较大时，会使那些从来未被搜索到的解（路径）上的信息素减小到接近于 0，搜索的随机性减弱，虽然收敛速度加快了，但会使算法的全局性能降低，算法的稳定性差，容易出现过早停滞现象。m 一般取 10～50。

3.5 信息素强度 Q 对算法性能的影响

在蚁群算法中，各个参数的作用实际上是紧密联系的，其中对算法性能起着主要作用的是信息启发式因子 α、期望启发式因子 β 和信息素挥发因子 ρ 这三个参数，总信息量 Q 对算法性能的影响有赖于上述三个参数的选取，以及算法模型的选取。例如，在 ant-cycle 模型和 ant-quantity 模型中，总信息量 Q 所起的作用显然是有很大差异的，即随着问题规模的不同，其影响程度也将不同。相关人员研究结果表明：总信息量 Q 对 ant-cycle 模型蚁群算法的性能没有明显的影响。因此，在算法参数的选择上，参数 Q 不必作特别的考虑，可以任意选取。

3.6 最大进化代数 G

最大进化代数 G 是表示蚁群算法运行结束条件的一个参数，表示蚁群算法运行到指定的进化代数之后就停止运行，并将当前群体中的最佳个体作为所求问题的最优解输出。一般 G 取 100～500。

4、MATLAB仿真实例

4.1 蚁群算法求解旅行商问题（TSP）

例 1  旅行商问题（TSP 问题）。假设有一个旅行商人要拜访全国 31 个省会城市，他需要选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择要求是：所选路径的路程为所有路径之中的最小值。

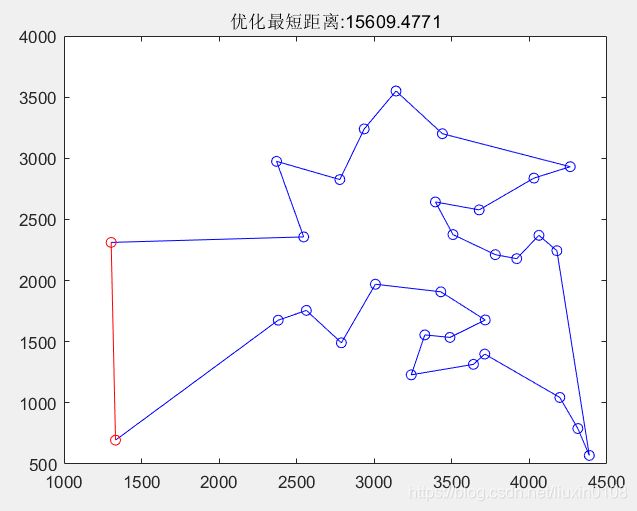
全国 31 个省会城市的坐标为 [1304 2312; 3639 1315; 4177 2244; 3712 1399; 3488 1535; 3326 1556; 3238 1229; 4196 1004; 4312 790; 4386 570; 3007 1970; 2562 1756; 2788 1491; 2381 1676; 1332 695; 3715 1678; 3918 2179; 4061 2370; 3780 2212; 3676 2578; 4029 2838; 4263 2931; 3429 1908; 3507 2367; 3394 2643; 3439 3201; 2935 3240; 3140 3550; 2545 2357; 2778 2826; 2370 2975]。

解：仿真过程如下：

（1）初始化蚂蚁个数 m = 50，信息素重要程度参数 Alpha = 1，启发式因子重要程度参数 Beta = 5，信息素蒸发系数 Rho = 0.1，最大迭代次数 G = 200，信息素增加强度系数 Q = 100。

（2）将 m 个蚂蚁置于 n 个城市上，计算待选城市的概率分布，m 只蚂蚁按概率函数选择下一座城市，完成各自的周游。

（3）记录本次迭代最佳路线，更新信息素，禁忌表清零。

（4）判断是否满足终止条件：若满足，则结束搜索过程，输出优化值；若不满足，则继续进行迭代优化。

 

优化后的路径和适应度进化曲线如下图所示：

蚁群算法求解旅行商问题MATLAB源程序：

%%%%%%%%%%%%蚁群算法解决 TSP 问题%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
m = 50; %蚂蚁个数
Alpha = 1; %信息素重要程度参数
Beta = 5; %启发式因子重要程度参数
Rho = 0.1; %信息素蒸发系数
G = 200; %最大迭代次数
Q = 100; %信息素增加强度系数
C = [1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;...
    3238 1229;4196 1044;4312 790;4386 570;3007 1970;2562 1756;...
    2788 1491;2381 1676;1332 695;3715 1678;3918 2179;4061 2370;...
    3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;...
    3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;...
    2370 2975]; %31 个省会城市坐标
%%%%%%%%%%%%%%%第一步：变量初始化%%%%%%%%%%%%%%
n = size(C,1); %n 表示问题的规模(城市个数)
D = zeros(n,n); %D 表示两个城市距离间隔矩阵
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = ((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
        else
            D(i,j) = eps;
        end
        D(j,i) = D(i,j);
    end
end
Eta = 1./D; %Eta 为启发因子，这里设为距离的倒数
Tau = ones(n,n); %Tau 为信息素矩阵
Tabu = zeros(m,n); %存储并记录路径的生成
NC = 1; %迭代计数器
R_best = zeros(G,n); %各代最佳路线
L_best = inf.*ones(G,1); %各代最佳路线的长度
figure(1); %优化解
while NC <= G
    %%%%%%%%%%第二步：将 m 只蚂蚁放到 n 个城市上%%%%%%%%%%
    Randpos = [];
    for i = 1:(ceil(m/n))
        Randpos = [Randpos,randperm(n)];
    end
    Tabu(:,1) = (Randpos(1,1:m))';
    %%%第三步：m 只蚂蚁按概率函数选择下一座城市，完成各自的周游%%%%
    for j = 2:n
        for i = 1:m
            visited = Tabu(i,1:(j-1)); %已访问的城市
            J = zeros(1,(n-j+1)); %待访问的城市
            P = J; %待访问城市的选择概率分布
            Jc = 1;
            for k = 1:n
                if length(find(visited==k))==0
                    J(Jc) = k;
                    Jc = Jc+1;
                end
            end
            %%%%%%%%%%%计算待选城市的概率分布%%%%%%%%%%%
            for k = 1:length(J)
                P(k) = (Tau(visited(end),J(k))^Alpha)...
                    *(Eta(visited(end),J(k))^Beta);
            end
            P = P/(sum(P));
            %%%%%%%%%%%按概率原则选取下一个城市%%%%%%%%%
            Pcum = cumsum(P);
            Select = find(Pcum >= rand);
            to_visit = J(Select(1));
            Tabu(i,j) = to_visit;
        end
    end
    if NC >= 2
        Tabu(1,:) = R_best(NC-1,:);
    end
    %%%%%%%%%%%%%第四步：记录本次迭代最佳路线%%%%%%%%%%
    L = zeros(m,1);
    for i = 1:m
        R = Tabu(i,:);
        for j = 1:(n-1)
            L(i) = L(i)+D(R(j),R(j+1));
        end
        L(i) = L(i)+D(R(1),R(n));
    end
    L_best(NC) = min(L);
    pos = find(L==L_best(NC));
    R_best(NC,:) = Tabu(pos(1),:);
    %%%%%%%%%%%%%%%第五步：更新信息素%%%%%%%%%%%%%
    Delta_Tau = zeros(n,n);
    for i = 1:m
        for j = 1:(n-1)
            Delta_Tau(Tabu(i,j),Tabu(i,j+1)) = ...
                Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);
        end
        Delta_Tau(Tabu(i,n),Tabu(i,1)) = ...
            Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);
    end
    Tau = (1-Rho).*Tau+Delta_Tau;
    %%%%%%%%%%%%%%%第六步：禁忌表清零%%%%%%%%%%%%%
    Tabu = zeros(m,n);
    %%%%%%%%%%%%%%%%%历代最优路线%%%%%%%%%%%%%%%
    for i = 1:n-1
        plot([ C(R_best(NC,i),1), C(R_best(NC,i+1),1)],...
            [C(R_best(NC,i),2), C(R_best(NC,i+1),2)],'bo-');
        hold on;
    end
    plot([C(R_best(NC,n),1), C(R_best(NC,1),1)],...
        [C(R_best(NC,n),2), C(R_best(NC,1),2)],'ro-');
    title(['优化最短距离:',num2str(L_best(NC))]);
    hold off;
    pause(0.005);
    NC = NC+1;
end
%%%%%%%%%%%%%%%%%第七步：输出结果%%%%%%%%%%%%%%
Pos = find(L_best==min(L_best));
Shortest_Route = R_best(Pos(1),:); %最佳路线
Shortest_Length = L_best(Pos(1)); %最佳路线长度
figure(2),
plot(L_best)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')

4.2 蚁群算法求解二元函数极值

例 2   求函数 \(f (x，y) = 20 ( x^2 – y^2 )^2 – ( 1 – y )^2 – 3( 1 + y )^2 + 0.3\) 的最小值，其中 \(x\) 的取值范围为 \([–5，5]\)，\(y\) 的取值范围为 \([–5，5]\)。这是一个有多个局部极值的函数，其函数值图形如下图所示。

解：仿真过程如下：

（1）初始化蚂蚁个数 m = 20，最大迭代次数 G = 500，信息素蒸发系数 Rho = 0.9，转移概率常数 P0 = 0.2，局部搜索补偿 step = 0.1。

（2）随机产生蚂蚁初始位置，计算适应度函数值，设为初始信息素，计算状态转移概率。

（3）进行位置更新：当状态转移概率小于转移概率常数时，进行局部搜索；当状态转移概率大于转移概率常数时，进行全局搜索，产生新的蚂蚁位置，并利用边界吸收方式进行边界条件处理，将蚂蚁位置界定在取值范围内。

（4）计算新的蚂蚁位置的适应度值，判断蚂蚁是否移动，更新信息素。

（5）判断是否满足终止条件：若满足，则结束搜索过程，输出优化值；若不满足，则继续进行迭代优化。

适应度值进化曲线如下图所示，优化后的结果为 x = –5，y = 5，函数 f (x，y) 的最小值为–123.7。

蚁群算法求解二元函数极值MATLAB源程序：

%%%%%%%%%%%%%%蚁群算法求函数极值%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
m = 20; %蚂蚁个数
G = 500; %最大迭代次数
Rho = 0.9; %信息素蒸发系数
P0 = 0.2; %转移概率常数
XMAX = 5; %搜索变量 x 最大值
XMIN = -5; %搜索变量 x 最小值
YMAX = 5; %搜索变量 y 最大值
YMIN = -5; %搜索变量 y 最小值
%%%%%%%%%%%%%随机设置蚂蚁初始位置%%%%%%%%%%%%%%%%
for i = 1:m
    X(i,1) = (XMIN+(XMAX-XMIN)*rand);
    X(i,2) = (YMIN+(YMAX-YMIN)*rand);
    Tau(i) = func(X(i,1),X(i,2));
end
step = 0.1; %局部搜索步长
for NC = 1:G
    lamda = 1/NC;
    [Tau_best,BestIndex] = min(Tau);
    %%%%%%%%%%%%%计算状态转移概率%%%%%%%%%%%%%%%
    for i = 1:m
        P(NC,i) = (Tau(BestIndex)-Tau(i))/Tau(BestIndex);
    end
    %%%%%%%%%%%%%%%%位置更新%%%%%%%%%%%%%%%%%
    for i = 1:m
        %%%%%%%%%%%%局部搜索%%%%%%%%%%%%%%%%%
        if P(NC,i) < P0
            temp1 = X(i,1)+(2*rand-1)*step*lamda;
            temp2 = X(i,2)+(2*rand-1)*step*lamda;
        else
            %%%%%%%%%%%%全局搜索%%%%%%%%%%%%%%%%
            temp1 = X(i,1)+(XMAX-XMIN)*(rand-0.5);
            temp2 = X(i,2)+(YMAX-YMIN)*(rand-0.5);
        end
        %%%%%%%%%%%%%%%%边界处理%%%%%%%%%%%%%%%
        if temp1 < XMIN
            temp1 = XMIN;
        end
        if temp1 > XMAX
            temp1 = XMAX;
        end
        if temp2 < YMIN
            temp2 = YMIN;
        end
        if temp2 > YMAX
            temp2 = YMAX;
        end
        %%%%%%%%%%%%%%%判断蚂蚁是否移动%%%%%%%%%%%
        if func(temp1,temp2) < func(X(i,1),X(i,2))
            X(i,1) = temp1;
            X(i,2) = temp2;
        end
    end
    %%%%%%%%%%%%%%%%%更新信息素%%%%%%%%%%%%%%%
    for i = 1:m
        Tau(i) = (1-Rho)*Tau(i)+func(X(i,1),X(i,2));
    end
    [value,index] = min(Tau);
    trace(NC) = func(X(index,1),X(index,2));
end
[min_value,min_index] = min(Tau);
minX = X(min_index,1); %最优变量
minY = X(min_index,2); %最优变量
minValue = func(X(min_index,1),X(min_index,2)); %最优值
figure
plot(trace)
xlabel('搜索次数');
ylabel('适应度值');
title('适应度进化曲线')
%%%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%%%
function value = func(x,y)
value = 20*(x^2-y^2)^2-(1-y)^2-3*(1+y)^2+0.3;
end

5、蚁群算法的特点

蚁群算法是通过对生物特征的模拟得到的一种优化算法，它本身具有很多优点：

（1）蚁群算法是一种本质上的并行算法。每只蚂蚁搜索的过程彼此独立，仅通过信息激素进行通信。所以蚁群算法可以看作一个分布式的多智能体系统，它在问题空间的多点同时开始独立的解搜索，不仅增加了算法的可靠性，也使得算法具有较强的全局搜索能力。

（2）蚁群算法是一种自组织的算法。所谓自组织，就是组织力或组织指令来自于系统的内部，以区别于其他组织。如果系统在获得空间、时间或者功能结构的过程中，没有外界的特定干预，就可以说系统是自组织的。简单地说，自组织就是系统从无序到有序的变化过程。

（3）蚁群算法具有较强的鲁棒性。相对于其他算法，蚁群算法对初始路线的要求不高，即蚁群算法的求解结果不依赖于初始路线的选择，而且在搜索过程中不需要进行人工的调整。此外，蚁群算法的参数较少，设置简单，因而该算法易于应用到组合优化问题的求解。

（4）蚁群算法是一种正反馈算法。从真实蚂蚁的觅食过程中不难看出，蚂蚁能够最终找到最优路径，直接依赖于其在路径上信息素的堆积，而信息素的堆积是一个正反馈的过程。正反馈是蚁群算法的重要特征，它使得算法进化过程得以进行。

6、改进的蚁群算法

针对基本蚁群算法一般需要较长的搜索时间和容易出现停滞现象等不足，很多学者在此基础上提出改进算法，提高了算法的性能和效率。

6.1 精英蚂蚁系统

精英蚂蚁系统是针对基本蚁群系统算法的第一次改进，首先由 M. Dorigo 等人提出。该算法将已经发现的最好解称为 \(T^{bs}\)(best-so-far)，而该路径在修改信息素轨迹时，人工释放额外的信息素，以增强正反馈的效果。相应的信息素的修改公式为：

$$ \Delta \tau_{ij}= \sum_{k=1}^{m} \Delta \tau_{ij}^k + e \Delta \tau_{ij}^{bs}  \quad \text {(7)} $$

式中：\(e\) 是调整 \(T^{bs}\) 影响权重的参数；而 \(\Delta \tau_{ij}^{bs}\) 由下式给出：

$$\Delta \tau_{ij}^{bs} = \begin{cases} 1/L_{bs}, & \text{\((i,j) \in T^{bs}\)} \\ 0, & \text{其它} \\ \end{cases}    \quad \text {(8)} $$

其中 \(L_{bs}\) 是已知最优路径 \(T^{bs}\) 的长度。

6.2 最大最小蚂蚁系统

为了克服基本蚁群系统中可能出现的停滞现象，Thomas Stutzle 等人提出了最大 - 最小（MAX-MIN）蚁群系统，主要有三方面的不同：

（1）与蚁群系统相似，为了充分利用循环最优解和目前为止找出的最优解，在每次循环之后，只有一只蚂蚁进行信息素更新。这只蚂蚁可能是找出当前循环中最优解的蚂蚁（迭代最优的蚂蚁），也可能是找出从实验开始以来最优解的蚂蚁（全局最优的蚂蚁）；而在蚂蚁系统中，对所有蚂蚁走过的路径都进行信息素更新。

（2）为避免搜索的停滞，在每个解元素（TSP 中是每条边）上的信息素轨迹量的值域范围被限制在\([ \tau_{min}，\tau_{max}]\)区间内；而在蚂蚁系统中信息素轨迹量不被限制，使得一些路径上的轨迹量远高于其他边，从而蚂蚁都沿着同条路径移动，阻止了进一步搜索更优解的行为。

（3）为使蚂蚁在算法的初始阶段能够更多地搜索新的解决方案，将信息素初始化为 \( \tau_{max}\)；而在蚂蚁系统中没有这样的设置。

6.3 基于排序的蚁群算法

基于排序的蚁群算法（Rank-Based Ant System）是 Bullnheimer、Hartl 和 Strauss 等人提出的。在该算法中，每个蚂蚁释放的信息素按照它们不同的等级进行挥发，另外类似于精英蚁群算法，精英蚂蚁在每次循环中释放更多的信息素。在修改信息素路径前，蚂蚁按照它们的旅行长度进行排名（短的靠前），蚂蚁释放信息素的量要和蚂蚁的排名相乘。在每次循环中，只有排名前 \(w-1\) 位的蚂蚁和精英蚂蚁才允许在路径上释放信息素。己知的最优路径给以最强的反馈，和系数 w 相乘；而排名第 r 位的蚂蚁则乘以系数\(“w-r”（ \geq 0）\)。信息素如下式所示：

$$ \Delta \tau_{ij}= \sum_{r=1}^{w-1} (w-r) \Delta \tau_{ij}^r + w \Delta \tau_{ij}^{bs}  \quad \text {(9)} $$

$$\Delta \tau_{ij}^r = \begin{cases} 1/L_r, & \text{\((i,j) \in T^r\)} \\ 0, & \text{其它} \\ \end{cases}    \quad \text {(10)} $$

式中，\(L_r\) 是排名为第 \(r\) 位的蚂蚁的旅行路径的长度。

6.4 自适应蚁群算法

基本蚁群系统让信息量最大的路径对每次路径的选择和信息量的更新起主要作用，但由于强化了最优信息反馈，就可能导致“早熟”停滞现象。而最大最小蚁群算法将各个路径上的信息量的更新限定在固定的范围内，这虽然在一定程度上避免了“早熟”停滞现象，但在解分布较分散时会导致收敛速度变慢。以上方法的共同缺点在于：它们都按一种固定不变的模式去更新信息量和确定每次路径的选择概率。

为了克服以上算法的不足，L. M. Gambardella 和 M. Dorigo 提出了基于调节信息素挥发度的自适应蚁群算法。相对基本蚁群算法的改进如下：

（1）在每次循环结束后求出最优解，并将其保留。

（2）自适应地改变 ρ 值。当问题规模比较大时，由于信息量的挥发系数 ρ 的存在，使那些从未被搜索到的信息量会减小到接近于 0，降低了算法的全局搜索能力；当 ρ 过大且解的信息量增大时，以前搜索过的解被选择的可能性过大，也会影响到算法的全局搜索能力；通过减小 ρ 虽然可以提高算法的全局搜索能力，但又会使算法的收敛速度降低。因此可以自适应地改变ρ的值。ρ的初始值\(\rho(t_0)=1\)；当算法求得的最优值在 N 次循环内没有明显改进时，ρ 减为：

$$\rho(t) = \begin{cases} 0.95 \rho (t-1), & \text{当\(0.95 \rho (t-1) \geq \rho_{min}\)时} \\ \rho_{min}, & \text{其它} \\ \end{cases}    \quad \text {(11)} $$

式中：\(\rho_{min}\) 为 ρ 的最小值，它可以防止 ρ 过小而降低算法的收敛速度。