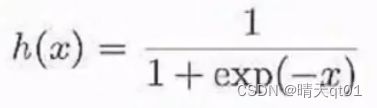【机器学习算法】神经网络与深度学习-2 由感知机到BP神经网络的内容
目录
BP神经网络(里程碑)
神经元的组成1:组合函数(combination function)
神经元的组成2:激活函数(activation function)
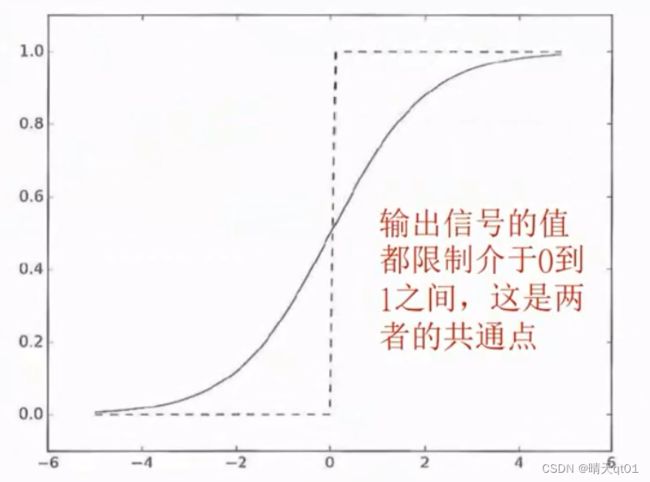
Sigmoid与step 函数的区别与共同点
输出层的设计
我的主页:晴天qt01的博客_CSDN博客-数据分析师领域博主
目前进度:第四部分【机器学习算法】
BP神经网络(里程碑)
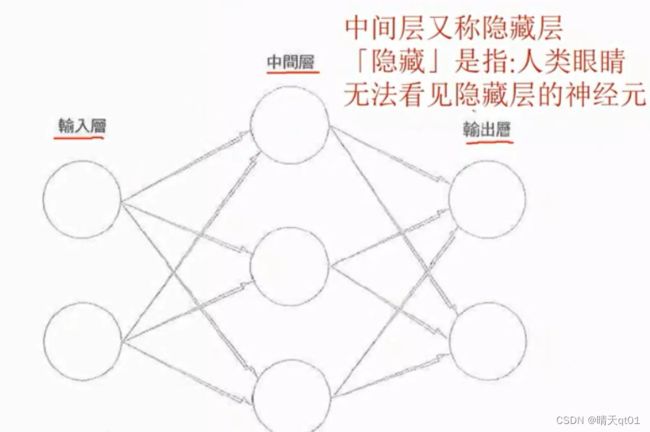
上次我们已经学了感知机,它由输入层,中间层(隐藏层),输出层构成
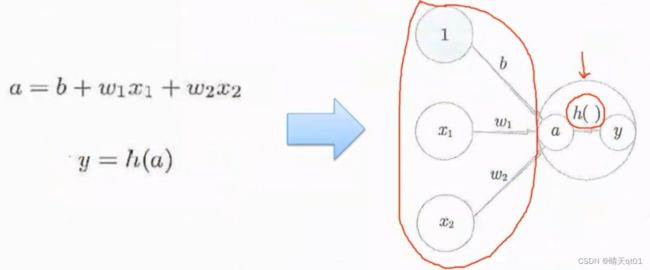
我们之前感知机有3个参数组成,可以我们把它表示出来,这里面没有显示偏置项(界限),只是把它当成系数。
我们还能把它表示为右边的形式。把偏置项看作一个输入项,输入的值为常数1,权重为b。我们BP神经网络会以这种形式表达。
其实我们还能对这个公式再进行一定程度的修改简化。
我们把y进行一系列的处理,就可以得到右下的3个公式,用它可以代表左上角的公式。
这里的h(a)代表的就是激活函数,一会我们会介绍不同的激活函数。也就是我们把感知机它加总的结果(包括偏置项b)通过激活函数h()就得到y
神经元的组成1:组合函数(combination function)
我们就得到了BP神经网络的表示方式
在这里面,a是吧输入字段进行了一个组合,我们也可以把它视为一个函数,叫组合函数。
组合函数的结果,我们在把它代入到激活函数h()之后,输出。
所以在神经网络中,我们会把感知机的表达方式这样表达后进行输出。
神经元的组成2:激活函数(activation function)
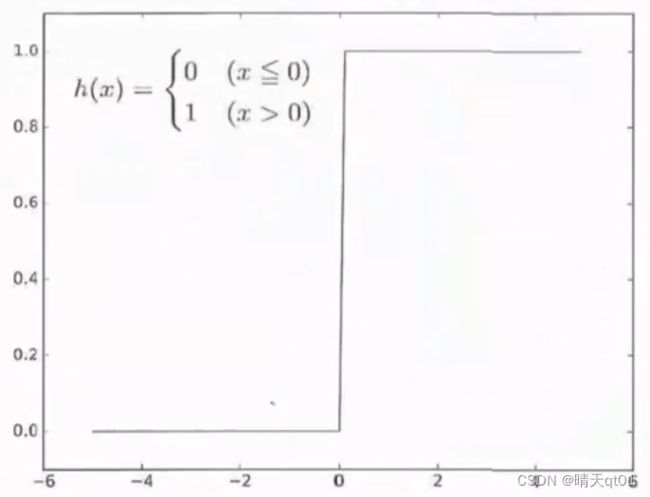
在这里,我们的激活函数就是一个阶梯函数,它只要小于等于0那么他就是0,它大于0时立马就变成1,之间没有过度。
这种以临界值来作为分隔转换输出的函数,称为阶梯函数(step function)
这是感知机使用的激活函数。其他时候我们用得到阶梯函数不同。
各神经网络的激活函数:
Step Function——》感知机使用
Sigmoid Function——》BP神经网络使用
ReLU Function——》深度学习使用
这里大家可能会有疑惑,为什么我们不沿用感知机的阶梯函数,主要原因是因为阶梯函数是不可微分的,而我们拥有神经网络的架构之后,我们要得到最优的权重比例,是需要利用微分的知识进行优化的,这个之前也说了一部分。
如果我们使用的是阶梯函数,就不能通过机器的计算来得到最接近现实值的函数。所以就要人为给定数值,我们希望机器能自动学习到这个参数。
它这个函数它永远不会到1或者永远不会到-1.它介于0-1之间。它是一个连续型的函数,它可微分,step function不能微分。
但是这个到深度学习的时候,就不在适用了,因为深度学习是有非常多的隐藏层sigmoid function会造成梯度消失,或者梯度爆炸的问题,不能有效的学到权重值。深度学习就会ReLU这个激活函数来解决这两个问题。这个问题我们一会细说。
Sigmoid与step 函数的区别与共同点
首先sigmoid是平滑的函数, 针对输入产出连续性的输出。而step是有明确界限的,明确改变输出
学习神经网络的时候sigmoid的平滑是有非常重要的意义存在。
感知机传递的是0或1的这两个值信号。是连续性的实数信号。
Sigmoid与step函数的共同点:
二者都是非线性函数,sigmoid是曲线,step是像楼梯一样曲折的直线,因此都归类到非线性函数。
线性函数用算式表示为h(x)=cx,线性函数是直线
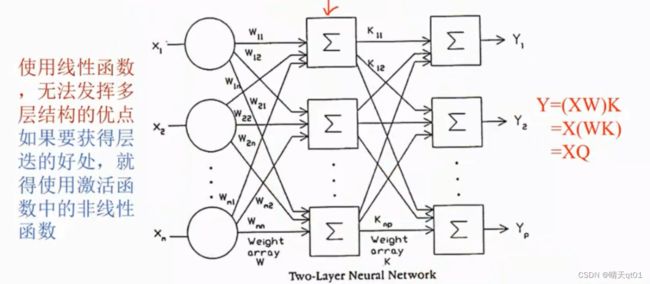
神经网络必须使用非线性函数来作为激活函数,如果使用的是线性函数,那么神经网络的层数就毫无意义了。增加层数也不会增加它的学习能力
也就是说隐藏层用一层和用多层都是一样的结果。
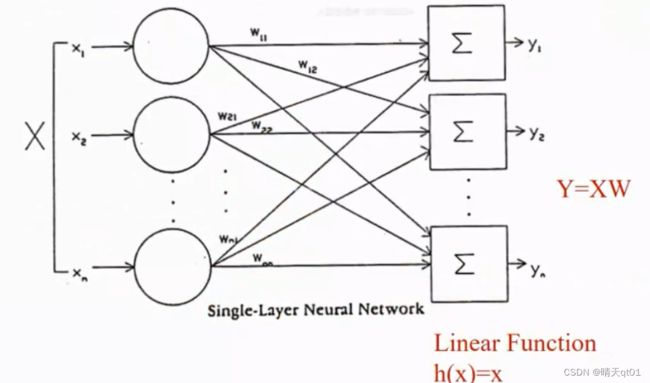
案例:只有组合函数
这图是把组合函数的结果直接输出。我们Y的结果就是X*W的结果。选择我们增加隐藏层
这个时候会产生一个新矩阵Q,它的含义就是回到没有隐藏层的情况,
所以我们的激活函数尽量不要使用线性函数,这样会导致多层结构的效果被消耗。不能提升计算能力
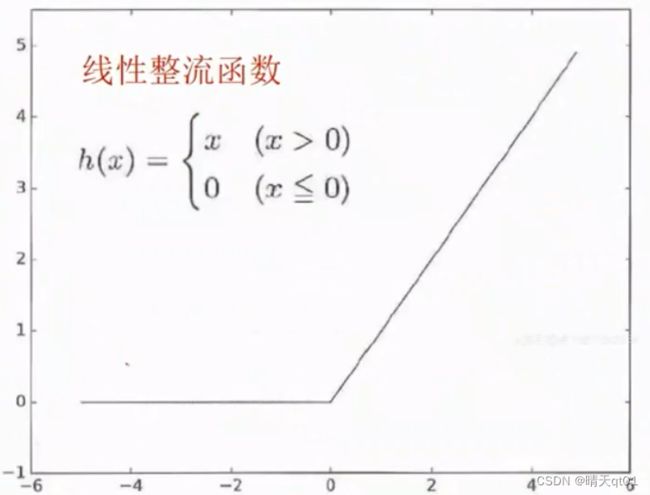
激活函数ReLU(rectified Linear Unit)
当x小于0的时候我们就输出0,当x大于0的时候就输出x,这里就有点像阶梯函数组合线性函数。这种函数是非线性,被叫做线性整流函数。因为它是非线性,所以多层结果可以优化效果,而且是可微分的。在异常层数增加的时候,它也不会有sigmoid梯度消失或者梯度爆炸的问题。所以深度学习才会使用这个激活函数。
输入层组合函数一般就是求和。
输出层的设计
神经网络可以用来解决分类问题与回归问题。
但解决分类问题或回归问题时,必须改变输出层的激活函数,不同的问题对应不同的激活函数。
回归问题可以采用恒等函数(h(x)=x)或sigmoid函数,
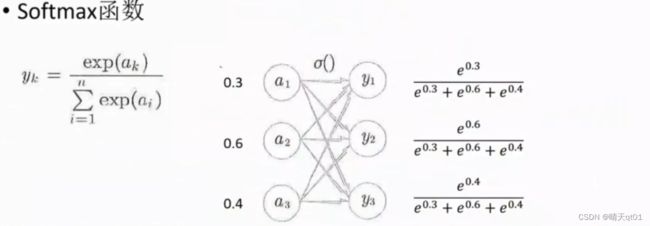
分类问题,如果是用softmax(分多类)或者sigmoid函数(分两类)
Softmax会保证结果的总和为1.
都是以e为底的指数,分母是各自以e为底的指数。所以它相加的总和一定为1.
把所有的组合函数都拿来计算。