【学习笔记】PyTorch（1）神经网络入门

神经网络

利用torch.nn包来构建神经网络，其训练过程大致包括以下几点：

1. 定义一个包含可训练参数的神经网络；
2. 迭代整个输入；
3. 通过神经网络前向传播处理输入；
4. 利用优化器计算损失（loss）；
5. 反向传播梯度到神经网络的参数；
6. 更新训练的参数；

1 神经网络各层

神经网络通常包含有：

1. 卷积层 Convolution Layer；
2. 池化层 Pooling Layer；
3. 非线性激活层 Non-linear Activation Layer；
4. 线性激活层 Linear Layer；

很多层和函数都可以在torch.nn.functional 和nn.Module中直接调用，什么时候使用nn.Module，什么时候使用nn.functional呢？
一般情况下，如果模型有可学习的参数(如卷积层、全连接层)，最好用nn.Module；其他情况(激活函数，损失函数)nn.functional相对更简单一些。

1.1 卷积层

在输入矩阵外填充padding圈0，卷积核在输入矩阵上以stride为步长移动，对应位置元素相乘再相加，得到新的特征图。

• conv

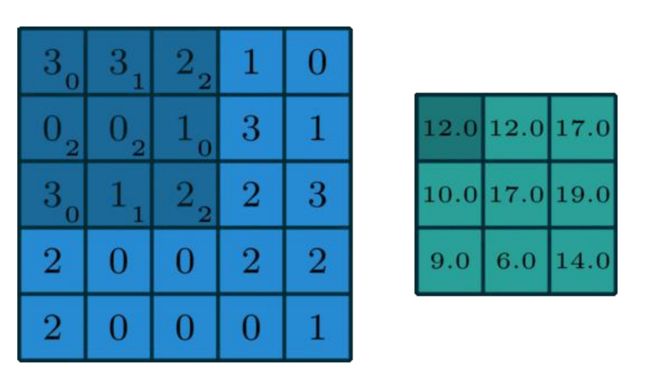
卷积的手动实现

import torch
from torch import nn
def corr2d(X,K):
    """二维卷积"""
    xh,xw = X.shape
    kh,kw = K.shape
    Y = torch.zeros((xh - kh + 1,xw - kw + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i][j] = (X[i:i+kh,j:j+kw] * K).sum()
    return Y


class Conv2D(nn.Module):
	"""加入可调参数"""
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

• padding

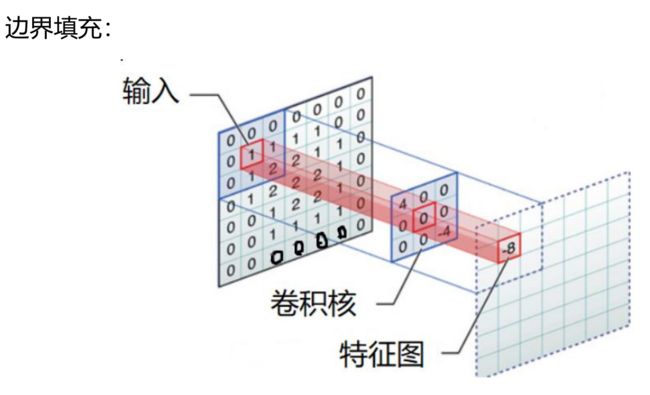
• stride

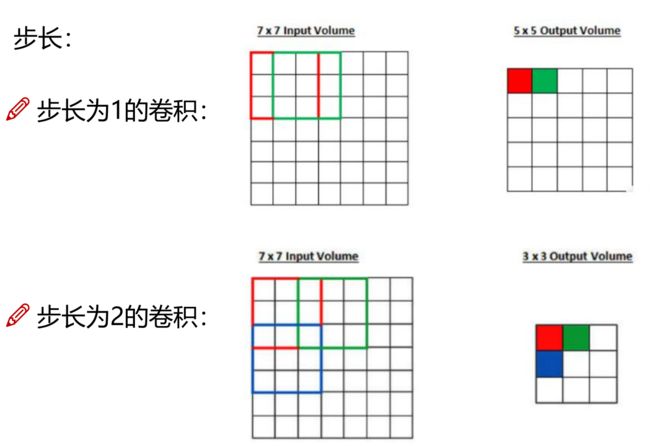
设输入图像的宽度和长度分别为W1、H1，F为卷积核长和宽、P为边界填充(加几圈0)，S为滑动窗口步长。输出特征图的宽度和长度分别为W2、H2，其计算公式如下：

eg:

卷积层用torch.nn.functional实现

import torch.nn.functional as F
import torch

# convolution layer
input = torch.Tensor([[[1,1,2,2,1],
                      [1,1,1,2,1],
                      [2,1,1,0,2],
                      [2,1,0,1,2],
                      [2,1,2,2,2]],
                      [[0,1,2,0,1],
                      [2,2,1,1,0],
                      [2,1,0,0,2],
                      [1,0,0,0,2],
                      [0,1,0,1,2]],
                      [[2,2,0,1,2],
                      [0,0,2,1,2],
                      [2,1,0,2,1],
                      [1,1,0,0,0],
                      [0,0,1,1,1]]])
print(input.shape)

kernel = torch.Tensor([[[1,1,1],
                       [-1,-1,0],
                       [-1,1,0]],
                       [[-1,-1,-1],
                       [-1,1,0],
                       [-1,1,0]],
                       [[1,0,-1],
                       [0,0,0],
                       [1,-1,-1]]])   
# 变换尺寸
input = torch.reshape(input,(1,3,5,5))   
kernel = torch.reshape(kernel,(1,3,3,3))

# conv2d二维卷积
output = F.conv2d(input,kernel)
print('stride=1;padding=0时的卷积结果：')
print(output)

# 卷积步长为2
print('stride=2;padding=0时的卷积结果：')
output2 = F.conv2d(input,kernel,stride=2)
print(output2)

# 卷积步长为2；边界填充1圈0；偏置为1
bias = torch.tensor([1])
print('stride=2;padding=1；bias=1时的卷积结果：')
output3 = F.conv2d(input,kernel,bias,stride=2,padding=1)
print(output3)

结果：

stride=1;padding=0时的卷积结果：
tensor([[[[ 0., -2., -7.],
[-10., -4., 2.],
[ -2., -3., -1.]]]])
stride=2;padding=0时的卷积结果：
tensor([[[[ 0., -7.],
[-2., -1.]]]])
stride=2;padding=1；bias=1时的卷积结果：
tensor([[[[ 3., -5., -4.],
[ 0., -3., 7.],
[ 0., 0., -1.]]]])

1.2 池化层

池化层进行下采样，可以减小计算量，防止过拟合。有最大池化（MaxPool）和平均池化（AvgPool），一般采用最大池化。

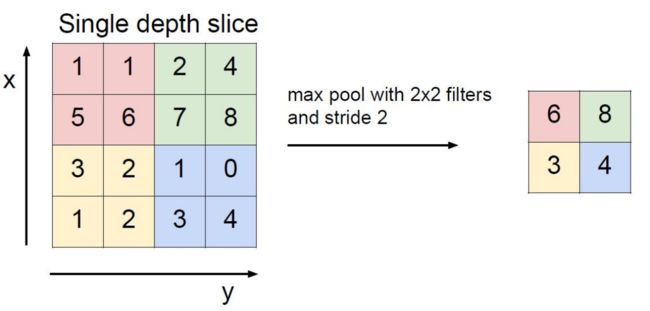
池化手动实现

def pool2d(X, pool_size, mode='max'):
	'''池化：mode='max';mode='avg' '''
    p_h, p_w = pool_size
    Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
    return Y

池化层用torch.nn.functional实现

import torch.nn.functional as F
import torch

# convolution layer
input = torch.Tensor([[1,1,2,4],
                      [5,6,7,8],
                      [3,2,1,0],
                      [1,2,3,4]])

# 变换尺寸
input = torch.reshape(input,(1,1,4,4))   

output = F.max_pool2d(input,2)#默认stride=kernel_size；此处默认stride=2
print(output)

结果：

tensor([[[[6., 8.],
[3., 4.]]]])

• 池化层和卷积层类似，都有stride和padding，但没有可以学习的参数；
• 输入通道数=输出通道数。

1.3 非线性激活层

没有激活函数的每层都相当于矩阵相乘，都是线性变换。非线性激活层给神经网络引入了非线性，常用的非线性激活函数有Sigmoid、Tanh、ReLU、Softmax等。

import torch
import torch.nn.functional as F
input = torch.tensor([[1,-0.5],
                      [-1, 3]])
print(input)
output = F.relu(input)
print('经过relu后：')
print(output)

结果：

tensor([[ 1.0000, -0.5000],
[-1.0000, 3.0000]])
经过relu后：
tensor([[1., 0.],
[0., 3.]])

1.4 线性层

线性层又称全连接层，每个神经元实现与上一层所有神经元链接，实现对前一层的线性组合。

import torch
import torch.nn.functional as F
input = torch.tensor([[1,2,3]])
print(input.shape)
weight = torch.tensor([[1,2,3,4],
                       [1,2,3,4],
                       [1,2,3,4]])
print(weight.shape)

output = F.linear(input,weight.T)
print('经过linear后：')
print(output)

结果：

torch.Size([1, 3])
torch.Size([3, 4])
经过linear后：
tensor([[ 6, 12, 18, 24]])

2 定义简单的神经网络

定义网络时需要继承nn.Module类，在 __init__函数里定义网络的各层，在forward函数中进行前向传播。

# 导入模块
import torch
from torch.nn import ReLU

input = torch.tensor([[1,-0.5],
                      [-1, 3]])
input = torch.reshape(input,(-1,1,2,2))

class Model(nn.Module):#继承Module类
    def __init__(self) -> None:
        super(Model,self).__init__()
        #定义网络各层
        self.relu1 = ReLU()

    # 前向传播函数
    def forward(self,input): 
        output = self.relu1(input)#调用定义的网络层
        return output

model = Model()#实例化模型
print('模型：')
print(model)
print('输入：')
print(input)
output = model(input)#用模型迭代输入
print('输出：')
print(output)

结果：

模型：
Model(
(relu1): ReLU()
)
输入：
tensor([[[[ 1.0000, -0.5000],
[-1.0000, 3.0000]]]])
输出：
tensor([[[[1., 0.],
[0., 3.]]]])

• 可以用Sequential()简化模型定义

from torch import nn 
from torch.nn import Conv2d,MaxPool2d,Flatten,Linear,Sequential,L1Loss
import torch
from torch.utils.tensorboard import SummaryWriter

class Model(nn.Module):
    def __init__(self) -> None:
        super(Model,self).__init__()
        # self.conv1 = Conv2d(3,32,5,padding=2)#64*32*32*32
        # self.maxpool1 = MaxPool2d(2)#64*32*16*16
        # self.conv2 = Conv2d(32,32,5,padding=2)#64*32*16*16
        # self.maxpool2 = MaxPool2d(2)#64*32*8*8
        # self.conv3 = Conv2d(32,64,5,padding=2)#64*64*8*8
        # self.maxpool3 = MaxPool2d(2)#64*64*4*4
        # self.flatten = Flatten()#64*1024
        # self.linear1 = Linear(1024,64)#64*64
        # self.linear2 = Linear(64,10)#64*10

        self.model1 = Sequential(
            Conv2d(3,32,5,padding=2),
            MaxPool2d(2), 
            Conv2d(32,32,5,padding=2), 
            MaxPool2d(2), 
            Conv2d(32,64,5,padding=2), 
            MaxPool2d(2), 
            Flatten(), 
            Linear(1024,64),
            Linear(64,10)
        )
    
    def forward(self,x):
        # x = self.conv1(x)
        # x = self.maxpool1(x)
        # x = self.conv2(x)
        # x = self.maxpool2(x)
        # x = self.conv3(x)
        # x = self.maxpool3(x)
        # x = self.flatten(x)
        # x = self.linear1(x)
        # x = self.linear2(x)
        x = self.model1(x)
        return x

model = Model()
print(model)

input = torch.ones((64,3,32,32))
print(input.shape)
output = model(input)
print(output.shape)

结果：

Model(
(model1): Sequential(
(0): Conv2d(3, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(2): Conv2d(32, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(3): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(4): Conv2d(32, 64, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(5): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(6): Flatten(start_dim=1, end_dim=-1)
(7): Linear(in_features=1024, out_features=64, bias=True)
(8): Linear(in_features=64, out_features=10, bias=True)
)
)
torch.Size([64, 3, 32, 32])
torch.Size([64, 10])

3 反向传播

3.1 损失函数

损失函数用于计算实际输出和目标之间的差距、为反向传播更新输出提供一定的依据。回归问题中常用损失函数为均方误差MSE、MAE等，分类问题中常用交叉熵Cross-Entropy。

import torch
from torch.nn import L1Loss,MSELoss

inputs = torch.tensor([1,2,3],dtype=torch.float32)
targets =torch.tensor([1,2,5],dtype=torch.float32)

loss = L1Loss()#2/3
result = loss(inputs,targets)

loss_mse = MSELoss()#4/3
result_mse = loss_mse(inputs,targets)

print(result)
print(result_mse)

结果：

tensor(0.6667)
tensor(1.3333)

3.2 优化器

优化器可以对模型参数进行优化，使得的损失最小化，通常是对于梯度进行优化。常见的优化器有BGD、SGD、MBGD、Adam。

from torch import nn 
from torch.utils.data import DataLoader
import torchvision
from torch.nn import Conv2d,MaxPool2d,Flatten,Linear,Sequential,L1Loss
import torch

# 加载数据集CIFAR10
dataset = torchvision.datasets.CIFAR10("./dataset",train=False,                               transform=torchvision.transforms.ToTensor(),download=True)
#构建数据集
dataloader = DataLoader(dataset,batch_size=1)
#定义模型
class Model(nn.Module):
    def __init__(self) -> None:
        super(Model,self).__init__()
        #定义网络各层
        self.model1 = Sequential(
            Conv2d(3,32,5,padding=2),
            MaxPool2d(2), 
            Conv2d(32,32,5,padding=2), 
            MaxPool2d(2), 
            Conv2d(32,64,5,padding=2), 
            MaxPool2d(2), 
            Flatten(), 
            Linear(1024,64),
            Linear(64,10)
        ) 
    def forward(self,x):
        x = self.model1(x)
        return x
        
# 损失函数        
loss = nn.CrossEntropyLoss()
#模型实例化
model = Model()

#设置优化器
optim = torch.optim.SGD(model.parameters(),lr=0.01)

开始训练
for epoch in range(20):
    running_loss = 0.0
    for data in dataloader:
        imgs,targets = data#获取数据
        outputs = model(imgs)#用模型遍历数据
        result_loss = loss(outputs,targets)#计算损失
        optim.zero_grad()#梯度清零
        result_loss.backward()#反向传播
        optim.step()#更新参数
        # print(result_loss)
        running_loss += result_loss
        print(running_loss)

参考：

视频教程1
视频教程2
视频教程3