DL-based 多模态医学图像配准

基于深度学习的多模态医学图像配准

---

参考文献

• Unsupervised Multi-Modal Medical Image Registration via Discriminator-Free Image-to-Image Translation. IJCAI, 2022

Abstrct

在临床实践中，对齐良好的多模态图像，如磁共振（Magnetic Resonance，MR）和计算机断层扫描（Computed Tomography，CT），可以为图像引导治疗提供补充信息。多模态图像配准对于融合这些图像信息至关重要。然而，由于不同模态之间复杂且未知的空间对应关系，这仍然是一项非常具有挑战性的任务。

Introduction

基于学习的配准通过最大化预定义的相似性度量，寻求直接从一对图像预测变形场 [Fan等人，2019]¹。监督或半监督学习策略在训练阶段使用真实变形场或分割掩码，可能面临缺乏标注数据的问题 ²。

即使对于专家来说，标注配准数据也是非常耗时和费力的，因此提出了无监督方法来克服这一限制，神经网络仅通过最大化目标图像和源图像之间的图像相似性来预测配准变形场。

然而，无监督方法的性能在很大程度上取决于相似性度量的选择。常见的相似性度量，如 MSE 和 NCC，非常适合于单模态配准问题 [Balakrishnan等人，2019；de V os等人，2017]，但在多模态环境中表现不佳。通常，无监督多模态配准方法使用归一化互信息（NMI）和模态独立邻域描述符（MIND）作为图像相似性度量。

然而，NMI 作为一种全局度量，仅测量两幅完整图像之间的统计相关性，因此很难将其用于局部图像对齐。另一方面，MIND 是一种 patch-based 的图像相似性度量，往往会导致严重的图像变形，无法实现全局对齐。

鉴于最近多模态图像转换的成功 [Huang等人³；Park等人⁴]，解决多模态配准的另一种解决方案是使用图像到图像（image-to-image，I2I）转换框架将问题转换为更简单的单模态任务 [Qin等人⁵]。具体来说，基于转换的方法使用 GAN 将图像从源模态转换为目标模态。

然而，这种基于 GAN 的图像转换往往会生成形状不一致的结果和额外的人工解剖特征，这反过来会恶化配准性能 [Arar等人⁶；Xu等人⁷]。更具体地说，由于成像床的形状、扫描仪的成像协议和视野，不同的模态具有非常明显的几何差异。我们将这些差异称为 domain-specific deformations 特定于域的变形 [Wang等人⁸]。

我们认为，不一致性和伪影是由鉴别器引入的，鉴别器错误地将特定于域的变形编码为不可或缺的外观特征，并鼓励生成器再现变形。这往往会给配准任务带来不必要的困难。本文表明，通过去除 I2I 中的鉴别器，可以提高多模态图像配准的性能。

Method

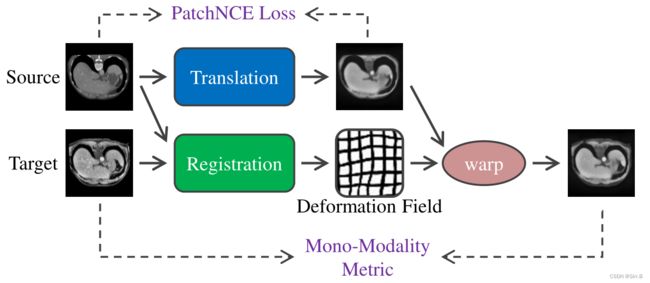
我们的基于模态转换的配准方法学习了跨模态转换，即两种模态之间的映射，从而能够使用单模态度量来训练配准网络。源图像被变形场扭曲以与目标图像对齐。我们使用 PatchNCE 损失来鼓励转换网络保留对象的结构特征。并将像素损失设计为单模态度量，像素损失不仅可以度量转换网络的外观迁移效果，还可以度量配准图像的不同程度，因此可以同时训练转换网络和配准网络。

Loss Functions

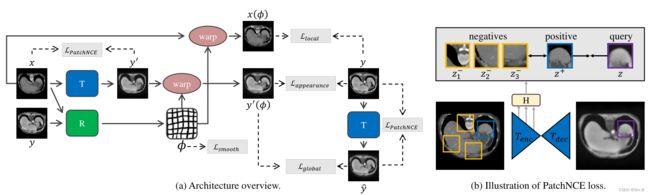
我们的模型由两个部分组成：配准网络 $R$ 和无判别器转换网络 $T$。这两个网络以端到端的方式联合训练。在我们的上下文中，像素损失 $L_{appearance}$ 是在目标模态中计算的单模态度量。基于图 1 所示的架构，我们添加了两个新的损失项 $L_{local}$ 和 $L_{global}$，以实现 $x(\varphi )$ 和 $y$ 之间的局部和全局对齐。

其中，
$L_{global}$ = $L_1\text{-norm}$ = ${\mathcal{L}}_{\text{appearance }}(T,R)={\Vert y^{\prime }(\varphi )-y\Vert }_1$；
$L_{local}=PatchNCE$；
$L_{smooth}=L_2\text{-nrom}={\sum }_{u\in N(v)}\Vert \varphi (u)-\varphi (v){\Vert }_2$，其中，$N(v)$ 表示与像素 $v=(i,j)$ 相邻的一组像素。

在预测时，只需要向配准网络中输入源图像和固定图像，就能得到合适的变形场用于配准。由于使用 I2I，都是把3D图像切片成2D才输入网络，因此预测的变形场是2D变形场。

我们的代码位于 heyblackC/DFMIR 。

Related Methods

弱监督学习

在弱监督训练方案下，只需要在训练阶段使用分割图。这类方法可以直接输入 3D 图像并得到结果。^{2 9}

使用 MIND 等多模态图像强度相似度量学习

PDD 2.5

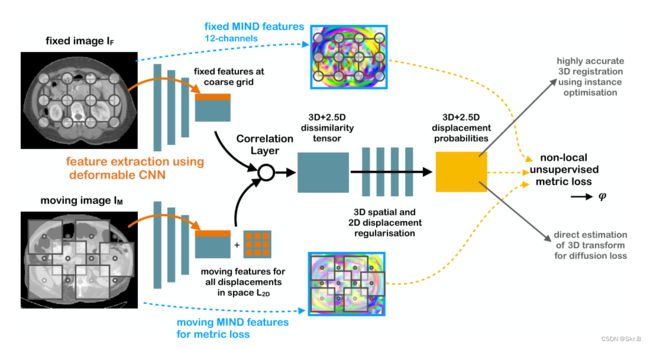
Weakly-supervised learning of multi-modal features for regularised iterative descent in 3D image registration¹⁰

使用仿射矩阵的一致性正则学习¹¹

或者，可以采用分割标签进行弱监督，主要是最大限度地利用专家标注对齐已知结构^{2 10}。这可以更好地配准具有良好代表性的解剖结构，但可能会对无标签的区域产生偏见并恶化性能。

为了避免对所有相关解剖结构进行详细全面的标注，并避免标签偏差，无监督和基于度量的配准网络被广泛用于基于单模态配准学习。然而，这对多模态配准问题提出了另一个挑战，因为目前尚未开发出通用度量，必须在使用局部对比度不变边缘特征（如 NGF、LCC）和 MIND 或更多全局统计度量（如互信息）之间进行权衡。基于度量的方法还难以调整超参数，以平衡相似性度量的权重（确保固定图像和配准的浮动图像之间的相似性）和正则化权重（确保合理的变形）。

为了避免多模图像配准相似性度量的困难，我们提出了一个全新的概念。我们的方法既不需要标签监督，也不需要 handcrafted 的相似度量。

• 我们将自己局限于刚性配准，目的是通过最小化一致性差异来学习 CT 和 MRI 之间的多模态配准，而无需度量监督。
• 我们使用 CNN 进行特征提取，每个模态最初有单独的编码器块，然后在最后一层中共享权重。
• 我们使用一个没有可训练权重的相关层和一个可微最小二乘拟合程序来寻找最佳的三维刚性变换。

我们提出了用于多模态图像配准的自监督学习方法，旨在最小化变换矩阵一致性差异。在每次训练迭代中，使用一个（已知）随机刚性变换矩阵 ${\text{R}}_{23}$ 生成合成图像。这样，得到了由两个多模态变换（变换矩阵 ${\text{R}}_{21}$ 和 ${\text{R}}_{31}$）和一个已知单模态变换（变换矩阵 ${\text{R}}_{23}$）组成的循环，从而通过 $|{\text{R}}_{23}\cdot {\text{R}}_{31}-{\text{R}}_{21}|\to \text{min}$ 的最小化问题指导神经网络学习。

乍一看，使用如此微弱的损失函数指导网络学习似乎很大胆（On first sight, it might seem daring to use such a weak guidance.）？但一旦学习到合适的特征，损失项就可以收敛，因为满足了一致性约束。我们主要依赖随机性（通过生成多个大型随机刚性变换矩阵）和神经网络探索性学习的力量。。。

在对应解剖结构中嵌入点坐标来学习

SAME: Deformable Image Registration based on Self-supervised Anatomical Embeddings ¹²
SAM: Self-supervised Learning of Pixel-wise Anatomical Embeddings in Radiological Images ¹³

SAM

放射学图像，如 CT 和 X 射线，呈现具有内在结构的解剖学。能够在不同的图像中可靠地定位相同的解剖结构是医学图像分析的一项基本任务。原则上，可以使用地标检测（landmark detection）或语义分割来完成这项任务，但要需要为 ROI 解剖结构提供大量标注数据。

我们介绍了一种称为自监督解剖嵌入（Self-supervised anatomical embedding，SAM）的方法，从无标注的图像中学习内在结构。SAM 为描述其解剖位置或身体部位的每个图像像素生成语义嵌入。为了产生这种嵌入，我们提出了一个像素级的对比学习框架。从粗到精的策略确保对全局和局部解剖信息进行编码。设计了负样本选择策略以增强嵌入的可分辨性。

使用 SAM，可以在模板图像上标记任意关注点，然后通过简单的最近邻搜索在其他图像中定位相同的身体部位。我们证明了 SAM 在 2D 和 3D 图像的多任务中的有效性。在具有 19 个标志点的胸部 CT 数据集上，SAME ¹² 优于广泛使用的配准算法，而推理只需要 0.23 秒。

SAME

SAM 旨在匹配稀疏点。通过匹配固定图像和运动图像之间的每个像素，可以直接将其用于全体积配准，但由于三维 CT 扫描中有数百万像素，因此效率极低。我们提出了一种 SAM-Enhanced 可变形配准算法，称为 SAME ¹²。

SAME 包括三个步骤:

• SAM-affine。我们首先在固定图像上采样稀疏网格并丢弃身体外的点，然后使用 SAM 匹配运动图像上相应的点。保持相似度分数高于阈值的匹配。利用这些点对，可以通过简单的最小二乘拟合来估计仿射变换矩阵。
• SAM-coarse，使用 SAM 在前一步的仿射配准图像上计算新的对应网格，以插值粗变形场。这两个步骤非常有效，不需要额外的训练，并且可以为最后一个步骤提供良好的初始化。
• 最后，SAM-VoxelMorph，通过结合基于 SAM 的相关特征和额外的基于 SAM 的相似性损失，增强了基于深度学习的 VoxelMorph 配准方法。这是无监督的，只需要预训练的 SAM 模型。

虽然 SAM loss 是更具语义对齐图像的有效手段，但在标准体素变形中提取的特征仍然缺乏语义信息，这可能需要更好地指导预测。相关特征最初是在 FlowNet 中提出的，用于处理光流的这个问题。PDD-Net 中也使用它进行配准。简而言之，它计算 $X_f$上像素 $u$ 和 $X_m$上像素 $u+d$ 的相似性，其中 $d$ 是一个小位移。计算每个像素和 n 个可能的位移值的相似性，以生成 n 通道特征图，然后在网络中的某个点将其连接到原始特征图。

当使用 SAM 时，两个像素的语义相似性可以简单地计算为两个 SAM 向量的内积，${\mathcal{L}}_{SAM}\left(S_f,S_m^v\right)=\frac{1}{|\Omega |}{\sum }_{\mathbf{u}\in \Omega }⟨S_f(\mathbf{u}),S_m^v(\mathbf{u})⟩$。其中，$\Omega$ 是 mask 中所有像素的集合；上标 $v$ 表示已被 SAM 体素变形预测的变形场扭曲。

我们根据经验发现，使用 27 个位移值 $d\in \{-2,0,2{\}}^3$ 产生了良好的结果。在预测变形时，注入 SAM 相关特征为网络提供了改进的线索，从而进一步提高了准确性。

---

1. Jingfan Fan, Xiaohuan Cao, Qian Wang, PewThian Yap, and Dinggang Shen. Adversarial learning for monoor multi-modal registration. Medical image analysis, 58:101545, 2019. ↩︎

2. Hu, Y .; Modat, M.; Gibson, E.; Li, W.; Ghavami, N.; Bonmati, E.; Wang, G.; Bandula, S.; Moore, C.M.; Emberton, M.; et al. Weakly-supervised convolutional neural networks for multimodal image registration. Med. Image Anal. 2018, 49, 1–13. ↩︎ ↩︎ ↩︎

3. Xun Huang, Ming-Y u Liu, Serge Belongie, and Jan Kautz. Multimodal unsupervised image-to-image translation. In Proceedings of the European conference on computer vision (ECCV), pages 172–189, 2018. ↩︎

4. Taesung Park, Alexei A Efros, Richard Zhang, and Jun-Yan Zhu. Contrastive learning for unpaired image-toimage translation. In European Conference on Computer Vision, pages 319–345. Springer, 2020. ↩︎

5. Chen Qin, Bibo Shi, Rui Liao, Tommaso Mansi, Daniel Rueckert, and Ali Kamen. Unsupervised deformable registration for multi-modal images via disentangled representations. In International Conference on Information Processing in Medical Imaging, pages 249–261. Springer, 2019. ↩︎

6. Moab Arar, Yiftach Ginger, Dov Danon, Amit H Bermano, and Daniel Cohen-Or. Unsupervised multi-modal image registration via geometry preserving image-to-image translation. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 13410–13419, 2020. ↩︎

7. Zhe Xu, Jie Luo, Jiangpeng Yan, Ritvik Pulya, Xiu Li, William Wells, and Jayender Jagadeesan. Adversarial uni-and multi-modal stream networks for multimodal image registration. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 222–232. Springer, 2020. ↩︎

8. Chengjia Wang, Guang Yang, Giorgos Papanastasiou, Sotirios A Tsaftaris, David E Newby, Calum Gray, Gillian Macnaught, and Tom J MacGillivray. Dicyc: Gan-based deformation invariant cross-domain information fusion for medical image synthesis. Information Fusion, 67:147–160, 2021. ↩︎

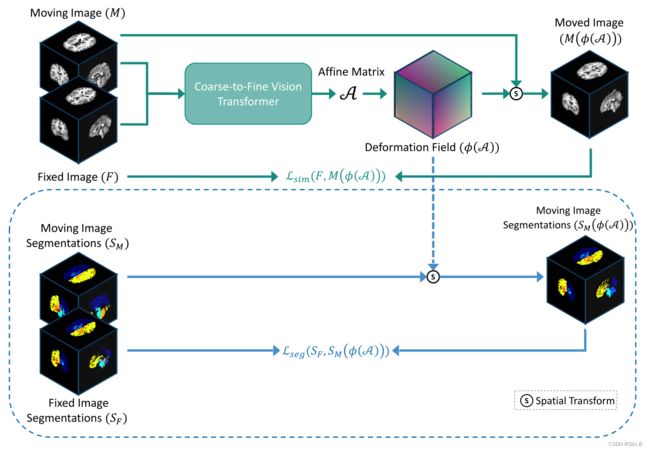
9. “Affine Medical Image Registration with Coarse-to-Fine Vision Transformer” (CVPR 2022), written by Tony C. W. Mok and Albert C. S. Chung. ↩︎

10. Blendowski, M.; Hansen, L.; Heinrich, M.P . Weakly-supervised learning of multi-modal features for regularised iterative descent in 3D image registration. Med. Image Anal. 2021, 67, 101822. ↩︎ ↩︎

11. Siebert, H.; Hansen, L.; Heinrich, M.P . Learning a Metric for Multimodal Medical Image Registration without Supervision Based on Cycle Constraints. Sensors 2022, 22, 1107. https://doi.org/ 10.3390/s22031107 ↩︎

12. Yan K, Cai J, Jin D, Miao S, Guo D, Harrison AP, Tang Y, Xiao J, Lu J, Lu L. SAM: Self-supervised Learning of Pixel-wise Anatomical Embeddings in Radiological Images. IEEE Trans Med Imaging. 2022 Apr 20;PP. doi: 10.1109/TMI.2022.3169003. ↩︎ ↩︎ ↩︎

13. F. Liu, K. Y an, A. P . Harrison, D. Guo, L. Lu, A. Y uille, L. Huang, G. Xie, J. Xiao, X. Y e, and D. Jin, “SAME: Deformable Image Registration based on Self-supervised Anatomical Embeddings,” in MICCAI, 2021. ↩︎