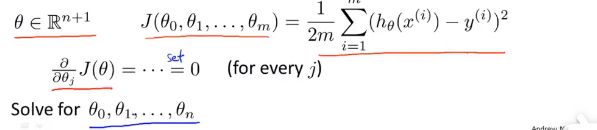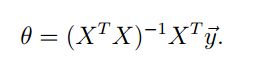吴恩达机器学习视频学习笔记

学习并实践它们！老师你好！欢迎来到我的blog。

• （21.8.4更新）在差不多快要学习玩吴恩达的深度学习和神经网络课程之后，回过头来看这篇关于吴恩达机器学习课程的学习笔记，发现自己不论是在记笔记的方式或者记录学习内容方面还有待加强，比如：使用过多的课程ppt截图，但是截图的质量和画质不高；还有记录过程中缺少自己独特的、深入的思考。所以今后会陆陆续续对这篇文章进行改进，一方面在学习了深度学习之后回过头来加深对整个机器学习领域一些算法的理解；另一方面我会这里增加一些新学习的机器学习知识，如决策树一类的。到时候似乎得改标题了:)

介绍 Introduction

机器学习的定义
    机器学习一直没有一个统一的定义，一种经常引用的英文定义来自Tom Mitchell的《机器学习一书》：A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its’performance at tasks in T, as measured by P, imporves with experience. 其对应的中文译文：如果用P来衡量计算机程序在任务T上的性能，根据经验E在任务T上获得性能改善，那么我们称该程序从经验E中学习。

如何学习机器学习
    如何学习机器学习或者说机器学习的路线是什么？这是一个需要机器学习初学者弄懂的问题。
    从学习背景来说，机器学习需要必要的数学知识（微积分，线性代数，概率论与统计学，优化理论等）和关于一些用于科学计算的编程语言（如Matlab ，Octave，Python，R等）。

监督学习和无监督学习
    可以根据是否有label来区分监督学习和无监督学习。监督学习主要包括分类和回归两种形式，无监督学习主要包括聚类和关联分析。
    在本blog中涵盖的监督学习算法有：线性回归、logistic regression、神经网络、支持向量机(SVM)、协同过滤，涵盖的无监督学习算法有：K-Means、主成分分析(PCA)

线性回归 Linear Regression

单变量 One Variable

梯度下降算法 “Batch” Gradient Descent Algorithm
    梯度¹下降法,就是负梯度方向来决定每次迭代的新的搜索方向,使得每次迭代能使待优化的目标函数逐步减小。用于求函数的局部最小值，它遍历了所有样本点，而有些算法只关注小集合内的样本点。

例子：房价预测
从最简单的单变量线性回归开始，假设函数h_θ(x) =θ₀+θ₁*x；θ₀，θ₁为模型参数，问题是如何选择模型参数，使得代价函数²最小。

梯度下降算法如下图所示：（其中α³是学习速率）

这里有几个问题需要注意：
    1、需要同时更新参数模型，吴恩达老师没有解释。
    2、梯度下降算法可能获得局部最优解。但是线性回归的梯度下降的代价函数是一个下凸函数，它没有局部最优解，只有全局最优解。
    3、学习速率太小导致下降梯度太小；学习速率太大可能导致无法收敛或者发散。
    4、随着我们越来越靠近局部最优解，导数值/偏导数值越来越小，梯度下降法每一步的幅度自动地越来越小。

多变量 Multiple Variables

多元梯度下降算法
    随后讨论的是多变量线性回归，多变量线性回归是指自变量有多个的线性回归问题。此时模型参数->模型参数向量。

算法如下：

单元梯度下降算法和多元梯度下降算法对比：

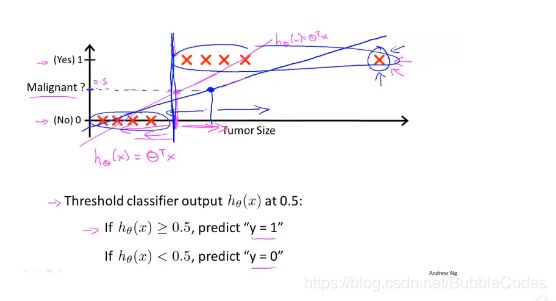
根据J-Iteration曲线判断收敛性：
    学习速率α不同，代价函数的收敛情况和收敛速率都有可能发生改变。
    当该函数图像是发散的时候，我们需要适当调小α，当收敛速度过慢时，可以适当调大α。

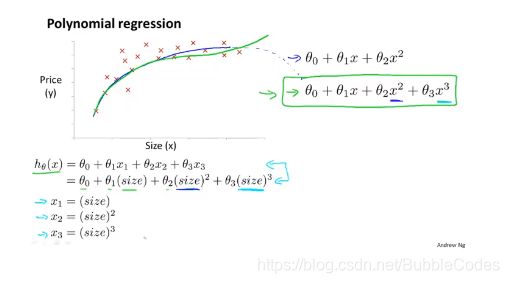
多项式回归 Polynomial Regression

    多项式回归是线性回归的一种，在一般形式的多项式回归中，特征向量中的某些维是多次项，合理选择多项式的特征向量可以使预测函数图像曲线和样本拟合地更好。上述的线性回归其实是多项式回归的一种特殊情况。

正规方程 Normal equation

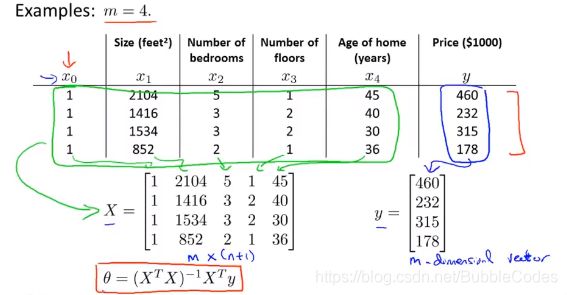
    正规方程是一种求解最小化代价函数J(θ)参数θ的方法，其区别于上述梯度下降中迭代的思想，正规方程通过数学解析的方法直接求出代价函数最小值。
并且不需要特征缩放。
    其中的数学思想是：由于代价函数为凸函数，所以求解偏导数为0的点，该点即为最小值点。

    关于θ向量的代价函数如何求最小值：

    求解出来θ值为：

    例子：

梯度下降法和正规方程对比：
    主要在于当n十分大时，选用梯度下降法，n不大时使用正规方程法。

线性回归运用时可能出现问题
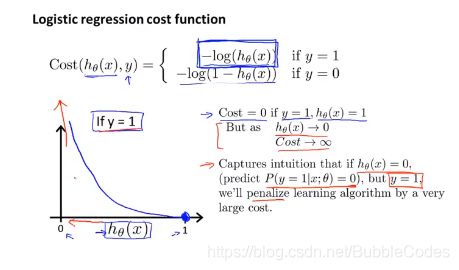
    例子：判断肿瘤的良性与恶性，如果套用线性回归，则会出现一下问题：
    当出现某些偏离一般位置的点时，对预测结果影响较大。

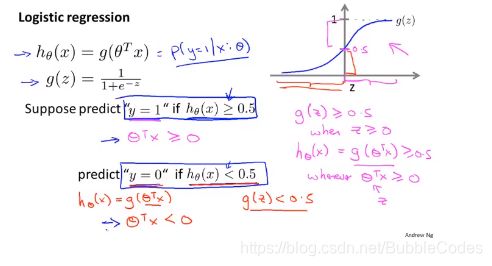
Logistic Regression

    Logistic Regression里面含有回归regression，但它其实是分类算法，而不是回归算法。
    分类算法和回归算法在本质上是一样的，分类算法主要解决的问题是：给我数据，我将该数据归类为某一类，其预测值为离散值，而回归算法预测值为连续值。例如预测明天温度30℃以上还是一下和具体多少度。

单分类(OCC) One-Class Classification

    决策边界⁴不是数据集的属性，而是假设本身的及其参数的属性。即决策边界是假设函数的一个属性，有确定的参数值（θ向量）我们就可以直接得到决策边界。数据集->预测函数->决策边界

如何获得logistic regression的参数θ向量？

    由于预测函数h_θ(x)为复杂的非线性函数，所以代价函数J(θ)不一定是凸函数convex。如果使用梯度下降法，那么可能不会收敛到全局最优解处。
    基本思想是修改代价函数为凸函数，但是代价函数所代表的意思不变，然后仍然使用梯度下降算法来解决问题。
    故解决方案为：我们可以修改cost function使得其为凸函数convex function

    先定义cost函数以下形式：
    y=1时，h_θ(X)趋向于1，代价J越小，最小值为0，最大值为无穷大；反之y=0时，h_θ(X)趋向于0，代价越小，最小值为0，最大值为无穷大。
    由此将非凸函数优化问题重新修正为凸函数优化问题，即解决了局部最优解问题。

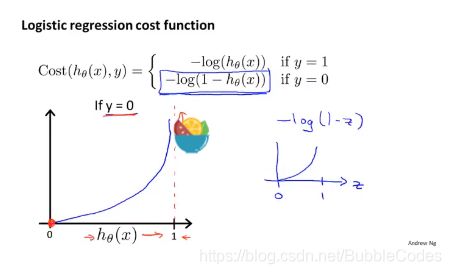
    得到cost函数后，将cost函数的分段形式变成统一的形式，并得到代价函数J(θ)。将表达式合并的方法有很多，这里来自于统计学中极大似然法。

将预测函数的值域压缩到[0,1]，此时预测函数表达为预测为某分类值得概率。

logistics regression代价函数求导：
$$\begin{gathered} \frac{\partial L}{\partial w}=\frac{\partial L}{\partial \hat{y}}\ast \frac{\partial \hat{y}}{\partial \hat{z}}\ast \frac{\partial z}{\partial w} \\ \frac{\partial L}{\partial w}=-\frac{1}{m}\Sigma \{[y\ast \frac{1}{\hat{y}}+(1-y)\ast \frac{1}{1-\hat{y}}]\ast \hat{y}\ast (1-\hat{y})\ast x\} \\ \frac{\partial L}{\partial w}=\frac{1}{n}\Sigma [(\hat{y}-y)\ast x] \end{gathered}$$
    此时我们惊讶地发现，代价函数对模型参数θ得偏导与前面linear regression表达式相同。那么难道说线性回归和logistic regression相同吗？
    答：不同，表达式看似相同，其实假设预测函数得表达式以及不同。

    optimization algorithm：
    1、gradient descent
    2、conjugate gradient
    3、BFGS
    4、L-BFGS
    线搜索算法

多分类问题 Multi Classification

    多分类问题解决得思想是：One VS. All，即对于每一类都做一个分类器，用于分出该类和其他类，这样对于某数据集进行多分类预测时，即将每一数据都带入所有分类器中，哪个分类器的预测概率越大，则预测为哪一类。

正则化 Regularization

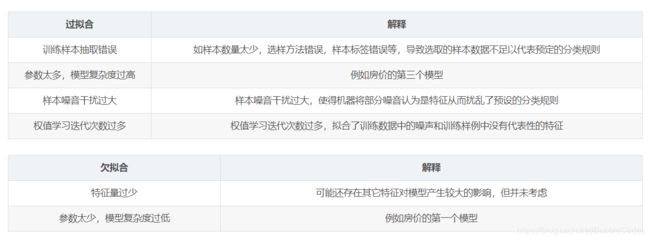
过拟合 Overfitting 和 欠拟合 Underfitting

    回归问题和分类问题都有可能出现过拟合的现象，在回归问题中过拟合情况为：拟合曲线过于复杂；在分类问题中过拟合情况为：决策边界过于复杂。


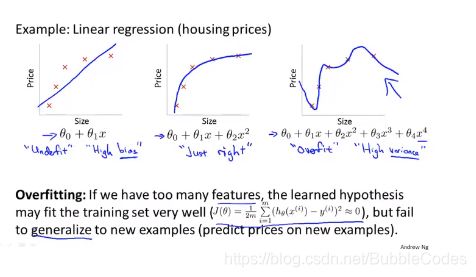
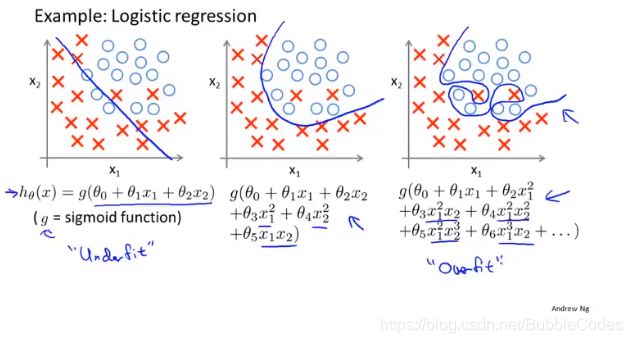
    过拟合在数学上体现为高方差（high variance），具体表现为曲线过于复杂，泛化能力⁵不强。
    欠拟合在数学上体现为高偏差（high bias），具体体现为曲线过于简单，对数据的拟合能力不强。

引起过拟合和欠拟和的原因

    缓解过拟合问题overfitting的选择：
    1、手动或者使用模型选择算法来舍弃一些特征。但是可能所有的特征都是有用的。
    2、正则化regularization：保留所有的特征，但是降低特征变量的量级。

    环节欠拟和问题underfitting的选择：
    1、增加数据量
    2、增加特征向量的维度，提高模型复杂度

正则化解决过拟合 Overfitting

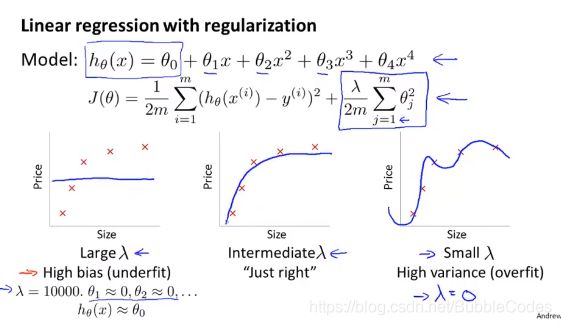
    正则化的思想是：在不减少特征向量的维度的前提下，通过在代价函数J(θ)中添加正则项的，从而对特征向量的每一维对应的参数进行“惩罚 penalizing”（效果是xx前面的系数变小），最终达到缓解过拟合的效果。
    其中：λ为参数类似于学习速率α，λ越大，惩罚越大；λ越小，惩罚越小。

    惩罚机制penalizing例子：
    在下图中添加了正则项，为了是代价函数达到最小，θ₃和θ₄会变得很小，从而x₃和x₄前面的系数很小，从而简化了模型。

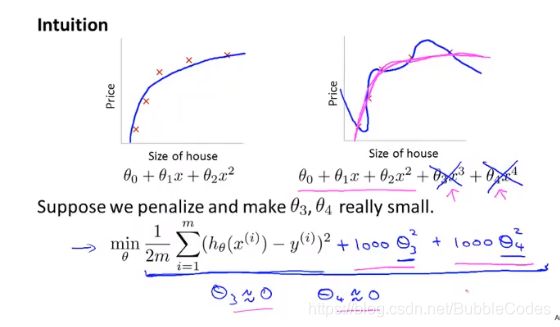
    λ起了平衡我们两个目标的作用：更好地拟合和保持特征值小。 但是如果λ太大，则惩罚penalizing太大，那么可能导致欠拟合，如下图所示。

    一般我们不penalizing惩罚θ_0，为什么？
    我的看法：theta_0对应的特征值为x_0，而x_0恒为1，故θ_0项只影响h函数的截距，对过拟合和欠拟合问题没有影响。
而由于cost function中正则化项不包括theta_0，所以grad J自然也不包括theta_0。

    并且正则化一般在特征向量维数较高，而数据集较小时使用，因为此时易出现overfitting。

正则化线性回归
    线性回归求解参数向量θ两种方法：梯度下降算法和正规方程算法
    梯度下降算法修改（添加正则项）：

    正规方程法修改：

    optional/advanced：在使用正则方程时，可能会出现矩阵不可逆的情况，而在使用了正则化regularization之后矩阵变得可逆，解决了这一问题。

神经网络 Neural Network

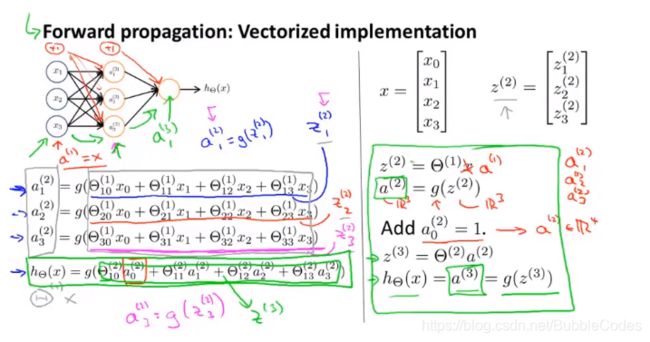
前向传播算法 Forward Propagation Algorithm

    在有了线性回归和logistic regression之后为什么我们还需要Neural NetWork呢？
    原因如下：
    我们之前学的，无论是线性回归还是逻辑回归都有这样一个缺点，即：当特征太多时，计算的负荷会非常大.

    假使我们采用的都是 50x50 像素的小图片，并且我们将所有的像素视为特征，则会有2500 个特征，如果我们要进一步将两两特征组合构成一个多项式模型，则会有约25002/2个（接近 3 百万个）特征。普通的逻辑回归模型，不能有效地处理这么多的特征，这时候我们需要神经网络。所以Neural Network可运用于计算机视觉。

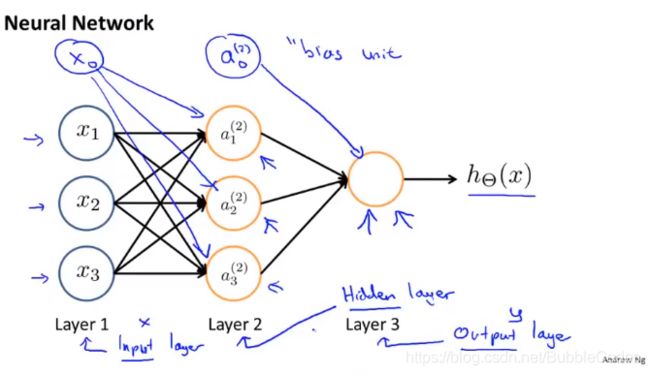
    Nerual Network的基本结构如下图所示：
    Nerual Network主要包括输入层⁶Input Layer、隐藏层⁷Hidden Layer和输出层⁸Output Layer，其中每层都有一个独立于其他神经元的偏置单元⁹Bias Unit，从前一层到后一层的单向全连接表示数据的流动和处理过程。每个层到后一层的权重参数θ构成的矩阵称为权重矩阵¹⁰但直接通过前一层和权重矩阵只能直接得到Z向量，Z向量到A向量还要通过激活函数¹¹（sigmoid函数）的映射得到。

    Nerual Network向量表示形式：

    神经网络有个很大的特点是：它不直接使用已有的特征，而是通过学习获得新的更复杂的特征，这些特征往往难以理解。
    神经网络中神经元的连接方式成为神经网络的架构，不同的连接方式就是不同的架构。

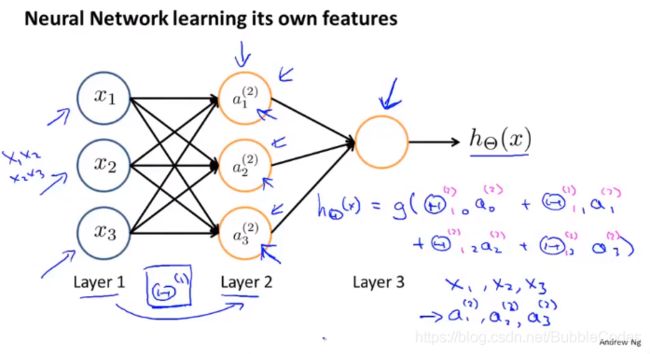
用neural network的简单例子：
    AND运算：

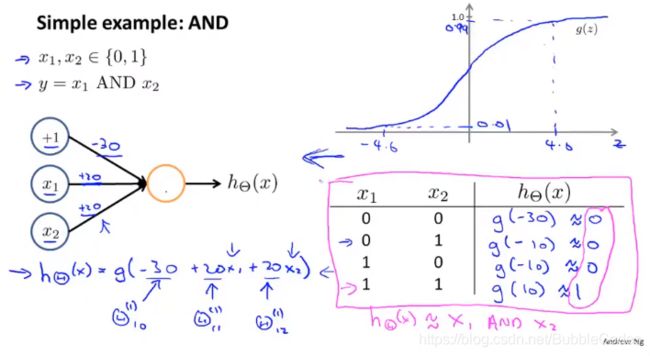
    OR运算：

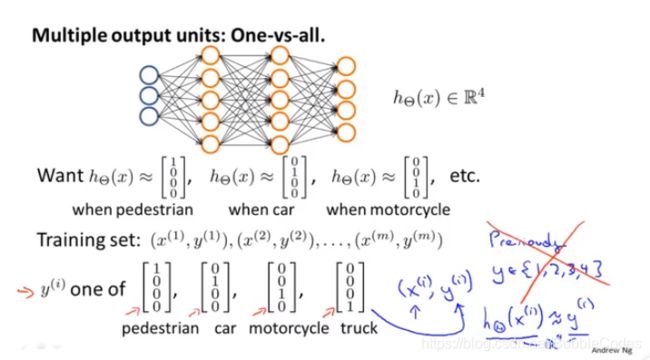
Neural Network神经网络 解决 多分类问题Multi-Class Classification
    例子：数字识别
    数字识别实际上就是多分类问题。其采用的方法本质上是一对多法One VS. All的拓展，在神经网络的架构上就是增加输出层，在每一次预测中我们取输出层中输出最大的一类作为预测结果。

Neural Network的CostFunction代价函数
    神经网络中的代价函数J(θ)是综合了所有分类器的代价函数，以相加的形式将他们连接起来。

反向传播算法(BP) Back Propagation Algorithm

    反向传播算法的基本思想是：从输出层开始，逐层向前计算误差δ。

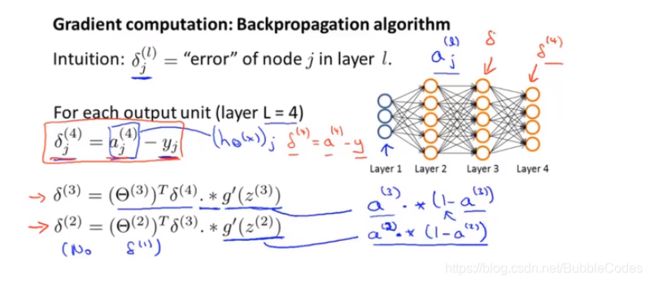
    Back Propagation Algorithm 框图：

梯度检验 Gradient Checking

    梯度检验的基本思想是利用数学上的导数/偏导数的定义的思想，在2*ε很小的情况下，将两点连线的斜率近似等于中点的曲线斜率，由此验证在算法中计算得到的导数/偏导的准确性。

    在θ为实数的情况下，计算过程如下图：

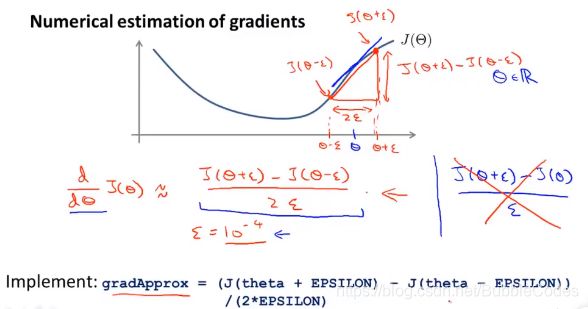
    θ是向量的情况下，计算过程如下图：


总结
    检验得知你的误差前向传播算法准确之后，关掉梯度检验算法，因为它计算量太大。

随机初始化Random Initialization

    在之前的θ向量初始化采取的策略是：zero initializtion(对称权重问题problem of symmetric weights)，这样初始化会出现同层hidden unit完全对称，出现高冗余，权重都相同。
    所以在这里我们采取随机初始化的策略。

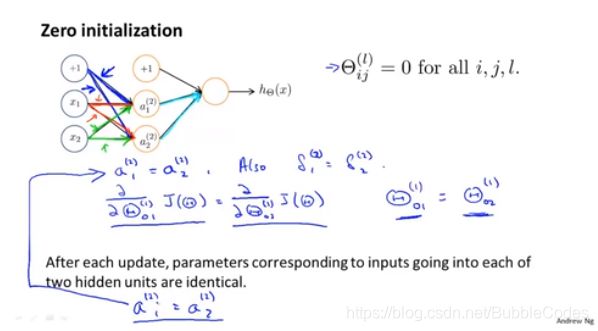
random initialization
    对于权重矩阵中的每一个θ，我们选用[-ε, ε]的均匀分布来初始化它。

neural network 总结
    1、选择网络架构network architecture：connectivity pattern between the neurons。输入层和输出层units由特征维度和分类个数决定。注意输出矩阵y需要recoded as [1 0 0 …]T

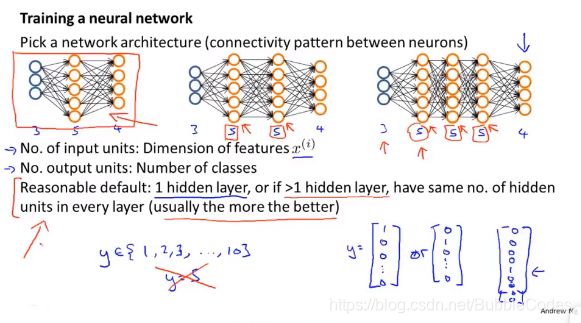
    2、训练一个神经网络的基本步骤training a neural network
    初始化权重矩阵initialization weights
    前向传播算法计算预测值forward propagation
    获得代价函数get J(θ)
    反向传播算法计算误差矩阵backpropagation to get dJ/dθ
    梯度检验gradient check
    gradient descent or other advanced optimization methods to minize J(θ)(nn cost function is non-convex,it can 收敛到局部最优解而不是全局最优解)

Advice for Applying Machine Learning

Debugging a learning algorithm

手段method
    当算法出现问题时，你能够实施的手段有哪些？
    1、更多的数据集
    2、更多/少的特征
    3、添加多项式特征
    4、减小/增大惩罚系数λ

评估estimate 机器学习算法性能指标
    误差bias小并不一定说明他是一个好的假设方程，它还有可能是过拟合overfitting了。

判断over fitting的手段：
    1、观察拟合图像（用处不大）
    2、将样本分为training set、cross validation set、test set，分割比例一般6:2:2

    在训练集、测试集后，利用训练集训练的模型（参数θ向量）分别计算训练集的代价J_train(θ)、验证集的代价J_cv(θ)、测试集的代价J_test(θ)

    计算泛化误差的基本步骤：
    1、最小化每个模型的训练误差，获得training error最小的模型(Theta向量)。
    2、计算每个模型的cross validation error（交叉验证误差），选择交叉验证误差最小的模型。（但是不用它作为泛化误差）
    3、使用test set计算选择模型的test error，将其作为泛化误差。

机器学习诊断法 Machine Learning Diagnostics
    （variance）overfit：训练误差很小，泛化误差很大。
    （bias）underfit：训练误差和泛化误差都很大，大小相近。

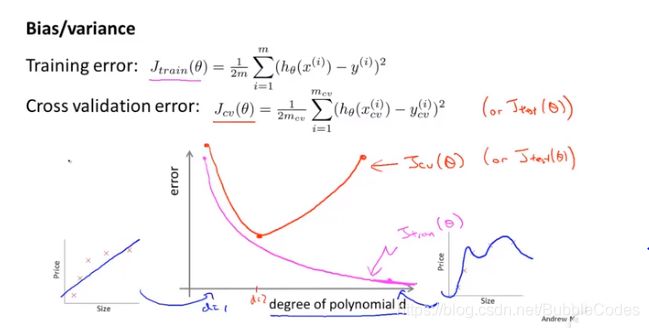
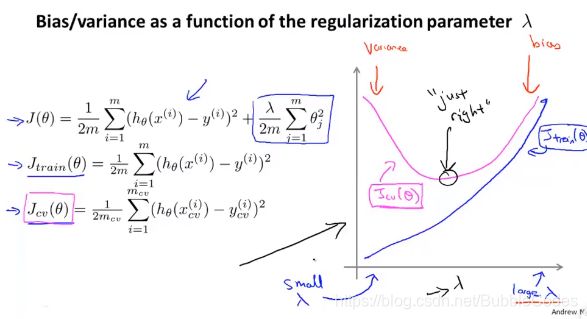
正则化Regularization 和 误差、方差
    λ过大时，惩罚过大，导致underfitting，bias过大；
    λ太小时，惩罚过小，导致overfitting，variance过大；

选择lambda(regularization)
    1、生成λ序列，使用序列中每一个值最小化cost function得到对应的θ矩阵。
    2、计算每个θ的交叉验证损失，找出最小的交叉验证损失对应的λ和θ，并选择测试损失作为模型的泛化能力的指标。

    误差/方差与lambda关系图：

Learning Curves

    用途：检查算法准确性或者优化算法，诊断是否存在bias problem or variance problem
    变化训练集training set的size，观察training cost和交叉验证误差。

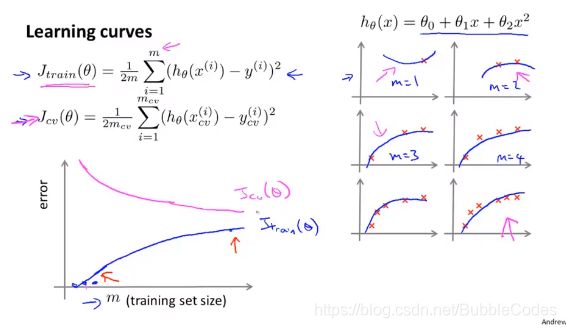
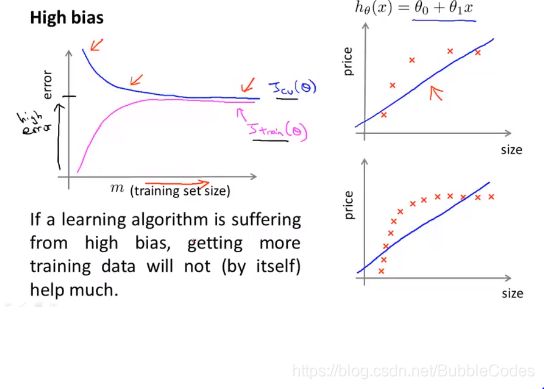
high bias高误差情况下
    在高误差情况下，训练误差和交叉验证误差最后差不多重合,给予足够多的training set量也不能降低test cost和cross validation误差。
    个人理解：因为模型过于简单，盲目提高训练集的大小并不能有效降低两个误差，此时是模型的假设限制。

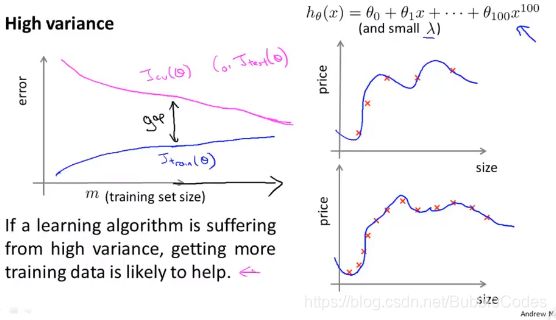
high variance高方差情况下
    给予更多的训练集有助于降低cross validation cost和test cost。

如何选择方法去优化算法
    more training -> fix high variance
    less features -> fix high variance
    more features -> fix high bias
    increase λ -> fix high variance
    decrease λ -> fix high bias
    总体的思路时，一开始尽量将模型的复杂度提升到足够高，当发现出现overfitting问题时，在考虑用正则化或者其他解决方案解决过拟合。

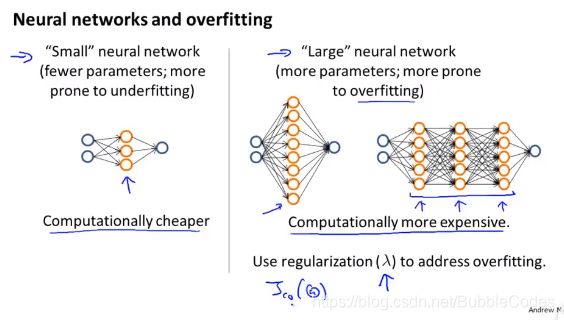
nerual network 和 overfitting
    如何选择神经网络的结构（连接结构）？总的来说：
    1、在满足精确度的前提下使hidden layer少，神经元单位少的神经网络（简单的神经网络）计算量少，但是可能存在underfitting
    2、对于复杂的神经网络，计算量较大，可能出现overfitting。
    3、选择的原则是：通常选择更复杂的神经网络，并且再出现overfitting时，使用regularization（正则化）解决overfitting的问题。
    4、对于hidden layer的层数选择，可以从小到大以此计算cross validation cost，选择小的那个。

机器学习系统设计 Machine Learning System Design

确定工作的重心 Prioritizing What to Work On

    例子：垃圾邮件分类问题

设计流程
    在设计一个机器学习系统时，推荐的方法是：
    1、快速实现一个简单的算法，测试其cross validation cost。
    2、画出learning curves，判断其是否存在bias或variance问题，在那之后在判断是什么方法来解决。（避免过早优化）
    3、进行错误分析

误差度量 Error Metric

    通常在实现完一个简单的算法之后，我们需要判断加入某些细节能否提升我们算法的性能，比如：构建更复杂的特征等，此时我们需要一个关于算法好坏的度量。从该误差度量上，我们可以清楚地知道算法的性能是否提升。
    一般，我们选择例如准确率的量来评估算法的性能，比如：在癌症诊断中分类出的人中的真正癌症患者占所有人的比例等等。

不对称性分类的误差评估
    有时单纯只考虑一种情况的指标是不能很好地作为算法性能的指标的，例如例如我们希望用算法来预测癌症是否是恶性的，在我们的训练集中，只有 0.5%的实例是恶性肿瘤。假设我们编写一个非学习而来的算法，在所有情况下都预测肿瘤是良性的，那么误差只有 0.5%。然而我们通过训练而得到的神经网络算法却有 1%的误差。这时，误差的大小是不能视为评判算法效果的依据的。
    skewed classes 偏斜类的问题：正样本的数量比负样本的数量多得多。当出现偏斜问题时，使用分类精度来衡量（error rate or accuracy rate）算法并不是一个好方法。

precision/recall查准率和查全率
    查准率precision表示准确率，即正确预测为1占所有预测的数目的比例；查全率recall表示没有漏掉的程度，即预测为1占所有实际为1的比例。
    只有precision 和 recall都高的模型才是好模型，在某些特定情况下，漏判和误判严重程度不同，所以有时更侧重与某一种。

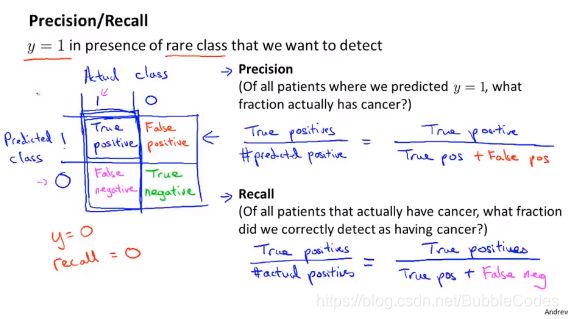
precision和recall的权衡
    如果我们希望提高查全率，尽可能地让所有有可能是恶性肿瘤的病人都得到进一步地检查、诊断，我们可以使用比 0.5 更小的阀值，如 0.3。我们可以将不同阀值情况下，查全率与查准率的关系绘制成图表，曲线的形状根据数

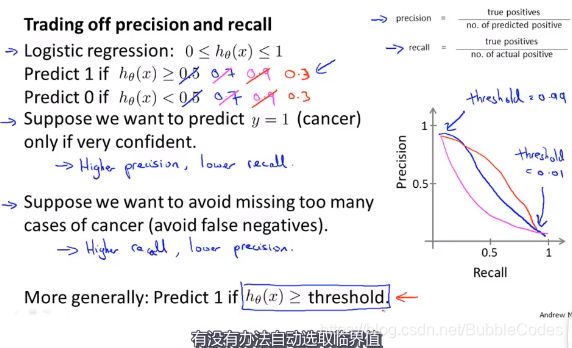
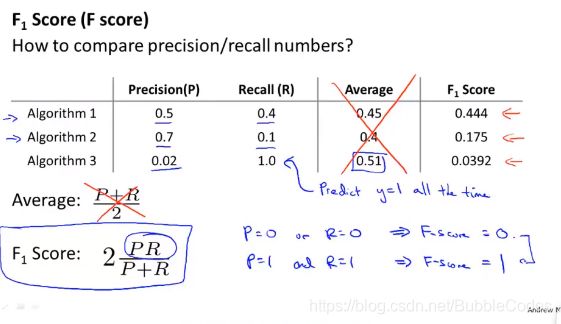
调和平均数F₁Score
    我们选择调和平均数来均衡准确率和查全率：调和平均数。调和平均数的趋势是使二者的值尽量相等，体现我们对于需要二者同时高的需求。

支持向量机 (SVM) Support Vector Machines

从Logistic Regression 到 SVM

    考虑costfunction中，当y = 1时，画出costfunction图像，如左下角所示，在SVM中与logistics regression中不同的是，我们使用洋红色的折现代替曲线。同理对于y = 0时，我们做相同的近似。

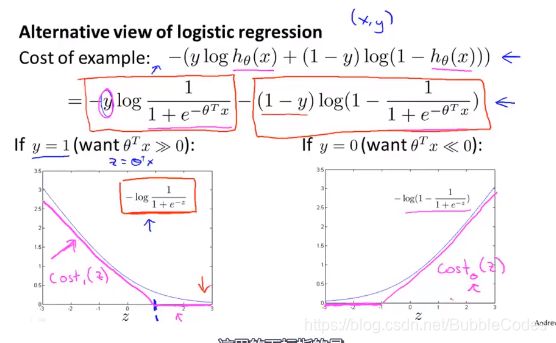
    在替换成cost₁和cost₂之后，将1/m常数去掉，不影响costfunction，将regularization term中的λ等价为A项前面的系数C（λ用来作为惩罚项的系数，使用C作为前项的系数可以做到同样的效果C不一定对于1/λ）

    最后与logistics regression不同的是，在最小化cost function之后得到的参数theta，计算预测值h(x)方法不同，在前面都是把其作为概率看待，而这里直接作为预测值。

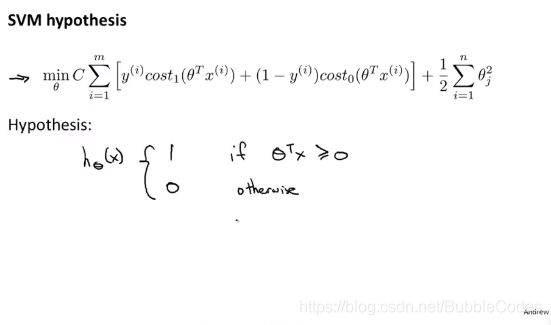
大间距分类器 Large Margin Classifier

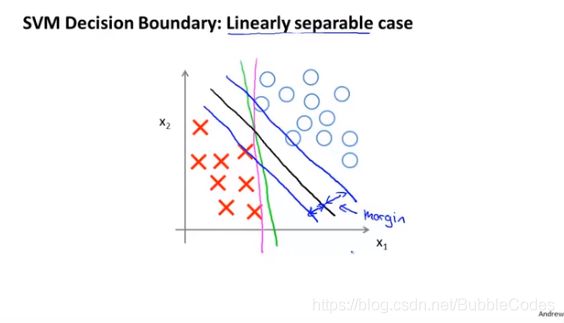
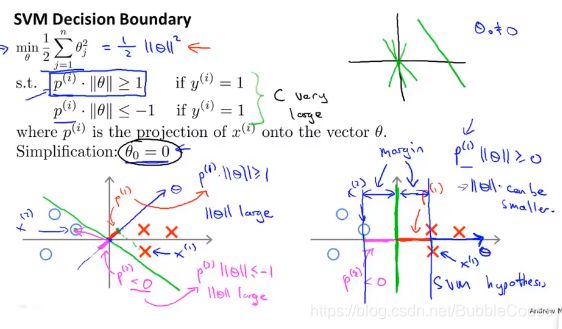
    在修改后的cost function中，如果C较大时，如果想使得cost function最小，我们需要当thetaX≥1或者thetaX≤-1，此时我们的分界线不再是0，而是1和-1。这使得其有一定的robust（鲁棒性），而不是恰好将二者分开。

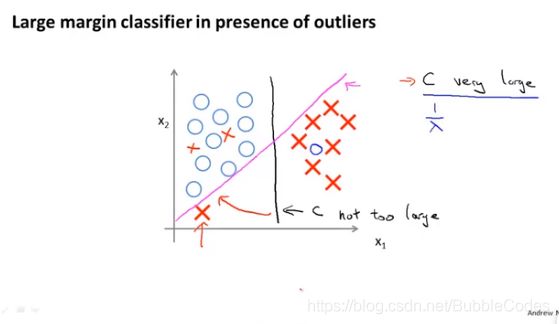
    当C非常大时，模型就像是急切地想将二者全部分开，而使得margin变小，决策边界变为洋红色。当C不是太大时，决策边界变为黑色。

大间隔分类器large margin classifier的数学原理

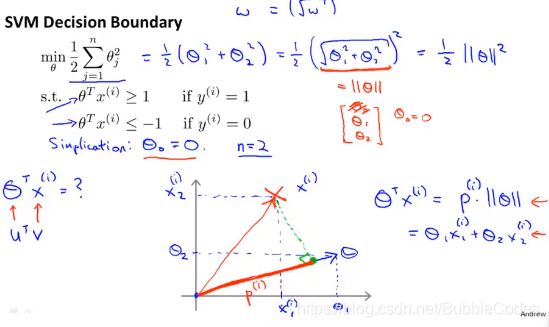
    由于我们的优化目标等价于最小化θ，故若使Pi*theta≥1或者≤-1，则Pi要尽量大，即每个数据点到决策边界的距离要尽量大。所以将SVM又称为大间隔分类器。
    有一个要注意的点：在计算cost function中用的是1和-1作为分界线，而在h函数中判别时用的是0作为分界线。

核 kernel

    我们将特征向量X替换为特征向量f。为什么这样做？

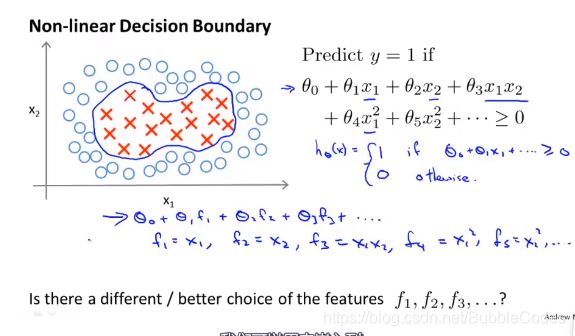
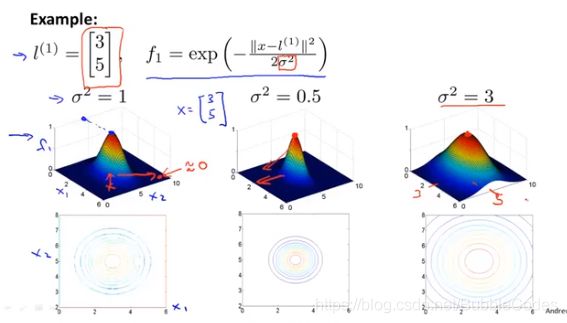
    similarity为相似函数，表示x样本店与选取的l点的相似程度，即：两点靠的越近相似程度越高，其也称为核函数。而后面的exp项只是为高斯核函数，是核函数的一种。
    理解：每一个点是一个核，与核靠的越近，获得的参数越靠近1；而与某个核越远，获得的参数越靠近0；
    在做完特征向量的转变之后，特征向量的维度发生了改变，从n->m。fi代表m个样本点在第i维空间内的值。


高斯核函数为例：


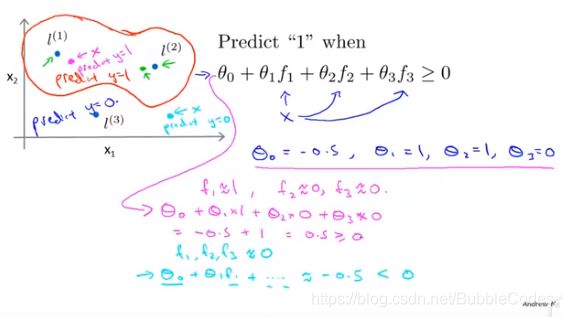
    如何得到核?
    直接将training set中的每一个样本点作为标记点

    带核函数的SVM训练预测的基本过程：
    已知样本输入和输出，利用kernel核函数得到每一个样本对应的特征向量xi作为新的特征向量，并以此最小化cost function。获得参数向量theta。

    关于是否可以将核函数的思想应用于logistic regression的问题，吴恩达教授这样说：如果你硬是要这样做也不是不可以，但是那些专门用于带核函数的支持向量机SVM的运算技巧可能不能很好的泛化到logistic regression。所以运算时长增长。
    此外吴恩达教授还补充了关于如何选择支持向量机的参数：（偏差-方差折衷bias-variance trade off）
    参数C的作用与1/λ相同。即C大时，λ小，对应低偏差、高方差的模型。
    参数σ²是高斯核函数中的参数。当σ偏大时，模型有高偏差和低方差。当σ偏小时，有低偏差和高方差。原因分析如下（？）：
    当σ偏大时，高斯核函数的分布较为扁平光滑，表示即时与标记点相差较远时，参数的值

解决SVM中的问题
    一般来说调用库帮助我们解决大部分的问题，但是这里仍然有些需要注意的地方：
    1、参数C的选取
    2、kernel核函数（相似函数）的选择

例子：
    线性核函数linear kernel即是不使用核函数，即特征向量没变。 当特征向量维度十分高，而样本数量十分少时，我们也许只需要拟合一个简单的决策边界，而不是一个非常复杂的非线性决策边界，因为没有足够的数据，我们的边界可能会overfitting。

    如果你已经选择高斯核函数，那么：
    在一些SVM包中，它们可能需要用户提供kernel核函数。在使用高斯核函数之前，你也可能需要做特征缩放

    使用核函数的目的是什么？为什么要进行特征向量的变维？和聚类有关系吗？
    答：在使用kernel时需要注意的是，许多关于求θ的算法都只适用于满足mercer’s theorem的核函数，通常我们使用高斯核函数和线性核函数最多。

关于SVM用于多分类问题时
    其基本思想即时之前学习过的one vs all，即KSVMS，训练K个分类器。

关于面对分类问题如何选择logistic regression还是SVM
    当n≥m是，一般使用logisticregression 或者线性SVM
    当n不大，而m较大时，一般使用高斯核函数SVM
    当n不大，而m很大时，通常我们手动增加特征向量维度，然后使用logistic regression，因为此时使用高斯核函数SVM耗费时间太长。
    有时面对一些问题时，我们一般不使用neural network，因为耗费时间太长。

    SVM是凸优化问题，所以不需要考虑局部最优解的问题。而neural network的这个问题不大不小。

聚类 Clustering

    与监督学习最大的区别是：unsupervised learning的数据集没有标签，没有y。

K-Means算法

    cluster centroid聚类中心
    K-Means算法步骤：
    1、随即地选择一些聚类中心，要多少簇就做多少个聚类中心。
    2、内循环一：寻找每一个样本点最近的聚类中心，从而将样本点分为K类
    3、内循环二：计算每一类样本的均值点，随之将相应的聚类中心更新为均值点
    4、循环2、3操作

    问题：如果某些聚类中心没有分到样本点，则通常的做法是：去除这个聚类中心。还有一种做法：去掉这样聚类中心之后，再随机一些样本中心。

K-Means 优化目标函数
    作用：帮助我们调试算法，帮助我们寻找更好的簇并且避免局部最优解。

    带着失真函数distortion思考K-Means算法：
    1、内循环一实质上是通过分类样本（C）来最小化J
    2、内循环二实质上是通过移动centroid聚类中心（μ）来最小化J

初始化聚类中心
    聚类中心数目K一般小于样本数m：K＜m；随机初始化聚类中心可能使得K-Means算法落到局部最优解。
    为了得到一个尽可能好的局部最优解或者全局最优解，可以尝试的做法是：多次随机初始化聚类中心μ

随机初始化算法：
    将之前的K-Means算法执行50-1000次，从中寻找畸变函数distortion function最小的情况。
    一般来说我们只在k=2-10的情况下使用这样的方法，因为当K相当大时，这样的作法对于局部最优解问题改善不大。

如何选择聚类数量K
    由于这是无监督学习，因而没有准确的答案。

    1、肘部法则elbow method
    左边情况有明显转折点，易于做出选择。
    右边情况没有明显转折点，肘部法则失效

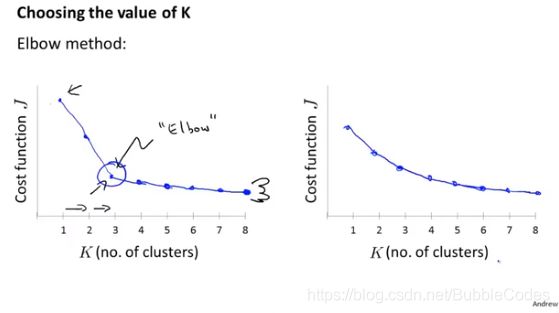
    2、另一种方法是结合实际，你需要实际你需要多少就分多少。

降维 Dimensionality Reduction

动机：Data Compression 数据压缩
    样本中的特征可能是有冗余的，比如：两个特征一个以cm为单位，一个以inch为单位。
    数据压缩的好处：降低所需存储空间使机器学习算法运行更快

    例子：2D->1D，使用某种映射方法将所有样本的二位特征向量映射到一个一维特征向量

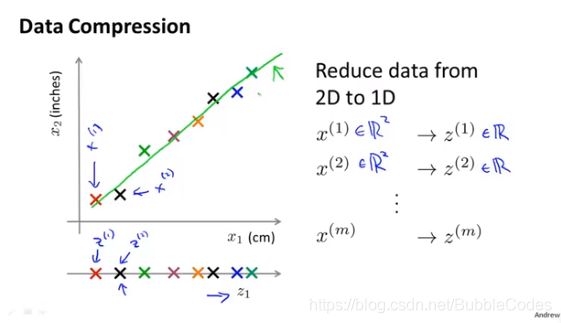
    例子：3D->2D
    三维空间的点大部分分布在一个二维平面周围，所有将所有的样本点投影到该平面内，并用新的特征值作为新的特征向量的两个维度。

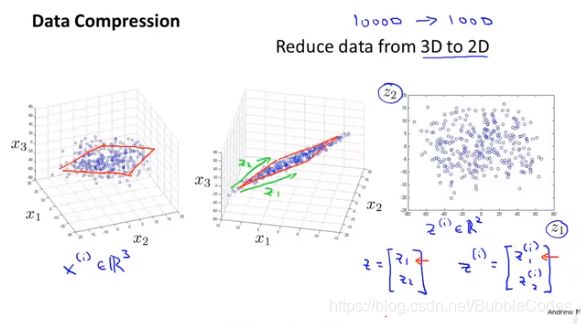
动机：可视化
    通过将高维的特征向量降维到3D或者2D，我们可以得到可视乎的图像，并分析图像中每一维可能代表的意义。

主成分分析(PCA) Principal Component Analysis

概念描述
    如果我们需要将ND的样本降维到KD，我们需要做的是：寻找K个向量使得ND样本在这K个向量组成的K维空间中的投影的projection error投影误差projection error最小。

    和线性回归的区别：
    1、linear regression做的是做预测，找出theta向量使得cost function最小，是拟合y和x组成的样本。
    2、principle component analysis(PCA)属于无监督学习，没有label y，我们需要找出k个线性无关的向量组成k维空间使得其在该空间内的投影最小。
简单点来说：linear regression只想最小化某个样本点（x1，x2…）的预测值和真实值的距离，而PCA想最小化样本点到投影之间的距离。

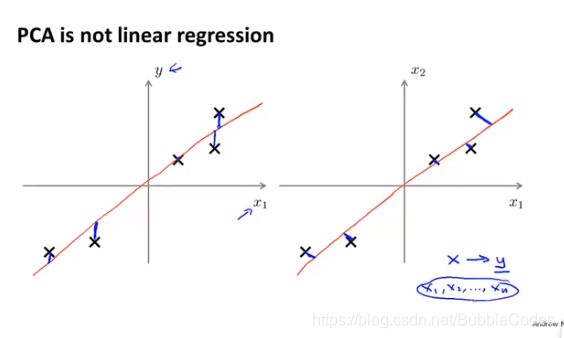
主成分分析算法 principle component analysis algorithm

特征向量eigenvector
奇异值分解 svd singular value decomposition
正定矩阵 symmetric positive

    先使用m个样本的特征向量计算协方差矩阵¹² (n*n)，随后调用奇异值分解（特征向量）函数得出特征向量矩阵 n * n（U），根据我们的需要（例如k个特征向量）从中提取前k个向量组成U_reduce，然后计算新的k维特征向量z。
    为什么取前k呢？因为我们需要将n维空间映射到k维空间且保证丢失的特征最少。

主成分数量选择


特征缩放¹³和均值归一化 feature scaling and mean normalization
    数据预处理一般步骤：减去均值使新均值为0，除标准差或者最大最小值之差进行特征缩放。

应用PCA的建议
    当监督学习算法由于存在过量的冗余特征而使得算法运行时间太长时，使用PCA适当减少特征向量的维度可以加速监督算法。

    PCA存在一些误用的情况：
    1、缓解过拟合
    2、第一时间将PCA考虑到算法设计中

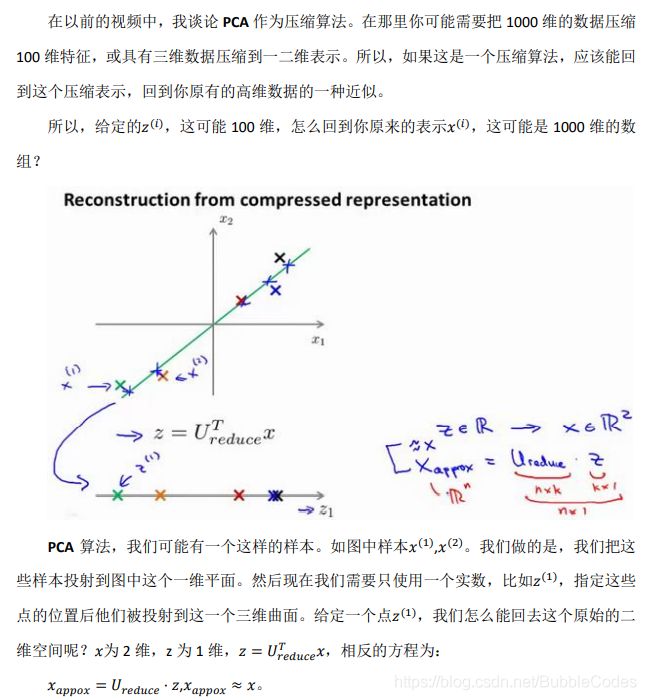
压缩重现 Reconstruction of the Driginal Data

异常检测 Anomaly Detection

高斯/正态分布 Gaussian/Normal distribution 和参数估计
    其中的主要问题是参数估计¹⁴问题：我们这里使用的极大似然估计。

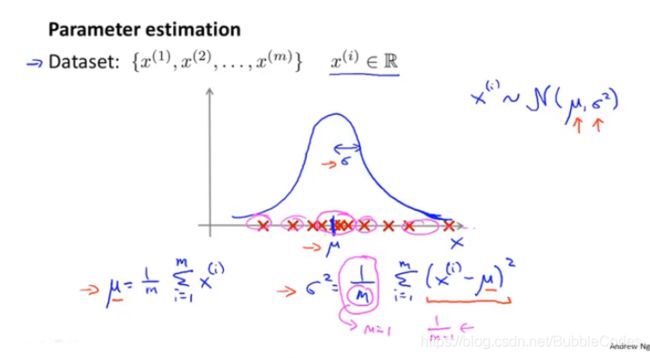
异常检测主要思想：
    对训练集X进行概率建模，得到其概率分布，并设置阈值ε，在随后给定一个新样本点时，计算概率密度函数在该点值（密度估计）。

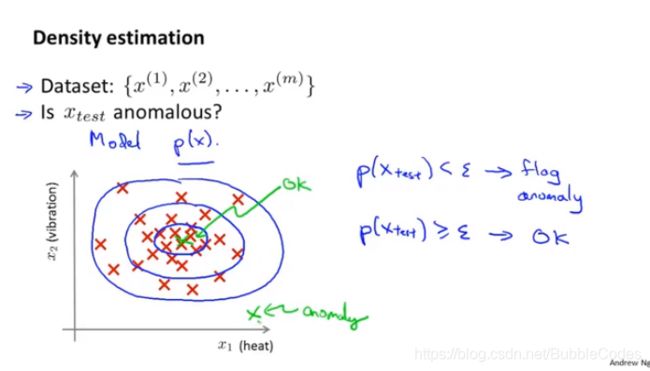
    利用m个n维样本建模, 这里假设每一个维都相互独立（实际上不严格相互独立该算法work well），假设n维中的每一维都服从高斯分布。则有p(X)表达为：

异常检测算法 Anomaly Detection Algorithm

    异常检测算法（基于高斯分布Gaussian distribution ）：
    1、选择n维特征向量
    2、利用训练集数据计算特征向量每一维的参数值
    3、利用得到的概率分布模型计算新样本的概率密度函数的值，并与设置好的阈值ε比较

异常检测anomaly detection 的应用举例
    1、用于检测用户是否出现异常举动，以检测是否出现fraud 或者被盗号。
    2、用于工业中新出厂产品质量检测
    3、用于检测计算机中心的计算机工作是否正常

开发和评估一个异常检测系统 Developing and Evaluating an Anomaly Detection System

    1、使用带标签的数据，训练集使用某类（或者绝大部分是该标签）标签的数据，交叉验证集和测试集

    2、训练集用来拟合概率分布模型，交叉验证集或者测试集用来验证，验证的方法之前讨论过：
    如果数据是very skewed，那么仅仅使用误差度量值是不合适的，通常有其他度量值：
    选择使F₁Score最大的ε

异常检测anomaly detection VS. 监督学习supervised learning

    异常检测算法属于无监督算法，与监督学习有明显的区别。
    疑问：如果我们已经获得了样本和标签，为什么我们不直接使用supervised learning如logistic regression 或者 neural network来做预测，而要使用异常检测问题来判断（预测）？
    个人理解：面对一个very skewed，并且positive的样本很少的情况时，使用监督学习算法无法获得足够多的经验。

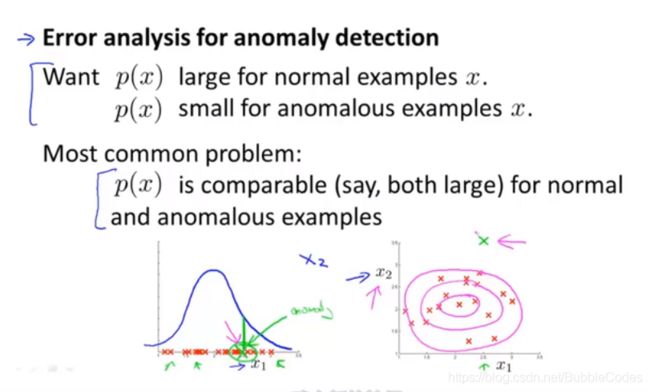
选择要使用的特征 Choosing What Features to Use
    前面的推演有一个假设前提：随机变量服从正态分布（我们使用的是基于正态分布的异常检测，因为正态分布十分常见），如果明显不服从正态分布可以采取以下方案：
    通常来说我们选择符合高斯分布的特征，对于不符合高斯分布的特征（某一维），我们也可以直接选择（一般对算法效果影响不大）或者将其变换为高斯分布的特征。

    在某些情况下：使用较少的特征维度会使得异常数据也会有较高的P(x)，因而被算法认为是正常的。这种情况下误差分析能够帮助我们，我们可以分析那些被算法错误预测为正常的数据，观察能否找出一些问题。我们可能能从问题中发现我们需要增加一些新的特征，增加这些新特征后获得的新算法能够帮助我们更好地进行异常检测。

多元高斯分布 Multivariate Gaussian Distribution

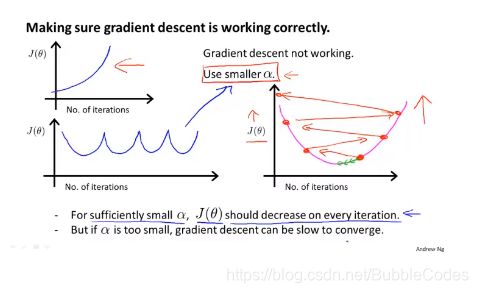
    个人理解：在先前的分析中，我们默认特征变量各个维度之间是相互独立的，在这里我们考虑一种更加普遍的情况：各个特征变量之间的协方差不为0
    引例：

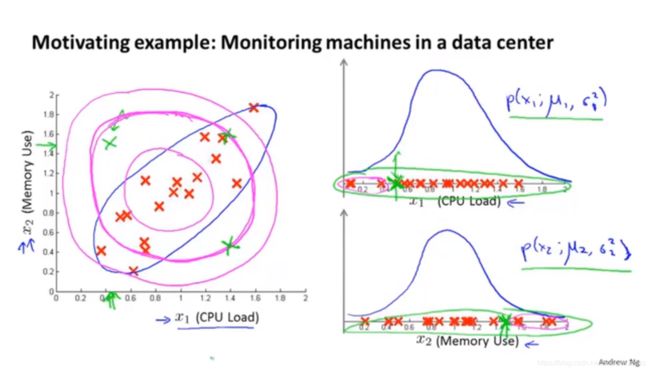
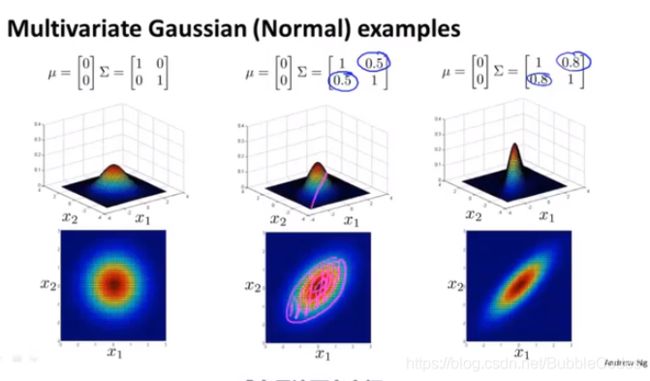
    协方差矩阵正对角线的值为各个维度变量方差，其他位置代表不同维度之间的相关性。使用多元高斯分布运用在异常检测时，没有要求各个特征变量相互独立。
    图形化示例如下图所示：Σ为协方差矩阵，μ为均值矩阵。

多元高斯分布在异常检测中应用


原模型和多元高斯分布的对比：

推荐系统 Recommder System

    为什么学习recommender systems？
    1、对于科技公司来说很重要，影响公司主要收入
    2、特征对于learning algorithm十分重要，recommender system在自动选择特征方面有作用（learning feature）

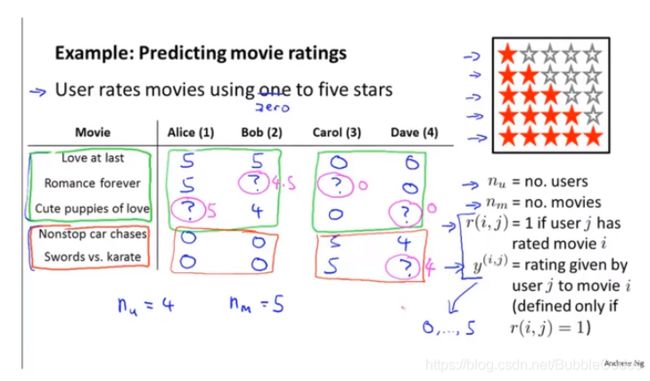
    recommender systems示例：预测电影评分，并推荐你没看过的你可能感兴趣的电影
    recommender system的主要形式：推测出用户喜欢看的电影类型，并推测他给该类型内其他电影的评分，并将它们推荐给用户

基于内容¹⁵的推荐算法 Content Based Recommendation

    假设我们使用线性预测模型:h_θ(x) = θ^T*X

协同过滤 Collaboration Filtering

    在基于内容的推荐系统中，通过电影特征我们可以学习到用户参数（个人理解为用户对电影特征的喜爱程度），即J(θ)；同样的反过来，通过用户参数可以学习到电影的特征，即J(X)。

    但是如果我们既没有用户的参数，也没有电影的特征，这两种方法都不可行了。协同过滤算法可以同时学习这两者。

低秩矩阵分解low rank matrix factorization
    在以及学习获得电影的特征之后（X），我们不难发现Xⁱ之间的距离即是两个电影的相似度。
    从物理意义上讲，矩阵的秩度量的就是矩阵的行列之间的相关性，所以对应了此处电影特征的相似性，相似性越高，秩越小。

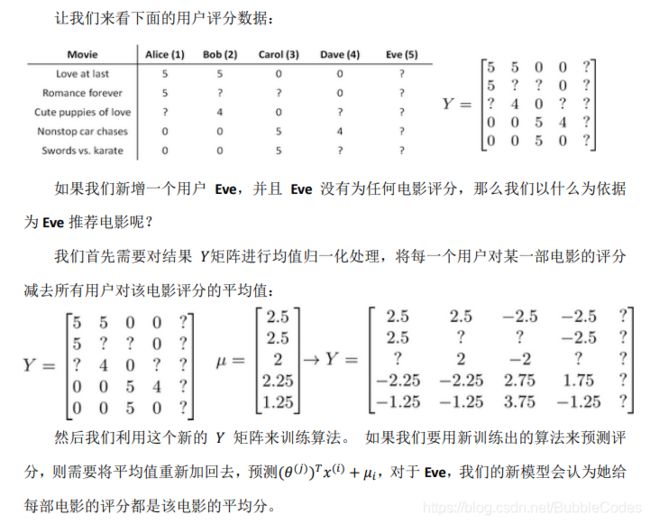
mean normalization 均值归一化
    这里提到了对于一个刚刚进入的用户，他可能还没有对任何电影评过分，那如何对他进行推荐呢？
    思想是使用其他所有用户的某电影平均评分值作为它对某电影的预测评分，θ^T*X+μ，其中θ假设全为0。

大规模机器学习 Large Scale Machine Learning

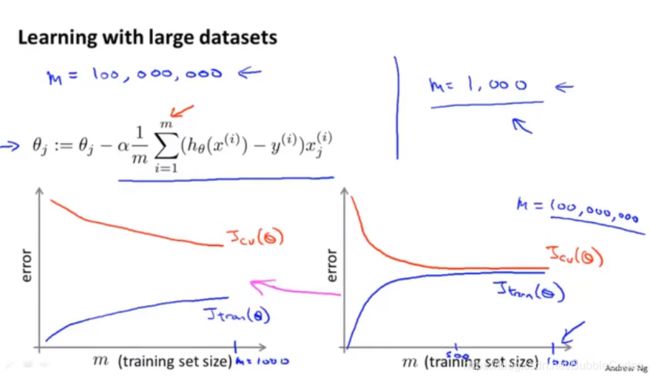
为什么需要海量数据？
    在遇到高方差、过拟合的情况下，使用海量数据对模型的性能提升有所帮助。有时决定一个预测模型好坏的不是算法的差异，而是在于你的数据量是否足够。

随机梯度下降 Stochastic gradient descent

    在遇到海量数据时，使用普通梯度下降算法可能要付出很大的计算代价，而随机梯度下降算法是对普通梯度下降算法在应对海量数据时的改进。
    随机梯度下降减少相较于普通迭代算法减少了迭代次数，它虽然不是每次迭代得到的损失函数都向着全局最优方向， 但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。但是相比于普通迭代算法，这样的方法更快，更快收敛，虽然不是全局最优，但很多时候是我们可以接受的。

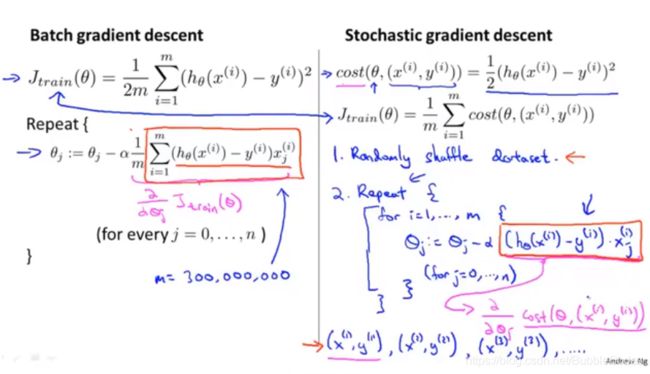
如何确定随机梯度下降算法已经收敛到了合适的位置，如何调节学习速率α？
    在普通梯度下降算法中，我们利用绘制优化代价函数（关于迭代次数的函数）曲线。


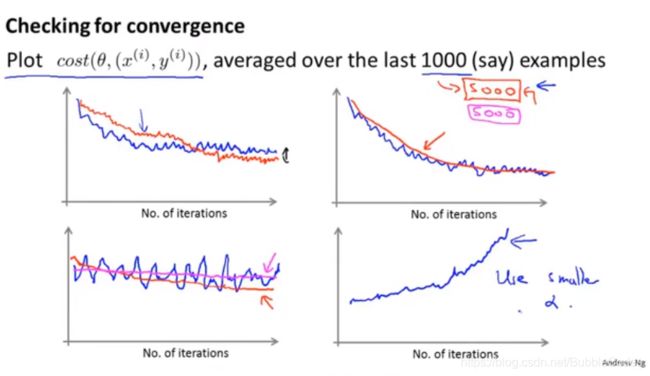
选择α：
    通过迭代次数的增大，逐渐减小α，使得随机梯度下降算法收敛得更好。

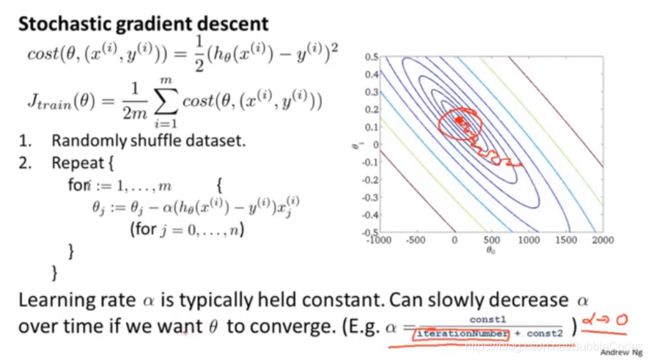
Mini-Batch gradient descent

    Mini-Batch gradient descent可以说是一种折衷的算法，三种梯度下降算法的比较如下图所示：

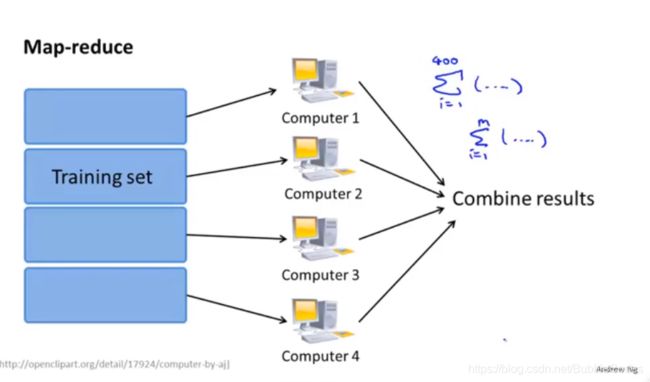
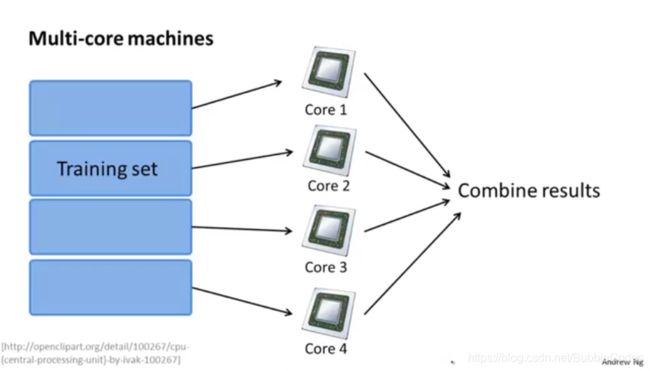
减少映射和数据并行 Map reduce and Data parallelism

    将加法运算分配给各个计算机或者CPU核，以达到加速算法的目的。
    很多高级的线性代数函数库已经能够利用多核 CPU 的多个核心来并行地处理矩阵运算，这也是算法的向量化实现如此重要的缘故（比调用循环快）。

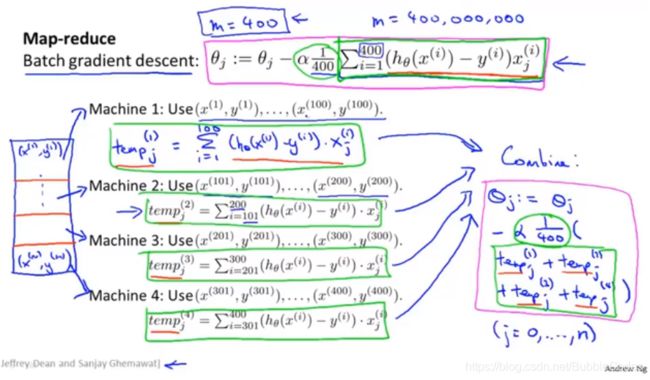
在线学习 online learning

    当我们有连续的数据流时，我们便可以采用在线学习的方式，这种方式具有更强的灵活性。

运用举例：图像文字识别 Application Example：Photo OCR（Optical Character Recognition）

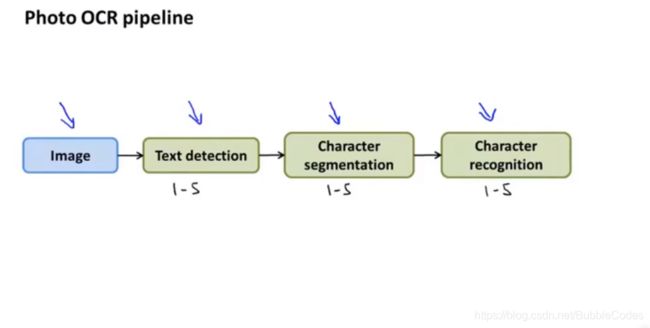
问题描述和OCR.pipeline
    文字检测->字符分割->字符识别

滑动窗口分类器 sliding window classifier

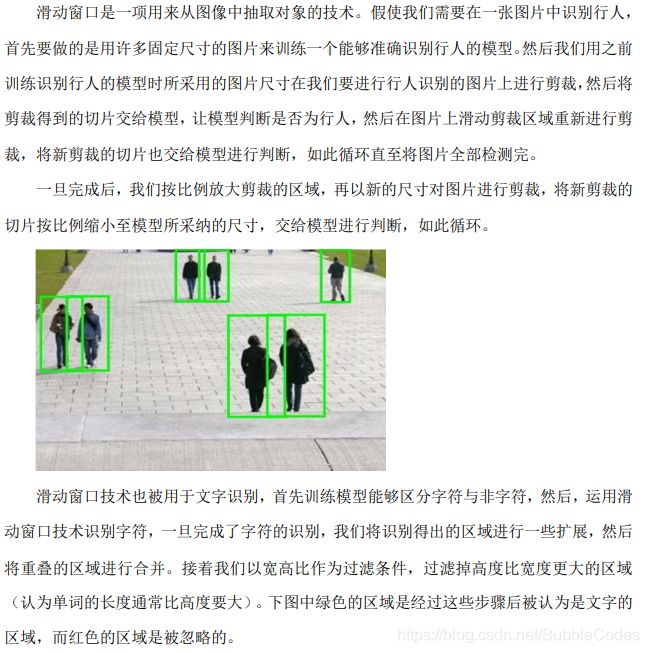
字符检测

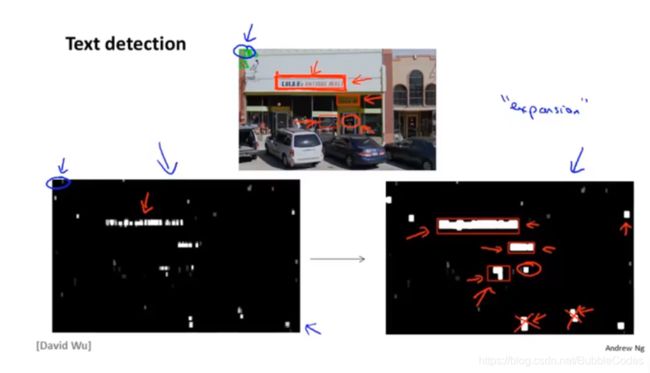
字符分割

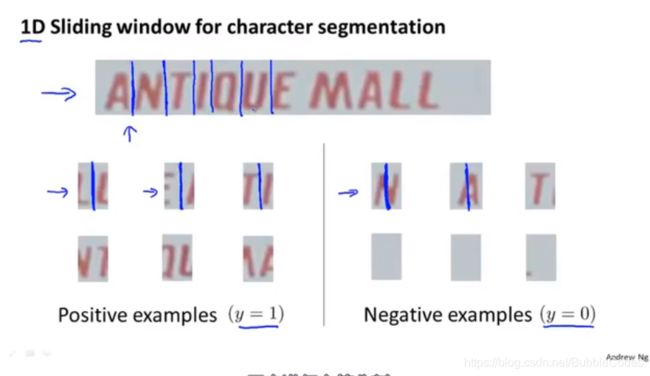
字符识别
    前面介绍过，使用Neural Network或者Logistic Regression做多分类器即可，这里不赘述。

人工数据合成 artificial data synthesis

    1、从零开始自己创造数据
    2、将小数据集变成大数据集

上限分析 ceiling analysis

    另一个例子：

---

1. 梯度：梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。 ↩︎

2. 代价函数cost function（是模型参数的函数），吴恩达老师使用的是平方误差代价函数。 ↩︎

3. 学习速率α：控制我们以多大的幅度更新模型参数。 ↩︎

4. 决策边界 decision bundary：将不同类型的数据用决策边界分开
   使用更加复杂 ↩︎

5. 泛化能力（generalization ability）是指机器学习算法对新鲜样本的适应能力。 ↩︎

6. input layer输入层 ↩︎

7. output layer输出层 ↩︎

8. hidden layer隐藏层 ↩︎

9. 偏置单元bias unit ↩︎

10. 激活函数（Activation Function），就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。 ↩︎

11. matrix of weights权重矩阵：控制前一层到后一层的映射 ↩︎

12.     协方差矩阵covariance matrix Σ=n*n 代表的意义：即随机变量之间的线性相关关系。
        协方差矩阵是对称阵，location（i，j）表示第i和j个变量之间的协方差，协方差表示对应两样本并评估之间的相关程度的。 ↩︎

13. 特征缩放(feature scaling)大致的思路是这样的：梯度下降算法中，在有多个特征的情况下，如果你能确保这些不同的特征都处在一个相近的范围，这样梯度下降法就能更快地收敛。
    使用单一指标对某事物进行评价并不合理，因此需要多指标综合评价方法。多指标综合评价方法，就是把描述某事物不同方面的多个指标综合起来得到一个综合指标，并通过它评价、比较该事物。
    由于性质不同，不同评价指标通常具有不同的量纲和数量级。当各指标相差很大时，如果直接使用原始指标值计算综合指标，就会突出数值较大的指标在分析中的作用、削弱数值较小的指标在分析中的作用。
    为消除各评价指标间量纲和数量级的差异、保证结果的可靠性，就需要对各指标的原始数据进行特征缩放（也有数据标准化、数据归一化的说法，但不准确，所以不推荐这么叫）。
    由于量纲和数量级不同，所以需要特征缩放。特征缩放可以显著提升部分机器学习算法的性能，但它对部分算法没有帮助。 ↩︎

14. 参数估计问题是：在已知随机变量分布函数的形式的情况下，求解其中的一个或者多个未知参数、写出概率密度函数的问题。
        参数估计的方法有两大类：点估计（矩估计、最小二乘估计、极大似然估计等等）和区间估计。 ↩︎

15.     顾名思义，它是利用项目的内在品质或者固有属性来进行推荐，比如音乐的流派、类型，电影的风格、类别等，不需要构建UI矩阵。它是建立在项目的内容信息上作出推荐的，而不需要依据用户对项目的评价意见，更多地需要用机器学习的方法从关于内容的特征描述的事例中得到用户的兴趣资料。我们已经拥有样本即我们已经拥有不同电影的特征。 ↩︎