轨迹(形状)相似性判断与度量方法
目录
- 0. 综述
- 一、基于点方法EDR,LCSS,DTW
- 二、基于形状的方法: Frechet, Hausdorff
-
- 2.2 Hausdorff Distance (豪斯多夫距离)
- 三、基于分段的方法:One Way Distance, LIP distance
-
- 3.1 单向距离(OWD)
- 3.2 LIP
- 四、基于特定任务的方法:TRACLUS, Road Network,grid等
- 参考资料
0. 综述
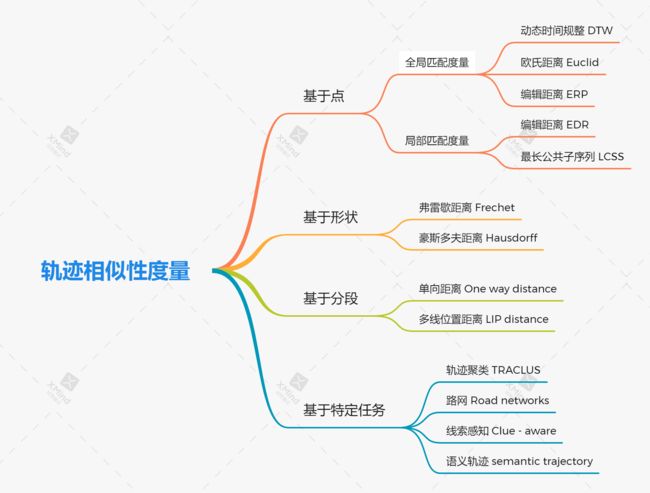
判断两条轨迹的相似性方法有很多
- 基于点方法: EDR,LCSS,DTW等
- 基于形状的方法: Frechet, Hausdorff
- 基于分段的方法:One Way Distance, LIP distance
- 基于特定任务的方法:TRACLUS, Road Network,grid等
一、基于点方法EDR,LCSS,DTW
Eucilid 欧式距离
欧式距离又称欧几里得度量,是一种常用的距离定义。通过计算2条轨迹间对应点的欧氏距离,得到距离序列{d}(i=1,2,…,n),其中n 为2条轨迹中数据点少的轨迹(称为小轨迹)点个数。
欧式距离较为简单和直观,原始轨迹数据经过预处理后,可以利用欧式距离序列的求和、平均值、最大值等指标度量轨迹之间的相似性。
二、基于形状的方法: Frechet, Hausdorff
2.2 Hausdorff Distance (豪斯多夫距离)
空间距离不仅可以用来描述物体的位置分布,还可以用来表示物体之间的相似度。
距离小意味着差异小,相似度高。以空间距离为基础的相似度度量方法有很多,如欧氏距离、曼哈顿距离、闵可夫斯基距离、切比雪夫距离和 Hausdorff 距离等,其中 Hausdorff 距离常用于计算曲线之间的相似度。
假设有两组集合A={a1,…,ap},B={b1,…,bq},则这两个点集合之间的Hausdorff距离定义为
Hausdorff 距离是一种定义两组点集之间距离的方法,可用于描述两组点集之间的相似度。两组点集之间的Hausdorff 距离越大,相似度越低。给定 2 条由若干有序轨迹点构成的轨迹 A = a i A = a_i A=ai , B = b j B = b_j B=bj ,则集合 A与集合 B 的 Hausdorff 距离为
H ( A , B ) = m a x ( h ( A , B ) , h ( B , A ) ) H(A,B)=max(h(A,B),h(B,A)) H(A,B)=max(h(A,B),h(B,A))
h ( A , B ) = m a x a i ∈ A ( m i n b j ∈ B ∥ a i − b j ∥ ) h(A,B)=max_{a_i\in {A}}(min_{b_j\in{B}}\left\| {a_i-b_j}\right\|) h(A,B)=maxai∈A(minbj∈B∥ai−bj∥)
h ( B , A ) = m i n b j ∈ B ( m a x a i ∈ A ∥ b j − a i ∥ ) h(B,A)=min_{b_j\in{B}}(max_{a_i\in {A}}\left\| {b_j-a_i}\right\|) h(B,A)=minbj∈B(maxai∈A∥bj−ai∥)
即h(A,B)实际上首先对点集A中的每个点 a i a_i ai到距离此点 a i a_i ai最近的B集合中点 b j b_j bj之间的距离 ‖ a i − b j ‖ ‖a_i-b_j‖ ‖ai−bj‖ 进行排序,然后取该距离中的最大值作为h(A,B)的值。
式中:H(A, B)是 Hausdorff 距离的最基本形式,称为双向 Hausdorff 距离;h(A, B)是从集合 A 到集合 B 的单向 Hausdorff 距离;h(B, A)为从集合 B 到集合 A 的单向 Hausdorff 距离; ‖·‖ 是两点之间的距离范式(如:L2或Euclidean距离)。
图示及计算流程总结
刚说了那么多,是不是也不是很清楚,只看公式确实是一件不好玩的事情,那我用网上常用的图来说明一下,还有一个比较简单清晰的计算流程。
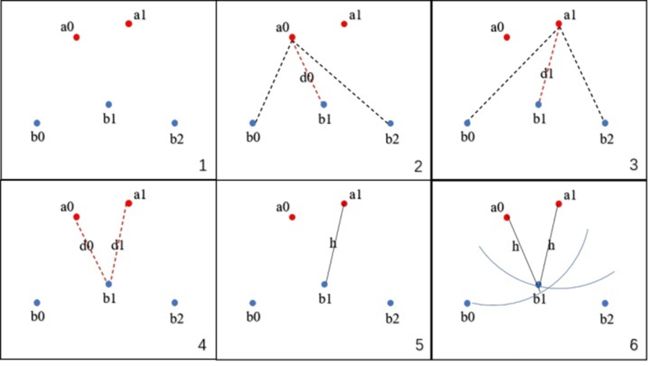
给定两个点集合A{ a0, a1, … }和B{ b0, b1, b2, …}
- 取A集合中的一点a0,计算a0到B集合中所有点的距离,保留最短的距离d0
- 遍历A集合中所有点,图中一共两点a0和a1,计算出d0和d1
- 比较所有的距离{ d0, d1 },选出最长的距离d1
- 这个最长的距离就是h,它是A→B的单向豪斯多夫距离,记为h( A, B )
- 对于A集合中任意一点a,我们可以确定,以点a为圆心,h为半径的圆内部必有B集合中的
- 交换A集合和B集合的角色,计算B→A的单向豪斯多夫距离h( B, A ),选出h( A, B )和h( B, A )中最长的距离,就是A,B集合的双向豪斯多夫距离
相对于传统的距离度量,运用 Hausdorff 距离公式无需对轨迹集进行插值处理,可以直接计算轨迹之间的相似度,避免了给轨迹数据添加噪声,减少了噪声对原始数据的影响;另一方面,由于播发时间间隔不一致,不同船舶产生和记录的 AIS 数据长度不同。Hausdorff 距离可以很好地适用于计算轨迹之间的相似度,因此可以采用 Hausdorff 距离作为轨迹之间的相似度度量。
- 性质:双向Hausdorff距离H(A, B) 是单向 Hausdorff 距离 h(A, B) 和 h(B, A) 两者中的较大者,显然它度量了两个点集的最大不匹配程度。
三、基于分段的方法:One Way Distance, LIP distance
3.1 单向距离(OWD)
OWD 距离的基本思想基于两条轨迹围成的面积,当面积大,说明轨迹之间距离较远,相似度就低;
相反,若围成的面积为0,则说明两条轨迹重合,相似度最高。
3.2 LIP
当某区域面积的周长占总长比重大时权重也自然就大;
当Area均为0时,说明两条轨迹重合没有缝隙,LIP距离为0;
当Area加权和大时,则说明两条轨迹之间缝隙较大,LIP距离也就大。
此外,权重由区域周长占总长比重大决定,也一定程度对抗了噪音点的干扰。
只作用于2维轨迹
四、基于特定任务的方法:TRACLUS, Road Network,grid等
9.CATS(基于线索感知的轨迹相似度)
由于轨迹在采集的时候可能会存在大量采样点缺 失的轨迹段,而对象的同一种运动行为形成的轨迹在空 间上和时间上应该都比较接近,
因此,对于同一模式的轨迹,将他们的采样点相互补 充,得到一条采样完整的轨迹。CATS可以支持局部时间 扭曲,对轨迹的采样率和长度都没有要求,并且对噪声 具有鲁棒性。
10.TRACLUS(轨迹聚类)
通过轨迹聚类找出有代表性的相似轨迹
11.NEAT
轨迹聚类时,考虑路网因素,分三次聚类
12语义轨迹
————————————————
参考资料
[1] 轨迹聚类(一):分段及归组框架(Trajectory Clustering:A Partition-and-Group Framework)) 2016.3
[2] 轨迹聚类(二):分段及归组框架(Trajectory Clustering:A Partition-and-Group Framework) 2016.3
[3] 基于 DBTCAN 算法的船舶轨迹聚类与航路识别 2022.5
[4] Hausdorff Distance(豪斯多夫距离) 2018.3
[5] Hausdorff 距离 2020.3
[6] Metric评价指标-图像分割之豪斯多夫距离(Hausdorff distance )
[7] 最小描述长度(MDL)2012.12
[8] 最小描述长度准则—Minimum Description Length 2017.5
[9] 如何判断两条轨迹(或曲线)的相似度?2017.12
[10] 轨迹相似性度量方法总结 2021.6
[11] 相似性方法调研 2019.1