Rodrigues:旋转矩阵的向量表达
目的:最近看论文,遇到Rodrigues公式,一直没有怎么推导。因此自己推导一遍。
在理解Rodrigues公式,之前需要理解旋转向量的表达方式。
旋转矩阵的向量表达是基于欧拉定理推导的,它有三个参数。而它可以转化为旋转矩阵。这种转化为旋转矩阵的方式被称为Rodrigues公式。
Rotation Vectors
普通认知中,旋转矩阵是 3 × 3 3\times3 3×3的矩阵。这类矩阵有众多约束,具体哪些约束可以查阅资料(后续自己补上)。它只有三个自由度。只要知道那三个参数,剩下的6个参数能够计算,它的表达容易。在一般优化中,使用 Rotation matrix不方便,矩阵的计算复杂且耗时。
定义的来源:
在几何旋转中,任意一个旋转都可以表达为绕着一根轴旋转一定的角度。因此表达方式可以表示为:一根旋转的向量 u → \overrightarrow{u} u,和其旋转的角度 θ \theta θ。因此它可以用4个参数来决定。
假设向量 r → \overrightarrow{r} r为主轴向量,它的旋转的向量从向量 p → \overrightarrow{p} p,旋转角度为 θ \theta θ。如下图:
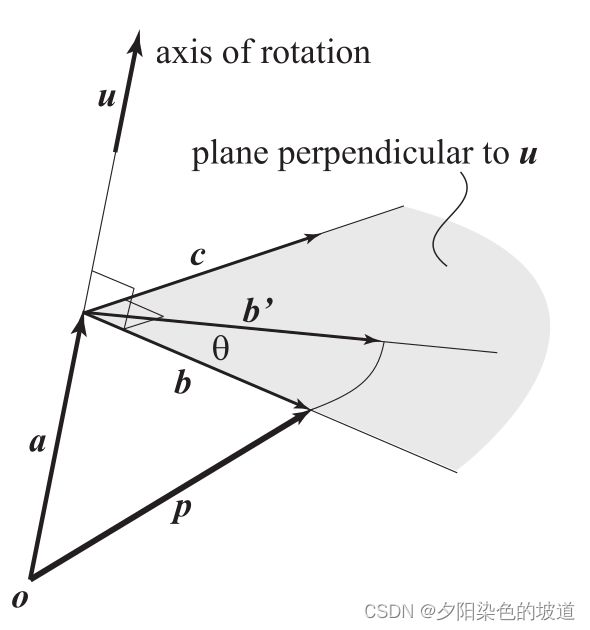
因为 o → \overrightarrow{o} o为原点。简化表达 o p → = p → \overrightarrow{op}=\overrightarrow{p} op=p,其它也使用类似的表达。
从图上可以看到,向量 p → \overrightarrow{p} p绕着轴 u → \overrightarrow{u} u旋转的时候,只和垂直于向量 u → \overrightarrow{u} u有关。因此按照向量 u → \overrightarrow{u} u把它拆分为 a → \overrightarrow{a} a, b → \overrightarrow{b} b,它们分别平面于向量 u → \overrightarrow{u} u和垂直于向量 u → \overrightarrow{u} u。拆分了两个向量,需要计算两个向量。假设 u → \overrightarrow{u} u和 p → \overrightarrow{p} p的夹角为 σ \sigma σ,因此可以得到
c o s σ = u → ⋅ p → ∣ u → ∣ ∣ p → ∣ ( 1 ) cos\sigma=\cfrac{\overrightarrow{u} \cdot \overrightarrow{p}}{|\overrightarrow{u}||\overrightarrow{p}|} \space \space\space\space (1) cosσ=∣u∣∣p∣u⋅p (1)
因为 u → \overrightarrow{u} u为单位向量。因此可以得到
a → = u → ∣ p → ∣ c o s σ = u → ⋅ p → ∣ u → ∣ ∣ p → ∣ ∣ p → ∣ u → = ( u → ⋅ p → ) u → = u → ( u → ⋅ p → ) ( 2 ) \overrightarrow{a}=\overrightarrow{u}|\overrightarrow{p}|cos\sigma=\cfrac{\overrightarrow{u} \cdot \overrightarrow{p}}{|\overrightarrow{u}||\overrightarrow{p}|}|\overrightarrow{p}|\overrightarrow{u}=(\overrightarrow{u} \cdot \overrightarrow{p})\overrightarrow{u} =\overrightarrow{u}(\overrightarrow{u} \cdot \overrightarrow{p}) \space \space\space\space(2) a=u∣p∣cosσ=∣u∣∣p∣u⋅p∣p∣u=(u⋅p)u=u(u⋅p) (2)
通过拆开和合并 ( 2 ) (2) (2)写成向量的形式可以得到:
a → = u → ( u → ⋅ p → ) = u → u → T p → ( 3 ) \overrightarrow{a}=\overrightarrow{u}(\overrightarrow{u} \cdot \overrightarrow{p})=\overrightarrow{u}\overrightarrow{u}^T\overrightarrow{p} \space \space\space\space(3) a=u(u⋅p)=uuTp (3)
对于垂直于向量 u → \overrightarrow{u} u的分量 b → \overrightarrow{b} b
b → = p → − a → = ( 1 − u → u → T ) p → ( 4 ) \overrightarrow{b}=\overrightarrow{p}-\overrightarrow{a}=(1-\overrightarrow{u}\overrightarrow{u}^T)\overrightarrow{p} \space \space\space\space(4) b=p−a=(1−uuT)p (4)
因为从向量 b → \overrightarrow{b} b旋转到向量 b ′ → \overrightarrow{b'} b′,需要另一个向量 c → \overrightarrow{c} c,它是垂直于向量 u → \overrightarrow{u} u和向量 p → \overrightarrow{p} p所在的平面,且它的长度和向量 b → \overrightarrow{b} b一样。
满足: ∣ b → ∣ = ∣ c → ∣ |\overrightarrow{b}|=|\overrightarrow{c}| ∣b∣=∣c∣
通过三角行垂直公式得到:
∣ b → ∣ = ∣ u → ∣ ∣ p → ∣ s i n σ ( 5 ) |\overrightarrow{b}|=|\overrightarrow{u}||\overrightarrow{p}|sin\sigma \space \space\space\space(5) ∣b∣=∣u∣∣p∣sinσ (5)
通过叉乘,可以设计向量 c → \overrightarrow{c} c:
c → = u → × p → = ( ∣ u → ∣ ∣ p → ∣ s i n σ ) c → ∣ c → ∣ = ( ∣ u → ∣ ∣ p → ∣ s i n σ ) n → ( 6 ) \overrightarrow{c} = \overrightarrow{u} \times \overrightarrow{p} =(|\overrightarrow{u}|| \overrightarrow{p}|sin\sigma) \cfrac{\overrightarrow{c}}{|\overrightarrow{c}|} = (|\overrightarrow{u}|| \overrightarrow{p}|sin\sigma)\overrightarrow{n} \space \space\space\space(6) c=u×p=(∣u∣∣p∣sinσ)∣c∣c=(∣u∣∣p∣sinσ)n (6)
其中 n → = c → ∣ c → ∣ \overrightarrow{n}=\cfrac{\overrightarrow{c}}{|\overrightarrow{c}|} n=∣c∣c单位向量。因此 ∣ c → ∣ = ∣ u → ∣ ∣ p → ∣ s i n σ |\overrightarrow{c}| =|\overrightarrow{u}||\overrightarrow{p}|sin\sigma ∣c∣=∣u∣∣p∣sinσ
通过计算它们的模,发现它们是相等的。
上面的公式 ( 6 ) (6) (6),将在下一篇blog介绍。后面更新它们的链接
因此可以得到 p → \overrightarrow{p} p旋转后得到的向量 p ′ → \overrightarrow{p'} p′为:
b ′ → = b → c o s θ + c → s i n θ ( 7 ) \overrightarrow{b'}=\overrightarrow{b}cos\theta+\overrightarrow{c}sin\theta \space \space\space\space(7) b′=bcosθ+csinθ (7)
然后通过向量加法
p ′ → = a → + b ′ → = a → + b → c o s θ + c → s i n θ = u → u → T p → + ( 1 − u → u → T ) p → c o s θ + ( u → × p → ) s i n θ = [ I c o s θ + ( 1 − c o s θ ) u → u → T + u → × s i n θ ] p → ( 8 ) \overrightarrow{p'}=\overrightarrow{a} + \overrightarrow{b'}= \overrightarrow{a} + \overrightarrow{b}cos\theta+\overrightarrow{c}sin\theta \\ = \overrightarrow{u}\overrightarrow{u}^T\overrightarrow{p}+(1-\overrightarrow{u}\overrightarrow{u}^T)\overrightarrow{p}cos\theta+(\overrightarrow{u} \times \overrightarrow{p})sin\theta \\ = [Icos\theta+(1-cos\theta)\overrightarrow{u}\overrightarrow{u}^T+\overrightarrow{u} \times sin\theta]\overrightarrow{p} \space \space\space\space(8) p′=a+b′=a+bcosθ+csinθ=uuTp+(1−uuT)pcosθ+(u×p)sinθ=[Icosθ+(1−cosθ)uuT+u×sinθ]p (8)
通过公式 ( 8 ) (8) (8)可以得到一个向量 p → \overrightarrow{p} p围绕向量 u → \overrightarrow{u} u得到旋转 θ \theta θ新的向量 p ′ → \overrightarrow{p'} p′的公式,其中 R = I c o s θ + ( 1 − c o s θ ) u → u → T + u → × s i n θ R=Icos\theta+(1-cos\theta)\overrightarrow{u}\overrightarrow{u}^T+\overrightarrow{u} \times sin\theta R=Icosθ+(1−cosθ)uuT+u×sinθ。它也是Rodrigues公式。
还有一种特殊情况,如果 u → = [ 0 , 0 , 0 ] T \overrightarrow{u}=[0,0,0]^T u=[0,0,0]T,得到的旋转矩阵为 I I I
上面的公式也可以反推(因为它不太常用),后面再补上。
参考资料为:
Vector Representation of rotations的论文。