聚类—K-means算法
活动地址:CSDN21天学习挑战赛
聚类分析概述
-
什么是聚类
-
是把数据对象集合按照相似性划分成多个子集的过程
-
每个子集是一个簇,使得簇中的对象彼此相似,但与其他簇的对象不相似
即同簇相似,异簇相别
-
-
聚类是无监督学习,训练集中无类标号信息
基本聚类方法
- 划分方法
- 层次方法
- 基于密度的方法
划分方法
-
将有n个对象的数据集D划分成k个簇,并且 k ≤ n k\leq n k≤n
满足一下要求:
- 每个簇至少包含一个对象
- 每个对象属于且仅属于一个簇
-
基本思想:
- 首先创建一个初始K划分(K为要构造的划分数)
- 然后不断迭代地计算各个簇的聚类中心并依新的聚类中心调整聚类情况,直至收敛
-
目标:
- 同一个簇中的对象之间尽可能“接近”或相关
- 不同簇中的对象之间尽可能“远离”或不同
-
启发式方法:
-
定义: E = ∑ i = 1 k ∑ p ∈ C i ( d ( p , c ) i ) 2 表示对数据里的 K 个簇,每个簇的点 p 到聚簇的中心点 c 的距离尽可能的小 这个 E 值越小,说明簇越紧凑 定义: E=\sum_{i=1}^k\sum_{p\in C_i}(d(p,c)_i)^2\\ 表示对数据里的K个簇,每个簇的点p到聚簇的中心点c的距离尽可能的小\\ 这个E值越小,说明簇越紧凑 定义:E=i=1∑kp∈Ci∑(d(p,c)i)2表示对数据里的K个簇,每个簇的点p到聚簇的中心点c的距离尽可能的小这个E值越小,说明簇越紧凑
-
K-均值(K-means)
- 每个簇用该簇中对象的均值来表示
- 基于质心的技术
-
K-中心点(K-medoids)
- 每个簇用接近簇中心的一个对象来表示
- 基于代表对象的技术
-
K-均值算法
适用性:
- 这些启发式算法适合发现中小规模数据库中的球状聚类
- 对于大规模数据库和处理任意形状的聚类,这些算法需要进一步扩展
算法流程:
-
从数据集中随机取K个样本作为初始的聚类中心
C = c 1 , c 2 , . . . , c k C={c_1,c_2,...,c_k} C=c1,c2,...,ck
-
针对数据集中每个样本 x i x_i xi,计算它到K个聚类中心的距离,并将其分到距离最小的聚类中心对应的类中
-
针对每个类别的 c i c_i ci,重新计算其聚类中心
聚类中心计算的方法就是簇中每个对象的平均值
c i = 1 ∣ c i ∣ ∑ x ∈ c i x c_i=\frac{1}{|c_i|}\sum_{x\in c_i}x ci=∣ci∣1x∈ci∑x
- 重复第2和第3 步骤,直到 ∑ i = 0 n min ( ∥ x j − c i ∥ 2 ) \sum_{i=0}^n\min(\|x_j-c_i\|^2) ∑i=0nmin(∥xj−ci∥2)小于特定的阈值
示例:
- K的选择,可以通过散点图,观察其分布,大概分为几个簇,则K取多少
K-均值特点
优点:
- 聚类时间快
- 当结果簇是密集的,而簇与簇之间区别明显时,效果较好
- 相对可扩展和有效,能对大数据集进行高效划分
缺点:
- 用户必须事先指定聚类簇的个数
- 常常终止于局部最优
- 只适用于数值属性聚类(计算均值有意义)
- 对噪声和异常数据也很敏感
- 不同的初始值,结果可能不同
- 不适合发现非凸面形状的簇
K-均值案例
KMeans中初始簇规模估计正确
- 我们要先估计正确这个K值
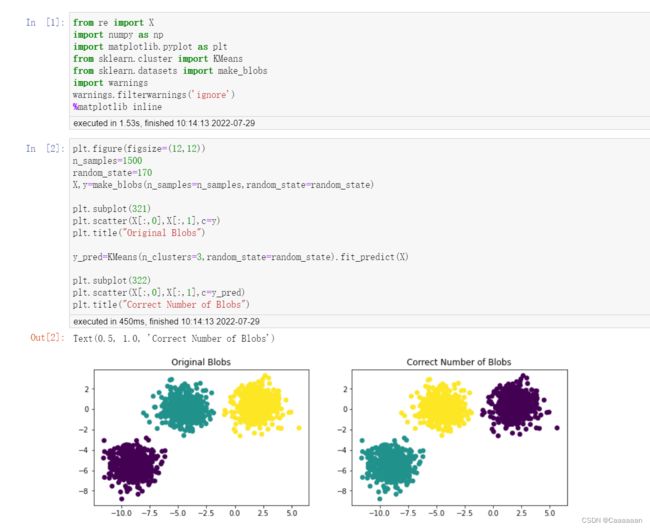
from re import X
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
plt.figure(figsize=(12,12))
n_samples=1500
random_state=170
X,y=make_blobs(n_samples=n_samples,random_state=random_state)
plt.subplot(321)
plt.scatter(X[:,0],X[:,1],c=y)
plt.title("Original Blobs")
y_pred=KMeans(n_clusters=3,random_state=random_state).fit_predict(X)
plt.subplot(322)
plt.scatter(X[:,0],X[:,1],c=y_pred)
plt.title("Correct Number of Blobs")
- 运行结果
- 则可以预测出,簇为3
数据分布形状对分簇结果的影响
前面提及,聚类算法对球状分布的效果良好
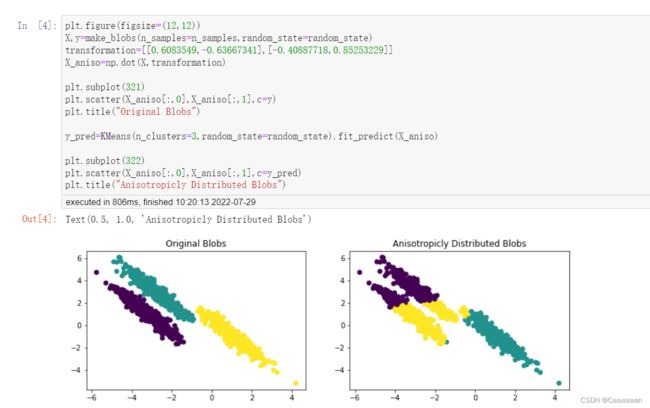
X,y=make_blobs(n_samples=n_samples,random_state=random_state)
transformation=[[0.6083549,-0.63667341],[-0.40887718,0.85253229]]
X_aniso=np.dot(X,transformation)
plt.subplot(321)
plt.scatter(X_aniso[:,0],X_aniso[:,1],c=y)
plt.title("Original Blobs")
y_pred=KMeans(n_clusters=3,random_state=random_state).fit_predict(X_aniso)
plt.subplot(322)
plt.scatter(X_aniso[:,0],X_aniso[:,1],c=y_pred)
plt.title("Anisotropicly Distributed Blobs")
- 运行结果
- 我们可以观察到原来的簇,是三类条形,非球形的紧密簇
所以,可以观察到,在这样的数据分布下,聚类的表现并不好
数据分散程度对分簇结果的影响
X_varied,y_varied=make_blobs(n_samples=n_samples,cluster_std=[1.0,2.5,0.5],random_state=random_state)
plt.subplot(321)
plt.scatter(X_varied[:,0],X_varied[:,1],c=y_varied)
plt.title("Original Blobs")
y_pred=KMeans(n_clusters=3,random_state=random_state).fit_predict(X_varied)
plt.subplot(322)
plt.scatter(X_varied[:,0],X_varied[:,1],c=y_pred)
plt.title("Unequal Variance")
- 运行结果
随机初始种子的影响
因为我们一开始的K个样本是随机选取的,随机的选取,对最后的结果有一定的影响
n_samples=30
random_state=50
X,y=make_blobs(n_samples=n_samples,random_state=random_state)
X_varied,y_varied=make_blobs(n_samples=n_samples,cluster_std=[1,2,1],random_state=random_state)
plt.subplot(321)
plt.scatter(X_varied[:,0],X_varied[:,1],c=y)
plt.title("Original Blobs")
y_pred=KMeans(init='random',n_clusters=3,n_init=1).fit_predict(X_varied)
plt.subplot(322)
plt.scatter(X_varied[:,0],X_varied[:,1],c=y_pred)
plt.title("Unequal Variance")
y_pred=KMeans(init='random',n_clusters=3,n_init=1).fit_predict(X_varied)
plt.subplot(323)
plt.scatter(X_varied[:,0],X_varied[:,1],c=y_pred)
plt.title("Unequal Variance")
y_pred=KMeans(init='random',n_clusters=3,n_init=1).fit_predict(X_varied)
plt.subplot(324)
plt.scatter(X_varied[:,0],X_varied[:,1],c=y_pred)
plt.title("Unequal Variance")
- 运行结果
K-modes算法
K-众数算法,解决K-均值算法无法处理标称离散变量的问题
通过计算离散数据出现次数最多的那个数,来作为类中心点
K-means++算法
解决初始点选择不好,会出现聚类效果不好的情况
基本原理
- 从输入的数据点集合中随机选择一个点作为第一个聚类中心
- 对于数据集中的每一个点X,计算其与聚类中心的距离D(X)
- 选择一个D(X)最大的点作为新的聚类中心
- 重复2和3步直到K个聚类中心被选出
- 利用K个初始聚类中心,继续运行K-Means
- 贪心策略:选择尽可能远的点作为新的聚类中心
K-中心点算法
- 解决K-means算法对离群点的敏感问题
影响结果的例子:
比如说,一维空间中存在7个点1 2 3 8 9 10 25(25是离群点)
- 设置K=2,直觉应该划分为(1,2,3)(8,9,10,25)两个类别
- 按照划分方法聚类质量评价准则,最小化E值
E = ∑ i = 1 k ∑ p ∈ C i ( d ( p , c i ) ) 2 E=\sum_{i=1}^k\sum_{p\in C_i}(d(p,c_i))^2 E=i=1∑kp∈Ci∑(d(p,ci))2
得(1,2,3)(8,9,10,25)聚类的E值为:
( 1 − 2 ) 2 + ( 2 − 2 ) 2 + ( 3 − 2 ) 2 + ( 8 − 13 ) 2 + ( 9 − 13 ) 2 + ( 10 − 13 ) 2 + ( 25 − 13 ) 2 = 196 (1-2)^2+(2-2)^2+(3-2)^2+(8-13)^2+(9-13)^2+(10-13)^2+(25-13)^2=196 (1−2)2+(2−2)2+(3−2)2+(8−13)2+(9−13)2+(10−13)2+(25−13)2=196
而(1,2,3,8)(9,10,25)聚类的E值为:
( 1 − 3.5 ) 2 + ( 2 − 3.5 ) 2 + ( 3 − 3.5 ) 2 + ( 8 − 3.5 ) 2 + ( 9 − 14.67 ) 2 + ( 10 − 14.67 ) 2 + ( 25 − 14.67 ) 2 = 189.67 (1-3.5)^2+(2-3.5)^2+(3-3.5)^2+(8-3.5)^2+(9-14.67)^2+(10-14.67)^2+(25-14.67)^2=189.67 (1−3.5)2+(2−3.5)2+(3−3.5)2+(8−3.5)2+(9−14.67)2+(10−14.67)2+(25−14.67)2=189.67
- 因此算法会根据E值,错误聚类,进而影响K-means算法的一个正确性
基本原理
-
选用簇中位置最中心的实际对象即中心点作为参照点
-
基于最小化所有对象与其参照点之间的相异度之和的原则来划分
采用绝对误差标准
E = ∑ i = 1 k ∑ p ∈ C i ∣ p − o i ∣ E=\sum_{i=1}^k\sum_{p\in C_i}|p-o_i| E=i=1∑kp∈Ci∑∣p−oi∣