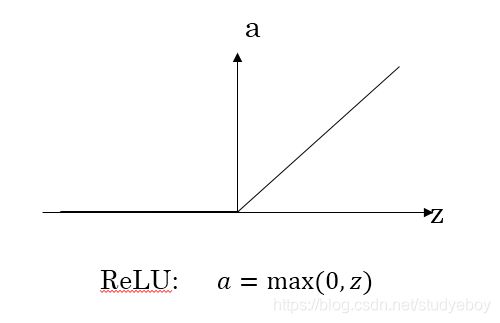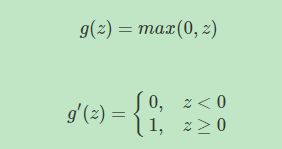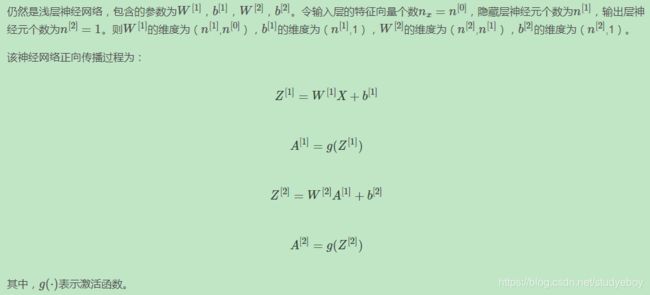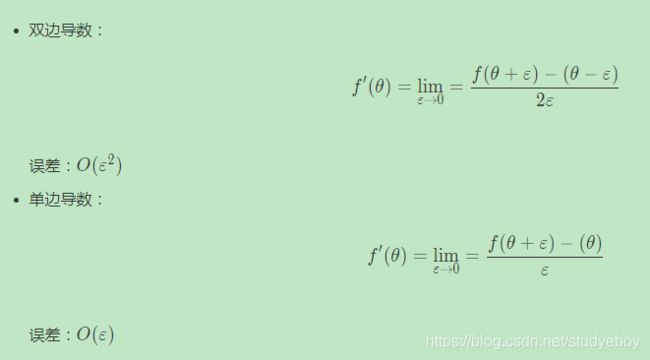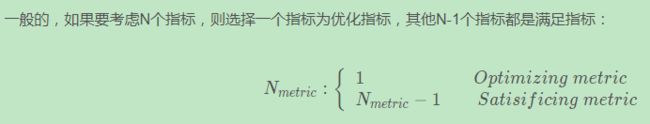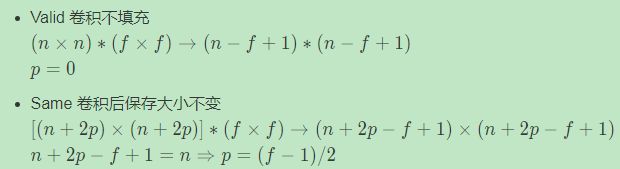吴恩达深度学习——读书笔记
神经网络和深度学习
深度学习概述
深度学习(Deep Learning)是更复杂的神经网络(Neural Network)。
这是一个基本的神经网络模型结构。在训练的过程中,只要有足够的输入x和输出y,就能训练出较好的神经网络模型,该模型在此类房价预测问题中,能够得到比较准确的结果。
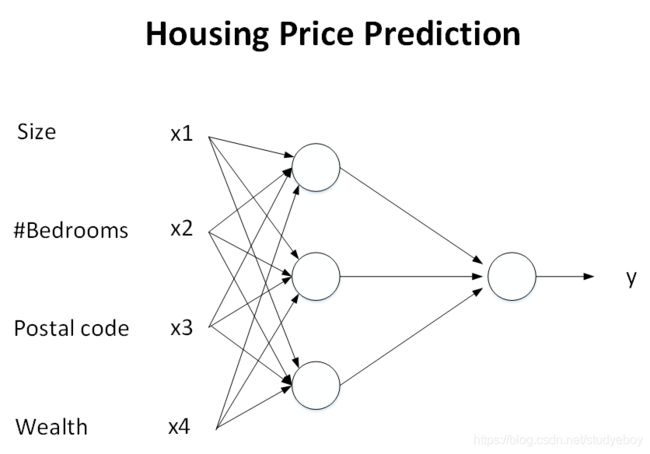
左边是输入层,由人工输入,中间是隐藏层,连接数很高,神经网络自己决定每个节点具体是什么,右边是输出层,神经网络非常擅长计算从x到y的精准映射函数。
神经网络模型创造的价值基本上都是基于监督式学习(Supervised Learning)的。监督式学习与非监督式学习本质区别就是是否已知训练样本的输出y。在实际应用中,机器学习解决的大部分问题都属于监督式学习,神经网络模型也大都属于监督式学习。
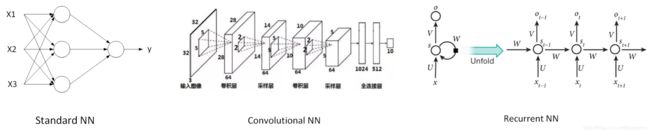
CNN和RNN是比较常用的神经网络模型。下图给出了Standard NN,Convolutional NN和Recurrent NN的神经网络结构图。
数据类型一般分为两种:Structured Data和Unstructured Data。
- 结构化数据
通常指的是有实际意义的数据。例如:房价预测中的size,#bedrooms,price等。易于机器理解。 - 非结构化的数据
通常指的是比较抽象的数据。例如:Audio,Image或者Text等。易于人类理解。

基于深度学习,机器越来越容易理解非结构化数据。
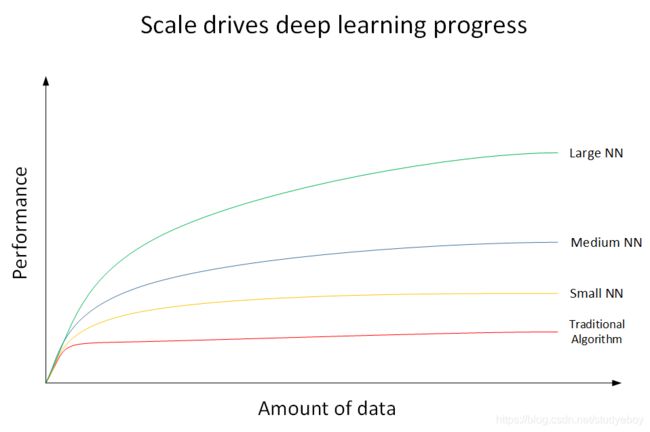
- 红色曲线代表了传统机器学习算法的表现,例如是SVM,logistic regression,decision tree等。当数据量比较小的时候,传统学习模型的表现是比较好的。但是当数据量很大的时候,其表现很一般,性能基本趋于水平。
- 黄色曲线代表了规模较小的神经网络模型(Small NN)。它在数据量较大时候的性能优于传统的机器学习算法。
- 蓝色曲线代表了规模中等的神经网络模型(Media NN),它在在数据量更大的时候的表现比Small NN更好。
- 绿色曲线代表更大规模的神经网络(Large NN),即深度学习模型。从图中可以看到,在数据量很大的时候,它的表现仍然是最好的,而且基本上保持了较快上升的趋势。
近些年来,由于数字计算机的普及,人类进入了大数据时代,每时每分,互联网上的数据是海量的、庞大的。如何对大数据建立稳健准确的学习模型变得尤为重要。传统机器学习算法在数据量较大的时候,性能一般,很难再有提升。然而,深度学习模型由于网络复杂,对大数据的处理和分析非常有效。所以,近些年来,在处理海量数据和建立复杂准确的学习模型方面,深度学习有着非常不错的表现。然而,在数据量不大的时候,例如上图中左边区域,深度学习模型不一定优于传统机器学习算法,性能差异可能并不大。
所以说,现在深度学习如此强大的原因归结为三个因素:
- Data 数据
数据量几何级数增加 - Computation 计算能力
GPU出现、计算机运算能力的大大提升,使得深度学习能够应用得更加广泛。 - Algorithms 算法
算法上的创新和改进让深度学习的性能和速度也大大提升。
神经网络基础之逻辑回归
逻辑回归(Logistic Regression)是一个二分分类(Binary Classification)算法,逻辑回归的目标是最小化其预测与训练数据之间的误差。为了训练逻辑回归模型中的参数 w w w和 b b b,需要定义一个成本函数。
成本函数(cost function)是针对整个训练集的,衡量参数 w w w和 b b b在整个训练集上的效果。
损失函数或误差函数(loss function or error function)是针对单个训练样本进行定义的。可以用来衡量算法的效果,衡量预测输出值与实际值有多接近。
梯度下降法的核心是最小化成本函数。使用梯度下降法可以找到一个函数的局部极小值。
二分类(Binary Classification)
逻辑回归模型一般用来解决二分类(Binary Classification)问题。二分类就是输出y只有{0,1}两个离散值(也有{-1,1}的情况)。以一个图像识别问题为例,判断图片中是否有猫存在,0代表noncat,1代表cat。

这是一个典型的二分类问题。一般来说,彩色图片包含RGB三个通道。例如该cat图片的尺寸为(64,64,3)。在神经网络模型中,我们首先要将图片输入 x x x(维度是(64,64,3))转化为一维的特征向量(feature vector)。方法是每个通道一行一行取,再连接起来。由于64x64x3=12288,则转化后的输入特征向量维度为(12288,1)。此特征向量 x x x是列向量,维度一般记为 n x n_x nx。
如果训练样本共有 m m m张图片,那么整个训练样本 X X X组成了矩阵,维度是 ( n x , m ) (n_x,m) (nx,m)。注意,这里矩阵 X X X的行 n x n_x nx代表了每个样本 x ( i ) x^{(i)} x(i)特征个数,列 m m m代表了样本个数。所有训练样本的输出Y也组成了一维的行向量,写成矩阵的形式后,它的维度就是 ( 1 , m ) (1,m) (1,m)。
逻辑回归(Logistic Regression)
逻辑回归中,预测值 h ^ = P ( y = 1 ∣ x ) \hat h=P(y=1 | x) h^=P(y=1∣x)表示为1的概率,取值范围在[0,1]之间。这是其与二分类模型不同的地方。使用线性模型,引入参数 w w w和 b b b。权重 w w w的维度是 ( n x , 1 ) (n_x,1) (nx,1), b b b是一个常数项。这样,逻辑回归的线性预测输出可以写成:
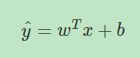
上式的线性输出区间为整个实数范围,而逻辑回归要求输出范围在[0,1]之间,所以还需要对上式的线性函数输出进行处理。方法是引入Sigmoid函数,让输出限定在[0,1]之间。这样,逻辑回归的预测输出就可以完整写成:
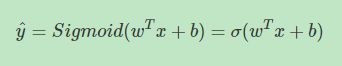
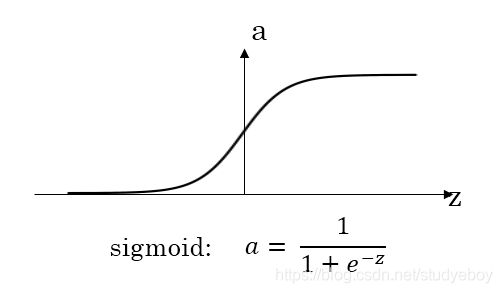
Sigmoid函数是一种非线性的S型函数,输出被限定在[0,1]之间,通常被用在神经网络中当作激活函数(Activation function)使用。Sigmoid函数的表达式和曲线如下所示:
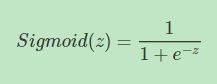

从Sigmoid函数曲线可以看出,当z值很大时,函数值趋向于1;当z值很小时,函数值趋向于0。且当z=0时,函数值为0.5。还有一点值得注意的是,Sigmoid函数的一阶导数可以用其自身表示:
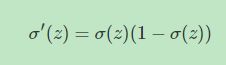
这样,通过Sigmoid函数,就能够将逻辑回归的输出限定在[0,1]之间了。
逻辑回归成本函数(Logistic Regression Cost Function)
逻辑回归中, w w w和 b b b都是未知参数,需要反复训练优化得到。因此,我们需要定义一个cost function,包含了参数 w w w和 b b b。通过优化cost function,当cost function取值最小时,得到对应的 w w w和 b b b。
先从单个样本出发,我们希望该样本的预测值 y ^ \hat y y^与真实值越相似越好。我们把单个样本的cost function用Loss function来表示。Loss function的原则和目的就是要衡量预测输出 y ^ \hat y y^与真实样本输出 y y y的接近程度。平方错误其实也可以,只是它是non-convex的,不利于使用梯度下降算法来进行全局优化。因此,我们可以构建另外一种Loss function,且是convex的,如下所示:
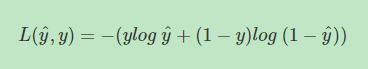

对于m个样本,通常使用上标来表示对应的样本。例如 ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i))表示第 i i i个样本。定义Cost function是 m m m个样本的Loss function的平均值,反映了 m m m个样本的预测输出 y ^ \hat y y^与真实样本输出 y y y的平均接近程度。Cost function可表示为:

Cost function是关于待求系数 w w w和 b b b的函数。我们的目标就是迭代计算出最佳的 w w w和 b b b值,最小化Cost function,让Cost function尽可能地接近于零。
其实逻辑回归问题可以看成是一个简单的神经网络,只包含一个神经元。
梯度下降(Gradient Descent)
使用梯度下降(Gradient Descent)算法来计算出合适的 w w w和 b b b值,从而最小化 m m m个训练样本的Cost function,即 J ( w , b ) J(w,b) J(w,b)。
由于 J ( w , b ) J(w,b) J(w,b)是convex function,梯度下降算法是先随机选择一组参数 w w w和 b b b值,然后每次迭代的过程中分别沿着 w w w和 b b b的梯度(偏导数)的反方向前进一小步,不断修正 w w w和 b b b。每次迭代更新 w w w和 b b b后,都能让 J ( w , b ) J(w,b) J(w,b)更接近全局最小值。梯度下降的过程如下图所示。
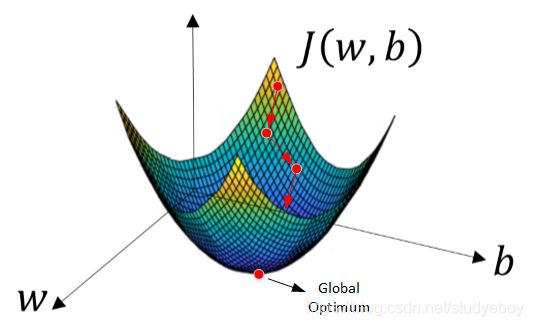

梯度下降算法能够保证每次迭代 w w w和 b b b都能向着 J ( w , b ) J(w,b) J(w,b)全局最小化的方向进行。
计算图(Computation graph)
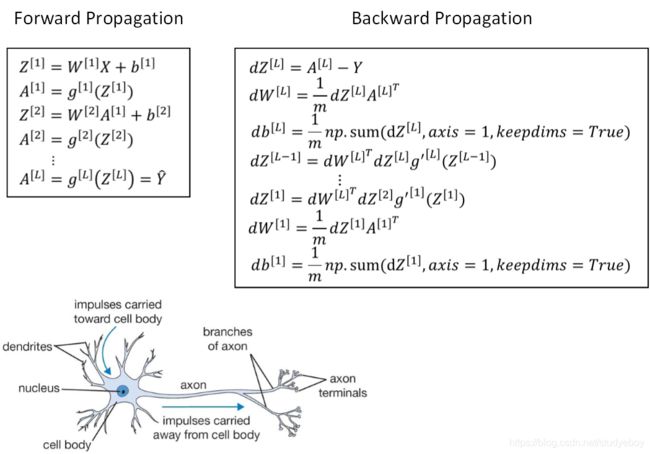
整个神经网络的训练过程实际上包含了两个过程:正向传播(Forward Propagation)和反向传播(Back Propagation)。正向传播是从输入到输出,由神经网络计算得到预测输出的过程;反向传播是从输出到输入,对参数 w w w和 b b b计算梯度的过程。
假如Cost function为J(a,b,c)=3(a+bc),包含a,b,c三个变量。我们用u表示bc,v表示a+u,则J=3v。它的计算图可以写成如下图所示:
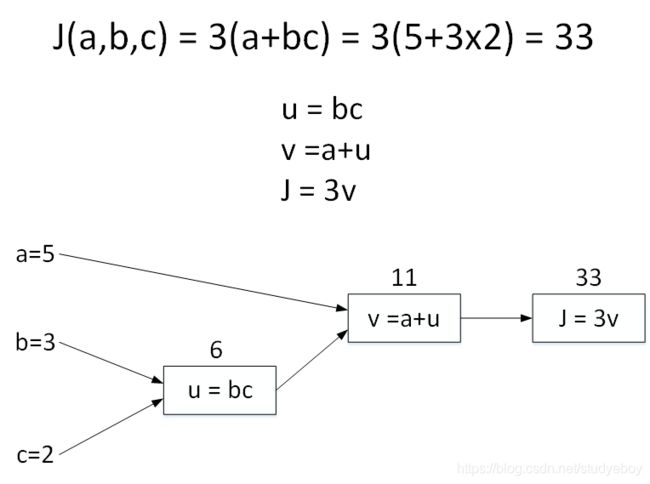
令a=5,b=3,c=2,则u=bc=6,v=a+u=11,J=3v=33。计算图中,这种从左到右,从输入到输出的过程就对应着神经网络或者逻辑回归中输入与权重经过运算计算得到Cost function的正向过程。
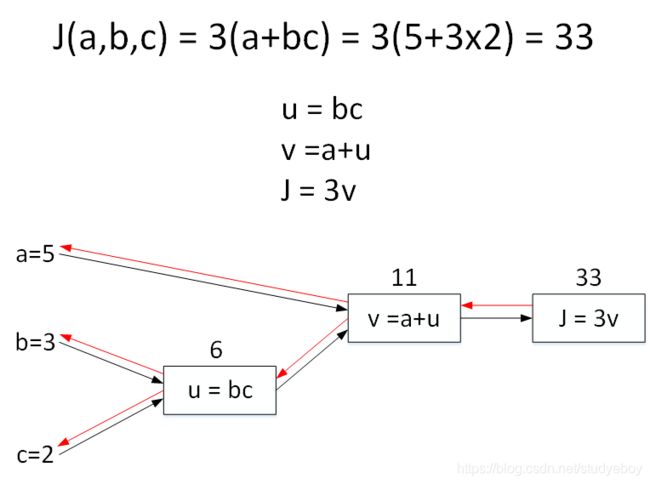
反向传播(Derivatives with a Computation Graph)
反向传播(Back Propagation),即计算输出对输入的偏导数。还是上个计算图的例子,输入参数有3个,分别是a,b,c。

逻辑回归梯度下降(Logistic Regression Gradient Descent)
对逻辑回归进行梯度计算。对单个样本而言,逻辑回归Loss function表达式如下:
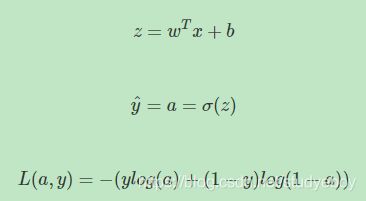
首先,该逻辑回归的正向传播过程非常简单。根据上述公式,例如输入样本 x x x有两个特征 ( x 1 , x 2 ) (x1,x2) (x1,x2),相应的权重 w w w维度也是2,即 ( w 1 , w 2 ) (w1,w2) (w1,w2)。则 z = w 1 x 1 + w 2 x 2 + b z=w1x1+w2x2+b z=w1x1+w2x2+b,最后的Loss function如下所示:

然后,计算该逻辑回归的反向传播过程,即由Loss function计算参数 w w w和 b b b的偏导数。推导过程如下:
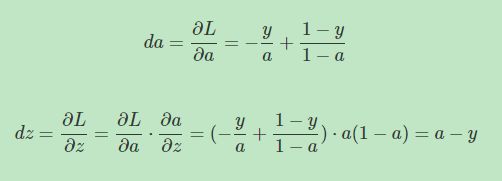
知道了 d z dz dz之后,就可以直接对 w 1 , w 2 w1,w2 w1,w2和 b b b进行求导了。
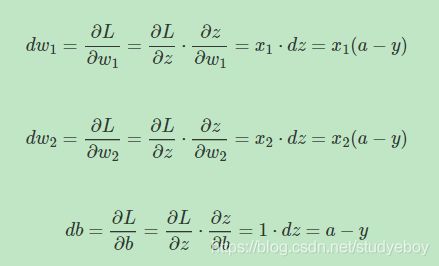
则梯度下降算法可表示为:
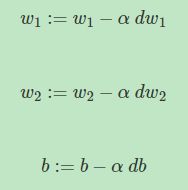

多样本梯度下降(Gradient descent on m examples)
如果有 m m m个样本,其Cost function表达式如下:
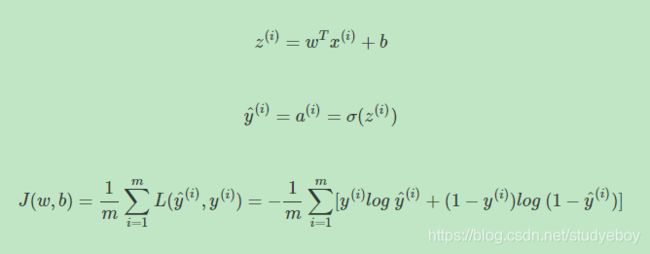
Cost function关于 w w w和 b b b的偏导数可以写成和平均的形式:

这样,每次迭代中 w w w和 b b b的梯度有 m m m个训练样本计算平均值得到。
经过每次迭代后,根据梯度下降算法, w w w和 b b b都进行更新:
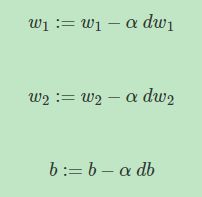
这样经过 n n n次迭代后,整个梯度下降算法就完成了。
在上述的梯度下降算法中,我们是利用for循环对每个样本进行 d w 1 , d w 2 dw1,dw2 dw1,dw2和 d b db db的累加计算最后再求平均数的。在深度学习中,样本数量 m m m通常很大,使用for循环会让神经网络程序运行得很慢。所以,我们应该尽量避免使用for循环操作,而使用矩阵运算,能够大大提高程序运行速度。
向量化(Vectorization)
深度学习算法中,数据量很大,在程序中应该尽量减少使用loop循环语句,而可以使用向量运算来提高程序运行速度。
向量化(Vectorization)就是利用矩阵运算的思想,大大提高运算速度。
-
Vectorizing Logistic Regression
整个训练样本构成的输入矩阵 X X X的维度是 ( n x , m ) (n_x,m) (nx,m),权重矩阵 w w w的维度是 ( n x , 1 ) (n_x,1) (nx,1),b是一个常数值,而整个训练样本构成的输出矩阵 Y Y Y的维度为 ( 1 , m ) (1,m) (1,m)。利用向量化的思想,所有m个样本的线性输出 Z Z Z可以用矩阵表示:

-
Vectorizing Logistic Regression’s Gradient Output
逻辑回归中的梯度下降算法转化为向量化的矩阵形式。对于所有m个样本, d Z dZ dZ的维度是 ( 1 , m ) (1,m) (1,m),可表示为:

d b db db可表示为:

d w dw dw可表示为:
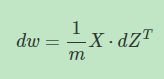
浅层神经网络
神经网络概述(Neural Networks Overview)
神经网络的结构与逻辑回归类似,只是神经网络的层数比逻辑回归多一层,多出来的中间那层称为隐藏层或中间层。这样从计算上来说,神经网络的正向传播和反向传播过程只是比逻辑回归多了一次重复的计算。正向传播过程分成两层,第一层是输入成到隐藏层,用上标[1]来表示:
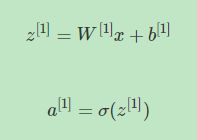
第二层是隐藏层到输出层,用上标[2]来表示:

方括号上标[i]表示当前所处的层数,圆括号上标(i)表示第i个样本。
同样反向传播也分成两层。第一层是输出层到隐藏层,第二层是隐藏层到输入层。
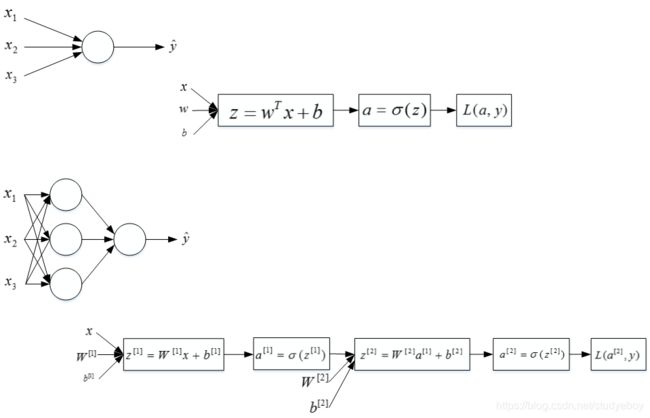
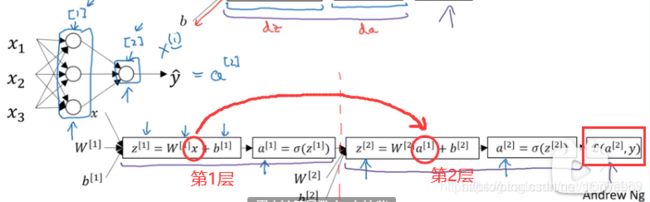
上述的简单网络模型本质上是将逻辑回归重复了两次构成的。
神经网络表示(Neural Network Representation)
下面以图的方式介绍单隐藏层的神经网络结构。如下图所示,单隐藏层神经网络就是典型的浅层(shallow)神经网络。

结构上,从左到右,可分为三层:输入层(Input layer),隐藏层(Hidden layer)和输出层(Output layer)。输入层和输出层,对应训练样本的输入和输出,隐藏层是抽象的非线性的中间层。
写法上,把输入矩阵 X X X记为 a [ 0 ] a^{[0]} a[0],把隐藏层输出记为 a [ 1 ] a^{[1]} a[1],上标从0开始。用下标表示第几个神经元,下标从1开始,例如 a 1 [ 1 ] a^{[1]}_1 a1[1]表示隐藏层第1个神经元。相应的输出层记为 a [ 2 ] a^{[2]} a[2],即 y ^ \hat y y^。这种单隐藏层神经网络也被称为两层神经网络(2 layer NN)。因为,通常只计算隐藏层输出和输出层的输出,输入层是不用计算的。这也是为什么把输入层层数上标记为0的原因。
隐藏层对应的权重 W [ 1 ] W^{[1]} W[1]和常数项 b [ 1 ] b^{[1]} b[1], W [ 1 ] W^{[1]} W[1]的维度是(4,3)。这里的4对应着隐藏层神经元个数,3对应着输入层 X X X特征向量包含元素个数。常数项 b [ 1 ] b^{[1]} b[1]的维度是(4,1),4同样对应着隐藏层神经元个数。关于输出层对应的权重 W [ 2 ] W^{[2]} W[2]和常数项 b [ 2 ] b^{[2]} b[2], W [ 2 ] W^{[2]} W[2]的维度是(1,4),1对应输出层神经元个数,4对应着隐藏层神经元个数。 b [ 2 ] b^{[2]} b[2]的维度是(1,1),因为输出层只有一个神经元。总之,第i层的权重 W [ i ] W^{[i]} W[i]维度的行等于第i层神经元的个数,列等于第i-1层神经元的个数;第i层常数项 b [ i ] b^{[i]} b[i]维度的行等于第i层神经元的的个数,列始终为1.
计算神经网络的输出(Computing a Neural Network’s Output)
两层神经网络可以看成是逻辑回归再重复计算一次。如下图所示,逻辑回归的正向计算可以分解成计算z和a的两部分。
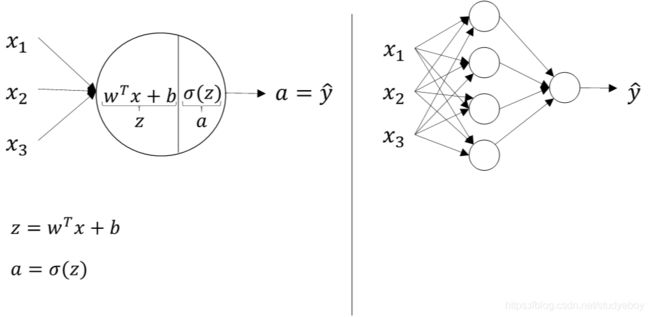
对于两层神经网络,从输入层到隐藏层对应一次逻辑回归运算;从隐藏层到输出层对应一次逻辑回归计算。每层计算时,要注意对应的上标和下标,一般记上标方括号表示layer,下标表示第几个神经元。例如 a i [ l ] a^{[l]}_i ai[l]表示第l层的第i 神经元。注意,i从1开始,l从0开始。
输入层到隐藏层的计算公式:
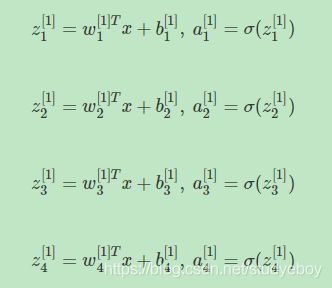
隐藏层到输出层的计算公式:

上述每个节点 的计算都对应着一次逻辑运算的过程,分别由计算z和a两部分组成。
为了提高程序运算速度,引入向量化和矩阵运算的思想,将上述表达式转换成矩阵运算的形式:
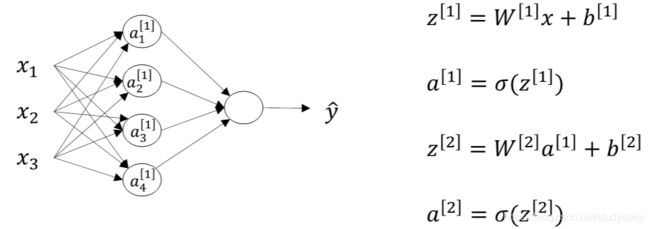
注意: W [ 1 ] W^{[1]} W[1]的维度是(4,3), b [ 1 ] b^{[1]} b[1]的维度是(4,1), W [ 2 ] W^{[2]} W[2]的维度是(1,4), b [ 2 ] b^{[2]} b[2]的维度是(1,1)
多样本向量化(Vectorizing across multiple examples)
上面介绍了单个样本的神经网络正向传播矩阵运算过程。而对于m个训练样本,也可以使用矩阵相乘的形式来提高计算效率。
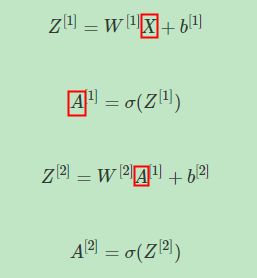
其中输入矩阵 X X X的维度为 ( n x , m ) (n_x, m) (nx,m), Z [ 1 ] Z^{[1]} Z[1]的维度是(4,m),4是隐藏层神经元的个数, A [ 1 ] A^{[1]} A[1]的维度与 Z [ 1 ] Z^{[1]} Z[1]的维度相同, A [ 2 ] A^{[2]} A[2]的维度与 Z [ 2 ] Z^{[2]} Z[2]的维度均为(1,m)。该四个矩阵,均可以这样来理解:行表示神经元个数,列表示样本数目m。
激活函数(Activation functions)
神经网络隐藏层和输出层都需要激活函数(activation function)。不同激活函数形状不同,a的取值范围也有差异。
-
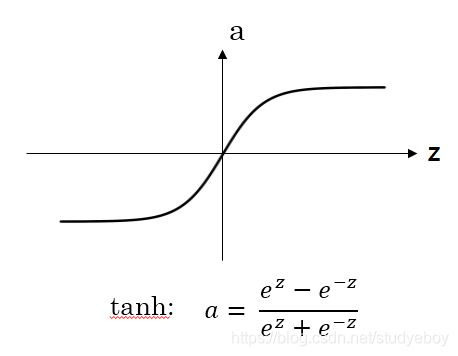
对于隐藏层的激活函数,一般来说tanh函数比sigmoid函数表现更好一些。因为tanh函数的取值范围在[-1,1]之间,隐藏层的输出被限定在[-1,1]之间,可以看成是在0值附近分布,均值为0。这样从隐藏层到输出层,数据起到了归一化(均值为0)的效果。因此,隐藏层的激活函数,tanh比sigmoid更好一些。
-
对于输出层的激活函数,因为二分类问题的输出取值为{0,1},所以一般会选择sigmoid函数作为激活函数。
-
对于sigmoid函数和tanh函数,当|z|很大的时候,激活函数的斜率(梯度)很小,因此,在这个区域内梯度下降算法会运行的比较慢。在实际应用中,应尽量避免使用z落在这个区域,使|z|尽可能限定在零值附近,从而提高梯度下降算法运算速度。
-
ReLU激活函数在z大于零时梯度始终为1,在z小于零时梯度始终为0,z等于零时梯度可以当成1也可以当成0,实际应用中并不影响。对于隐藏层,选择ReLU作激活函数能够保证z大于零时梯度始终为1,从而提高神经网络梯度下降算法运算速度。但当z小于零时,存在梯度为0的缺点,实际应用中,这个缺点影响不是很大。
-
Leaky ReLU激活函数能够保证z小于零是梯度不为0。
-
如果是分类问题,输出层的激活函数一般会选择sigmoid函数。但是隐藏层的激活函数通常不会选择sigmoid函数,tanh函数的表现会比sigmoid函数好一些。实际应用中,通常UI选择使用ReLU或者Leaky ReLU函数,保证梯度下降速度不会太小。其实,具体选择哪个函数作为激活函数没有固定的准确的答案,应该要根据具体实际问题进行验证。
为什么用非线性激活函数(Why do you need non-linear activation functions)
上面的激活函数都是非线性(non-linear)的,是否可以使用线性激活函数?

如果所有隐藏层全部使用线性激活函数,只有输出使用非线性激活函数,那么整个神经网络的结构类似于一个简单的逻辑回归模型,而失去了神经网络模型本身的优势和价值。
如果是预测问题而不是分类问题,输出y是连续的情况下,输出层的激活函数可以使用线性函数。如果输出y恒为正值,则也可以使用ReLU激活函数,具体情况,具体分析。
激活函数的导数(Derivatives of activation functions)
在梯度下降反向计算过程中激活函数的导数和梯度。
神经网络梯度下降(Gradient descent for neural networks)
反向传播(Backpropagation intuition)
使用计算图的方式推导神经网络反向传播过程。由于多了一个隐藏层,神经网络的计算图要比逻辑回归的复杂一些,如下图所示,对于单个训练样本,正向过程很容易,反向过程可以根据梯度计算方法逐一推导。

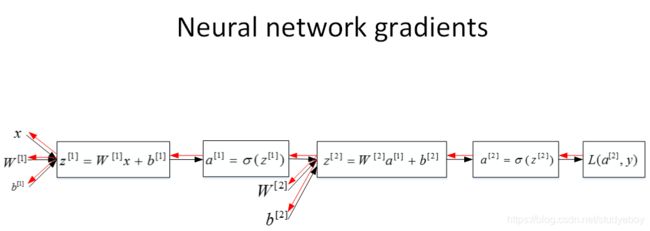
浅层神经网络(包含一个隐藏层),m个训练样本的正向传播过程和反向传播过程分别包含了6个表达式,其向量化矩阵形式如下图所示:

随机初始化(Random Initialization)
神经网络模型中的参数权重 W W W是不能全部初始化为零的。


把这种权重W全部初始化为零带来的问题称为symmetry breaking problem。解决方法就是将W进行随机初始化(b可以初始化为零)。
这里我们将 W 1 [ 1 ] W^{[1]}_1 W1[1]和 W 2 [ 1 ] W^{[1]}_2 W2[1]乘以0.01的目的是尽量使得权重W初始化比较小的值。之所以让W比较小,是因为如果使用sigmoid函数或者tanh函数作为激活函数的话,W比较小,得到的|z|也比较小(靠近零点),而零点区域的梯度比较大,这样能大大提高梯度下降算法的更新速度,尽快找到全局最优解。如果W较大,得到的|z|也比较大,附近曲线平缓,梯度较小,训练过程会慢很多。
当然,如果激活函数是ReLU或者Leaky ReLU函数,则不需要考虑这个问题。但是,如果输出层是sigmoid函数,则对应的权重W最好初始化到比较小的值。
深层神经网络
深层神经网络的符号表示(Deep L-layer neural network)
深层神经玩了个其实就是包含更多的隐藏层神经网络。如下图所示,分别是逻辑回归、1个隐藏层的神经网络、2个隐藏层的神经网络和5个隐藏层的神经网络的模型结构。

命名规则上,一般只参考隐藏层个数和输出层。例如,上图中的逻辑回归又叫1 layer NN,1个隐藏层的神经网络叫做2 layer NN,2个隐藏层的神经网络叫做3 layer NN,以此类推。如果是L-layer NN,则包含了L-1个隐藏层,最后的L层是输出层。
深层神经网络的前向传播(Forward Propagation in a Deep Network)
深层神经网络的正向传播过程,以上面4层神经网络为例,对于单个样本:

如果有m个训练样本,其向量化矩阵形式为:

核对矩阵的维度(Getting your matrix dimensions right)
为什么深层神经网络强大(Why deep representations?)
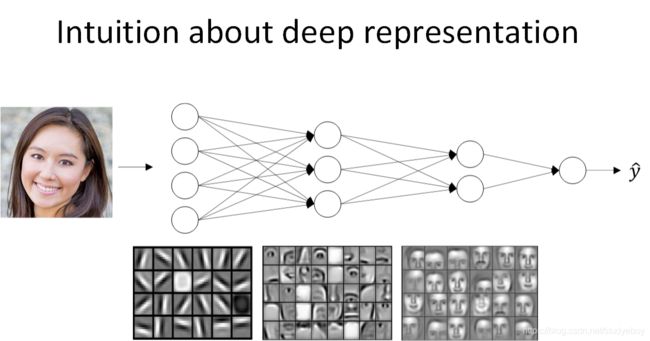
神经网络能处理很多问题,而且效果显著。其强大能力主要源自神经网络足够“深”,也就是说网络层数越多,神经网络就更加复杂和深入,学习也更加准确。
先来看人脸识别的例子,如下图所示。经过训练,神经网络第一层所做的事就是从原始图片中提取出人脸的轮廓与边缘,即边缘检测。这样每个神经元得到的是一些边缘信息。神经网络第二层所做的事情就是将前一层的边缘进行组合,组合成人脸一些局部特征,比如眼睛、鼻子、嘴巴等。再往后面,就将这些局部特征组合起来,融合成人脸的模样。可以看出,随着层数由浅到深,神经网络提取的特征也是从边缘到局部特征到整体,由简单到复杂。可见,如果隐藏层足够多,那么能够提取的特征就越丰富、越复杂,模型的准确率就会越高。


单减深层神经网络块(Building blocks of deep neural networks)

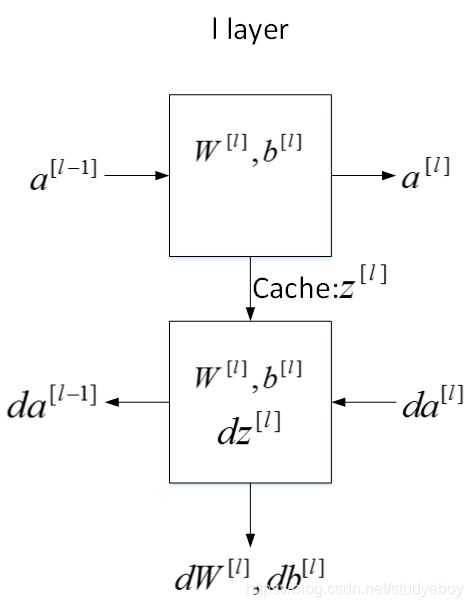
上面是第 l l l层的流程块,对于神经网络所有层,整体流程块图正向传播过程和反向传播过程如下所示:
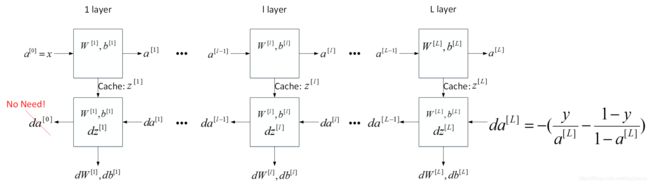
正向传播流程图,在这幅图中标出了各个参数变量以及传播的方向。
- 方框表示神经网络的每一层中的参数
- 蓝色箭头表示前向传播
- 红色箭头表示反向传播
- 绿色箭头表示前向传播的缓存变量值,方便反向传播计算使用
- 紫色箭头表示计算出的供参数更新的导数值

在如上过程中,实现了一次梯度下降的循环。将计算出来的 z , w , b z,w,b z,w,b值进行缓存,在编程时会发现缓存非常方便,因为在计算机反向传播中的导数时,缓存的数据可以迅速提供,从而快速求得 d w , d b dw,db dw,db。
正向传播和反向传播(Forward and Backward Propagation)
参数和超参数(Parameters vs Hyperparameters)
神经网络中的参数就是我们熟悉的 W [ l ] W^{[l]} W[l]和 b [ l ] b^{[l]} b[l]。而超参数则是例如学习速率 α \alpha α,训练迭代次数 N N N,神经网络层数 L L L,各层神经元个数 n [ l ] n^{[l]} n[l],激活函数 g ( z ) g(z) g(z)等。之所以叫做超参数的原因是它们决定了参数 W [ l ] W^{[l]} W[l]和 b [ l ] b^{[l]} b[l]的值。
神经网络和人脑机制的联系(What does this have to do with the brain?)
神经网络实际上可以分成两个部分:正向传播过程和反向传播过程。神经网络的每个神经元采用激活函数的方式,类似于感知机模型。这种模型与人脑神经元是类似的,可以说是一种非常简化的人脑神经元模型。如下图所示,人脑神经元可分为树突、细胞体、轴突三部分。树突接收外界电刺激信号(类比神经网络中神经元输入),传递给细胞体进行处理(类比神经网络中神经元激活函数运算),最后由轴突传递给下一个神经元(类比神经网络中神经元输出)。
优化深度神经网络
深度学习应用
训练集/验证集/测试集(Train/Dev/Test sets)
选择最佳的训练集(Training sets)、验证集(Development sets)、测试集(Test sets)对神经网络的性能影响非常重要。
对于一个需要解决的问题的样本数据,在建立模型的过程中,我们会将问题的data划分为以下几个部分:
- 训练集(train set):用训练集对算法或模型进行训练过程;
- 验证集(development set):利用验证集或者又称为简单交叉验证集(hold-out cross validation set)进行交叉验证,选择出最好的模型;
- 测试集(test set):最后利用测试集对模型进行测试,获取模型运行的无偏估计。
小数据时代
在小数据量的时代,如:100、1000、10000的数据量大小,可以将data做以下划分:
- 无验证集的情况:70% / 30%;
- 有验证集的情况:60% / 20% / 20%;
大数据时代
在如今的大数据时代,对于一个问题,拥有的数据量可能是百万级别的,所以验证集所占的比重会趋向于变得更小。
验证集的目的是为了验证不同的算法哪种更加有效,所以验证集只要足够大能够验证大约2-10种算法哪种算法更好就足够了。
测试的主要目的是评估模型的效果,如在单个分类器中,往往在百万级别的数据中,选择其中1000条数据足以评估单个模型的效果。
- 100万数据量:98% / 1% / 1%;
- 超百万数据量:99.5% / 0.25% / 0.25%(或者99.5% / 0.4% / 0.1%)
注意
- 建议验证集要和训练集来自于同一个分布,可以使得机器学习算法变得更快;
- 如果不需要用无偏估计来评估模型的性能,则可以不需要测试集。
偏差/方差(Bias/Variance)
偏差(Bias)和方差(Variance)是机器学习领域非常重要的两个概念和需要解决的问题。在传统的机器学习算法中,Bias和Variance是对立的,分别对应着欠拟合和过拟合,我们常常需要在Bias和Variance之间进行权衡。而在深度学习中,我们可以同时减小Bias和Variance,构建最佳神经网络模型。
如下图所示,显示了二维平面上,high bias,just right,high variance的例子。可见,high bias对应着欠拟合,而high variance对应着过拟合。

上图这个例子中输入特征是二维的,high bias和high variance可以直接从图中分类线看出来。而对于输入特征是高维的情况,可以通过两个数值Train set error和Dev set error来理解bias和variance。
- 假设Train set error为1%,而Dev set error为11%,即该算法模型对训练样本的识别很好,但是对验证集的识别却不太好。这说明了该模型对训练样本可能存在过拟合,模型泛化能力不强,导致验证集识别率低。这恰恰是high variance的表现。
- 假设Train set error为15%,而Dev set error为16%,虽然二者error接近,即该算法模型对训练样本和验证集的识别都不是太好。这说明了该模型对训练样本存在欠拟合。这恰恰是high bias的表现。
- 假设Train set error为15%,而Dev set error为30%,说明了该模型既存在high bias也存在high variance(深度学习中最坏的情况)。
- 再假设Train set error为0.5%,而Dev set error为1%,即low bias和low variance,是最好的情况。


以上的这些假设都是建立在base error是0的基础上,base error不同,相应的Train set error和Dev set error会有所变化,但没有相对变化。
一般来说,Train set error体现了是否出现bias,Dev set error体现了是否出现variance(正确地说,应该是Dev set error与Train set error的相对差值)。
下图展示了high bias and high variance的模型,模型既存在high bias也存在high variance,可以理解成某段区域是欠拟合的,某段区域是过拟合的。
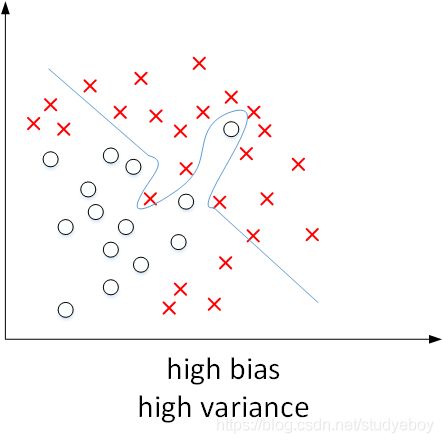
机器学习的基本方法(Basic Recipe for Machine Learning)
解决high bias和high variance的方法是不同的。实际应用中通过Train set error和Dev set error判断是否出现了high bias或者high variance,然后再选择针对性的方法解决问题。
传统机器学习算法中,Bias和Variance通常是对立的,减小Bias会增加Variance,减小Variance会增加Bias。而在现在的深度学习中,通过使用更复杂的神经网络和海量的训练样本,一般能够同时有效减小Bias和Variance。
解决high bias方法:
- 增加网络结构,如增加隐藏层数目;
- 训练更长时间;
- 寻找合适的网络架构,使用更大的NN结构;
解决high variance方法:
- 获取更多的数据;
- 正则化( regularization);
- 寻找合适的网络结构;
正则化(Regularization)
如果出现了过拟合,即high variance,则需要采用正则化regularization来解决。虽然扩大训练样本数量也是减小high variance的一种方法,但是通常获得更多训练样本的成本太高,比较困难。所以,更可行有效的办法就是使用regularization。
逻辑回归(Logistic regression)中的正则化

注意
- 为什么只对w进行正则化而不对b进行正则化呢?其实也可以对b进行正则化。但是一般w的维度很大,而b只是一个常数。相比较来说,参数很大程度上由w决定,改变b值对整体模型影响较小。所以,一般为了简便,就忽略对b的正则化了。
- 与L2 regularization相比,L1 regularization得到的w更加稀疏,即很多w为零值。其优点是节约存储空间,因为大部分w为0。然而,实际上L1 regularization在解决high variance方面比L2 regularization并不更具优势。而且,L1的在微分求导方面比较复杂。所以,一般L2 regularization更加常用。
- L1、L2 regularization中的λλ就是正则化参数(超参数的一种)。可以设置λ为不同的值,在Dev set中进行验证,选择最佳的λ。
- 在python中,由于lambda是保留字,所以为了避免冲突,我们使用lambd来表示λ。
为什么正则化可以减小过拟合(Why regularization reduces overfitting)
直观理解
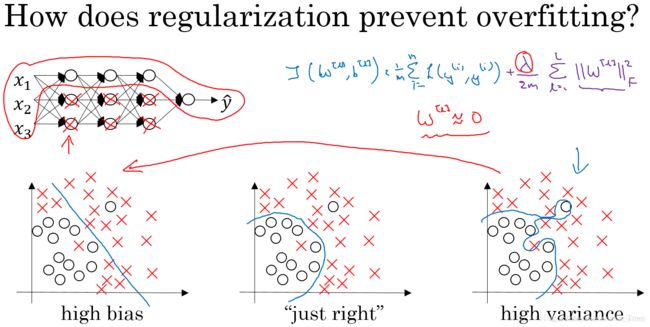
假如我们选择了非常复杂的神经网络模型,如上图左上角所示。在未使用正则化的情况下,我们得到的分类超平面可能是类似上图右侧的过拟合。但是,如果使用L2 regularization,当 λ λ λ很大时, w [ l ] ≈ 0 w^{[l]}≈0 w[l]≈0。 w [ l ] w^{[l]} w[l]近似为零,意味着该神经网络模型中的某些神经元实际的作用很小,可以忽略。从效果上来看,其实是将某些神经元给忽略掉了。这样原本过于复杂的神经网络模型就变得不那么复杂了,而变得非常简单化了。如下图所示,整个简化的神经网络模型变成了一个逻辑回归模型。问题就从high variance变成了high bias了。因此,选择合适大小的 λ λ λ值,就能够同时避免high bias和high variance,得到最佳模型。
数学解释
tanh函数的特点是在 z z z接近零的区域,函数近似是线性的,而当 ∣ z ∣ |z| ∣z∣很大的时候,函数非线性且变化缓慢。当使用正则化,当 λ λ λ增大,即对权重 w [ l ] w^{[l]} w[l]的惩罚较大, w [ l ] w^{[l]} w[l]减小。因为 z [ l ] = w [ l ] a [ l ] + b [ l ] z^{[l]}=w^{[l]}a^{[l]}+b^{[l]} z[l]=w[l]a[l]+b[l]。当 w [ l ] w^{[l]} w[l]减小的时候, z [ l ] z^{[l]} z[l]也会减小。则此时的 z [ l ] z^{[l]} z[l]分布在tanh函数的近似线性区域。那么这个神经元起的作用就相当于是linear regression。如果每个神经元对应的权重 w [ l ] w^{[l]} w[l]都比较小,那么整个神经网络模型相当于是多个linear regression的组合,即可看成一个linear network。得到的分类超平面就会比较简单,不会出现过拟合现象。

Dropout 正则化(Dropout Regularization)
Dropout是指在深度学习网络的训练过程中,对于每层的神经元,按照一定的概率将其暂时从网络中丢弃。也就是说,每次训练时,每一层都有部分神经元不工作,起到简化复杂网络模型的效果,从而避免发生过拟合。

Dropout有不同的实现方法,反向随机失活(Inverted dropout)是常用的方法。

理解 Dropout
从权重w的角度来解释为什么dropout能够有效防止过拟合。对于某个神经元来说,某次训练时,它的某些输入在dropout的作用被过滤了。而在下一次训练时,又有不同的某些输入被过滤。经过多次训练后,某些输入被过滤,某些输入被保留。这样,该神经元就不会受某个输入非常大的影响,影响被均匀化了。也就是说,对应的权重w不会很大。这从从效果上来说,与L2 regularization是类似的,都是对权重w进行“惩罚”,减小了w的值。

对于同一组训练数据,利用不同的神经网络训练之后,求其输出的平均值可以减少overfitting。Dropout就是利用这个原理,每次丢掉一定数量的隐藏层神经元,相当于在不同的神经网络上进行训练,这样就减少了神经元之间的依赖性,即每个神经元不能依赖于某几个其他的神经元(指层与层之间相连接的神经元),使神经网络更加能学习到与其他神经元之间的更加健壮robust的特征。
注意
- 不同隐藏层的dropout系数keep_prob可以不同。一般来说,神经元越多的隐藏层,keep_out可以设置得小一些;神经元越少的隐藏层,keep_out可以设置的大一些。
- 实际应用中,不建议对输入层进行dropout。
- dropout是一种regularization技巧,用来防止过拟合的,最好只在需要regularization的时候使用dropout。
- dropout的一大缺点就是其使得 Cost function不能再被明确的定义,以为每次迭代都会随机消除一些神经元结点,所以我们无法绘制出每次迭代 J ( W , b ) J(W,b) J(W,b)下降的图。
Dropout使用
- 关闭dropout功能,即设置 keep_prob = 1.0;
- 运行代码,确保 J ( W , b ) J(W,b) J(W,b)函数单调递减;
- 再打开dropout函数。
其他正则化方法(Other regularization methods)
数据增强
一种方法是增加训练样本数量。但是通常成本较高,难以获得额外的训练样本。但是,我们可以对已有的训练样本进行一些处理来“制造”出更多的样本,称为data augmentation。例如图片识别问题中,可以对已有的图片进行水平翻转、垂直翻转、任意角度旋转、缩放或扩大等等。如下图所示,这些处理都能“制造”出新的训练样本。虽然这些是基于原有样本的,但是对增大训练样本数量还是有很有帮助的,不需要增加额外成本,却能起到防止过拟合的效果。
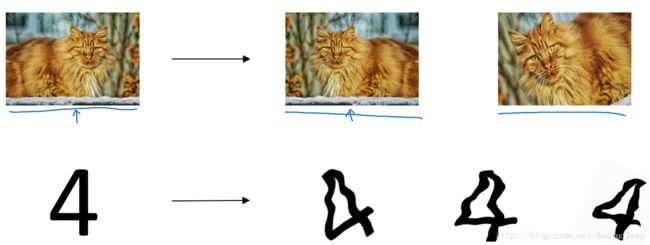
early stopping
一个神经网络模型随着迭代训练次数增加,train set error一般是单调减小的,而dev set error 先减小,之后又增大。也就是说训练次数过多时,模型会对训练样本拟合的越来越好,但是对验证集拟合效果逐渐变差,即发生了过拟合。因此,迭代训练次数不是越多越好,可以通过train set error和dev set error随着迭代次数的变化趋势,选择合适的迭代次数,即early stopping。

Early stopping有其自身缺点。通常来说,机器学习训练模型有两个目标:一是优化cost function,尽量减小J;二是防止过拟合。这两个目标彼此对立的,即减小J的同时可能会造成过拟合,反之亦然。我们把这二者之间的关系称为正交化orthogonalization。在深度学习中,我们可以同时减小Bias和Variance,构建最佳神经网络模型。但是,Early stopping的做法通过减少待训练次数来防止过拟合,这样J就不会足够小。也就是说,early stopping将上述两个目标融合在一起,同时优化,但可能没有“分而治之”的效果好。
与early stopping相比,L2 regularization可以实现“分而治之”的效果:迭代训练足够多,减小J,而且也能有效防止过拟合。而L2 regularization的缺点之一是最优的正则化参数λ的选择比较复杂。对这一点来说,early stopping比较简单。总的来说,L2 regularization更加常用一些。
归一化输入(Normalizing inputs)
在训练神经网络时,标准化输入可以提高训练的速度。标准化输入就是对训练数据集进行归一化的操作,即将原始数据减去其均值 μ μ μ后,再除以其方差 σ 2 σ^2 σ2。


由于训练集进行了标准化处理,那么对于测试集或在实际应用时,应该使用同样的 μ μ μ和 σ 2 σ^2 σ2对其进行标准化处理。这样保证了训练集合测试集的标准化操作一致。
对输入进行标准化操作,主要是为了让所有输入归一化同样的尺度上,方便进行梯度下降算法时能够更快更准确地找到全局最优解。假如输入特征是二维的,且 x 1 x_1 x1的范围是[1,1000], x 2 x_2 x2的范围是[0,1]。如果不进行标准化处理, x 1 x_1 x1与 x 2 x_2 x2之间分布极不平衡,训练得到的 w 1 w_1 w1和 w 2 w_2 w2也会在数量级上差别很大。这样导致的结果是cost function与 w w w和 b b b的关系可能是一个非常细长的椭圆形碗。对其进行梯度下降算法时,由于 w 1 w_1 w1和 w 2 w_2 w2数值差异很大,只能选择很小的学习因子 α α α,来避免 J J J发生振荡。一旦 α α α较大,必然发生振荡, J J J不再单调下降。如下左图所示。
然而,如果进行了标准化操作, x 1 x_1 x1与 x 2 x_2 x2分布均匀, w 1 w_1 w1和 w 2 w_2 w2数值差别不大,得到的cost function与 w w w和 b b b的关系是类似圆形碗。对其进行梯度下降算法时, α α α可以选择相对大一些,且 J J J一般不会发生振荡,保证了 J J J是单调下降的。如下右图所示。
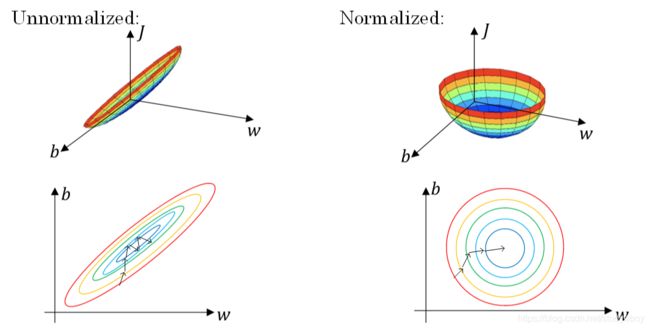
由图可以看出不使用归一化和使用归一化前后Cost function 的函数形状会有很大的区别。
在不使用归一化的代价函数中,如果我们设置一个较小的学习率,那么很可能我们需要很多次迭代才能到达代价函数全局最优解;如果使用了归一化,那么无论从哪个位置开始迭代,我们都能以相对很少的迭代次数找到全局最优解。
梯度消失与梯度爆炸(Vanishing and Exploding gradients)
深度神经网络中存在可能存在这样一个问题:梯度消失和梯度爆炸。意思是当训练一个 层数非常多的神经网络时,计算得到的梯度可能非常小或非常大,甚至是指数级别的减小或增大。这样会让训练过程变得非常困难。
假设一个多层的每层只包含两个神经元的深度神经网络模型,如下图所示:


利用初始化缓解梯度消失和爆炸问题(Weight Initialization for Deep Networks)
改善Vanishing and Exploding gradients这类问题,方法是对权重w进行一些初始化处理。
深度神经网络模型中,以单个神经元为例,该层 ( l ) (l) (l)的输入个数为n,其输出为:

这里忽略了常数项 b b b。为了让 z z z不会过大或者过小,思路是让 w w w与 n n n有关,且 n n n越大, w w w应该越小才好。这样能够保证 z z z不会过大。一种方法是在初始化 w w w时,令其方差为 1 n \frac {1}{n} n1。
可以根据不同的激活函数选择不同方法。另外,我们可以对这些初始化方法中设置某些参数,作为超参数,通过验证集进行验证,得到最优参数,来优化神经网络。
不同激活函数的 Xavier initialization:
- 激活函数使用Relu: V a r ( w i ) = 2 n Var(w_i) = \dfrac{2}{n} Var(wi)=n2
- 激活函数使用tanh: V a r ( w i ) = 1 n Var(w_i) = \dfrac{1}{n} Var(wi)=n1
- Yoshua Bengio提出了另外一种初始化w的方法: V a r ( w i ) = 2 n [ l − 1 ] n [ l ] Var(w_i) = \dfrac{2}{n^{[l-1]}n^{[l]}} Var(wi)=n[l−1]n[l]2
其中 n n n是输入的神经元个数,也就是 n [ l − 1 ] n^{[ l − 1 ]} n[l−1]。
梯度的数值逼近(Numerical approximation of gradients)
Back Propagation神经网络有一项重要的测试是梯度检查(gradient checking)。其目的是检查验证反向传播过程中梯度下降算法是否正确。
使用双边误差的方法去逼近导数:

由图可以看出,双边误差逼近的误差是0.0001,先比单边逼近的误差0.03,其精度要高了很多。
梯度检验(Gradient checking)
近似求出梯度值后,如何进行梯度检查,来验证训练过程中是否出现bugs。

在进行梯度检查的过程中需要注意的地方:
- 不要在整个训练过程中都进行梯度检查,仅仅作为debug使用。
- 如果梯度检查出现错误,找到对应出错的梯度,检查其推导是否出现错误。
- 注意不要忽略正则化项,计算近似梯度的时候要包括进去。
- 梯度检查时关闭dropout,检查完毕后再打开dropout。
- 随机初始化时运行梯度检查,经过一些训练后再进行梯度检查(不常用)。
优化算法
Mini-batch 梯度下降法(Mini-batch gradient descent)
神经网络训练过程是对所有m个样本,称为batch,通过向量化计算方式,同时进行的。如果m很大,例如达到百万数量级,训练速度往往会很慢,因为每次迭代都要对所有样本进行进行求和运算和矩阵运算。我们将这种梯度下降算法称为Batch Gradient Descent。
为了解决这一问题,我们可以把m个训练样本分成若干个子集,称为mini-batches,这样每个子集包含的数据量就小了,例如只有1000,然后每次在单一子集上进行神经网络训练,速度就会大大提高。这种梯度下降算法叫做Mini-batch Gradient Descent。

普通的batch梯度下降法和Mini-batch梯度下降法代价函数的变化趋势,如下图所示:

对于一般的神经网络模型,使用Batch gradient descent,随着迭代次数增加,cost是不断减小的。然而,使用Mini-batch gradient descent,随着在不同的mini-batch上迭代训练,其cost不是单调下降,而是受类似noise的影响,出现振荡。但整体的趋势是下降的,最终也能得到较低的cost值。


比较Batch gradient descent、Stachastic gradient descent和mini-batch gradient descent的梯度下降曲线。
- 蓝色的线代表Batch gradient descent,Batch gradient descent会比较平稳地接近全局最小值,但是因为使用了所有m个样本,每次前进的速度有些慢。如果总体样本数量m不太大时,例如m≤2000,建议直接使用Batch gradient descent。
- 紫色的线代表Stachastic gradient descent,Stachastic gradient descent每次前进速度很快,但是路线曲折,有较大的振荡,最终会在最小值附近来回波动,难以真正达到最小值处。而且在数值处理上就不能使用向量化的方法来提高运算速度。
- 绿色的线代表Mini-batch gradient descent,Mini-batch gradient descent的mini-batch size 不能设置的太大(Batch gradient descent),也不能设置的太小(Stachastic gradient descent)。相当于结合了Batch gradient descent和Stachastic gradient descent各自的优点,既能使用向量化优化算法,又能叫快速地找到最小值。每次前进速度较快,且振荡较小,基本能接近全局最小值。如果总体样本数量m很大时,建议将样本分成许多mini-batches。
指数加权平均(Exponentially weighted averages)
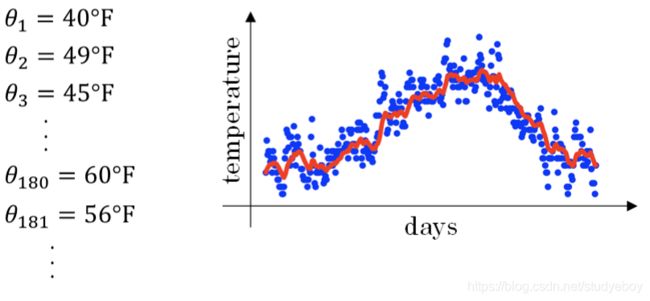
举个例子,记录半年内伦敦市的气温变化,并在二维平面上绘制出来,如下图所示:

看上去,温度数据似乎有noise,而且抖动较大。如果我们希望看到半年内气温的整体变化趋势,可以通过移动平均(moving average)的方法来对每天气温进行平滑处理。

经过移动平均处理得到的气温如下图红色曲线所示:

![]()

指数加权平均的偏差修正(Bias correction in exponentially weighted average)
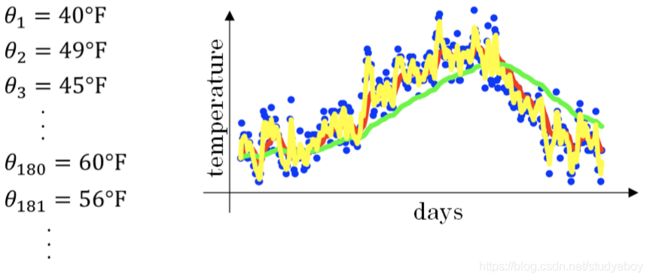
上文中提到当β=0.98时,指数加权平均结果如下图绿色曲线所示。但是实际上,真实曲线如紫色曲线所示。


动量梯度下降法(Gradient descent with momentum)
动量梯度下降算法,其速度要比传统的梯度下降算法快很多。做法是在每次训练时,对梯度进行指数加权平均处理,然后用得到的梯度值更新权重W和常数项b。

原始的梯度下降算法如上图蓝色折线所示。在梯度下降过程中,梯度下降的振荡较大,尤其对于W、b之间数值范围差别较大的情况。此时每一点处的梯度只与当前方向有关,产生类似折线的效果,前进缓慢。而如果对梯度进行指数加权平均,这样使当前梯度不仅与当前方向有关,还与之前的方向有关,这样处理让梯度前进方向更加平滑,减少振荡,能够更快地到达最小值处。
RMSprop
RMSprop是另外一种优化梯度下降速度的算法。每次迭代训练过程中,其权重W和常数项b的更新表达式为:
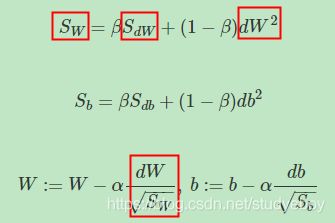
下面简单解释一下RMSprop算法的原理,仍然以下图为例,为了便于分析,令水平方向为W的方向,垂直方向为b的方向。


Adam 优化算法(Adam optimization algorithm)
Adam(Adaptive Moment Estimation)算法结合了动量梯度下降算法和RMSprop算法。实际应用中,Adam算法结合了动量梯度下降和RMSprop各自的优点,使得神经网络训练速度大大提高。其算法流程为:

学习率衰减(Learning rate decay)
减小学习因子α也能有效提高神经网络训练速度,这种方法被称为learning rate decay。
Learning rate decay就是随着迭代次数增加,学习因子 α α α逐渐减小。下图中,蓝色折线表示使用恒定的学习因子 α α α,由于每次训练 α α α相同,步进长度不变,在接近最优值处的振荡也大,在最优值附近较大范围内振荡,与最优值距离就比较远。绿色折线表示使用不断减小的 α α α,随着训练次数增加, α α α逐渐减小,步进长度减小,使得能够在最优值处较小范围内微弱振荡,不断逼近最优值。相比较恒定的 α α α来说,learning rate decay更接近最优值。

Learning rate decay中对 α α α可由下列公式得到:

局部最优问题(The problem of local optima)
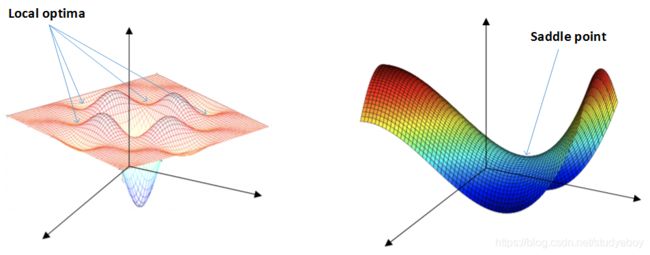
在使用梯度下降算法不断减小cost function时,可能会得到局部最优解(local optima)而不是全局最优解(global optima)。之前我们对局部最优解的理解是形如碗状的凹槽,如下图左边所示。但是在神经网络中,local optima的概念发生了变化。准确地来说,大部分梯度为零的“最优点”并不是这些凹槽处,而是形如右边所示的马鞍状,称为saddle point。也就是说,梯度为零并不能保证都是convex(极小值),也有可能是concave(极大值)。特别是在神经网络中参数很多的情况下,所有参数梯度为零的点很可能都是右边所示的马鞍状的saddle point,而不是左边那样的local optimum。
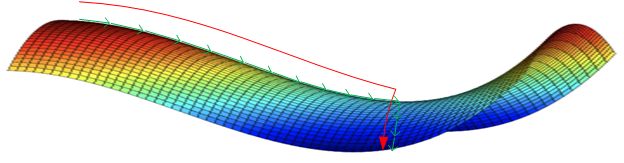
类似马鞍状的plateaus会降低神经网络学习速度。Plateaus是梯度接近于零的平缓区域,如下图所示。在plateaus上梯度很小,前进缓慢,到达saddle point需要很长时间。到达saddle point后,由于随机扰动,梯度一般能够沿着图中绿色箭头,离开saddle point,继续前进,只是在plateaus上花费了太多时间。
关于local optima和plateaus:
- 只要选择合理的强大的神经网络,一般不太可能陷入local optima
- Plateaus可能会使梯度下降变慢,降低学习速度,动量梯度下降,RMSprop,Adam算法都能有效解决plateaus下降过慢的问题,大大提高神经网络的学习速度。
超参数调试、Batch正则化
超参数调试(Tuning Process)
深度神经网络需要调试的超参数(Hyperparameters)较多,包括:
![]()
超参数之间也有重要性差异。通常来说,学习因子 α α α是最重要的超参数,也是需要重点调试的超参数。动量梯度下降因子 β β β、各隐藏层神经元个数#hidden units和mini-batch size的重要性仅次于 α α α。然后就是神经网络层数#layers和学习因子下降参数learning rate decay。最后,Adam算法的三个参数 β 1 , β 2 , ε β1,β2,ε β1,β2,ε一般常设置为0.9,0.999和10−8,不需要反复调试。当然,这里超参数重要性的排名并不是绝对的,具体情况,具体分析。
如何选择和调试超参数?传统的机器学习中,我们对每个参数等距离选取任意个数的点,然后,分别使用不同点对应的参数组合进行训练,最后根据验证集上的表现好坏,来选定最佳的参数。例如有两个待调试的参数,分别在每个参数上选取5个点,这样构成了5x5=25中参数组合,如下图所示:
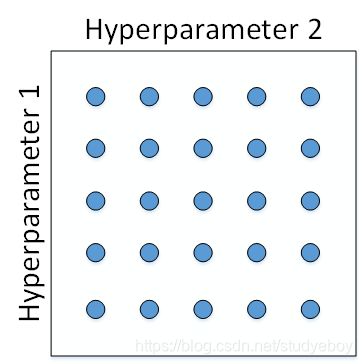
这种做法在参数比较少的时候效果较好。但是在深度神经网络模型中,我们一般不采用这种均匀间隔取点的方法,比较好的做法是使用随机选择。随机化选择参数的目的是为了尽可能地得到更多种参数组合。对于上面这个例子,我们随机选择25个点,作为待调试的超参数,如下图所示:

这种做法带来的另外一个好处就是对重要性不同的参数之间的选择效果更好。假设hyperparameter1为 α α α,hyperparameter2为 ε ε ε,显然二者的重要性是不一样的。如果使用第一种均匀采样的方法, ε ε ε的影响很小,相当于只选择了5个 α α α值。而如果使用第二种随机采样的方法, ε ε ε和 α α α都有可能选择25种不同值。这大大增加了 α α α调试的个数,更有可能选择到最优值。其实,在实际应用中完全不知道哪个参数更加重要的情况下,随机采样的方式能有效解决这一问题,但是均匀采样做不到这点。
在经过随机采样之后,我们可能得到某些区域模型的表现较好。然而,为了得到更精确的最佳参数,我们应该继续对选定的区域进行由粗到细的采样(coarse to fine sampling scheme)。也就是放大表现较好的区域,再对此区域做更密集的随机采样。例如,对下图中右下角的方形区域再做25点的随机采样,以获得最佳参数。
![]()
为超参数选择合适的范围(Using an appropriate scale to pick hyperparameters)
上面说的调试参数使用随机采样,对于某些超参数是可以进行尺度均匀采样的,但是某些超参数需要选择不同的合适尺度进行随机采样。
例如对于超参数#layers和#hidden units,都是正整数,是可以进行均匀随机采样的,即超参数每次变化的尺度都是一致的(如每次变化为1,犹如一个刻度尺一样,刻度是均匀的)。
但是,对于某些超参数,可能需要非均匀随机采样(即非均匀刻度尺)。例如超参数 α α α,待调范围是[0.0001, 1]。如果使用均匀随机采样,那么有90%的采样点分布在[0.1, 1]之间,只有10%分布在[0.0001, 0.1]之间。这在实际应用中是不太好的,因为最佳的 α α α值可能主要分布在[0.0001, 0.1]之间,而[0.1, 1]范围内 α α α值效果并不好。因此我们更关注的是区间[0.0001, 0.1],应该在这个区间内细分更多刻度。
通常的做法是将linear scale转换为log scale,将均匀尺度转化为非均匀尺度,然后再在log scale下进行均匀采样。这样,[0.0001, 0.001],[0.001, 0.01],[0.01, 0.1],[0.1, 1]各个区间内随机采样的超参数个数基本一致,也就扩大了之前[0.0001, 0.1]区间内采样值个数。


超参数调试实践–Pandas vs. Caviar(Hyperparameters tuning in practice: Pandas vs. Caviar)
经过调试选择完最佳的超参数并不是一成不变的,一段时间之后(例如一个月),需要根据新的数据和实际情况,再次调试超参数,以获得实时的最佳模型。
在训练深度神经网络时,一种情况是受计算能力所限,我们只能对一个模型进行训练,调试不同的超参数,使得这个模型有最佳的表现。我们称之为Babysitting one model。另外一种情况是可以对多个模型同时进行训练,每个模型上调试不同的超参数,根据表现情况,选择最佳的模型。我们称之为Training many models in parallel。

因为第一种情况只使用一个模型,所以类比做Panda approach;第二种情况同时训练多个模型,类比做Caviar approach。使用哪种模型是由计算资源、计算能力所决定的。一般来说,对于非常复杂或者数据量很大的模型,使用Panda approach更多一些。
- 在计算资源有限的情况下,使用第一种,仅调试一个模型,每天不断优化;
- 在计算资源充足的情况下,使用第二种,同时并行调试多个模型,选取其中最好的模型。
网络中激活值的归一化(Normalizing activations in a network)
在训练神经网络时,标准化输入可以提高训练的速度。方法是对训练数据集进行归一化的操作,即将原始数据减去其均值 μ μ μ后,再除以其方差 σ 2 σ^2 σ2。但是标准化输入只是对输入进行了处理,那么对于神经网络,又该如何对各隐藏层的输入进行标准化处理呢?


Batch Norm应用到神经网络(Fitting Batch Norm into a neural network)
已经知道了如何对单一隐藏层的所有神经元进行Batch Norm,接下来将Batch Norm应用到整个神经网络中。
对L层神经网络,经过Batch Norm的作用,整体流程如下:
![]()

Batch Norm起作用的原因(Why does Batch Norm work?)
输入归一化把输入特征做均值为0,方差为1的规范化处理,来加快学习速度。而Batch Norm也对隐藏层个神经元的输入做类似的规范化处理。总的来说,Batch Norm不仅能够提高神经网络训练速度,而且能让神经网络的权重W的更新更加“稳健”,尤其在深层神经网络中更加明显。比如神经网络很后面的W对前面的W包容性更强,即前面的W的变化对后面W造成的影响很小,整体网络更加健壮。
假如用一个浅层神经网络(类似逻辑回归)来训练识别猫的模型,如下图所示,提供的所有猫的训练样本都是黑猫。然后,用这个训练得到的模型来对各种颜色的猫样本进行测试,测试的结果可能并不好。其原因是训练样本不具有一般性(即不是所有的猫都是黑猫),这种训练样本(黑猫)和测试样本(猫)分布的变化称为Covariate shift。

对于这种情况,如果实际应用的样本与训练样本分布不同,即发生了Covariate shift,则一般是要对模型重新进行训练的。在神经网络尤其是深度神经网络中,Covariate shift会导致模型预测效果变差,重新训练的模型个隐藏层的 W [ l ] W^{[l]} W[l]和 B [ l ] B^{[l]} B[l]均产生偏移、变化。而Batch Norm的作用恰恰是减小Covariate shift的影响,让模型变得更加健壮,鲁棒性更强。Batch Norm减少了各层 W [ l ] W^{[l]} W[l]和 B [ l ] B^{[l]} B[l]之间的耦合性,让各层更加独立,实现自我训练学习的效果。也就是说,如果输入发生了Covariate shift,那么因为Batch Norm的作用,对这个隐藏层输出 Z [ l ] Z^{[l]} Z[l]进行均值和方差的归一化处理, W [ l ] W^{[l]} W[l]和 B [ l ] B^{[l]} B[l]更加稳定,使得原来的模型也有不错的表现。
考虑在深层神经网络中,遮住前面几层。


遮住前面2层后,这组 a a a作为第3层的输入值,同时这组值由前两层运算而来,每一轮训练会有不同的值,即有不同的这组 a a a值,那么就出现了上述提及的输入值偏移问题。正是因为有这样的问题,所以用Batch Norm可以尽可能使每一层保持相对独立,神经网络的之后层就有更高的稳定性,也有助于神经网络加速学习。但是,Batch Norm处理后,数据方差和均值实际上是被控制住的。
从另一个方面来说,Batch Norm也起到了轻微的正则化(regularization)效果。具体表现在:
- 每个mini-batch都进行均值为0,方差为1的归一化操作
- 每个mini-batch中,对各个隐藏层的 z [ l ] z^{[l]} z[l]添加了随机噪声,效果类似于Dropout
- mini-batch越小,正则化效果越明显
- 但是,Batch Norm的正则化效果比较微弱,正则化也不是Batch Norm的主要功能
测试数据集上使用Batch Norm(Batch Norm at test time)
训练过程中,Batch Norm是对单个mini-batch进行操作的,但在测试过程中,如果是单个样本,该如何使用Batch Norm进行处理?

softmax 回归(Softmax Regression)
逻辑回归对数据进行二分类,用非0即1来判别一幅图像是否是某一物体。如果有多个类别进行分类需要用softmax来处理,Softmax回归也可以看作是逻辑回归的一种一般形式。
给定图像及对应的标签,类别数量一共是C=4。

在逻辑回归的基础上,输出层的单元数调整为C=4。
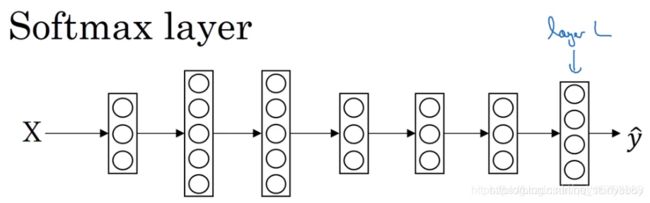
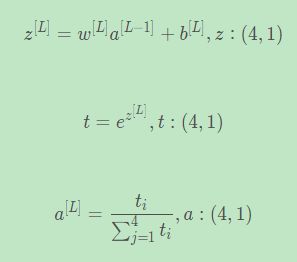
Softmax的激活函数输入值为(4,1)的向量,输出的(4, 1)向量对应四种类别的概率值。
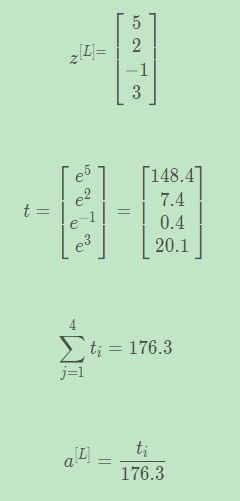

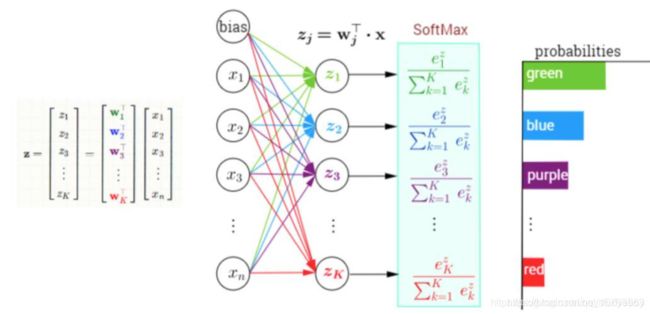
几个简单的线性多分类的例子:

在没有隐藏层的情况下,图像分类的结果是线性的,Softmax回归有决策边界,Softmax回归有两个以上的分类,Softmax回归是逻辑回归的一般形式,将二分类扩展到C分类。
如果加入隐藏层,就可以做非线性分类,即决策边界是曲线。
C=2时,Softmax就是逻辑回归的证明:
C=2时输出为(2,1)矩阵,仅仅需要将这两个值进行偏移(大于0.5取1,小于0.5取0),即实现了0/1的二分类。
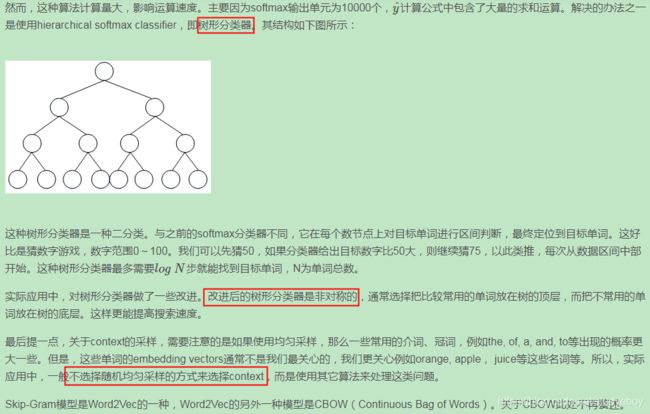
训练softmax分类器(Training a softmax classifier)
对比Hardmax,Hardmax将最大值1放在对应矩阵位置上,其他位置全部置0.而Softmax计算出每种分类的概率,并且概率之和等于1。



构建机器学习项目
机器学习策略(上)
当我们最初得到一个深度神经网络模型时,可能希望从很多方面来对它进行优化,可选择的方法很多,也很复杂、繁琐。盲目选择、尝试不仅耗费时间而且可能收效甚微。因此,使用快速、有效的策略来优化机器学习模型是非常有必要的。
正交化(Orthogonalization)
机器学习中有许多参数、超参数需要调试。通过每次只调试一个参数,保持其它参数不变,而得到的模型某一性能改变是一种最常用的调参策略,我们称之为正交化方法(Orthogonalizatiion)。
Orthogonalization的核心在于每次调试一个参数只会影响模型的某一个性能。这种方法能够让我们更快更有效的进行机器学习模型的调试和优化。
在机器学习监督式学习模型中,以下4个假设需要真实且是相互正交的:
- 系统在训练集上表现好(Fit training set well on cost function)
否则,优化训练集可以通过使用更大更复杂的神经网络,使用Adam等优化算法来实现。 - 系统在开发集(验证集)上表现好(Fit dev set well on cost function)
否则,优化验证集可以通过使用正则化、采用更多训练样本来实现。 - 系统在测试集上表现好(Fit test set well on cost function)
否则,优化测试可以通过使用更多的验证集样本来实现。 - 系统在真实环境中表现好(Performs well in real world)
否则,提升实际应用模型可以通过更换验证集,使用新的cost function来实现。
early stopping在模型功能调试中并不推荐使用。因为early stopping在提升验证集性能的同时降低了训练集的性能。即early stopping同时影响两个功能,不具有独立性、正交性。
单一数字评估指标(Single number evaluation metric)
构建、优化机器学习模型时,单值评价指标非常必要。有了量化的单值评价指标后,我们就能根据这一指标比较不同超参数对应的模型的优劣,从而选择最优的那个模型。
举个例子,比如有A和B两个模型,它们的准确率(Precision)和召回率(Recall)分别如下:
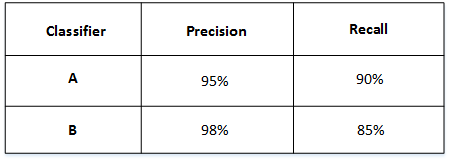
如果只看Precision的话,B模型更好。如果只看Recall的话,A模型更好。实际应用中,我们通常使用单值评价指标F1 Score来评价模型的好坏。F1 Score综合了Precision和Recall的大小。
在二分类问题中,通过预测得到下面的真实值 y y y和预测值 y ^ \hat y y^的表:
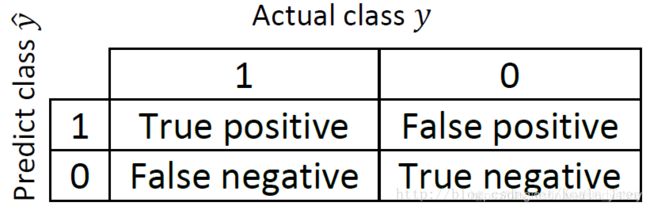
指标的计算方法如下所示:
然后得到了A和B模型各自的F1 Score:
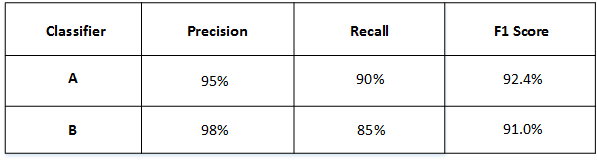
从F1 Score来看,A模型比B模型更好一些。通过引入单值评价指标F1 Score,很方便对不同模型进行比较。
除了F1 Score之外,我们还可以使用平均值作为单值评价指标来对模型进行评估。如下图所示,A, B, C, D, E, F六个模型对不同国家样本的错误率不同,可以计算其平均性能,然后选择平均错误率最小的那个模型(C模型)。
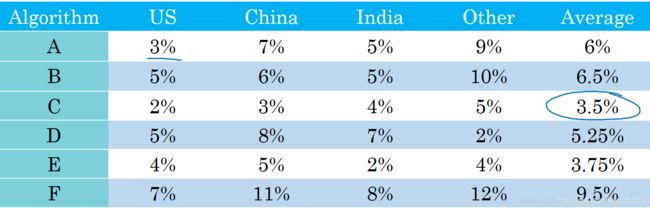
满足和优化指标(Satisficing and Optimizing metic)
有时候,要把所有的性能指标都综合在一起,构成单值评价指标是比较困难的。解决办法是,我们可以把某些性能作为优化指标(Optimizing metic),寻求最优化值;而某些性能作为满意指标(Satisficing metic),只要满足阈值就行了。
性能指标(Optimizing metic)是需要优化的,越优越好;而满意指标(Satisficing metic)只要满足设定的阈值就好了。
举个猫类识别的例子,有A,B,C三个模型,各个模型的Accuracy和Running time如下表中所示:

Accuracy和Running time这两个性能不太合适综合成单值评价指标。因此,我们可以将Accuracy作为优化指标(Optimizing metic),将Running time作为满意指标(Satisficing metic)。也就是说,给Running time设定一个阈值,在其满足阈值的情况下,选择Accuracy最大的模型。如果设定Running time必须在100ms以内,那么很明显,模型C不满足阈值条件,首先剔除;模型B相比较模型A而言,Accuracy更高,性能更好。
训练、开发、测试集(Train/dev/test distributions)
Train/dev/test sets如何设置对机器学习的模型训练非常重要,合理设置能够大大提高模型训练效率和模型质量。
原则上应该尽量保证dev sets和test sets来源于同一分布且都反映了实际样本的情况。如果dev sets和test sets不来自同一分布,那么我们从dev sets上选择的“最佳”模型往往不能够在test sets上表现得很好。
当样本数量不多(小于一万)的时候,通常将Train/dev/test sets的比例设为60%/20%/20%,在没有dev sets的情况下,Train/test sets的比例设为70%/30%。当样本数量很大(百万级别)的时候,通常将相应的比例设为98%/1%/1%或者99%/1%。
对于dev sets数量的设置,应该遵循的准则是通过dev sets能够检测不同算法或模型的区别,以便选择出更好的模型。
对于test sets数量的设置,应该遵循的准则是通过test sets能够反映出模型在实际中的表现。
实际应用中,可能只有train/dev sets,而没有test sets。这种情况也是允许的,只要算法模型没有对dev sets过拟合。但是,条件允许的话,最好是有test sets,实现无偏估计。
训练、开发、测试集选择设置的一些规则和意见:
- 训练、开发、测试集的设置会对产品带来非常大的影响;
- 在选择开发集和测试集时要使二者来自同一分布,且从所有数据中随机选取;
- 所选择的开发集和测试集中的数据,要与未来想要或者能够得到的数据类似,即模型数据和未来数据要具有相似性;
- 设置的测试集只要足够大,使其能够在过拟合的系统中给出高方差的结果就可以,也许10000左右的数目足够;
- 设置开发集只要足够使其能够检测不同算法、不同模型之间的优劣差异就可以,百万大数据中1%的大小就足够;
改变开发、测试集和评估指标(When to change dev/test sets and metrics)
算法模型的评价标准有时候需要根据实际情况进行动态调整,目的是让算法模型在实际应用中有更好的效果。

概括来说,机器学习可分为两个过程:
- 定义正确的评估指标来更好的给分类器的好坏进行排序;(Define a metric to evaluate classifiers)
- 优化评估指标。(How to do well on this metric)
但是在训练的过程中可能会根据实际情况改变算法模型的评价标准,进行动态调整。
另外一个需要动态改变评价标准的情况是dev/test sets与实际使用的样本分布不一致。比如猫类识别样本图像分辨率差异。

人类表现(Why human-level performance)
机器学习模型的表现通常会跟人类水平表现作比较,如下图所示:
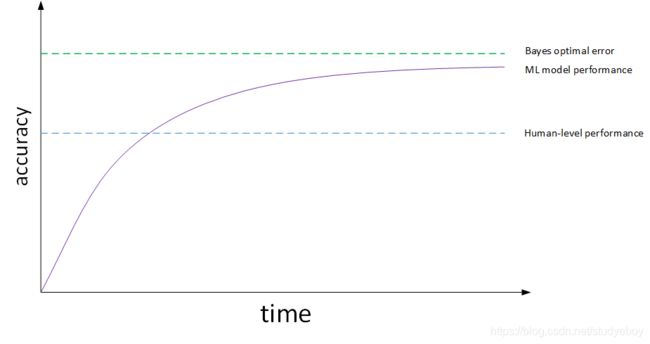
图中,横坐标是训练时间,纵坐标是准确性。机器学习模型经过训练会不断接近human-level performance甚至超过它。但是,超过human-level performance之后,准确性会上升得比较缓慢,最终不断接近理想的最优情况,我们称之为bayes optimal error。理论上任何模型都不能超过它,bayes optimal error代表了最佳表现。
实际上,human-level performance在某些方面有不俗的表现。例如图像识别、语音识别等领域,人类是很擅长的。所以,让机器学习模型性能不断接近human-level performance非常必要也做出很多努力。
可避免偏差(Avoidable bias)
实际应用中,要看human-level error,training error和dev error的相对值。
例如猫类识别的例子中,如果human-level error为1%,training error为8%,dev error为10%。由于training error与human-level error相差7%,dev error与training error只相差2%,所以目标是尽量在训练过程中减小training error,即减小偏差bias。如果图片很模糊,肉眼也看不太清,human-level error提高到7.5%。这时,由于training error与human-level error只相差0.5%,dev error与training error只相差2%,所以目标是尽量在训练过程中减小dev error,即方差variance。这是相对而言的。
对于物体识别这类CV问题,human-level error是很低的,很接近理想情况下的bayes optimal error。因此,上面例子中的1%和7.5%都可以近似看成是两种情况下对应的bayes optimal error。实际应用中,我们一般会用human-level error代表bayes optimal error。
通常,我们把training error与human-level error之间的差值称为bias,也称作avoidable bias;把dev error与training error之间的差值称为variance。根据bias和variance值的相对大小,可以知道算法模型是否发生了欠拟合或者过拟合。
假设针对两个问题分别具有相同的训练误差和交叉验证误差,如下所示:
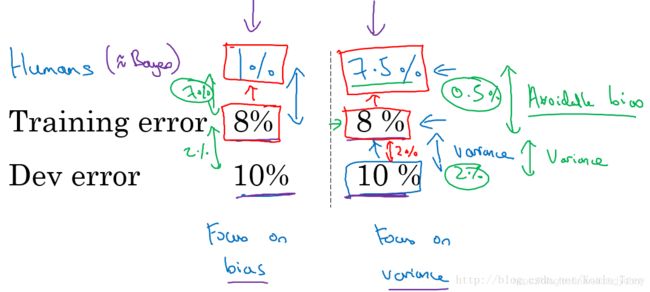
对于左边的问题,人类的误差为1%,对于右边的问题,人类的误差为7.5%。
- 左边的例子:8%与1%差距较大
主要着手减少偏差,即减少训练集误差和人类水平误差之间的差距,来提高模型性能。 - 右边的例子:8%与7.5%接近
主要着手减少方差,即减少开发集误差和测试集误差之间的差距,来提高模型性能
理解人类表现(Understanding human-level performance)
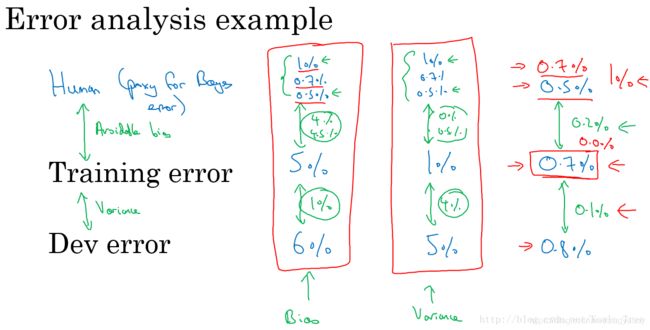
我们说过human-level performance能够代表bayes optimal error。但是,human-level performance如何定义呢?举个医学图像识别的例子,不同人群的error有所不同:
- Typical human : 3% error
- Typical doctor : 1% error
- Experienced doctor : 0.7% error
- Team of experienced doctors : 0.5% error
不同人群他们的错误率不同。一般来说,我们将表现最好的那一组,即Team of experienced doctors作为human-level performance。那么,这个例子中,human-level error就为0.5%。但是实际应用中,不同人可能选择的human-level performance基准是不同的,这会带来一些影响。
假如该模型training error为0.7%,dev error为0.8。如果选择Team of experienced doctors,即human-level error为0.5%,则bias比variance更加突出。如果选择Experienced doctor,即human-level error为0.7%,则variance更加突出。也就是说,选择什么样的human-level error,有时候会影响bias和variance值的相对变化。当然这种情况一般只会在模型表现很好,接近bayes optimal error的时候出现。越接近bayes optimal error,模型越难继续优化,因为这时候的human-level performance可能是比较模糊难以准确定义的。
对人类水平误差有一个大概的估计,可以去估计贝叶斯误差,这样可以更快的做出决定:减少偏差还是减少方差。这个决策技巧通常很有效果,直到系统的性能开始超越人类,那么对贝叶斯误差的估计就不再准确了,再从减少偏差和减少方差方面提升系统性能就会比较困难了。
改善模型的表现(Improving your model performance)
提高机器学习模型性能主要解决两个问题:avoidable bias和variance。training error与human-level error之间的差值反映的是avoidable bias,deverror与training error之间的差值反映的是variance。
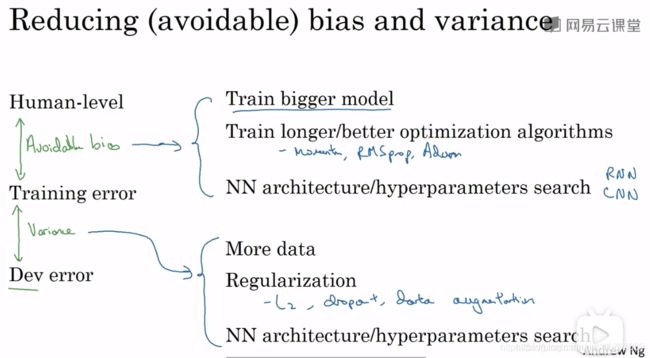
解决avoidable bias常用方法:
- 训练更大的模型
- 训练更长时间、训练更好的优化算法(Momentum、RMSProp、Adam)
- 寻找更好的网络架构(RNN、CNN),寻找更好的超参数
解决variance的常用方法:
- 收集更多的数据
- 正则化(L2、Dropout、数据增强)
- 寻找更好的网络架构(RNN、CNN),寻找更好的超参数
机器学习策略(下)
误差分析(Carrying out error analysis)
对已经建立的机器学习模型进行错误分析(error analysis)十分必要,而且有针对性地、正确地进行error analysis更加重要。
举个例子,猫类识别问题,已经建立的模型的错误率为10%。为了提高正确率,我们发现该模型会将一些狗类图片错误分类成猫。一种常规解决办法是扩大狗类样本,增强模型对够类(负样本)的训练。但是,这一过程可能会花费几个月的时间,耗费这么大的时间成本到底是否值得呢?也就是说扩大狗类样本,重新训练模型,对提高模型准确率到底有多大作用?这时候我们就需要进行error analysis,帮助我们做出判断。
方法很简单,我们可以从分类错误的样本中统计出狗类的样本数量。根据狗类样本所占的比重,判断这一问题的重要性。假如狗类样本所占比重仅为5%,即时我们花费几个月的时间扩大狗类样本,提升模型对其识别率,改进后的模型错误率最多只会降低到9.5%。相比之前的10%,并没有显著改善。我们把这种性能限制称为ceiling on performance。相反,假如错误样本中狗类所占比重为50%,那么改进后的模型错误率有望降低到5%,性能改善很大。因此,值得去花费更多的时间扩大狗类样本。
这种error analysis虽然简单,但是能够避免花费大量的时间精力去做一些对提高模型性能收效甚微的工作,让我们专注解决影响模型正确率的主要问题,十分必要。
这种error analysis可以同时评估多个影响模型性能的因素,通过各自在错误样本中所占的比例来判断其重要性。
通常来说,比例越大,影响越大,越应该花费时间和精力着重解决这一问题。这种error analysis让我们改进模型更加有针对性,从而提高效率。
清除错误标记的样本(Cleaning up incorrectly labeled data)
监督式学习中,训练样本有时候会出现输出y标注错误的情况,即incorrectly labeled examples。
- 如果训练样本中出现incorrectly labeled data
如果这些label标错的情况是随机性的(random errors),DL算法对其包容性是比较强的,即健壮性好,一般可以直接忽略,无需修复。然而,如果是系统错误(systematic errors),这将对DL算法造成影响,降低模型性能。例如:做标记的人一直把例子中白色的狗标记成猫,那么最终导致分类器出现错误。 - 如果dev/test sets中出现incorrectly labeled data
利用error analysis,统计dev sets中所有分类错误的样本中incorrectly labeled data所占的比例。根据该比例的大小,决定是否需要修正所有incorrectly labeled data,还是可以忽略。
例如dev/test sets中出现incorrectly labeled data。

dev set的主要作用是在不同的算法之间进行比较,选择错误率最小的算法模型。但是如果有incorrectly labeled data的存在,当不同算法错误率比较接近的时候,无法仅仅根据Overall dev set error准确指出哪个算法模型更好,必须修正incorrectly labeled data。
关于修正开发、测试集上错误样例(incorrectly dev/test set data)的建议:
- 对开发集和测试集上的数据进行检查,确保他们来自于相同的分布。使得我们以开发集为目标方向,更正确地将算法应用到测试集上。(Apply same process to your dev and test sets to make sure they continue to come from the same distribution)
- 考虑算法分类错误的样本的同时也去考虑算法分类正确的样本。(通常难度比较大,很少这么做)(Consider examining examples your algorithm got right as well as ones it got wrong)
- 训练集和开发/测试集来自不同的分布。(Train and dev/test data may now come from slightly different distributions)
搭建系统(Build your first system quickly then iterate)
如果我们想建立自己的深度学习系统,我们就需要做到:快速的建立自己的基本系统,并进行迭代。而不是想的太多,在一开始就建立一个非常复杂,难以入手的系统。
- 设置开发、测试集和优化指标(确定方向);(Set up dev/test set and metric)
- 快速地建立基本的系统;(Build initial system quickly)
- 使用偏差方差分析、误差分析去确定后面步骤的优先步骤。(Use Bias/Variance analysis & Error analysis to prioritize next steps)
不同分布上的训练和测试(Training and testing on different distribution)
当train set与dev/test set不来自同一个分布的时候,我们应该如何解决这一问题,构建准确的机器学习模型呢?
以猫类识别为例,train set来自于网络下载(webpages),图片比较清晰;dev/test set来自用户手机拍摄(mobile app),图片比较模糊。假如train set的大小为200000,而dev/test set的大小为10000,显然train set要远远大于dev/test set。

虽然dev/test set质量不高,但是模型最终主要应用在对这些模糊的照片的处理上。面对train set与dev/test set分布不同的情况,有两种解决方法。
第一种方法是将train set和dev/test set完全混合,然后在随机选择一部分作为train set,另一部分作为dev/test set。例如,混合210000例样本,然后随机选择205000例样本作为train set,2500例作为dev set,2500例作为test set。这种做法的优点是实现train set和dev/test set分布一致,缺点是dev/test set中webpages图片所占的比重比mobile app图片大得多。例如dev set包含2500例样本,大约有2381例来自webpages,只有119例来自mobile app。这样,dev set的算法模型对比验证,仍然主要由webpages决定,实际应用的mobile app图片所占比重很小,达不到验证效果。因此,这种方法并不是很好。
第二种方法是将原来的train set和一部分dev/test set组合当成train set,剩下的dev/test set分别作为dev set和test set。例如,200000例webpages图片和5000例mobile app图片组合成train set,剩下的2500例mobile app图片作为dev set,2500例mobile app图片作为test set。其关键在于dev/test set全部来自于mobile app。这样保证了验证集最接近实际应用场合。这种方法较为常用,而且性能表现比较好。
不同分布上的偏差和方差(Bias and Variance with mismatched data distributions)
根据human-level error、training error和dev error的相对值可以判定是否出现了bias或者variance。但是,如果train set和dev/test set来源于不同分布,则无法直接根据相对值大小来判断。例如某个模型human-level error为0%,training error为1%,dev error为10%。显然该模型出现了variance。但是,training error与dev error之间的差值9%可能来自算法本身(variance),也可能来自于样本分布不同。比如dev set都是很模糊的图片样本,本身就难以识别,跟算法模型关系不大。因此不能简单认为出现了variance。
在可能存在train set与dev/test set分布不一致的情况下,定位是否出现variance的方法是设置train-dev set。从原来的train set中分割出一部分作为train-dev set,train-dev set不作为训练模型使用,而是与dev set一样用于验证。
这样,我们就有training error、training-dev error和dev error三种error。其中,training error与training-dev error的差值反映了variance;training-dev error与dev error的差值反映了data mismatch problem,即样本分布不一致。如果training error为1%,training-dev error为9%,dev error为10%,则variance问题比较突出。如果training error为1%,training-dev error为1.5%,dev error为10%,则data mismatch problem比较突出。通过引入train-dev set,能够比较准确地定位出现了variance还是data mismatch。
human-level error、training error、training-dev error、dev error以及test error之间的差值关系和反映的问题:

一般情况下,human-level error、training error、training-dev error、dev error以及test error的数值是递增的,但是也会出现dev error和test error下降的情况。这主要可能是因为训练样本比验证/测试样本更加复杂,难以训练。
解决数据分布不匹配问题(Addressing data mismatch)
解决train set与dev/test set样本分布不一致的问题:
- 进行人工误差分析,尝试去了解训练集和开发测试集的具体差异在哪里。如:噪音等;
- 尝试把训练数据变得更像开发集,或者收集更多的类似开发集和测试集的数据,如增加噪音;
为了让train set与dev/test set类似,我们可以使用人工数据合成的方法(artificial data synthesis)。
迁移学习(Transfer learning)
深度学习非常强大的一个功能之一就是有时候你可以将已经训练好的模型的一部分知识(网络结构)直接应用到另一个类似模型中去。这种学习方法被称为迁移学习(Transfer Learning)。
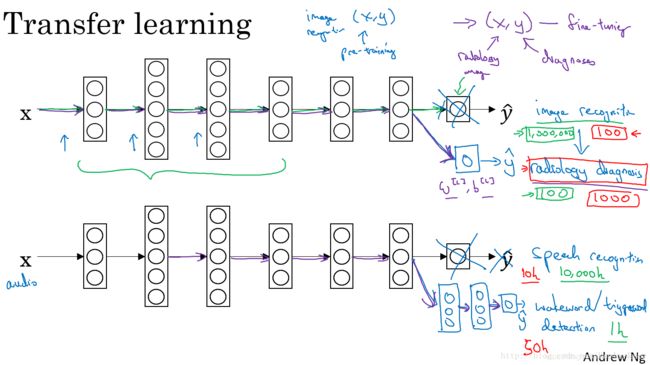
迁移学习,重新训练权重系数,如果需要构建新模型的样本数量较少,那么可以像刚才所说的,只训练输出层的权重系数 W [ L ] W^{[L]} W[L], b [ L ] b^{[L]} b[L],保持其它层所有的权重系数 W [ L ] W^{[L]} W[L], b [ L ] b^{[L]} b[L]不变。这种做法相对来说比较简单。如果样本数量足够多,那么也可以只保留网络结构,重新训练所有层的权重系数。这种做法使得模型更加精确,因为毕竟样本对模型的影响最大。选择哪种方法通常由数据量决定。
迁移学习之所以能这么做的原因是,神经网络浅层部分能够检测出许多图片固有特征,例如图像边缘、曲线等。使用之前训练好的神经网络部分结果有助于我们更快更准确地提取特征。二者处理的都是图片,而图片处理是有相同的地方,第一个训练好的神经网络已经帮我们实现如何提取图片有用特征了。 因此,即便是即将训练的第二个神经网络样本数目少,仍然可以根据第一个神经网络结构和权重系数得到健壮性好的模型。
迁移学习可以保留原神经网络的一部分,再添加新的网络层。具体问题,具体分析,可以去掉输出层后再增加额外一些神经层。
迁移学习有意义的情况:
- 任务A和任务B有着相同的输入;
- 任务A所拥有的数据要远远大于任务B(对于更有价值的任务B,任务A所拥有的数据要比B大很多);
- 任务A的低层特征学习对任务B有一定的帮助;
多任务学习(Multi-task learning)


多任务学习是使用单个神经网络模型来实现多个任务。实际上,也可以分别构建多个神经网络来实现。但是,如果各个任务之间是相似问题(例如都是图片类别检测),则可以使用多任务学习模型。另外,多任务学习中,可能存在训练样本Y某些label空白的情况,这并不影响多任务模型的训练。
多任务学习的应用场合:
- 如果训练的一组任务可以共用低层特征;
- 通常,对于每个任务大量的数据具有很大的相似性;(如,在迁移学习中由任务A“100万数据”迁移到任务B“1000数据”;多任务学习中,任务 A 1 , . . . , A n A_{1},...,A_{n} A1,...,An,每个任务均有1000个数据,合起来就有1000n个数据,共同帮助任务的训练)
- 可以训练一个足够大的神经网络并同时做好所有的任务。
迁移学习和多任务学习在实际应用中,迁移学习使用得更多一些。
端到端深度学习(What is end-to-end deep learning)
端到端(end-to-end)深度学习就是将所有不同阶段的数据处理系统或学习系统模块组合在一起,用一个单一的神经网络模型来实现所有的功能。它将所有模块混合在一起,只关心输入和输出。
以语音识别为例,传统的算法流程和end-to-end模型的区别如下:

如果训练样本足够大,神经网络模型足够复杂,那么end-to-end模型性能比传统机器学习分块模型更好。实际上,end-to-end让神经网络模型内部去自我训练模型特征,自我调节,增加了模型整体契合度。
end-to-end深度学习有优点也有缺点。
- 优点:
- 端到端学习可以直接让数据“说话”;
- 所需手工设计的组件更少。
- 缺点:
- 需要大量的数据;
- 排除了可能有用的手工设计组件。
卷积神经网络
卷积神经网络基础
计算机视觉(Computer Vision)
计算机视觉(Computer Vision)包含很多不同类别的问题,如图片分类、目标检测、图片风格迁移等等。
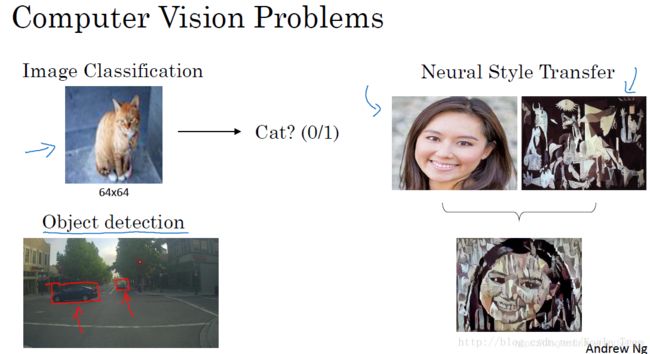
对于小尺寸的图片问题,也许我们用深度神经网络的结构可以较为简单的解决一定的问题。但是当应用在大尺寸的图片上,输入规模将变得十分庞大,使用神经网络将会有非常多的参数需要去学习,这个时候神经网络就不再适用。
卷积神经网络在计算机视觉问题上是一个非常好的网络结构。
边缘检测示例(Edge Detection Example)
图片的边缘检测可以通过与相应滤波器进行卷积来实现。
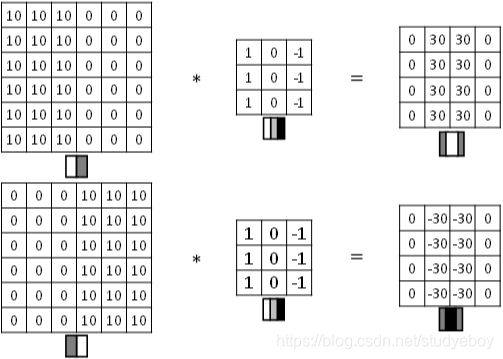
图片边缘有两种渐变方式,一种是由明变暗,另一种是由暗变明。以垂直边缘检测为例,下图展示了两种方式的区别。实际应用中,这两种渐变方式并不影响边缘检测结果,可以对输出图片取绝对值操作,得到同样的结果。
垂直边缘检测和水平边缘检测的滤波器算子如下所示:
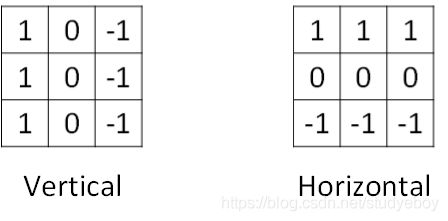
除了简单的Vertical、Horizontal滤波器之外,还有其它常用的filters,例如Sobel filter和Scharr filter。这两种滤波器的特点是增加图片中心区域的权重。
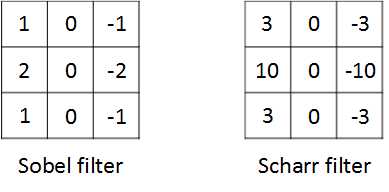
在深度学习中,如果我们想检测图片的各种边缘特征,而不仅限于垂直边缘和水平边缘,那么filter的数值一般需要通过模型训练得到,类似于标准神经网络中的权重W一样由梯度下降算法反复迭代求得。CNN的主要目的就是计算出这些filter的数值。确定得到了这些filter后,CNN浅层网络也就实现了对图片所有边缘特征的检测。
在数学定义上,矩阵的卷积(convolution)操作为首先将卷积核同时在水平和垂直方向上进行翻转,构成一个卷积核的镜像,然后使用该镜像再和前面的矩阵进行移动相乘求和操作。如下面例子所示:
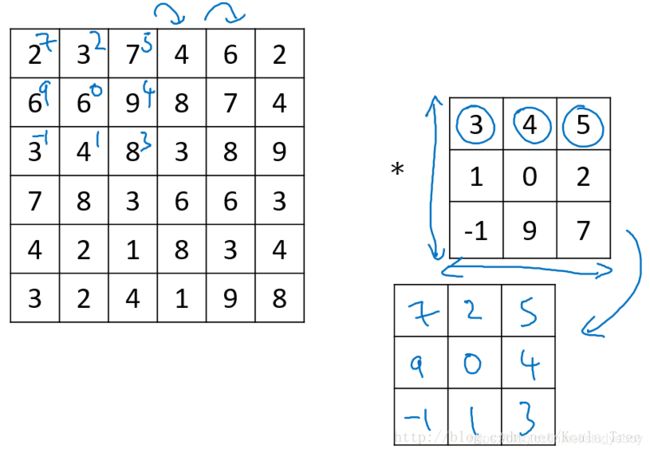
在深度学习中,我们称为的卷积运算实则没有卷积核变换为镜像的这一步操作,因为在权重学习的角度,变换是没有必要的。深度学习的卷积操作在数学上准确度来说称为互相关(cross-correlation)。
但是,为了简化计算,我们一般把CNN中的这种“相关系数”就称作卷积运算。之所以可以这么等效,是因为滤波器算子一般是水平或垂直对称的,180度旋转影响不大;而且最终滤波器算子需要通过CNN网络梯度下降算法计算得到,旋转部分可以看作是包含在CNN模型算法中。总的来说,忽略旋转运算可以大大提高CNN网络运算速度,而且不影响模型性能。
padding
按照我们上面讲的图片卷积,如果原始图片尺寸为n x n,filter尺寸为f x f,则卷积后的图片尺寸为(n-f+1) x (n-f+1),注意f一般为奇数。这样会带来两个问题:
- 卷积运算后,输出图片尺寸缩小
- 原始图片边缘信息对输出贡献得少,输出图片丢失边缘信息
为了解决图片缩小的问题,可以使用padding方法,即把原始图片尺寸进行扩展,扩展区域补零,用p来表示每个方向扩展的宽度。
经过padding之后,原始图片尺寸为(n+2p) x (n+2p),filter尺寸为f x f,则卷积后的图片尺寸为(n+2p-f+1) x (n+2p-f+1)。若要保证卷积前后图片尺寸不变,则p应满足:
p = f − 1 2 p=\frac{f-1}{2} p=2f−1
没有padding操作,p=0,我们称之为“Valid convolutions”;有padding操作, p = f − 1 2 p=\frac{f-1}{2} p=2f−1,我们称之为“Same convolutions”。
卷积步长(Strided Convolutions)
Stride表示filter在原图片中水平方向和垂直方向每次的步进长度。之前我们默认stride=1。若stride=2,则表示filter每次步进长度为2,即隔一点移动一次。
![]()
我们用s表示stride长度,p表示padding长度,如果原始图片尺寸为n x n,filter尺寸为f x f,则卷积后的图片尺寸为:
⌊ n + 2 p − f s + 1 ⌋ × ⌊ n + 2 p − f s + 1 ⌋ \lfloor\frac{n+2p-f}{s}+1\rfloor\ \times \ \lfloor\frac{n+2p-f}{s}+1\rfloor ⌊sn+2p−f+1⌋ × ⌊sn+2p−f+1⌋
上式中, ⌊ ⋯ ⌋ \lfloor\cdots\rfloor ⌊⋯⌋表示向下取整。
立体卷积(Convolutions Over Volume)
对于3通道的RGB图片,其对应的滤波器算子同样也是3通道的。例如一个图片是6 x 6 x 3,分别表示图片的高度(height)、宽度(weight)和通道(#channel)。
3通道图片的卷积运算与单通道图片的卷积运算基本一致。过程是将每个单通道(R,G,B)与对应的filter进行卷积运算求和,然后再将3通道的和相加,得到输出图片的一个像素值。
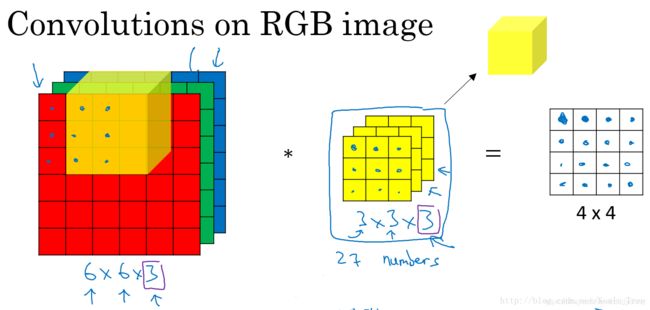
不同通道的滤波算子可以不相同。例如R通道filter实现垂直边缘检测,G和B通道不进行边缘检测,全部置零,或者将R,G,B三通道filter全部设置为水平边缘检测。
为了进行多个卷积运算,实现更多边缘检测,可以增加更多的滤波器组。例如设置第一个滤波器组实现垂直边缘检测,第二个滤波器组实现水平边缘检测。这样,不同滤波器组卷积得到不同的输出,个数由滤波器组决定。
![]()

卷积神经网络的单层结构(One Layer of a Convolutional Network)
和普通的神经网络单层前向传播的过程类似,卷积神经网络也是一个先由输入和权重及偏置做线性运算,然后得到的结果输入一个激活函数中,得到最终的输出:
z [ 1 ] = w [ 1 ] a [ 0 ] + b [ 1 ] a [ 1 ] = g ( z [ 1 ] ) z^{[1]}=w^{[1]}a^{[0]}+b^{[1]}\\a^{[1]}=g(z^{[1]}) z[1]=w[1]a[0]+b[1]a[1]=g(z[1])
不同点是在卷积神经网络中,权重和输入进行的是卷积运算。
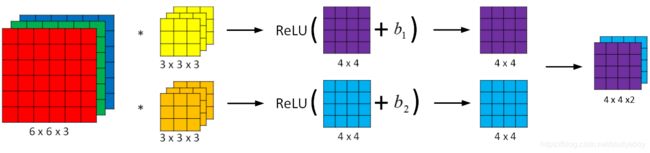
相比之前的卷积过程,CNN的单层结构多了激活函数ReLU和偏移量b。整个过程与标准的神经网络单层结构非常类似:
Z [ l ] = W [ l ] A [ l − 1 ] + b A [ l ] = g [ l ] ( Z [ l ] ) Z^{[l]}=W^{[l]}A^{[l-1]}+b \\ A^{[l]}=g^{[l]}(Z^{[l]}) Z[l]=W[l]A[l−1]+bA[l]=g[l](Z[l])
卷积运算对应着上式中的乘积运算,滤波器组数值对应着权重 W [ l ] W^{[l]} W[l],所选的激活函数为ReLU。
计算上图中参数的数目:每个滤波器组有3x3x3=27个参数,还有1个偏移量b,则每个滤波器组有27+1=28个参数,两个滤波器组总共包含28x2=56个参数。我们发现,选定滤波器组后,参数数目与输入图片尺寸无关。所以,就不存在由于图片尺寸过大,造成参数过多的情况。例如一张1000x1000x3的图片,标准神经网络输入层的维度将达到3百万,而在CNN中,参数数目只由滤波器组决定,数目相对来说要少得多,这是CNN的优势之一。
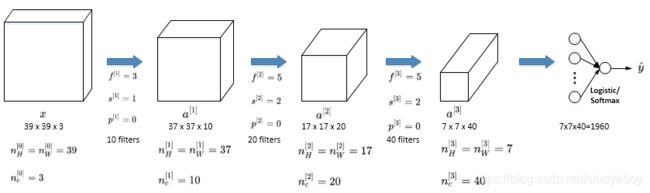
简单卷积网络示例(Simple Convolutional Network Example)
池化层(Pooling Layers)
Pooling layers是CNN中用来减小尺寸,提高运算速度的,同样能减小noise影响,让各特征更具有健壮性。
Pooling layers的做法比convolution layers简单许多,没有卷积运算,仅仅是在滤波器算子滑动区域内取最大值,即max pooling,这是最常用的做法。注意,超参数p很少在pooling layers中使用。
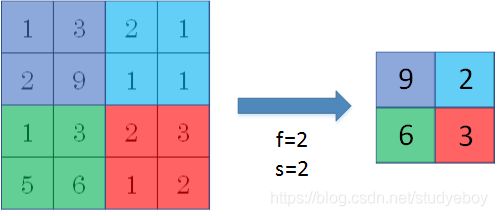
Max pooling的好处是只保留区域内的最大值(特征),忽略其它值,降低noise影响,提高模型健壮性。而且,max pooling需要的超参数仅为滤波器尺寸f和滤波器步进长度s,没有其他参数需要模型训练得到,计算量很小。

如果是多个通道,那么就每个通道单独进行max pooling操作。
除了max pooling之外,还有一种做法:average pooling。顾名思义,average pooling就是在滤波器算子滑动区域计算平均值。
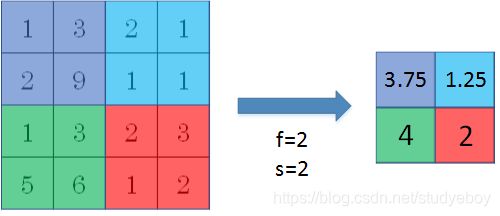
卷积神经网络示例(CNN Example)
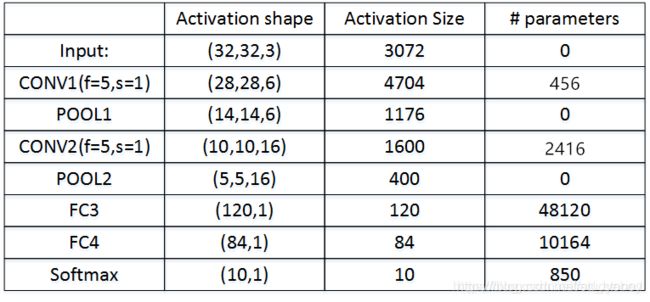
下面介绍一个简单的数字识别的CNN例子:

图中,CON层后面紧接一个POOL层,CONV1和POOL1构成第一层,CONV2和POOL2构成第二层。特别注意的是FC3和FC4为全连接层FC,它跟标准的神经网络结构一致。最后的输出层(softmax)由10个神经元构成。
使用卷积神经网络(Why Convolutions)
相比标准神经网络,CNN的优势之一就是参数数目要少得多。参数数目少的原因有两个:
- 参数共享:一个特征检测器(例如垂直边缘检测)对图片某块区域有用,同时也可能作用在图片其它区域。
- 连接的稀疏性:因为滤波器算子尺寸限制,每一层的每个输出只与输入部分区域内有关。
除此之外,由于CNN参数数目较小,所需的训练样本就相对较少,从而一定程度上不容易发生过拟合现象。而且,CNN比较擅长捕捉区域位置偏移。也就是说CNN进行物体检测时,不太受物体所处图片位置的影响,增加检测的准确性和系统的健壮性。
卷积神经网络实例模型
经典的卷积网络(Classic Networks)
LeNet-5(1998)
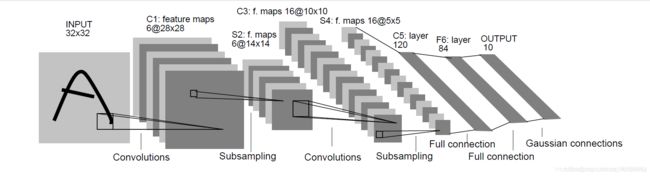
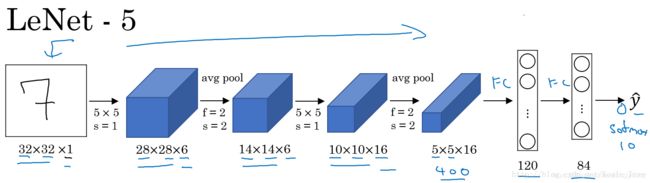
LeNet-5模型是Yann LeCun教授于1998年提出来的,它是第一个成功应用于数字识别问题的卷积神经网络。在MNIST数据中,它的准确率达到大约99.2%。典型的LeNet-5结构包含CONV layer,POOL layer和FC layer,顺序一般是CONV layer->POOL layer->CONV layer->POOL layer->FC layer->FC layer->OUTPUT layer,即 y ^ \hat y y^。该LeNet模型总共包含了大约6万个参数。值得一提的是,当时Yann LeCun提出的LeNet-5模型池化层使用的是average pool,而且各层激活函数一般是Sigmoid和tanh。现在,我们可以根据需要,做出改进,使用max pool和激活函数ReLU。下图所示的是一个数字识别的LeNet-5的模型结构:

- conv1 16个过滤器,过滤器尺寸为5,步长为1,填充为0
- pool1过滤器尺寸为2,步长为2
- conv2 16个过滤器,过滤器尺寸为5,步长为1,填充为0
- pool2 过滤器尺寸为2,步长为2
- fc3 全连接层120个神经元
- fc4 全连接层84个神经元
- output输出层10个神经元 softmax回归
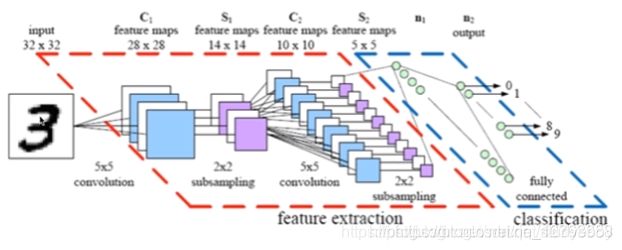
注意:
- 在LeNet-5中,池化后会加入非线性函数sigmoid
- 在当时LeNet-5用的是平均池化,现在通常使用最大池化
- 在当时LeNet-5用的不是Softmax回归进行分类,而是用的另一种小众的方法。
AlexNet(2012)
AlexNet模型是由Alex Krizhevsky、Ilya Sutskever和Geoffrey Hinton共同提出的,AlexNet模型与LeNet-5模型类似,只是要复杂一些,总共包含了大约6千万个参数。同样可以根据实际情况使用激活函数ReLU。原作者还提到了一种优化技巧,叫做Local Response Normalization(LRN)。 而在实际应用中,LRN的效果并不突出。其结构如下所示:
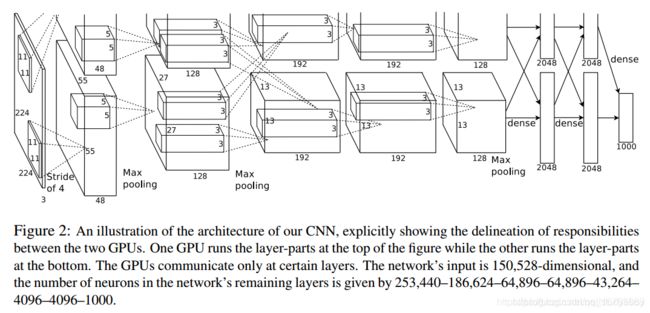
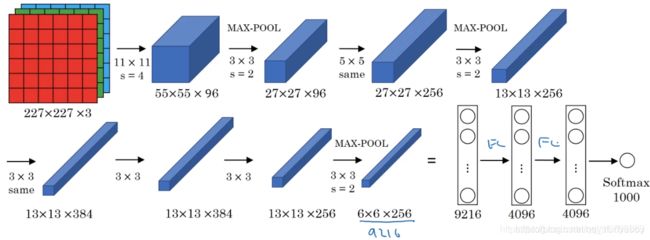
- conv1 96个过滤器,过滤器尺寸为11,步长为4,填充为0
- pool1 过滤器尺寸为3,步长为2
- conv2 256个过滤器,过滤器尺寸为5,有填充保证卷积后尺寸不变
- pool2 过滤器尺寸为3,步长为2
- conv3 384个过滤器,过滤器尺寸为3,有填充保证卷积后尺寸不变
- conv4 384个过滤器,过滤器尺寸为3,有填充保证卷积后尺寸不变
- conv5 256个过滤器,过滤器尺寸为3,有填充保证卷积后尺寸不变
- pool5 过滤器尺寸为3,步长为2
- fc6 全连接4096个神经元
- fc7 全连接4096个神经元
- output 输出1000个神经元 softmax回归
- 虽然AlexNet和LeNet-5相似,但是AlexNet比LeNet-5大得多
- AlexNet可以处理相似的基本构造模块,这些模块往往包含大量隐藏单元和数据。
- AlexNet使用了ReLU激活函数
- 在当时GPU处理速度还很慢,采用的是在两个GPU上训练,将每一层拆到两个GPU上工作。
- AlexNet论文中提到的LRN(局部响应归一化层),现在发现这样做并没有多好,所以现在并不用LRN层训练网络。
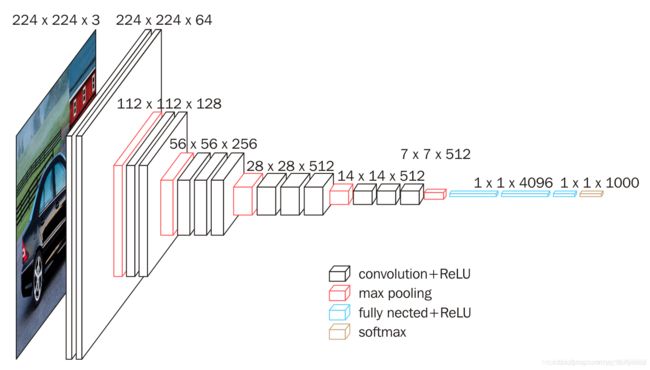
VGG-16(2015)
- VGG-16一共是16层卷积层加全连接层
- 这种网络结构非常工整,卷积层专注于尺寸为3的过滤器,步长为1,padding类型为same;池化层专注于尺寸为2的过滤器,步长为2.
- 在多个卷积层后跟一共压缩尺寸的池化层。
- 每一层的通道数和图像高宽都呈现明显的2倍规律
- 缺点是训练的特征数量非常大
ResNet
如果神经网络层数越多,网络越深,源于梯度消失和梯度爆炸的影响,整个模型难以训练成功。解决的方法之一是人为地让神经网络某些层跳过下一层神经元的连接,隔层相连,弱化每层之间的强联系。这种神经网络被称为Residual Networks(ResNets)。
Residual Networks由许多隔层相连的神经元子模块组成,我们称之为Residual block。单个Residual block的结构如下图所示:
![]()

该模型由Kaiming He, Xiangyu Zhang, Shaoqing Ren和Jian Sun共同提出。由多个Residual block组成的神经网络就是Residual Network。实验表明,这种模型结构对于训练非常深的神经网络,效果很好。另外,为了便于区分,我们把非Residual Networks称为Plain Network。
与Plain Network相比,Residual Network能够训练更深层的神经网络,有效避免发生发生梯度消失和梯度爆炸。从下面两张图的对比中可以看出,随着神经网络层数增加,Plain Network实际性能会变差,training error甚至会变大。然而,Residual Network的训练效果却很好,training error一直呈下降趋势。
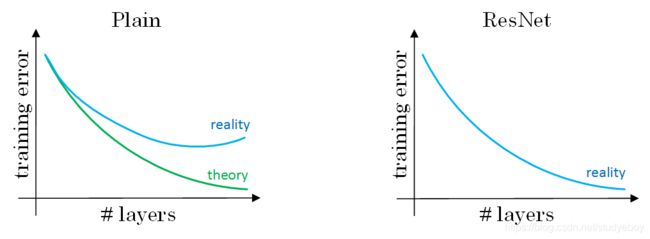
- 在没有残差的普通神经网络中,训练的误差实际上是随着网络层数的加深,先减小再增加;
- 在有残差的ResNet中,即使网络再深,训练误差都会随着网络层数的加深逐渐减小。
ResNet对于中间的激活函数来说,有助于能够达到更深的网络,解决梯度消失和梯度爆炸的问题。
ResNet表现好的原因(Why ResNets Work)
下面用个例子来解释为什么ResNets能够训练更深层的神经网络。
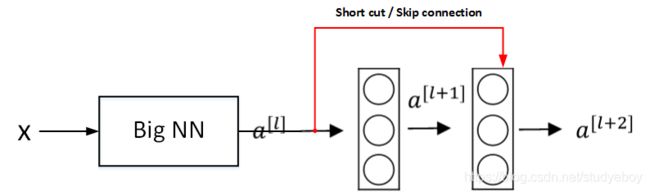

将普通深度神经网络变为ResNet:

ResNets同类型层之间,例如CONV layers,大多使用same类型,保持维度相同。如果是不同类型层之间的连接,例如CONV layer与POOL layer之间,如果维度不同,则引入矩阵Ws。
1x1卷积(Networks in Networks and 1x1 Convolutions)
Min Lin, Qiang Chen等人提出了一种新的CNN结构,即1x1 Convolutions,也称Networks in Networks。这种结构的特点是滤波器算子filter的维度为1x1。对于单个filter,1x1的维度,意味着卷积操作等同于乘积操作。
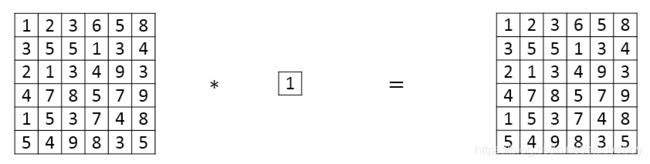

那么,对于多个filters,1x1 Convolutions的作用实际上类似全连接层的神经网络结构。效果等同于Plain Network中 a [ l ] a^{[l]} a[l]到 a [ l + 1 ] a^{[l+1]} a[l+1]的过程。
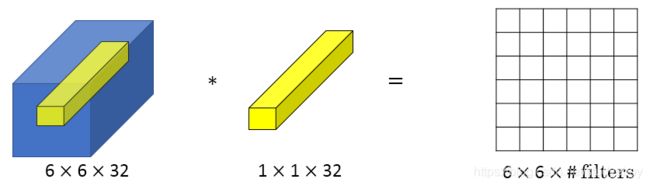
1x1 Convolutions可以用来缩减输入图片的通道数目。方法如下图所示:

在上图中,将192个通道压缩到32个,那么过滤器1x1x192,用了32个过滤器。与之形成对对的是池化层,池化层将宽和高压缩的更小,而通道数不改变。如果用的是192个过滤器,那么卷积后结果仍然是28x28
x192,但是也发生了改变,加入了一次ReLU激活函数,可以学习更复杂的函数。
1x1卷积应用:
- 维度压缩:使用目标维度的 1 × 1 1\times1 1×1的卷积核个数。
- 增加非线性:保持与原维度相同的 1 × 1 1\times1 1×1的卷积核个数。
Inception Network Motivation
CNN单层的滤波算子filter尺寸是固定的,1x1或者3x3等。而Inception Network在单层网络上可以使用多个不同尺寸的filters,进行same convolutions,把各filter下得到的输出拼接起来。除此之外,还可以将CONV layer与POOL layer混合,同时实现各种效果。但是要注意使用same pool。

Inception Network由Christian Szegedy, Wei Liu等人提出。与其它只选择单一尺寸和功能的filter不同,Inception Network使用不同尺寸的filters并将CONV和POOL混合起来,将所有功能输出组合拼接,再由神经网络本身去学习参数并选择最好的模块。
Inception Network在提升性能的同时,会带来计算量大的问题。例如下面这个例子:

- filters: 5 × 5 × 192 5\times5\times192 5×5×192;
- 32 个 filters;
- 总的计算成本: 28 × 28 × 32 × 5 × 5 × 192 = 120 M 28\times28\times32\times5\times5\times192=120M 28×28×32×5×5×192=120M
引入1x1 Convolutions来减少其计算量,结构如下图所示:

- 1×1卷积层计算成本: 28 × 28 × 16 × 1 × 1 × 192 = 2.4 M 28\times28\times16\times1\times1\times192=2.4M 28×28×16×1×1×192=2.4M
- 5 × 5 5\times5 5×5卷积层计算成本: 28 × 28 × 32 × 5 × 5 × 16 = 10.0 M 28\times28\times32\times5\times5\times16=10.0M 28×28×32×5×5×16=10.0M
- 总的计算成本:2.4 M + 10.0 M = 12.4 M
虽然多引入了1x1 Convolution层,但是总共的计算量减少了近90%,效果还是非常明显的。由此可见,1x1 Convolutions还可以有效减少CONV layer的计算量。
所以 1 × 1 1\times1 1×1卷积核作为bottleneck layer”的过渡层能够有效减小卷积神经网的计算成本。事实证明,只要合理地设置“bottleneck layer”,既可以显著减小上层的规模,同时又能降低计算成本,从而不会影响网络的性能。
Inception Network
使用1x1 Convolution来减少Inception Network计算量大的问题。引入1x1 Convolution后的Inception module如下图所示:

多个Inception modules组成Inception Network,效果如下图所示:
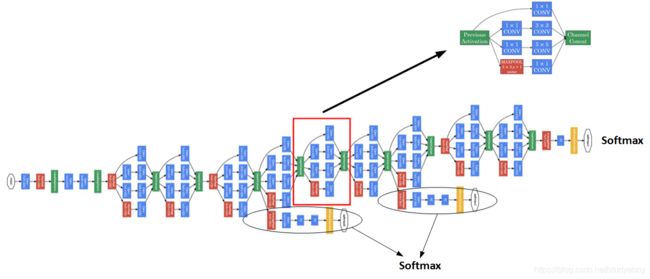
上述Inception Network除了由许多Inception modules组成之外,值得一提的是网络中间隐藏层也可以作为输出层Softmax,有利于防止发生过拟合。
数据扩充(Data Augmentation)
常用的Data Augmentation方法是对已有的样本集进行Mirroring和Random Cropping。
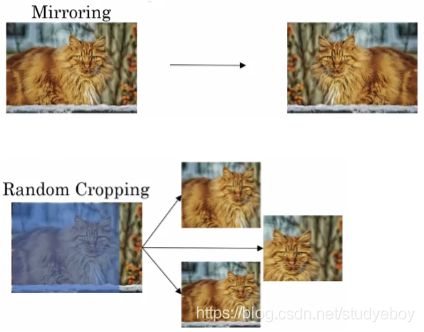
另一种Data Augmentation的方法是color shifting。color shifting就是对图片的RGB通道数值进行随意增加或者减少,改变图片色调。
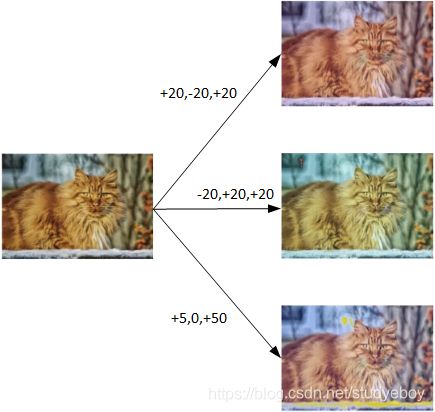
除了随意改变RGB通道数值外,还可以更有针对性地对图片的RGB通道进行PCA color augmentation,也就是对图片颜色进行主成分分析,对主要的通道颜色进行增加或减少,可以采用高斯扰动做法。这样也能增加有效的样本数量。
计算机视觉现状(State of Computer Vision)
神经网络需要数据,不同的网络模型所需的数据量是不同的。Object detection、Image recognition、Speech recognition所需的数据量依次增加。一般来说,如果data较少,那么就需要更多的hand-engineering,对已有data进行处理,例如data augmentation。模型算法也会相对要复杂一些。如果data很多,可以构建深层神经网络,不需要太多的hand-engineering,模型算法也就相对简单一些。

在模型研究或者竞赛方面,有一些方法能够有助于提升神经网络模型的性能:
- Ensembling:Train several Networks independently and average their outputs。
- Multi-crop at test time:Run classifier on multiple versions of test images and average results。
但是由于这两种方法计算成本较大,一般不适用于实际项目开发。
还需要灵活使用开源代码:
- Use architectures of networks published in the literature
- Use open source implementations if possible
- Use pretrained models and fine-tune on your dataset
目标检测
目标定位(Object Localization)
除了利用CNN模型进行图像分类,还可以进行目标定位和目标检测(包括多目标检测)。
- 分类问题:判断图中是否为汽车;
- 目标定位:判断是否为汽车,并确定具体位置;
- 目标检测:检测不同物体并定位。
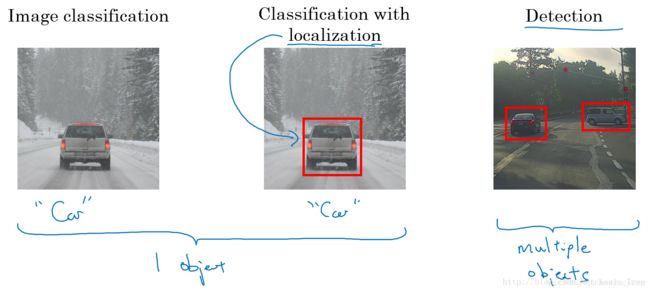
标准的CNN分类模型如下所示,原始图片经过conv卷积之后,softmax层输出4x1向量,分别对应pedestrian、car、motorcycle和background四类。
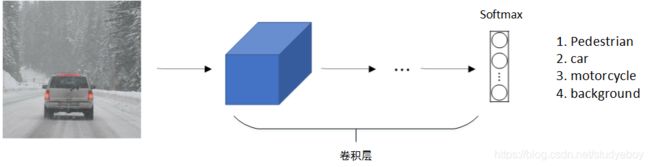
对于目标定位和目标检测问题,其模型如下所示,原始图像经过conv卷积之后,softmax层输出8x1向量,除了包含CNN分类3x1向量(class label)之外,还包括(bx,by)表示目标中心位置坐标,(bh,bw)表示目标所在矩形区域的高和宽,Pc表示矩形区域是目标的概率,数值在0-1之间,且越大概率越大。一般设定图像左上角为原点(0,0),右下角为(1,1)。这些数字均为位置或长度所在图像的比例大小。在模型训练时,bx,by,bh,bw都由人为确定其数值。例如bx=0.5,by=0.7,bh=0.3, bw=0.4。

对于损失函数,在实际应用中:
- 对 c 1 、 c 2 、 c 3 c_{1}、c_{2}、c_{3} c1、c2、c3 和softmax使用对数似然损失函数;
- 对边界框的四个值应用平方误差或者类似的方法;
- P c P_c Pc 应用logistic regression损失函数,或者平方预测误差。
特征点检测(Landmark Detection)
除了使用矩形区域检测目标类别和位置外,我们还可以仅对目标的关键特征点坐标进行定位,这些关键点被称为landmarks。
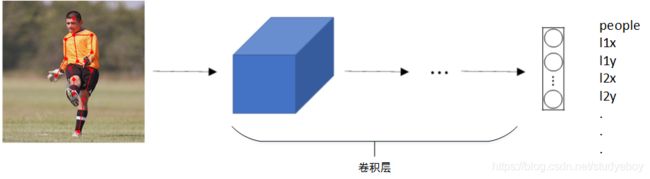
例如人脸识别,可以对人脸部分特征点坐标进行定位检测,并标记出来,如下图所示,该网络模型共检测人脸上64个特征点,加上是否为face的标志位,输出label共64x2+1=129个值。通过人脸特征点检测可以进行情绪分类与判断,或者应用于AR领域等等。

除了人脸特征点检测之外,还可以检测人体姿势动作,如下图所示。
目标检测(Object Detection)
目标检测的一种简单方法是滑动窗算法。这种算法首先在训练样本集上搜集相应的各种目标图片和非目标图片。注意训练集图片尺寸较小,尽量仅包含相应目标,对训练集中的图片进行标注,有目标物体的标注1,没有目标物体的标准0。然后,使用这些训练集构建CNN模型,使得模型有较高的识别率。如下图所示:

最后,在测试图片上,选择大小适宜的窗口、合适的步进长度,进行从左到右、从上到下的滑动。每个窗口区域都送入之前构建好的CNN模型进行识别判断。若判断有目标,则此窗口即为目标区域;若判断没有目标,则此窗口为非目标区域。遍历整个图像,可以保证在每个位置都能检测到是否有目标物体。

滑动窗口算法优点是原理简单,且不需要认为选定目标区域(检测出目标的滑动窗口即为目标区域)。但是缺点也很明显,首先滑动窗口的大小和步进长度都需要人为直观设定。滑动窗过小或过大,步进长度过大均会降低目标检测正确率。而且,每次滑动窗口区域都要进行一次CNN网络计算,如果滑动窗和步进长度较小,整个目标检测的算法运行时间会很长。所以,滑动窗口算法虽然简单,但是性能不佳,计算成本大,不够灵活。
卷积代替滑窗(Convolutional Implementation of Sliding Windows)
滑动窗口算法可以使用卷积方式实现,以提高运算速度,节约重复运算成本。
首先,单个滑动窗口区域进入CNN网络模型时,包含全连接层。那么滑动窗口算法卷积实现的第一步就是将全连接层转变成为卷积层,如下图所示:
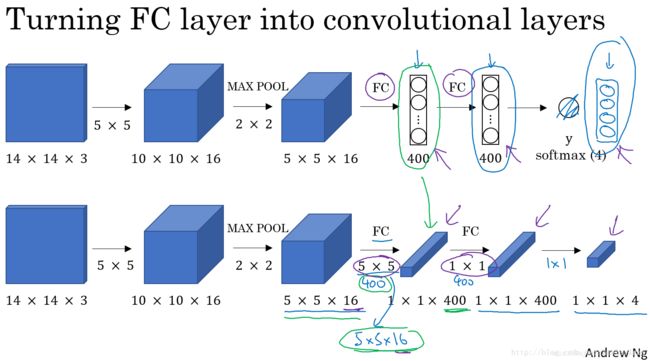
全连接层转变成卷积层的操作很简单,只需要使用与上层尺寸一致的滤波算子进行卷积运算即可。最终得到的输出层维度是1x1x4,代表4类输出值。
单个窗口区域卷积解结构建立完成后,对于待检测图片,即可使用该网络参数和结构进行运算。例如16x16x3的图片,步进长度为2,卷积核大小为单个窗口区域大小,CNN网络得到的输出层为2x2x4。其中,2x2表示共有4个窗口结果。对于更复杂的28x28x3的图片,CNN网络得到的输出层为8x8x4,共64个窗口结果。
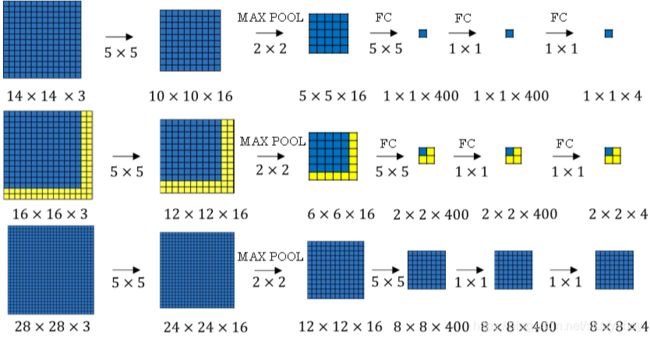

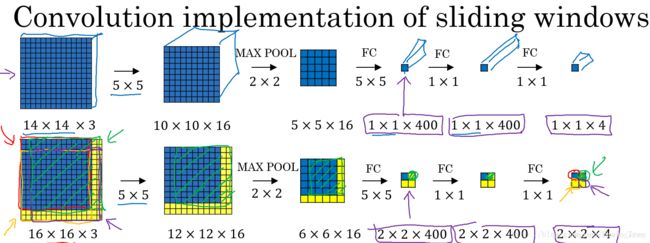
之前的滑动窗口算法需要反复进行CNN正向计算,例如16x16x3的图片需要进行4次,28x28x3的图片需要进行64次。而利用卷积操作代替滑动窗口算法,则不管原始图片有多大,只需要进行一次CNN正向计算,因为其中共享了很多重复计算部分,这大大节约了运算成本。窗口步进长度与选择的MaxPooling大小有关。如果需要步进长度为4,只需设置MaxPooling为4x4即可。
Bounding Box Predictions
滑动窗口算法有时会出现滑动窗不能完全涵盖目标的问题,如下图蓝色窗口所示。YOLO(You Only Look Once)算法可以解决这类问题,生成更加准确的目标区域(如下图红色窗口)。

YOLO算法首先将原始图片分割成n x n网格,每个网格代表一块区域。为简化说明,下图中将图片分成3 x 3网格。
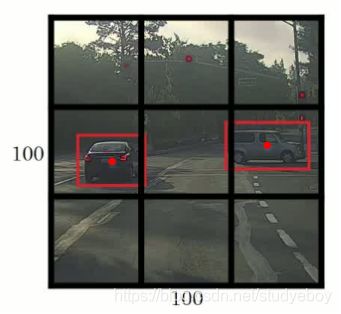
然后,利用上一节卷积形式实现滑动窗口算法的思想,对该原始图片构建CNN网络,得到的的输出层维度为3 x 3 x 8。其中,3 x 3对应9个网格,每个网格的输出包含8个元素:
y = [ P c b x b y b h b w c 1 c 2 c 3 ] (3) y=\left [ \begin{matrix} P_c \\ b_x \\ b_y \\ b_h \\ b_w \\ c_1 \\ c_2 \\ c_3 \end{matrix} \right ] \tag{3} y=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡Pcbxbybhbwc1c2c3⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤(3)
如果目标中心坐标 ( b x , b y ) (b_x, b_y) (bx,by)不在当前网格内,则当前网格 P c = 0 P_c=0 Pc=0;相反,则当前网格 P c = 1 P_c=1 Pc=1(即只看中心坐标是否在当前网格内)。判断有目标的网格中, b x , b y , b h , b w b_x, b_y, b_h, b_w bx,by,bh,bw限定了目标区域。当前网格左上角坐标设定为(0,0),右下角坐标设定为(1,1), ( b x , b y ) (b_x, b_y) (bx,by)范围限定在[0,1]之间,但是 b h , b w b_h, b_w bh,bw可以大于1。因为目标可能超出该网格,横跨多个区域,目标占几个网格没有关系,目标中心坐标必然在一个网格之内。
划分的网格可以更密一些,网格越小,则多个目标的中心坐标被划分到一个网络内的概率就越小。
Intersection Over Union
IoU,即交集与并集之比,可以用来评价目标检测区域的准确性。
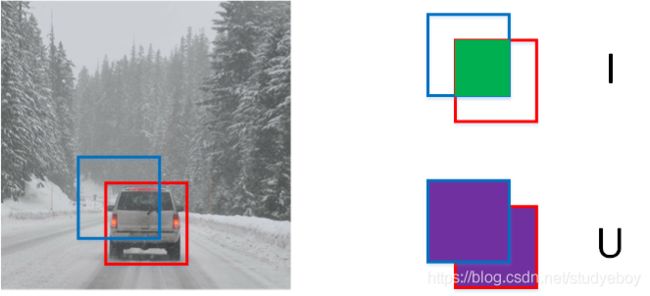
如上图所示,红色方框为真实目标区域,蓝色方框为检测目标区域。两块区域的交集为绿色部分,并集为紫色部分。蓝色方框与红色方框的接近程度可以用IoU比值来定义:
I o U = I U IoU = \frac{I}{U} IoU=UI
IoU可以表示任意两块区域的接近程度。IoU值介于0~1之间,且越接近1表示两块区域越接近。
非最大值抑制(non-max suppression,NMS)
YOLO算法汇总,可能会出现多个网格都检测到同一目标的情况,例如几个相邻网格都判断出同一目标的中心坐标在其内。下图中,三个绿色网格和三个红色网格分别检测的都是同一目标。判断哪个网格最为准确,使用非极大值抑制算法。

非极大值抑制(Non-max Suppression)做法很简单,下图所示,每个网格的 P c P_c Pc值可以求出, P c P_c Pc值反映了该网格包含目标中心坐标的可信度。首先选取 P c P_c Pc最大值对应的网格和区域,然后计算该区域与所有其它区域的IoU,剔除掉IoU大于阈值(例如0.5)的所有网格及区域。这样就能保证同一目标只有一个网格与之对应,且该网格 P c P_c Pc最大,最可信。然后再从剩下网格中选取 P c P_c Pc最大的网格,重复上一步的操作。最后就能是得每个目标都能仅由一个网格和区域对应。如下图示所示。
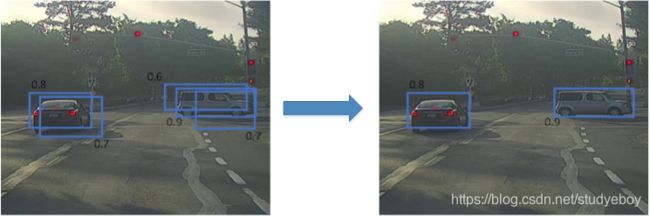
非极大值抑制算法流程:
- 步骤1,对图像每个网格预测,输出矩阵中包含表示有对象的概率 P c P_c Pc;
- 步骤2,剔除 P c P_c Pc值小于某阈值(例如0.6)的所有网格;
- 步骤3,对剩余的网格,选取 P c P_c Pc值最大的网格,抛弃和选取的网格 I o U ≥ 0.5 IoU \geq 0.5 IoU≥0.5的网格;
- 步骤4,对剩下的网格,重复步骤3
Anchor Boxes
前面介绍的都是一个网格至多只能检测一个目标,对于多个目标重叠的情况,例如一个人站在一辆车前面,该情况下使用YOLO算法进行检测,需要使用不同形状的Anchor Boxes。
如下图所示,同一个网格出现了两个目标:为了同时检测两个目标,可以设置两个Anchor Boxes,Anchor Box1检测人,Anchor Box2检测车。即每个网格多加了一层输出。原来的输出维度是3x3x8,现在的输出维度是3x3x2x8(也可以写成3x3x16的形式)。这里的2表示两个Anchor Boxes,用来在一个网格中同时检测多个目标。每个Anchor Box都有一个 P c P_c Pc值,若两个 P c P_c Pc值均大于某阈值,则检测到了两个目标。
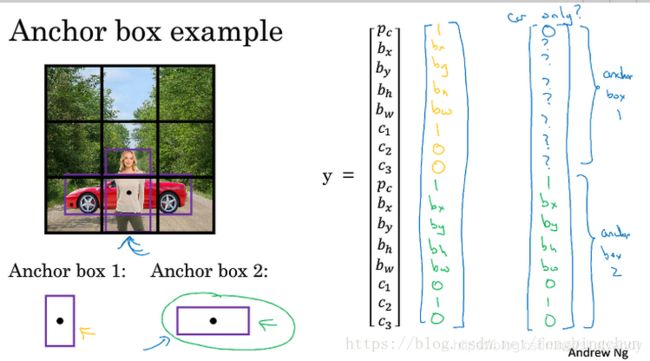
在使用YOLO算法时,只需对每个Anchor Box使用非极大值抑制即可,Anchor Boxes之间并行实现。Anchor Boxes处理不好的情况:
- 一个格子中出现三个及以上的物体
- 一个格子中两个物体的anchor boxes形状相似
Anchor Boxes形状的选择可以通过人为选取,选择5-10个以覆盖到多种不同的形状,可以涵盖想要检测的对象的形状;也可以使用其他机器学习算法,例如k剧烈算法对待检测的所有目标进行形状分类,选择主要形状作为Anchor Boxes。
YOLO算法(YOLO Algorithm)
假设要在图片中检测行人、汽车、摩托车三种目标,同时使用两种不同的Anchor Boxes。
训练集
- 输入X:同样大小的完整图片;
- 目标Y:使用3x3网格划分,输出大小3x3x2x8,或者3x3x16;
- 对不同格子中的小图,定义目标输出向量Y。
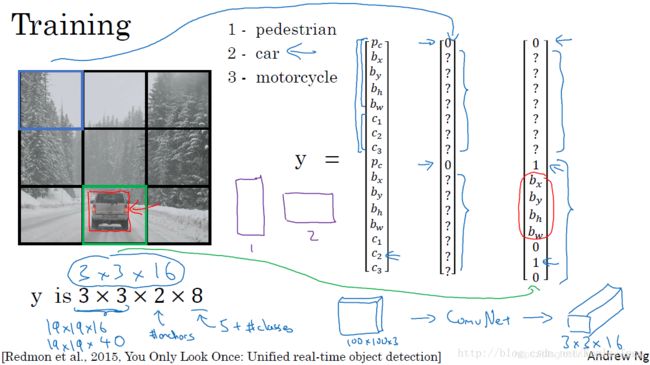
模型预测
输入与训练集中相同大小的图片,同时得到每个格子中不同的输出结果:3x3x2x8。

非极大值抑制
假设使用了2个Anchor Box,那么对于每一个网格,都会得到预测输出的2个bounding boxes,其中一个 P c P_c Pc比较高。

抛弃概率 P c P_c Pc值低的预测bounding boxes。

对每个对象(如行人、汽车、摩托车)分别使用NMS算法得到最终的预测边界框。

候选区域(Region Proposals)
滑动窗算法会对原始图片的每个区域都进行扫描,即使是一些空白的或明显没有目标的区域,例如下图所示。这样会降低算法运行效率,耗费时间。

为了解决这一问题,尽量避免对无用区域的扫描,可以使用Region Proposals的方法。具体做法是先对原始图片进行分割算法处理,将图片分割成许多不同颜色的色块,然后只对分割后的图片中的块进行目标检测。
- R-CNN:给出候选区域,对每个候选区域进行分类识别,输出对象标签和bounding box,从而在确实存在对象的区域得到更精确的边界框,滑动窗的形式,一次只对单个区域块进行目标检测,运算速度慢。
- Fast R-CNN:给出候选区域,使用滑动窗口的卷积实现取分类所有的候选区域,但得到候选区的聚类步骤仍然非常慢。
- Faster R-CNN:使用卷积网络给出候选区域,利用卷积对图片进行分割,进一步提高运行速度。
人脸识别
什么是人脸识别(What is face recognition)
人脸验证(face verification)和人脸识别(face recognition)的区别。
- 人脸验证:输入一张人脸图片,验证输出与模板是否为同一人,即一对一问题。
- 人脸识别:输入一张人脸图片,验证输出是否为K个模板中的某一个,即一对多问题。
一般地,人脸识别比人脸验证更难一些。因为假设人脸验证系统的错误率是1%,那么在人脸识别中,输出分别与K个模板都进行比较,则相应的错误率就会增加,约K%。模板个数越多,错误率越大一些。
One Shot Learning
One-shot learning就是说数据库中每个人的训练样本只包含一张照片,然后训练一个CNN模型来进行人脸识别。若数据库有K个人,则CNN模型输出softmax层就是K维的。
one-shot learning的性能不好,存了两个缺点:
- 每个人只有一张照片,训练样本少,构建的CNN网络不够健壮;
- 若数据库增加另一个人,输出层softmax的维度就要发生变化,相当于要重新构建CNN网络,使模型计算量增加,不够灵活。
为了解决one-shot learning问题,先介绍相似函数(similarity function)。相似函数表示两张图片的相似程度,用d(img1,img2)来表示。若d(img1,img2)较小,则表示两张图片相似;若d(img1,img2)较大,则表示两张图片不是同一个人。相似函数可以在人脸验证中使用:
- d ( i m g 1 , i m g 2 ) ≤ τ d(img1,img2)\leq \tau d(img1,img2)≤τ:一样
- d ( i m g 1 , i m g 2 ) > τ d(img1,img2)>τ d(img1,img2)>τ : 不一样
对于人脸识别问题,则只需计算测试图片与数据库中K个目标的相似函数,取其中d(img1,img2)最小的目标为匹配对象。若所有的d(img1,img2)都很大,则表示数据库中没有这个人。

Siamese Network
若一张图片经过一般的CNN网络(包括CONV层、POOL层、FC层),最终得到全连接层FC,该FC层可以看成是原始图片的编码encoding,表征了原始图片的关键特征。这个网络结构我们称之为Siamese network。也就是说每张图片经过Siamese network后,由FC层每个神经元来表征。
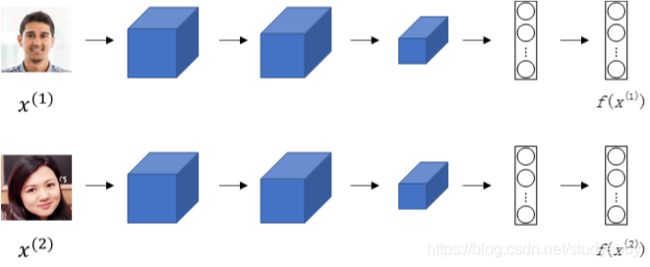

Triplet Loss
构建人脸识别的CNN模型,需要定义合适的损失函数,这里使用Triplet Loss。
Triplet Loss需要每个样本包含三张图片:靶目标(Anchor)、正例(Positive)、反例(Negative),这就是triplet名称的由来。顾名思义,靶目标和正例是同一人,靶目标和反例不是同一人。Anchor和Positive组成一类样本,Anchor和Negative组成另外一类样本。




所以,最好的做法是人为选择A与P相差较大(例如换发型,留胡须等),A与N相差较小(例如发型一致,肤色一致等)。这种人为地增加难度和混淆度会让模型本身去寻找学习不同人脸之间关键的差异,“尽力”让d(A,P)d(A,P)更小,让d(A,N)d(A,N)更大,即让模型性能更好。
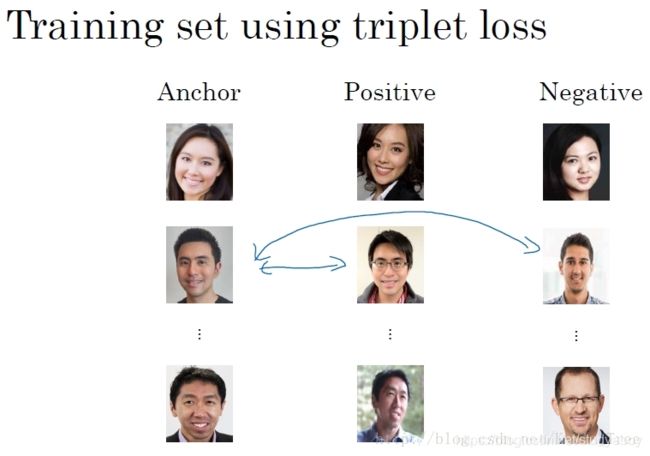
脸部验证和二分类(Face Verification and Binary Classification)
除了构造triplet loss来解决人脸识别问题之外,还可以使用二分类结构。做法是将两个siamese网络组合在一起,将各自的编码层输出经过一个逻辑输出单元,该神经元使用sigmoid函数,输出1则表示识别为同一人,输出0则表示识别为不同人。结构如下:


风格迁移
什么是风格迁移(What is neural style transfer)
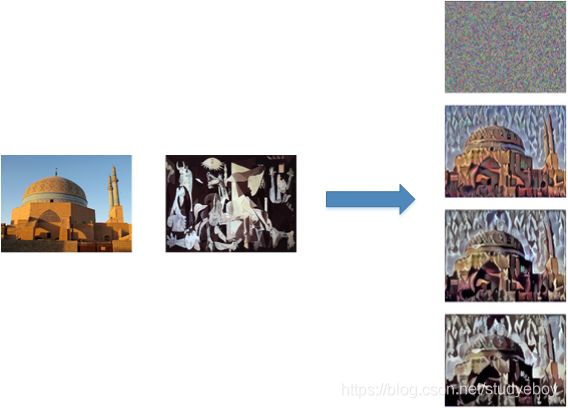
神经风格迁移是CNN模型一个非常有趣的应用。它可以实现将一张图片的风格“迁移”到另外一张图片中,生成具有其特色的图片。
What are deep ConvNets learning
在进行神经风格迁移之前,我们先来从可视化的角度看一下卷积神经网络每一层到底是什么样子?它们各自学习了哪些东西。
典型的CNN网络如下所示:

首先,遍历所有训练样本,找出让第一层隐藏层激活函数输出最大的9块图像区域;然后再找出该层的其它单元(不同的滤波器通道)激活函数输出最大的9块图像区域;最后共找9次,得到9x9的图像如下所示,其中每个3x3区域表示一个运算单元。
![]()
可以看出,第一层隐藏层一般检测的是原始图像的边缘和颜色阴影等简单信息。
随着层数的增加,CNN更深,捕捉的区域更大,特征更加复杂,从边缘到纹理再到具体物体。

Cost Function
一般用C表示内容图片,S表示风格图片,G表示生成的图片。
神经风格迁移生成图片G的cost function由两部分组成:C与G的相似程度和S与G的相似程度。
J ( G ) = α ⋅ J c o n t e n t ( C , G ) + β ⋅ J s t y l e ( S , G ) J(G)=\alpha \cdot J_{content}(C,G)+\beta \cdot J_{style}(S,G) J(G)=α⋅Jcontent(C,G)+β⋅Jstyle(S,G)
- α , β α,β α,β是超参数,用来调整 J c o n t e n t ( C , G ) J_{content}(C,G) Jcontent(C,G)与 J s t y l e ( S , G ) J_{style}(S,G) Jstyle(S,G)的相对比重。
- J c o n t e n t ( C , G ) J_{content}(C,G) Jcontent(C,G)表示生成图片和G的内容和内容图片C的内容的相似度。
- J s t y l e ( S , G ) J_{style}(S,G) Jstyle(S,G)表示生成图片G的内容和风格图片S的内容的相似度。
风格迁移的算法流程:
- 随机初始化生成图片G。
- 使用梯度下降算法,不断修正G的所有像素点,使得 J ( G ) J(G) J(G)不断减小,从而使G逐渐具有C的内容和S的风格。
内容代价函数(Content Cost Function)
风格代价函数(Style Cost Function)
什么是图片的风格?利用CNN网络模型,图片的风格可以定义成第l层隐藏层不同通道间激活函数的乘积(相关性)。

例如我们选取第ll层隐藏层,其各通道使用不同颜色标注,如下图所示。因为每个通道提取图片的特征不同,比如1通道(红色)提取的是图片的垂直纹理特征,2通道(黄色)提取的是图片的橙色背景特征。那么计算这两个通道的相关性大小,相关性越大,表示原始图片及既包含了垂直纹理也包含了该橙色背景;相关性越小,表示原始图片并没有同时包含这两个特征。也就是说,计算不同通道的相关性,反映了原始图片特征间的相互关系,从某种程度上刻画了图片的“风格”。
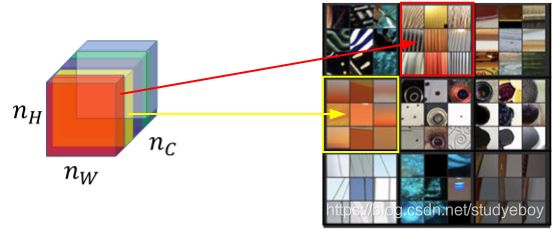

1D and 3D Generalizations
在我们上面学过的卷积中,多数是对图形应用2D的卷积运算。同时,我们所应用的卷积运算还可以推广到1D和3D的情况。


序列模型
循环神经网络
序列模型的应用(Why sequence models)
- 语音识别:将输入的语音信号直接输出相应的语音文本信息。无论语音信号还是文本信息均是序列数据。
- 音乐生成:生成音乐乐谱。只有输出的音乐乐谱是序列数据,输入可以是空或者一个整数。
- 情感分类:将输入的评论句子转换为相应的等级或评分。输入是一个序列,输出则是一个单独的类别。
- DNA序列分析:找到输入的DNA序列的蛋白质表达的子序列。
- 机器翻译:两种不同语言之间的想换转换。输入和输出均为序列数据。
- 视频行为识别:识别输入的视频帧序列中的人物行为。
- 命名实体识别:从输入的句子中识别实体的名字。

这些序列模型基本都属于监督式学习,输入x和输出y不一定都是序列模型。如果都是序列模型的话,模型长度不一定完全一致。
命名规则(Notation)
循环神经网络模型(Recurrent Neural Network Model)
对于序列模型,如果使用标准的神经网络,其模型结构如下:


标准的神经网络不适合解决序列模型问题,而循环神经网络(RNN)是专门用来解决序列模型问题的。RNN模型结构如下:




穿越时间的反向传播(Backpropagation through time)
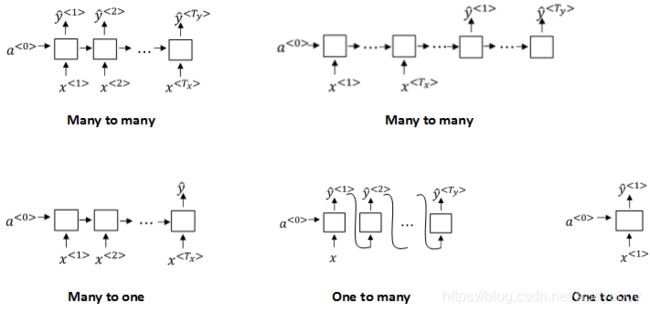
不同类型的RNN(Different types of RNNs)
语言模型和序列生成(Language model and sequence generation)
语言模型是自然语言处理(NLP)中最基本和最重要的任务之一。使用RNN能够很好地建立需要的不同语言风格的语言模型。

准备好训练集并对语料库进行切分词等处理之后,接下来构建相应的RNN模型。


新序列采样(Sampling novel sequences)
利用训练好的RNN语言模型,可以进行新的序列采样,从而随机产生新的语句。相应的RNN模型如下所示:


RNN的梯度消失(Vanisging gradients with RNNs)
Gated Recurrent Unit(GRU)
RNN的隐藏层单元结构如下图所示:
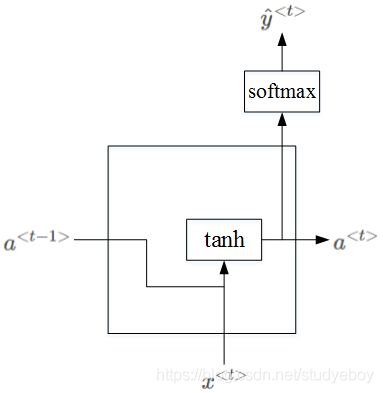
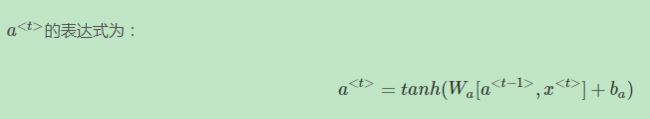
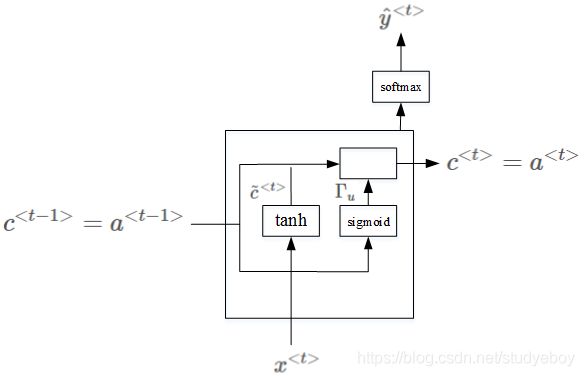
为了解决梯度消失问题,对上述单元进行修改,添加了记忆单元,构建GRU,如下图所示:


Long Short Term Memory(LSTM)
LSTM是另一种更强大的解决梯度消失问题的方法。它对应的RNN隐藏层单元结构如下图所示:



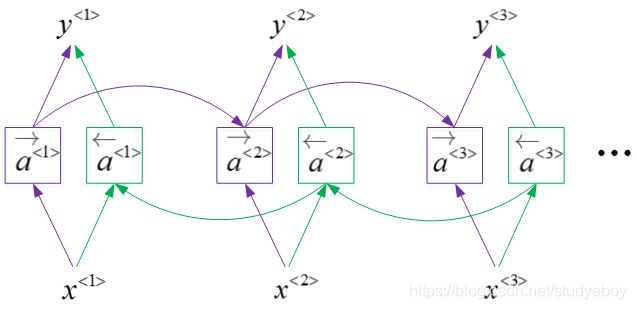
双向RNN(Bidirectional RNN)
双向RNN(bidirectional RNNs)模型能够让我们在序列的某处,不仅可以获取之间的信息,还可以获取未来的信息。
Deep RNNs
Deep RNNs由多层RNN组成,其结构如下图所示:
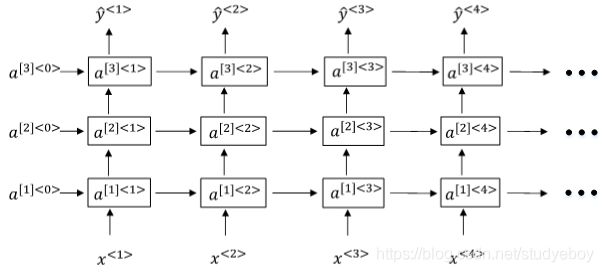

另外一种Deep RNNs结构是每个输出层上还有一些垂直单元,如下图所示:
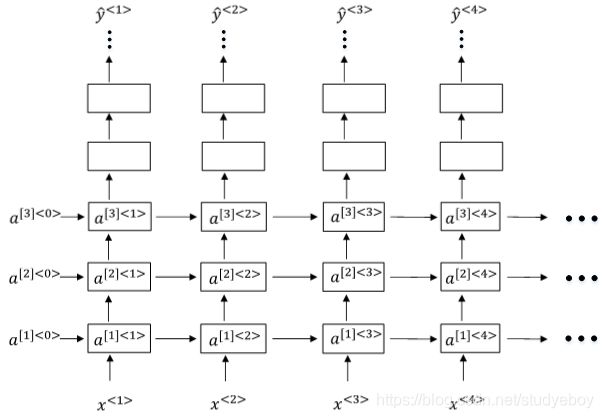
自然语言处理和词嵌入
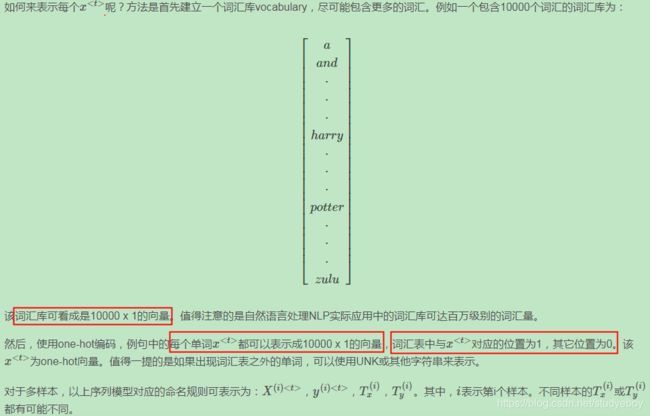
词汇表征(Word Representation)
表征单词的方式是首先建立一个较大的词汇表(例如10000),然后使用one-hot的方式对每个单词进行编码。例如单词Man,Woman,King,Queen,Apple,Orange分别出现在词汇表的第5391,9853,4914,7157,456,6257的位置,则它们分别用 O 5391 O_{5391} O5391, O 9853 O_{9853} O9853, O 4914 O_{4914} O4914, O 7157 O_{7157} O7157, O 456 O_{456} O456, O 6257 O_{6257} O6257, O 5391 O_{5391} O5391, O 9853 O_{9853} O9853, O 4914 O_{4914} O4914, O 7157 O_{7157} O7157, O 456 O_{456} O456, O 6257 O_{6257} O6257表示。

这中one-hot表征单词的方法最大的缺点就是每个单词都是独立的、正交的,无法知道不同单词之间的相似程度。例如Apple和Orange都是水果,词性相近,但是单从one-hot编码上来看,内积为零,无法知道二者的相似性。在NLP中,我们更希望能掌握不同单词之间的相似程度。
因此,我们可以使用特征表征(Featurized representation)的方法对每个单词进行编码。也就是使用一个特征向量表征单词,特征向量的每个元素都是对该单词某一特征的量化描述,量化范围可以是[-1,1]之间。特征表征的例子如下图所示:
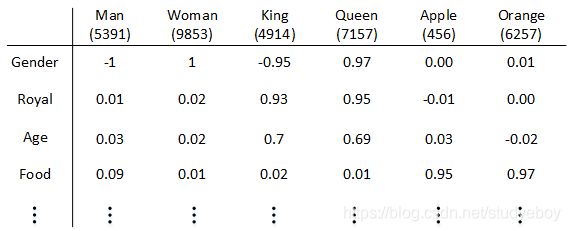
特征向量的长度依情况而定,特征元素越多则对单词表征得越全面。这里的特征向量长度设定为300。使用特征表征之后,词汇表中的每个单词都可以使用对应的300 x 1的向量来表示,该向量的每个元素表示该单词对应的某个特征值。每个单词用e+词汇表索引的方式标记,例如 e 5391 e_{5391} e5391, e 9853 e_{9853} e9853, e 4914 e_{4914} e4914, e 7157 e_{7157} e7157, e 456 e_{456} e456, e 6257 e_{6257} e6257, e 5391 e_{5391} e5391, e 9853 e_{9853} e9853, e 4914 e_{4914} e4914, e 7157 e_{7157} e7157, e 456 e_{456} e456, e 6257 e_{6257} e6257。
这种特征表征的优点是根据特征向量能清晰知道不同单词之间的相似程度,例如Apple和Orange之间的相似度较高,很可能属于同一类别。这种单词“类别”化的方式,大大提高了有限词汇量的泛化能力。这种特征化单词的操作被称为Word Embeddings,即单词嵌入。
这里特征向量的每个特征元素含义是具体的,对应到实际特征,例如性别、年龄等。而在实际应用中,特征向量很多特征元素并不一定对应到有物理意义的特征,是比较抽象的。但是,这并不影响对每个单词的有效表征,同样能比较不同单词之间的相似性。
每个单词都由高维特征向量表征,为了可视化不同单词之间的相似性,可以使用降维操作,例如t-SNE算法,将300D降到2D平面上。如下图所示:
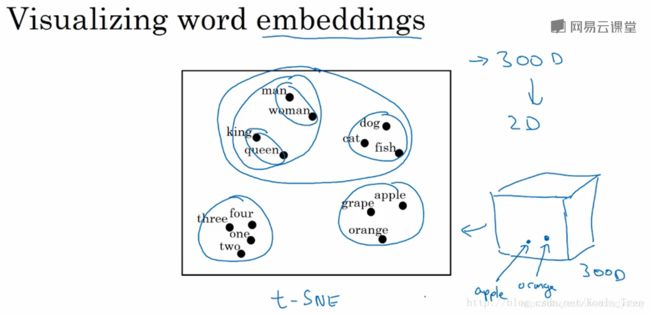
从上图可以看出相似的单词分布距离较近,从而也证明了Word Embeddings能有效表征单词的关键特征。
使用词嵌入(Using word embedding)
Word Embeddings对不同单词进行了实现了特征化的表示,那么如何将这种表示方法应用到自然语言处理的应用中呢?
名字实体识别的例子
如下面的一个句子中名字实体的定位识别问题,假如我们有一个比较小的数据集,可能不包含durain(榴莲)和cultivator(培育家)这样的词汇,那么我们就很难从包含这两个词汇的句子中识别名字实体。但是如果我们从网上的其他地方获取了一个学习好的word Embedding,它将告诉我们榴莲是一种水果,并且培育家和农民相似,那么我们就有可能从我们少量的训练集中,归纳出没有见过的词汇中的名字实体。
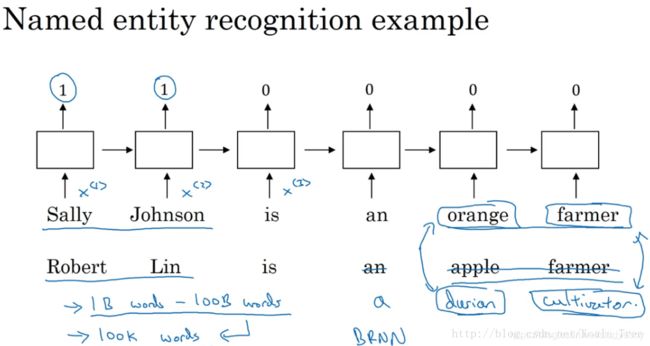
可以看出,featurized representation的优点是可以减少训练样本的数目,前提是对海量单词建立特征向量表述(word embedding)。这样,即使训练样本不够多,测试时遇到陌生单词,例如“durian cultivator”,根据之前海量词汇特征向量就判断出“durian”也是一种水果,与“apple”类似,而“cultivator”与“farmer”也很相似。从而得到与“durian cultivator”对应的应该也是一个人名。这种做法将单词用不同的特征来表示,即使是训练样本中没有的单词,也可以根据word embedding的结果得到与其词性相近的单词,从而得到与该单词相近的结果,有效减少了训练样本的数量。
词嵌入的迁移学习
featurized representation的特性使得很多NLP任务能方便地进行迁移学习。方法是:
- 从海量词汇库中学习word embeddings,即所有单词的特征向量。或者从网上下载预训练好的word embeddings。
- 使用较少的训练样本,将word embeddings迁移到新的任务中。
- (可选):继续使用新数据微调word embeddings。
建议仅当训练样本足够大的时候,再进行上述第三步。
词嵌入和人脸编码
词嵌入和人脸编码之间有很奇妙的联系。在人脸识别领域,我们会将人脸图片预编码成不同的编码向量,以表示不同的人脸,进而在识别的过程中使用编码来进行比对识别。词嵌入则和人脸编码有一定的相似性。
人脸图片经过Siamese网络,得到其特征向量f(x),这点跟word embedding是类似的。二者不同的是Siamese网络输入的人脸图片可以是数据库之外的;而word embedding一般都是已建立的词汇库中的单词,非词汇库单词统一用< UNK >表示。
词嵌入的特性(Properties of word embeddings)
Word embeddings可以帮助我们找到不同单词之间的相似类别关系。如下图所示:
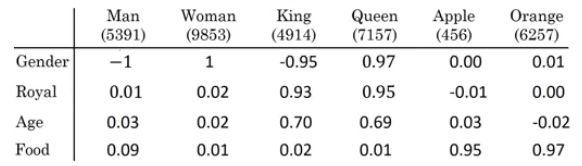
上例中,特征维度是4维的,分别是[Gender, Royal, Age, Food]。常识地,“Man”与“Woman”的关系类比于“King”与“Queen”的关系。而利用Word embeddings可以找到这样的对应类比关系。

一般地,A类比于B相当于C类比于“?”,这类问题可以使用embedding vector进行运算。


嵌入矩阵(Embedding matrix)
在我们要对一个词汇表学习词嵌入模型时,实质上就是要学习这个词汇表对应的一个嵌入矩阵E。当我们学习好了这样一个嵌入矩阵后,通过嵌入矩阵与对应词的one-hot向量相乘,则可得到该词汇的embedding,如下图所示:
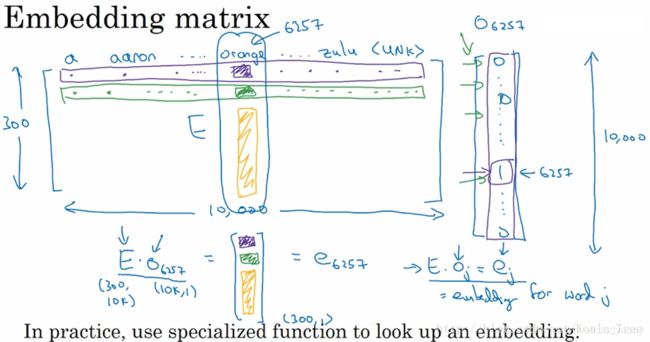

学习词嵌入(Learning word embeddings)
Word2Vec
Word2Vec算法是一种简单的计算更加高效的方式来实现对词嵌入的学习。比较流行的是采用Skip-Gram模型。以下面这句话为例:
负采样(Negative Sampling)
GloVe word vectors
GloVe(global vectors for word representation)词向量模型是另外一种计算词嵌入的方法,虽然相比下没有Skip-grams模型用的多,但是相比这种模型却更加简单。

情感分类(Sentiment Classification)
情感分类一般是根据一句话来判断其喜爱程度,例如1~5星分布。如下图所示:

情感分类问题的一个主要挑战是缺少足够多的训练样本。而Word embedding恰恰可以帮助解决训练样本不足的问题。
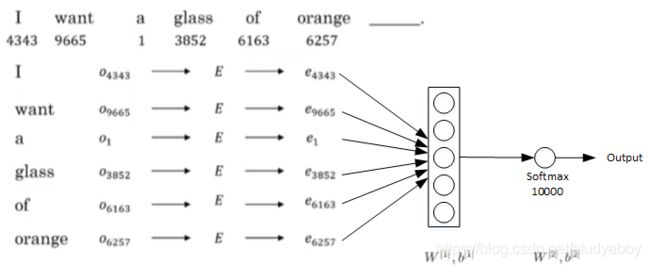
首先介绍使用word embedding解决情感分类问题的一个简单模型算法。

如上图所示,这句话的4个单词分别用embedding vector表示。 e 8928 e_{8928} e8928, e 2468 e_{2468} e2468, e 4694 e_{4694} e4694, e 3180 e_{3180} e3180, e 8928 e_{8928} e8928, e 2468 e_{2468} e2468, e 4694 e_{4694} e4694, e 3180 e_{3180} e3180计算均值,这样得到的平均向量的维度仍是300。最后经过softmax输出1~5星。这种模型结构简单,计算量不大,不论句子长度多长,都使用平均的方式得到300D的embedding vector。该模型实际表现较好。
但是,这种简单模型的缺点是使用平均方法,没有考虑句子中单词出现的次序,忽略其位置信息。而有时候,不同单词出现的次序直接决定了句意,即情感分类的结果。例如下面这句话:
Completely lacking in good taste, good service, and good ambience.
虽然这句话中包含了3个“good”,但是其前面出现了“lacking”,很明显这句话句意是negative的。如果使用上面介绍的平均算法,则很可能会错误识别为positive的,因为忽略了单词出现的次序。
为了解决这一问题,情感分类的另一种模型是RNN。
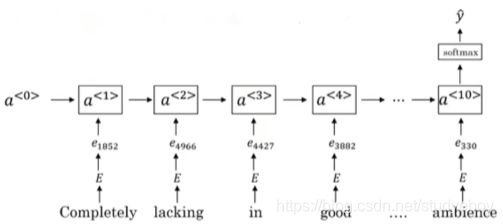
该RNN模型是典型的many-to-one模型,考虑单词出现的次序,能够有效识别句子表达的真实情感。
使用word embedding,能够有效提高模型的泛化能力,即使训练样本不多,也能保证模型有不错的性能。
词嵌入消除偏见(Debiasing word embeddings)
Word embeddings中存在一些性别、宗教、种族等偏见或者歧视。例如下面这两句话:
- Man: Woman as King: Queen
- Man: Computer programmer as Woman: Homemaker
- Father: Doctor as Mother: Nurse
很明显,第二句话和第三句话存在性别偏见,因为Woman和Mother也可以是Computer programmer和Doctor。
以性别偏见为例,我们来探讨下如何消除word embeddings中偏见。
- 首先,确定偏见bias的方向。方法是对所有性别对立的单词求差值,再平均。下图展示了bias direction和non-bias direction。
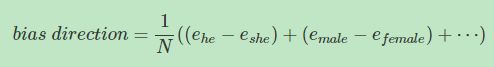
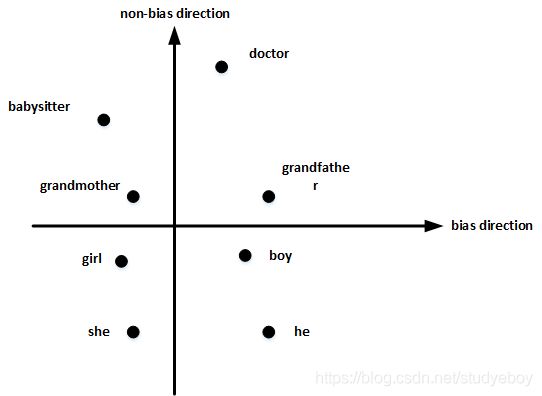
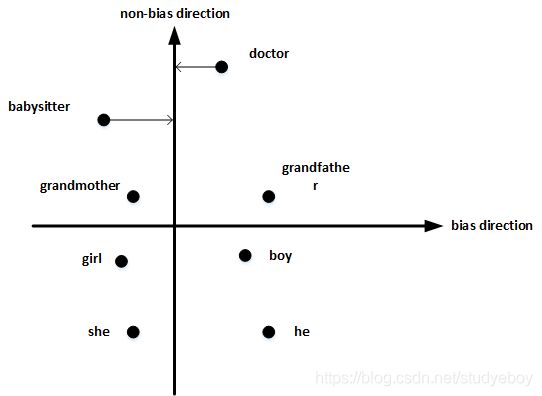
- 然后,单词中立化(Neutralize)。将需要消除性别偏见的单词投影到non-bias direction上去,消除bias维度,例如babysitter,doctor等。
- 最后,均衡对(Equalize pairs)。让性别对立单词与上面的中立词距离相等,具有同样的相似度。例如让grandmother和grandfather与babysitter的距离同一化。
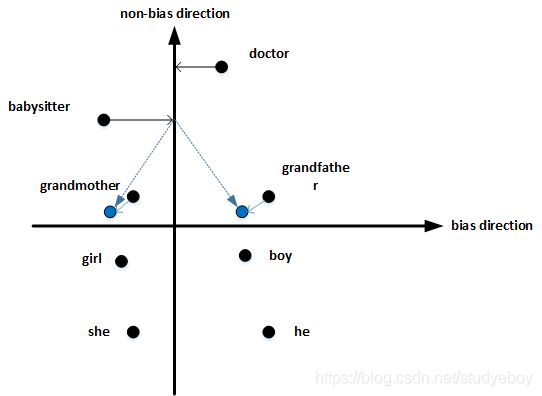
值得注意的是,掌握哪些单词需要中立化非常重要。一般来说,大部分英文单词,例如职业、身份等都需要中立化,消除embedding vector中性别这一维度的影响。
序列模型和注意力机制
基础模型(Basic Models)
sequence to sequence 模型最为常见的就是机器翻译,假如这里我们要将法语翻译成英文:

针对该机器翻译问题,可以使用“编码网络(encoder network)”+“解码网络(decoder network)”两个RNN模型组合的形式来解决。encoder network将输入语句编码为一个特征向量,传递给decoder network,完成翻译。具体模型结构如下图所示:
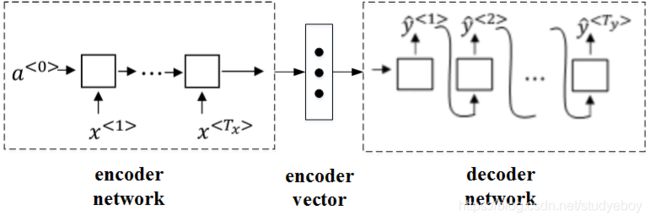
其中,encoder vector代表了输入语句的编码特征。encoder network和decoder network都是RNN模型,可使用GRU或LSTM单元。这种“编码网络(encoder network)”+“解码网络(decoder network)”的模型,在实际的机器翻译应用中有着不错的效果。
这种模型也可以应用到图像捕捉领域。图像捕捉,即捕捉图像中主体动作和行为,描述图像内容。例如下面这个例子,根据图像,捕捉图像内容。

首先,可以将图片输入到CNN,例如使用预训练好的AlexNet,删去最后的softmax层,保留至最后的全连接层。则该全连接层就构成了一个图片的特征向量(编码向量),表征了图片特征信息。
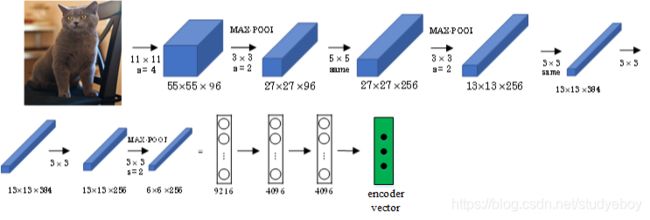
然后,将encoder vector输入至RNN,即decoder network中,进行解码翻译。

挑选最可能的句子(Picking the most likely sentence)
Sequence to sequence machine translation模型与我们第一节课介绍的language模型有一些相似,但也存在不同之处。二者模型结构如下所示:
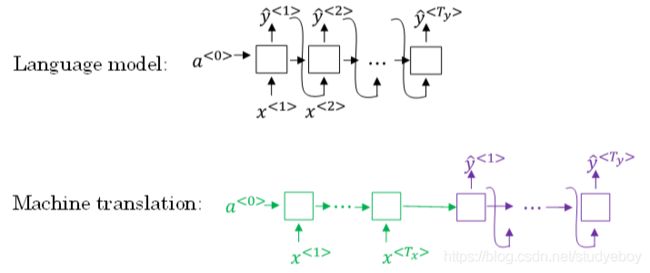
Language model是自动生成一条完整语句,语句是随机的。而machine translation model是根据输入语句,进行翻译,生成另外一条完整语句。上图中,绿色部分表示encoder network,紫色部分表示decoder network。decoder network与language model是相似的,encoder network可以看成是language model的 a < 0 > a^{<0>} a<0>,是模型的一个条件。也就是说,在输入语句的条件下,生成正确的翻译语句。因此,machine translation可以看成是有条件的语言模型(conditional language model)。这就是二者之间的区别与联系。
所以,machine translation的目标就是根据输入语句,作为条件,找到最佳翻译语句,使其概率最大:

例如,模型可能得到的几个翻译:

显然,第一条翻译“Jane is visiting Africa in September.”最为准确。那我们的优化目标就是要让这条翻译对应的 P ( y < 1 > , ⋯ , y < T y > ∣ x ) P(y^{<1>},⋯,y^{
实现优化目标的方法之一是使用贪婪搜索(greedy search)。Greedy search根据条件,每次只寻找一个最佳单词作为翻译输出,力求把每个单词都翻译准确。例如,首先根据输入语句,找到第一个翻译的单词“Jane”,然后再找第二个单词“is”,再继续找第三个单词“visiting”,以此类推。这也是其“贪婪”名称的由来。
Greedy search存在一些缺点。首先,因为greedy search每次只搜索一个单词,没有考虑该单词前后关系,概率选择上有可能会出错。例如,上面翻译语句中,第三个单词“going”比“visiting”更常见,模型很可能会错误地选择了“going”,而错失最佳翻译语句。其次,greedy search大大增加了运算成本,降低运算速度。
因此,greedy search并不是最佳的方法。
集束搜索(Beam Search)
Beam Search,使用近似最优的查找方式,最大化输出概率,寻找最佳的翻译语句。
Greedy search每次是找出预测概率最大的单词,而beam search则是每次找出预测概率最大的B个单词。其中,参数B表示取概率最大的单词个数,可调。本例中,令B=3。
按照beam search的搜索原理,首先,先从词汇表中找出翻译的第一个单词概率最大的B个预测单词。例如上面的例子中,预测得到的第一个单词为:in,jane,september。
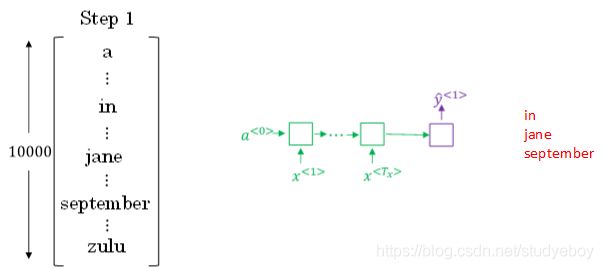
概率表示为: P ( y ^ < 1 > ∣ x ) P(\hat y^{<1>}|x) P(y^<1>∣x)
然后,再分别以in,jane,september为条件,计算每个词汇表单词作为预测第二个单词的概率。从中选择概率最大的3个作为第二个单词的预测值,得到:in september,jane is,jane visits。
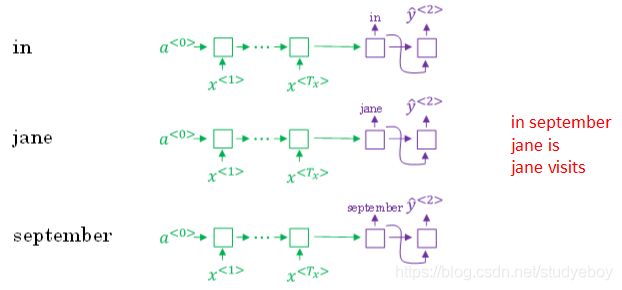
概率表示为: P ( y ^ < 2 > ∣ x , y ^ < 1 > ) P(\hat y^{<2>}|x,\hat y^{<1>}) P(y^<2>∣x,y^<1>)。
此时,得到的前两个单词的3种情况的概率为:
P ( y ^ < 1 > , y ^ < 2 > ∣ x ) = P ( y ^ < 1 > ∣ x ) ⋅ P ( y ^ < 2 > ∣ x , y ^ < 1 > ) P(\hat y^{<1>},\hat y^{<2>}|x)=P(\hat y^{<1>}|x)⋅P(\hat y^{<2>}|x,\hat y^{<1>}) P(y^<1>,y^<2>∣x)=P(y^<1>∣x)⋅P(y^<2>∣x,y^<1>)
接着,再预测第三个单词。方法一样,分别以in september,jane is,jane visits为条件,计算每个词汇表单词作为预测第三个单词的概率。从中选择概率最大的3个作为第三个单词的预测值,得到:in september jane,jane is visiting,jane visits africa。
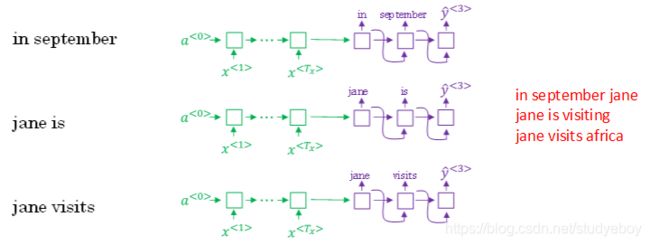
概率表示为: P ( y ^ < 3 > ∣ x , y ^ < 1 > , y ^ < 2 > ) P(\hat y^{<3>}|x,\hat y^{<1>},\hat y^{<2>}) P(y^<3>∣x,y^<1>,y^<2>)。
此时,得到的前三个单词的3种情况的概率为:
P ( y ^ < 1 > , y ^ < 2 > , y ^ < 3 > ∣ x ) = P ( y ^ < 1 > ∣ x ) ⋅ P ( y ^ < 2 > ∣ x , y ^ < 1 > ) ⋅ P ( y ^ < 3 > ∣ x , y ^ < 1 > , y ^ < 2 > ) P(\hat y^{<1>},\hat y^{<2>},\hat y^{<3>}|x)=P(\hat y^{<1>}|x)⋅P(\hat y^{<2>}|x,\hat y^{<1>})⋅P(\hat y^{<3>}|x,\hat y^{<1>},\hat y^{<2>}) P(y^<1>,y^<2>,y^<3>∣x)=P(y^<1>∣x)⋅P(y^<2>∣x,y^<1>)⋅P(y^<3>∣x,y^<1>,y^<2>)
以此类推,每次都取概率最大的三种预测。最后,选择概率最大的那一组作为最终的翻译语句。
Jane is visiting Africa in September.
值得注意的是,如果参数B=1,则就等同于greedy search。实际应用中,可以根据不同的需要设置B为不同的值。一般B越大,机器翻译越准确,但同时也会增加计算复杂度。
集束搜索的改进(Refinements to Beam Search)
Beam search中,最终机器翻译的概率是乘积的形式:
a r g m a x ∏ t = 1 T y P ( y ^ < t > ∣ x , y ^ < 1 > , ⋯ , y ^ < t − 1 > ) arg\ max\prod_{t=1}^{T_y} P(\hat y^{
多个概率相乘可能会使乘积结果很小,远小于1,造成数值下溢。为了解决这个问题,可以对上述乘积形式进行取对数log运算,即:
a r g m a x ∑ t = 1 T y l o g P ( y ^ < t > ∣ x , y ^ < 1 > , ⋯ , y ^ < t − 1 > ) arg\ max\sum_{t=1}^{T_y}log P(\hat y^{
因为取对数运算,将乘积转化为求和形式,避免了数值下溢,使得数据更加稳定有效。
这种概率表达式还存在一个问题,就是机器翻译的单词越多,乘积形式或求和形式得到的概率就越小,这样会造成模型倾向于选择单词数更少的翻译语句,使机器翻译受单词数目的影响,这显然是不太合适的。因此,一种改进方式是进行长度归一化,消除语句长度影响。
a r g m a x 1 T y ∑ t = 1 T y l o g P ( y ^ < t > ∣ x , y ^ < 1 > , ⋯ , y ^ < t − 1 > ) arg\ max\ \frac{1}{T_y}\sum_{t=1}^{T_y} logP(\hat y^{
实际应用中,通常会引入归一化因子 α α α:
a r g m a x 1 T y α ∑ t = 1 T y l o g P ( y ^ < t > ∣ x , y ^ < 1 > , ⋯ , y ^ < t − 1 > ) arg\ max\ \frac{1}{T_y^{\alpha}}\sum_{t=1}^{T_y}log P(\hat y^{
若 α = 1 α=1 α=1,则完全进行长度归一化;若 α = 0 α=0 α=0,则不进行长度归一化。一般令 α = 0.7 α=0.7 α=0.7,效果不错。
与BFS (Breadth First Search) 、DFS (Depth First Search)算法不同,beam search运算速度更快,但是并不保证一定能找到正确的翻译语句。
集束搜索的误差分析(Error analysis in beam search)
Beam search是一种近似搜索算法。实际应用中,如果机器翻译效果不好,需要通过错误分析,判断是RNN模型问题还是beam search算法问题。
一般来说,增加训练样本、增大beam search参数B都能提高准确率。但是,这种做法并不能得到我们期待的性能,且并不实际。
Bleu Score(optional)
使用bleu score,对机器翻译进行打分。
首先,对原语句建立人工翻译参考,一般有多个人工翻译(利用验证集或测试集)。例如下面这个例子Reference1和Reference2两个人工翻译都是正确的,作为参考。相应的机器翻译MT output如下所示:
- French: Le chat est sur le tapis.
- Reference 1: The cat is on the mat.
- Reference 2: There is a cat on the mat.
- MT output: the the the the the the the.
如上所示,机器翻译为“the the the the the the the.”,效果很差。Bleu Score的宗旨是机器翻译越接近参考的人工翻译,其得分越高,方法原理就是看机器翻译的各个单词是否出现在参考翻译中。
-
最简单的准确度评价方法是看机器翻译的每个单词是否出现在参考翻译中。显然,上述机器翻译的每个单词都出现在参考翻译里,准确率为77=177=1,其中,分母为机器翻译单词数目,分子为相应单词是否出现在参考翻译中。但是,这种方法很不科学,并不可取。
-
另外一种评价方法是看机器翻译单词出现在参考翻译单个语句中的次数,取最大次数。上述例子对应的准确率为2727,其中,分母为机器翻译单词数目,分子为相应单词出现在参考翻译中的次数(分子为2是因为“the”在参考1中出现了两次)。这种评价方法较为准确。
上述两种方法都是对单个单词进行评价。按照beam search的思想,另外一种更科学的打分方法是bleu score on bigrams,即同时对两个连续单词进行打分。仍然是上面那个翻译例子:
- French: Le chat est sur le tapis.
- Reference 1: The cat is on the mat.
- Reference 2: There is a cat on the mat.
- MT output: The cat the cat on the mat.
对MIT output进行分解,得到的bigrams及其出现在MIT output中的次数count为:
- the cat: 2
- cat the: 1
- cat on: 1
- on the: 1
- the mat: 1
然后,统计上述bigrams出现在参考翻译单个语句中的次数(取最大次数)countclipcountclip为:
- the cat: 1
- cat the: 0
- cat on: 1
- on the: 1
- the mat: 1
相应的bigrams precision为:
c o u n t c l i p c o u n t = 1 + 0 + 1 + 1 + 1 2 + 1 + 1 + 1 + 1 = 4 6 = 2 3 \frac{count_{clip}}{count}=\frac{1+0+1+1+1}{2+1+1+1+1}=\frac46=\frac23 countcountclip=2+1+1+1+11+0+1+1+1=64=32
如果只看单个单词,相应的unigrams precision为:
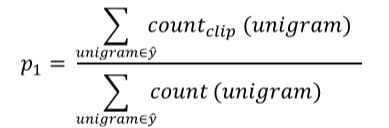
如果是n个连续单词,相应的n-grams precision为:
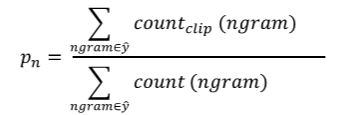
总结一下,可以同时计算 p 1 , ⋯ , p n p1,⋯,pn p1,⋯,pn,再对其求平均:
p = 1 n ∑ i = 1 n p i p=\frac1n\sum_{i=1}^np_i p=n1i=1∑npi
通常,对上式进行指数处理,并引入参数因子brevity penalty,记为BP。顾名思义,BP是为了“惩罚”机器翻译语句过短而造成的得分“虚高”的情况。
p = B P ⋅ e x p ( 1 n ∑ i = 1 n p i ) p=BP\cdot exp(\frac1n\sum_{i=1}^np_i) p=BP⋅exp(n1i=1∑npi)
注意力模型(Attention Model Intuition)
如果原语句很长,要对整个语句输入RNN的编码网络和解码网络进行翻译,则效果不佳。相应的bleu score会随着单词数目增加而逐渐降低。

对待长语句,正确的翻译方法是将长语句分段,每次只对长语句的一部分进行翻译。人工翻译也是采用这样的方法,高效准确。也就是说,每次翻译只注重一部分区域,这种方法使得bleu score不太受语句长度的影响。

根据这种“局部聚焦”的思想,建立相应的注意力模型(attention model)。
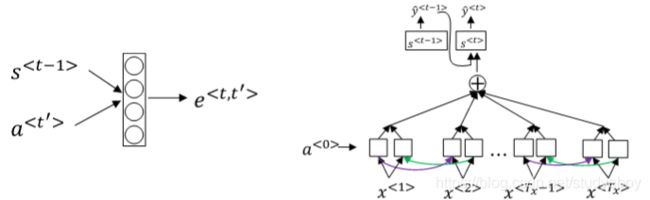
![]()
如上图所示,attention model仍由类似的编码网络(下)和解码网络(上)构成。其中, S < t > S^{
注意力模型(Attention Models)
Attention model能有效处理很多机器翻译问题,例如下面的时间格式归一化:
![]()
下图将注意力权重可视化:

上图中,颜色越白表示注意力权重越大,颜色越深表示权重越小。可见,输出语句单词与其输入语句单词对应位置的注意力权重较大,即对角线附近。
语音识别(Speech recognition)
深度学习中,语音识别的输入是声音,量化成时间序列。更一般地,可以把信号转化为频域信号,即声谱图(spectrogram),再进入RNN模型进行语音识别。

之前,语言学家们会将语音中每个单词分解成多个音素(phoneme),构建更精准的传统识别算法。但在end-to-end深度神经网络模型中,一般不需要这么做也能得到很好的识别效果。通常训练样本很大,需要上千上万个小时的语音素材。
语音识别的注意力模型(attention model)如下图所示:

一般来说,语音识别的输入时间序列都比较长,例如是10s语音信号,采样率为100Hz,则语音长度为1000。而翻译的语句通常很短,例如“the quick brown fox”,包含19个字符。这时候, T x T_x Tx与 T y T_y Ty差别很大。为了让 T x = T y Tx=Ty Tx=Ty,可以把输出相应字符重复并加入空白(blank),形如:
t t t _ h _ e e e _ _ _ ⊔ _ _ _ q q q _ _ ⋯ ttt \_ h\_eee\_ \_ \_ \sqcup\_ \_ \_ qqq\_ \_ \cdots ttt_h_eee___⊔___qqq__⋯
其中,下划线”_“表示空白,”⊔“表示两个单词之间的空字符。这种写法的一个基本准则是没有被空白符”_“分割的重复字符将被折叠到一起,即表示一个字符。
这样,加入了重复字符和空白符、空字符,可以让输出长度也达到1000,即 T x = T y T_x=T_y Tx=Ty。这种模型被称为CTC(Connectionist temporal classification)。
触发字检测(Trigger Word Detection)
触发字检测(Trigger Word Detection)在很多产品中都有应用,操作方法就是说出触发字通过语音来启动相应的设备。例如Amazon Echo的触发字是”Alexa“,百度DuerOS的触发字是”小度你好“,Apple Siri的触发字是”Hey Siri“,Google Home的触发字是”Okay Google“。

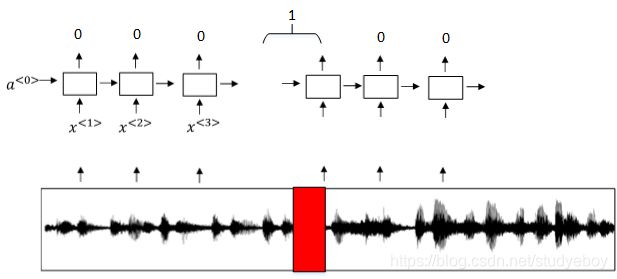
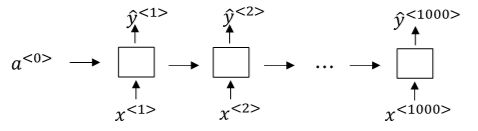
触发字检测系统可以使用RNN模型来建立。如下图所示,输入语音中包含一些触发字,其余都是非触发字。RNN检测到触发字后输出1,非触发字输出0。这样训练的RNN模型就能实现触发字检测。
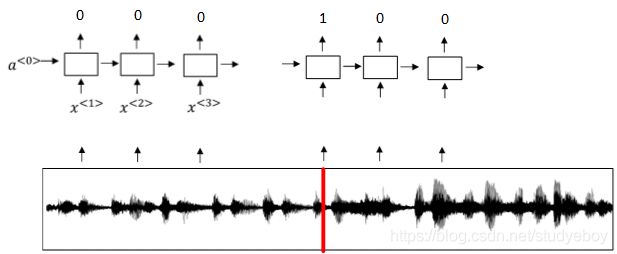
但是这种模型有一个缺点,就是通常训练样本语音中的触发字较非触发字数目少得多,即正负样本分布不均。一种解决办法是在出现一个触发字时,将其附近的RNN都输出1。这样就简单粗暴地增加了正样本。
参考资料
深度学习笔记(一)深度学习概论
吴恩达老师深度学习视频课笔记:总结
完结撒花!吴恩达DeepLearning.ai《深度学习》课程笔记目录总集
完结篇 | 吴恩达deeplearning.ai专项课程精炼笔记全部汇总
Coursera吴恩达《神经网络与深度学习》课程笔记(1)-- 深度学习概述
Coursera吴恩达《神经网络与深度学习》课程笔记(2)-- 神经网络基础之逻辑回归
Coursera吴恩达《神经网络与深度学习》课程笔记(3)-- 神经网络基础之Python与向量化
Coursera吴恩达《神经网络与深度学习》课程笔记(4)-- 浅层神经网络
Coursera吴恩达《神经网络与深度学习》课程笔记(5)-- 深层神经网络
Coursera吴恩达《优化深度神经网络》课程笔记(1)-- 深度学习的实用层面
Coursera吴恩达《优化深度神经网络》课程笔记(2)-- 优化算法
Coursera吴恩达《优化深度神经网络》课程笔记(3)-- 超参数调试、Batch正则化和编程框架
Coursera吴恩达《构建机器学习项目》课程笔记(1)-- 机器学习策略(上)
Coursera吴恩达《构建机器学习项目》课程笔记(2)-- 机器学习策略(下)
Coursera吴恩达《卷积神经网络》课程笔记(1)-- 卷积神经网络基础
Coursera吴恩达《卷积神经网络》课程笔记(2)-- 深度卷积模型:案例研究
Coursera吴恩达《卷积神经网络》课程笔记(3)-- 目标检测
Coursera吴恩达《卷积神经网络》课程笔记(4)-- 人脸识别与神经风格迁移
Coursera吴恩达《序列模型》课程笔记(1)-- 循环神经网络(RNN)
Coursera吴恩达《序列模型》课程笔记(2)-- NLP & Word Embeddings
Coursera吴恩达《序列模型》课程笔记(3)-- Sequence models & Attention mechanism
吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(2-1)-- 深度学习的实践方面
吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(2-2)-- 优化算法
吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(2-3)-- 超参数调试 和 Batch Norm
吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(3-1)-- 机器学习策略(1)
吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(3-2)-- 机器学习策略(2)
吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(4-1)-- 卷积神经网络基础
吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(4-2)-- 深度卷积模型
吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(4-3)-- 目标检测
吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(4-4)-- 特殊应用:人脸识别和神经风格迁移
吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(5-1)-- 循环神经网络
吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(5-2)-- NLP和词嵌入
吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(5-3)-- 序列模型和注意力机制