本文实例为大家分享了python基于numpy的线性回归的具体代码,供大家参考,具体内容如下
class类中包含:
创建数据
参数初始化
计算输出值,损失值,dw,db
预测函数
交叉验证函数
其中用到的数据集为sklearn中的糖尿病数据集
具体代码如下:
import numpy as np
from sklearn.utils import shuffle
from sklearn.datasets import load_diabetes
import matplotlib.pyplot as plt
#基于numpy实现一个简单的线性回归模型
#用class进行简单封装
class lr_model():
def __init__(self):
pass
# diabetes 是一个关于糖尿病的数据集, 该数据集包括442个病人的生理数据及一年以后的病情发展情况。
# 数据集中的特征值总共10项, 如下:
# 年龄
# 性别
# 体质指数
# 血压
# s1,s2,s3,s4,s4,s6 (六种血清的化验数据)
# 但请注意,以上的数据是经过特殊处理, 10个数据中的每个都做了均值中心化处理,然后又用标准差乘以个体数量调整了数值范围。验证就会发现任何一列的所有数值平方和为1.
def prepare_data(self):
data = load_diabetes().data
target = load_diabetes().target
#数据打乱
X, y = shuffle(data, target, random_state=42)
X = X.astype(np.float32)
y = y.reshape((-1, 1))#标签变成列向量形式
data = np.concatenate((X, y), axis=1)#横向变为数据标签的行向量
return data
#初始化参数,权值与偏执初始化
def initialize_params(self, dims):
w = np.zeros((dims, 1))
b = 0
return w, b
def linear_loss(self, X, y, w, b):
num_train = X.shape[0]#行数训练数目
num_feature = X.shape[1]#列数表示特征值数目
y_hat = np.dot(X, w) + b#y=w*x+b
loss = np.sum((y_hat - y) ** 2) / num_train#计算损失函数
dw = np.dot(X.T, (y_hat - y)) / num_train#计算梯度
db = np.sum((y_hat - y)) / num_train
return y_hat, loss, dw, db
def linear_train(self, X, y, learning_rate, epochs):
w, b = self.initialize_params(X.shape[1])#参数初始化
loss_list = []
for i in range(1, epochs):
y_hat, loss, dw, db = self.linear_loss(X, y, w, b)
w += -learning_rate * dw
b += -learning_rate * db#参数更新
loss_list.append(loss)
if i % 10000 == 0:#每到一定轮数进行打印输出
print('epoch %d loss %f' % (i, loss))
#参数保存
params = {
'w': w,
'b': b
}
grads = {
'dw': dw,
'db': db
}
return loss, params, grads,loss_list
#预测函数
def predict(self, X, params):
w = params['w']
b = params['b']
y_pred = np.dot(X, w) + b
return y_pred
#随机交叉验证函数,如何选测试集、训练集
def linear_cross_validation(self, data, k, randomize=True):
if randomize:
data = list(data)
shuffle(data)
slices = [data[i::k] for i in range(k)]#k为step
for i in range(k):
validation = slices[i]
train = [data for s in slices if s is not validation for data in s]#将不为测试集的数据作为训练集
train = np.array(train)
validation = np.array(validation)
yield train, validation#yield 变为可迭代,每次返回
if __name__ == '__main__':
lr = lr_model()
data = lr.prepare_data()
for train, validation in lr.linear_cross_validation(data, 5):
X_train = train[:, :10]
y_train = train[:, -1].reshape((-1, 1))
X_valid = validation[:, :10]
y_valid = validation[:, -1].reshape((-1, 1))
loss5 = []
loss, params, grads,loss_list = lr.linear_train(X_train, y_train, 0.001, 100000)
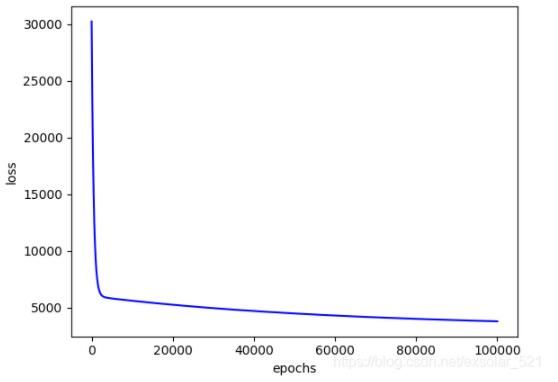
plt.plot(loss_list, color='blue')
plt.xlabel('epochs')
plt.ylabel('loss')
plt.show()
loss5.append(loss)
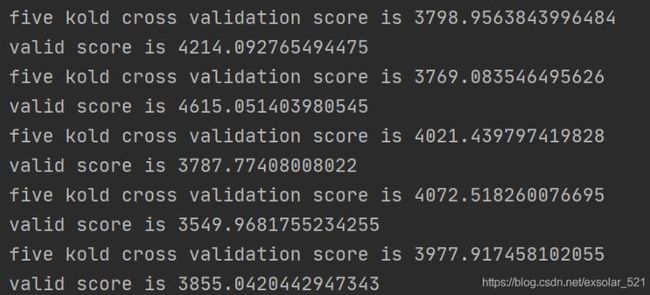
score = np.mean(loss5)
print('five kold cross validation score is', score)#5类数据的测试分数
y_pred = lr.predict(X_valid, params)
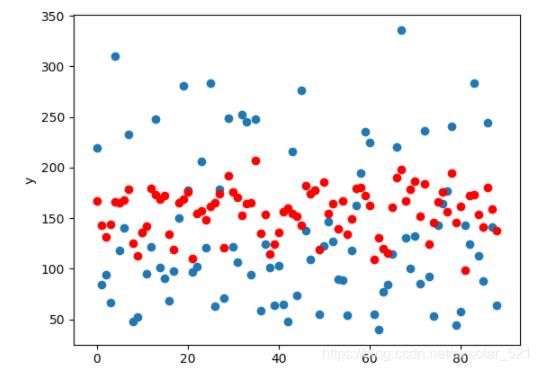
plt.scatter(range(X_valid.shape[0]),y_valid)
plt.scatter(range(X_valid.shape[0]),y_pred,color='red')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
valid_score = np.sum(((y_pred - y_valid) ** 2)) / len(X_valid)
print('valid score is', valid_score)
结果如下:
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持脚本之家。