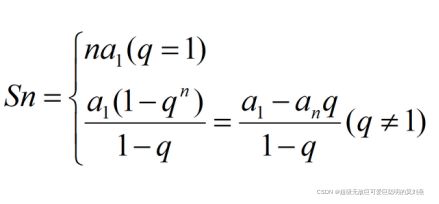【学习笔记】
学习笔记
- 一、枚举模拟
-
- 1.查找
-
- 1)杨辉三角形(查找):
- 2.排序
-
- 1)利用sort函数排序
- 2)快速排序
- 2)例题:双向排序
- 二、图论和数论
-
- 1.最短路
- 2.质因数分解
- 3.质数判断
-
- 1)厄拉多塞筛法求素数(查找范围内的所有质数)
- 4.最大公因数
- 5.最小公倍数
- 6.搜索
-
- DFS:所有组合等类似字眼时,我们第一感觉就要想到用dfs
- BFS:
- 二叉树
- 7.注意度、邻接阵的使用
- 三、动态规划
-
- 1.01背包型
- 2.线性递推型
- 3.区间动态型
- 4.状态压缩
- 四、算法模板
-
- 1.x的k进制拆分
- 2.并查集
- 五、小知识点
-
- 1.斐波那契数列与黄金分割:
- 2.修改数组:
- 3.公式和函数:
- 4.返回不正常值可能问题
- 5.位运算
- 6.vector
- 7.string
- 8.set
- 9.手算题
- 10.数据类型转换
一、枚举模拟
1.查找
1)杨辉三角形(查找):
杨辉三角每个值可看成C(a,b),中间对称,斜线递增,所以对斜线用*二分查找*
详解见:https://blog.csdn.net/weixin_44091134/article/details/116748883?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164920895016782246414942%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=164920895016782246414942&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-116748883.142^v5^pc_search_result_control_group,157^v4^control&utm_term=%E8%93%9D%E6%A1%A5%E6%9D%AF%E6%9D%A8%E8%BE%89%E4%B8%89%E8%A7%92&spm=1018.2226.3001.4187
#include2.排序
1)利用sort函数排序
排序sort(start,end,cmp)默认升序,cmp为排序规则
//改变Sort排序方式:
bool compareper(per& p1, per& p2)
{ if (p1.p_age == p2.p_age)
return p1.p_high > p2.p_high;
else
return p1.p_age < p2.p_age;
}
``
2)快速排序
(1)从数列中挑出一个元素,称为 "基准"(pivot);
(2)重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区操作;
(3)递归地把小于基准值元素的子数列和大于基准值元素的子数列排序;
Paritition1(int A[], int low, int high) {
int pivot = A[low];
while (low < high) {
while (low < high && A[high] >= pivot)
--high;
A[low] = A[high];
while (low < high && A[low] <= pivot)
++low;
A[high] = A[low];
A[low] = pivot;
return low; }
void QuickSort(int A[], int low, int high) //快排母函数
{
if (low < high) {
int pivot = Paritition1(A, low, high);
QuickSort(A, low, pivot - 1);
QuickSort(A, pivot + 1, high);
}
}
2)例题:双向排序
二、图论和数论
1.最短路
- Floyd算法,编写简单,复杂度高,可做填空
for (int k = 1; k <= maxn; k++) {
for (int i = 1; i <= maxn; i++) {
for (int j = 1; j <= maxn; j++) {
disFloyd[i][j] = disFloyd[j][i] = min(disFloyd[i][j], disFloyd[i][k] + disFloyd[k][j]);
}
}
}//k为点数,ij用来遍历数组 disfloyd为邻接矩阵
- Dijkstra算法,复杂度低,大题
void Dijkstra() {
memset(disDijk, 0x3f, sizeof(disDijk));
memset(vis, 0, sizeof(vis));
disDijk[1] = 0;
for (int i = 1; i <= 2021; i++) {
int curMin = 0x3f3f3f3f;
int curIndex = -1;
//找到当前未被置定的最小dij[j]点,置定
for (int j = 1; j <= 2021; j++) {
if (vis[j]) {
continue;
}
if (curMin > disDijk[j] || curIndex == -1) {
curMin = disDijk[j];
curIndex = j;
}
}
vis[curIndex] = true;
//更新加入j点后的dij ,dijk[j]=min(dijk[j],dijk[置定点]+置定点到j的距离,循环置定点相连的边的数量)
for (unsigned int j=curIndex+1; j<=curIndex+21&&j<=2021; j++) {
disDijk[j] = min(disDijk[j], disDijk[curIndex] + u[curIndex][j]);
}
}
}
2.质因数分解
例题:

问题可以转化成,将 2021041820210418分解成三个数 a∗b∗c 的形式,有多少种拆分方法。
将 2021041820210418质因数分解成可得:2021041820210418=2∗3^3∗17∗131∗2857∗5882353 。
对于质因数2,17,131,2857,5882353 2,17,131,2857,5882353 ,每个均可以分别分配给 a,b,c 三个位置,所以总共方法数是3^5。
对于出现了3次的质数3,可以枚举出其所有的分配方式,共10种。故总方法数为:3^5 * 10 = 2430。
/// 返回x的质因数分解结果,每一个pair的第一个元素为质因数p,第二个元素为指数a。
vector<pair<int, int> > GetPrimeFactor(int x) {
vector<pair<int, int> > ret;
for (int i = 2; i * i <= x; i++) {
if (x % i == 0) {
int cnt = 0;
while (x % i == 0) {
cnt++;
x /= i;
}
// x的质因子i出现了cnt次
ret.push_back(make_pair(i, cnt));
}
}
if (x > 1) {
ret.push_back(make_pair(x, 1));
}
return ret;
}
3.质数判断
1)厄拉多塞筛法求素数(查找范围内的所有质数)
public int CountPrimes(int n)
{
int count = 0;
bool[] signs = new bool[n];
for (int i = 2; i < n; i++)
{
//因为在 C# 中,布尔类型的默认值为 假。所以在此处用了逻辑非(!)操作符。
if (!signs[i])
{
count++;
for (int j = i + i; j < n; j += i)
{
//排除不是质数的数
signs[j] = true;
}
}
}
return count;
}
4.最大公因数
简短的写法:
int gcd(int x, int y) { return (x % y) ? gcd(y, x % y) : y; }
int lcm(int x, int y) { return x / gcd(x, y) * y; }
//辗转相除法
int divisor(int a, int b) {
int temp;
//比较两个数的大小,值大的数为a,值小的数为b
if (a < b) {
temp = a;
a = b;
b = temp;
}
//求余
while (b != 0) {
temp = a % b;
a = b;
b = temp;
}
return a;
}
5.最小公倍数
int minb(int i,int j)
{
int m,n;
int minb;
m=max(i,j);
n=min(i,j);
minb=m;
while(minb%n!=0)
{
minb+=m;
}
return minb;
}
6.搜索
DFS:所有组合等类似字眼时,我们第一感觉就要想到用dfs
本质上是暴力把所有的路径都搜索出来,它运用了回溯,保存这次的位置并深入搜索,都搜索完便回溯回来,搜下一个位置,直到把所有最深位置都搜一遍(找到目的解返回或者全部遍历完返回一个事先定好的值)。要注意的一点是,搜索的时候有记录走过的位置,标记完后可能要改回来
//算法模板;
int dfs(dep)//dep表深度
{
if(达到目的)处理return;
else
{
处理;
Dfs(dep+1);//下一深度
}
}
//例子:
void dfs(int i,string s[],int *a,int &count){
if(i>=11){
if(a[0]==1&&a[1]==4&&a[2]==3&&a[3]==3){
count++;
}
}else{
for(int j=0;j<s[i].size();j++){//此处可以结合剪枝,优化时间复杂度
if(s[i][j]=='1'){
a[j]+=1;
dfs(i+1,s,a,count);
a[j]-=1;//前面操作的步骤要进行反操作撤回
}
}
}
}
BFS:
它的思想是从一个被选定的点出发;然后从这个点的所有方向每次只走一步的走到底(即其中一个方向走完一步之后换下一个方向继续走);如果得不到目的解,那就返回事先定好的值,如果找到直接返回目的解。
1.设一个deque标记当前层可搜索的层,从队头取数据,取完以后删除
2.更新数据放进deque,直到deque为空 或者达到目的;

伪代码:(用num[i][j]表示第i行第j个位置走过没有)
因为初始起点需要走0步,我们把num数组 初始-1,mem(num,-1);
左上角为起点:
num[1][1]=0;
1 1进入队列
取出当前队列第一个元素(因为二维通常需要使用结构体)
判断它是否为终点位置?break:continue;
遍历该点四个方向可行方向
if(num[mx][my]==-1)
num[mx][my]=num[i][k]+1
把这个点进入队列。
结束
具体代码:
int bfs()
{
queue<node>q;
q.push({1,1});
num[1][1]=0;
while(!q.empty)
{
node u=q.front();q.pop();//扔掉首元素
for(int i=0;i<4;i++)
{
int mx=u.x+dx[i],my=u.y+dy[i];
if(u.x==ex&&u.y==ey) return num[u.x][u.y];//放队列之前我们已经把距离更新了,只要找到这个点绝对是最小距离了。
if(num[mx][my]==-1&&str[mx][my]==0)//这里还需要加一个判界,我就不手写了有点累了。
{
num[mx][my]=num[u.x][u.y]+1;
q.push({mx,my});
}
}
}
}
二叉树
二叉树遍历:前序遍历NLR、中序遍历LNR、后序遍历LRN
例题:98验证二叉搜索树
class Solution {
public:
long pre=LONG_MIN;
bool isValidBST(TreeNode* root) {
if(root==nullptr)
return true;
if(!isValidBST(root->left))
return false;
if(root->val<=pre)
return false;
pre=root->val;
return isValidBST(root->right);
}
};
7.注意度、邻接阵的使用
三、动态规划
1.01背包型
介绍见CSDN博主「HarryXxc」的原创文章原文链接:https://blog.csdn.net/harryshumxu/article/details/106427093
#include 2.线性递推型
介绍见CSDN博主「小杨_小杨」的原创文章,原文链接:https://blog.csdn.net/weixin_45843077/article/details/104194693
3.区间动态型
介绍见:CSDN博主「纯木」的原创文章,原文链接:https://blog.csdn.net/u012679087/article/details/84109739
注意:破环为链
关于环和直线区间动态区别见:
https://blog.csdn.net/qq_37006625/article/details/84760039
4.状态压缩
集合问题例如:(1)子集问题,设元素无先后关系,那么共有 2 n 2^n 2n个子集;(2)排列问题,对所有元素进行全排列,共有 n ! n! n!个全排列。
状态压缩DP的思想:集合的状态(子集或排列)用二进制表示状态,并用二进制的位运算来遍历和操作
介绍见CSDN博主「罗勇军」的原创文章,原文链接:https://blog.csdn.net/weixin_43914593/article/details/106432695
四、算法模板
1.x的k进制拆分
// 返回x的k进制表示
vector<int> Split(int x, int k) {
vector<int> ret;
if (x == 0) { // 如果输入数据就是0那么需要返回一个单独的0数字
ret.push_back(0);
return ret;
}
while (x > 0) {
ret.push_back(x % k);
x /= k;
}
reverse(ret.begin(), ret.end());
return ret;
}
2.并查集
分为并和查两部分,定义一个数组存放父节点;一般可用于分块/类
集合树:所有节点以代表节点为父节点构成的多叉树
节点的代表节点:可以理解为节点的父节点,从当前节点出发,可以向上找到的第一个节点
集合的代表节点:可以理解为根节点,意味着该集合内所有节点向上走,最终都能到达的节点
int find(int x)
{
if(x==parent[x]) return x;
returnparent[x]=find(parent[x]);
}
void Union(int a,int b)
{
intpa=find(a);
intpb=find(b);
if(pa!=pb) parent[pa]=pb;
}
五、小知识点
1.斐波那契数列与黄金分割:
因为趋近,所以当输入达到一定范围后,输出一致,所以可以直接输出结果
2.修改数组:
并查集,用数组来表示关系,可以不用存储之间输出
3.公式和函数:
-
1b=8位二进制
-
等差数列前n项和为n(a1+an)/2
-
如何确定直线:两点确定一条
点是否在直线上:三点距离为a+b=c时,
两条线是否重合:两点是否都在另一线上 -
最小公倍数=x*y/最大公因数。
-
互质:公约数只有1的两个自然数(最大公约数为1)
-
可以判特例骗分
-
浮点数判定是否相等不是直接相等,而是差值小于某数,eg.le-5
-
reverse函数用于反转在[first,last)范围内的顺序(包括first指向的元素,不包括last指向的元素),常用于数组,字符串,容器等。#include
-
pow(i,3)//求i的三次方
-
求根号用double sqrt(double x)
-
浮点数绝对值fabs(),整数绝对值用abs()
-
memset(u, 0x3f, sizeof(u));//u可以是二维数组,将u全赋0x3f(int类型的极值,float为0x4f
-
用 j * j <= i 代替 j <= √i 会更好
-
for(auto c:s)//对于s中的每个字符
for(auto &c:s);//对于s中的每个字符,c是一个引用,赋值语句将会改变s中字符的值
4.返回不正常值可能问题
3221225477 (0xC0000005): 访问越界,一般是读或写了野指针指向的内存
3221225725 (0xC00000FD): 堆栈溢出,一般是无穷递归造成的
3221225620 (0xC0000094): 除0错误,一般发生在整型数据除了0的时候
5.位运算
1)按位与&:清零(与一个各位都为零的数值相与) 取一个数中指定位(该数的对应位为1,其余位为零)
2)按位或|:将某位置一
3)异或^:对应位翻转(异或对应1)
4)取反~
5)左移<<:左移一位=*2
6)右移>>:右移一位=/2
6.vector
二维数组初始化存放数据:先建一个一维vector,在push进二维
Vector初始化时可以先用resize预设内存,即可下标访问
Vector要初始化以后才能用下标访问
7.string
string 类提供了 6 种查找函数,每种函数以不同形式的 find 命名。
这些操作全都返回 string::size_type 类型的值,以下标形式标记查找匹配所发生的位置;
或者返回一个名为 string::npos 的特殊值,说明查找没有匹配。string 类将 npos 定义为保证大于任何有效下标的值。
当 str.find(“哦”)==string::npos时则说明字符串str中不存在“哦”,
反之,str.find(“哦”)!=string::npos则说明字符串str中存在“哦”
8.set
可以利用set不重复的功能来确定不同的数量,set可以不用判断浮点型精度问题
9.手算题
介绍见:https://blog.csdn.net/weixin_43914593/article/details/115795620
10.数据类型转换
int转string
stringstream sstream;
string strResult;
int nValue = 1000;
// 将int类型的值放入输入流中
sstream << nValue;
// 从sstream中抽取前面插入的int类型的值,赋给string类型
sstream >> strResult;
string转int
stringstream sstream;
int first, second;
// 插入字符串
sstream << "456";
// 转换为int类型
sstream >> first;
bool转int
// 在进行多次类型转换前,必须先运行clear()
sstream.clear();
// 插入bool值
sstream << true;
// 转换为int类型
sstream >> second;
多个字符串拼接和stringstream类的清空
stringstream sstream;
// 将多个字符串放入 sstream 中
sstream << "first" << " " << "string,";
sstream << " second string";
cout << "strResult is: " << sstream.str() << endl;
// 清空 sstream
sstream.str("");