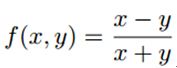人脸检测之NPD（Normalized Pixel Difference）

个人拙见：

 

归一化的像素差异特征Normalized PixelDifference (NPD)，出自TPAMI上A Fast and AccurateUnconstrained Face Detector 这篇文章。是李子青组2015年的一篇论文。并且该方法的检测和训练的程序，作者已经开源，非常的值得借鉴。是传统的机器学习方面一篇很有影响的人脸检测的论文。

NPD方法的优势：

（1）可以基于cpu的多线程OpenMP，pthread做并行化处理，当然也可以基于GPU的CUDA做并行处理。本来原始程序的运行速度就很不错，在并行化处理后可以达到非常快的实时速度。

（2）该方法是一种unsonstrained的人脸检测方法，非常适合现实生活的检测环境。

（3）NPD特征通过查找表（look up table）获得，避免了每次的重新运算，加速了程序预处理速度。

不足之处：

（1）训练的程序是将所有图像都存储到一个Mat格式的文件中，这样就导致非常不利于大型模型的训练，当存储的图片数量很大时，这样的方式就是个瓶颈。本人修改这块的程序，将图片分批量的读取进行训练，可以使内存占有率大大降低。

       下图中，左面为原始的程序的训练占用内存情况，右图为本人改进后的内存占用情况。

（2）由于论文作者训练的模型的窗口大小是20*20，作者提出的NPD特征会伴随着训练的窗口的大小变化做相应的2次方增长，简单的说就是说NPD特征的维数是不恒定的，具体和训练的窗口大小相关。

       假设一个窗口中有P个点，那么其中任意两个点都会产生一个特征值，就是

       C(P，2)=P*(P-1)/2

       那么20*20的窗口将产生20*20*（20*20-1）/2=79800维度的特征向量。

如果自己实际需要的场景的人脸比较大，比如，用一个20*20训练的模型去检测180*180的人脸就不是一个很好的选择，因为中间涉及到了滑动步长和时间的折中。一个合理的解释是自己训练的模型和实际需要检测的环境的大小越接近，检测效果越好，速度越快。但是如果这个时候训练一个180*180的窗口模型，得到的特征向量将会是多大啊。本人的改进就是加上PCA降维，维度保持恒定，不受模型大小的影响，个中细节不再赘述。

      

NPD特征的解释：

         NPD特征就是检测2个像素之间的差异性（有点类似Viola Johns），该差异定义为函数f(x,y)。其中，x，y为任意两个像素的像素值。并且规定f(0,0)=0。

该函数的曲线如下所示：

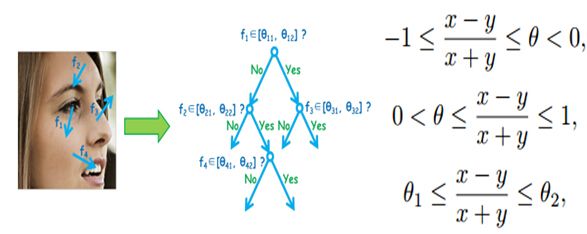
深度二叉树：

如上式所示，其中x为NPD特征，a,b,c为常量，t为阈值。

如上图所示，对于第一个公式，表明像素x比像素y颜色要明显的深，就好比左图的f1，对于第二个公式，表明，像素x比像素y的颜色要明显的亮，就像左图f2所示，对于第三个公式，表明像素x和像素y的明暗不确定，好比左图的f3，f4，对于f3，x的像素基本就是肤色，而这个是不确定的，同样的y的颜色是背景，而这个也是不确定的。

       对于该深度二叉树，可以通过训练，自己学习到上面说的3中情形，然后通过一个一个的深度二叉树实现对于人脸的分类。

       简单的说，2个点，一个是特征向量：NPD，一个是分类器：深度二叉树。这就是传统模式识别的2个改进方向，作者既提出了自己的特征向量，又提出了一个基于二叉树的分类器。当然了NPD特征和Viola Johns有点相似，深度二叉树又和cascade级联分类器有点类似。

 

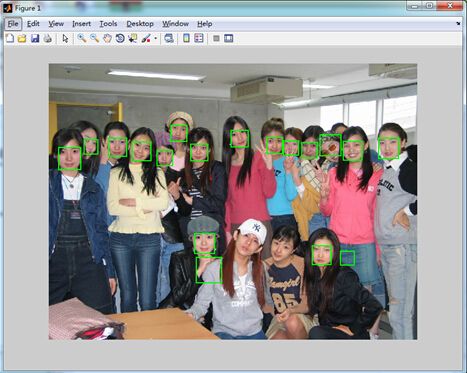
程序运行效果：

程序的官方下载链接：http://www.cbsr.ia.ac.cn/users/scliao/projects/npdface/，程序的官方版本是Matlab版本，当然中间也利用了c++的多线程进行了混合编程，但是程序主题还是M语言的。当然github上也有热心网友的c++版本，效果还是很不错的。

plus：

使用matlab将matlab训练生成的npdModel.mat转化为npdModel.txt，供c++程序使用，without matio

load('npdModel.mat');
fid=fopen('npdModel.txt','wt');
% objSize
fprintf(fid,'%g\t',npdModel.objSize);
% numStages
fprintf(fid,'%g\t',npdModel.numStages);
% numBranchNodes
fprintf(fid,'%g\t',npdModel.numBranchNodes);
% numLeafNodes
fprintf(fid,'%g\t',npdModel.numLeafNodes);
% scaleFactor
fprintf(fid,'%g\t',npdModel.scaleFactor);
% numScales
fprintf(fid,'%g\n',npdModel.numScales);
% stageThreshold
fprintf(fid,'%g\t',length(npdModel.stageThreshold(:,1)));
fprintf(fid,'%g\n',length(npdModel.stageThreshold(1,:)));

for i=1:length(npdModel.stageThreshold(:,1))
    fprintf(fid,'%g\n',npdModel.stageThreshold(i,1));
end
% treeRoot
fprintf(fid,'%g\t',length(npdModel.treeRoot(:,1)));
fprintf(fid,'%g\n',length(npdModel.treeRoot(1,:)));

for i=1:length(npdModel.treeRoot(:,1))
    fprintf(fid,'%g\n',npdModel.treeRoot(i,1));
end
% pixel1
fprintf(fid,'%g\t',length(npdModel.pixel1(:,1)));
fprintf(fid,'%g\n',length(npdModel.pixel1(1,:)));

for i=1:length(npdModel.pixel1(:,1))
    for j=1:length(npdModel.pixel1(1,:))
        if j==length(npdModel.pixel1(1,:))
           fprintf(fid,'%g\n',npdModel.pixel1(i,j)); 
        else
            fprintf(fid,'%g\t',npdModel.pixel1(i,j));
        end
        
    end
end

% pixel2
fprintf(fid,'%g\t',length(npdModel.pixel2(:,1)));
fprintf(fid,'%g\n',length(npdModel.pixel2(1,:)));

for i=1:length(npdModel.pixel2(:,1))
    for j=1:length(npdModel.pixel2(1,:))
        if j==length(npdModel.pixel2(1,:))
           fprintf(fid,'%g\n',npdModel.pixel2(i,j)); 
        else
            fprintf(fid,'%g\t',npdModel.pixel2(i,j));
        end
        
    end
end
% cutpoint
fprintf(fid,'%g\t',length(npdModel.cutpoint(:,1)));
fprintf(fid,'%g\n',length(npdModel.cutpoint(1,:)));

for i=1:length(npdModel.cutpoint(:,1))
    for j=1:length(npdModel.cutpoint(1,:))
        if j==length(npdModel.cutpoint(1,:))
           fprintf(fid,'%g\n',npdModel.cutpoint(i,j)); 
        else
            fprintf(fid,'%g\t',npdModel.cutpoint(i,j));
        end
        
    end
end
% leftChild
fprintf(fid,'%g\t',length(npdModel.leftChild(:,1)));
fprintf(fid,'%g\n',length(npdModel.leftChild(1,:)));

for i=1:length(npdModel.leftChild(:,1))
    for j=1:length(npdModel.leftChild(1,:))
        if j==length(npdModel.leftChild(1,:))
           fprintf(fid,'%g\n',npdModel.leftChild(i,j)); 
        else
            fprintf(fid,'%g\t',npdModel.leftChild(i,j));
        end
        
    end
end
% rightChild
fprintf(fid,'%g\t',length(npdModel.rightChild(:,1)));
fprintf(fid,'%g\n',length(npdModel.rightChild(1,:)));

for i=1:length(npdModel.rightChild(:,1))
    for j=1:length(npdModel.rightChild(1,:))
        if j==length(npdModel.rightChild(1,:))
           fprintf(fid,'%g\n',npdModel.rightChild(i,j)); 
        else
            fprintf(fid,'%g\t',npdModel.rightChild(i,j));
        end
        
    end
end
% fit
fprintf(fid,'%g\t',length(npdModel.fit(:,1)));
fprintf(fid,'%g\n',length(npdModel.fit(1,:)));

for i=1:length(npdModel.fit(:,1))
    for j=1:length(npdModel.fit(1,:))
        if j==length(npdModel.fit(1,:))
           fprintf(fid,'%g\n',npdModel.fit(i,j)); 
        else
            fprintf(fid,'%g\t',npdModel.fit(i,j));
        end
        
    end
end
% npdTable
fprintf(fid,'%g\t',length(npdModel.npdTable(:,1)));
fprintf(fid,'%g\n',length(npdModel.npdTable(1,:)));

for i=1:length(npdModel.npdTable(:,1))
    for j=1:length(npdModel.npdTable(1,:))
        if j==length(npdModel.npdTable(1,:))
           fprintf(fid,'%g\n',npdModel.npdTable(i,j)); 
        else
            fprintf(fid,'%g\t',npdModel.npdTable(i,j));
        end
        
    end
end

% winSize
fprintf(fid,'%g\t',length(npdModel.winSize(:,1)));
fprintf(fid,'%g\n',length(npdModel.winSize(1,:)));

for i=1:length(npdModel.winSize(:,1))
    for j=1:length(npdModel.winSize(1,:))
        if j==length(npdModel.winSize(1,:))
           fprintf(fid,'%g\n',npdModel.winSize(i,j)); 
        else
            fprintf(fid,'%g\t',npdModel.winSize(i,j));
        end
        
    end
end
fclose(fid);