数据结构课程笔记总结1 - 排序算法
排序算法
1. 时间复杂度为2^N的排序算法
(1) 选择排序
从列表里,每次都选择一个最小或者最大的,然后去掉该值后,在剩下的数字里,继续选择最大或者最小的,依次下去,最后整个数组排好序。
一次保证有一个数字到位
public static void selectionSort(int[] arr){
if(arr!=null || arr.length>=2){
for(int i=0;i<arr.length-1;i++){
int minIndex = i;
for(int j = i+1;j< arr.length;j++){
minIndex = arr[j]<arr[minIndex]?j:minIndex;
}
swap(arr,i,minIndex);
}
}
}
public static void swap(int[] arr, int index, int minIndex){
if(arr[minIndex]<arr[index]){
int tmp;
tmp = arr[index];
arr[index]=arr[minIndex];
arr[minIndex]=tmp;
}
}
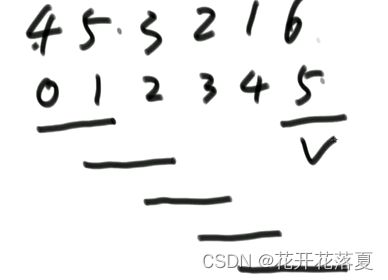
(2) 冒泡排序
当需要数组递增时,一遍遍从index=0遍历,将相对大的数字换到后面。
public static void bubbleSort(int[] arr){
if(arr!=null || arr.length>=2){
for(int i = arr.length-1;i>0;i--){
//0~N-1
//0~N-2
for(int j=0;j<i;j++){
if(arr[j]>arr[j+1]){
swap(arr,j,j+1);
}
}
}
}
}
public static void swap(int[] arr, int src, int dis){
int tmp;
tmp = arr[src];
arr[src]=arr[dis];
arr[dis]=tmp;
}
(3) 插入排序
从左开始,逐渐划定范围,先让小区间有序,再一步步扩大范围。
一次保证一个数字相对有序
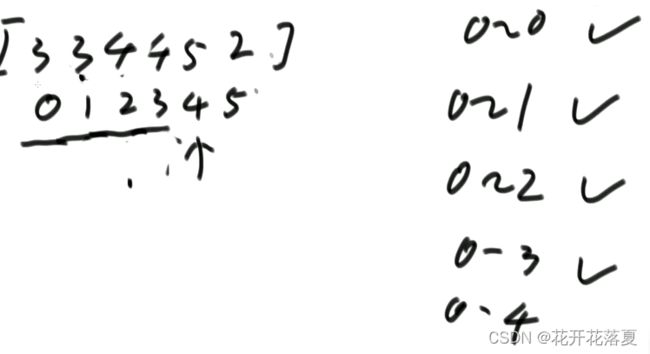
代码:
public static void insertSort(int[] arr){
if(arr!=null || arr.length>=2){
for(int i=0;i< arr.length;i++){
for(int j = i;j>0;j--){
if(arr[j]<arr[j-1]){
swap(arr,j,j-1);
}else{
break;
}
}
}
}
}
public static void swap(int[] arr, int src, int dis){
int tmp;
tmp = arr[src];
arr[src]=arr[dis];
arr[dis]=tmp;
}
2. 时间复杂度为N*log(N)的排序算法
(1) 归并排序
递归方法
整体是递归的,左边排好序,右边排好序,merge让整体有序。让其整体有序的过程中用了排外序方法。利用master公式来求解时间复杂度。
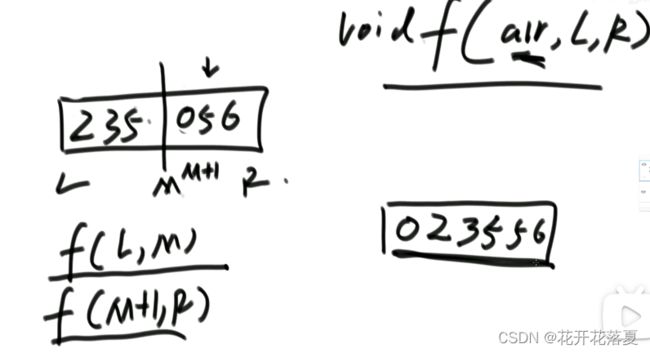
private static void mergeSort(int[] arr) {
if (arr != null && arr.length > 1) {
process(arr, 0, arr.length - 1);
}
}
private static void process(int[] arr, int left, int right) {
if (left == right) {
return;
} else {
int mid = left + ((right - left) >> 1);
process(arr, left, mid);
process(arr, mid + 1, right);
merge(arr, left, mid, right);
}
}
private static void merge(int[] arr, int left, int mid, int right) {
int[] tmp = new int[right - left + 1];
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
tmp[k++] = arr[i++];
} else {
tmp[k++] = arr[j++];
}
}
if (i <= mid) {
while (i <= mid) {
tmp[k++] = arr[i++];
}
}
if (j <= right) {
while (j <= right) {
tmp[k++] = arr[j++];
}
}
k = 0;
for (i = left; i <= right; i++) {
arr[i] = tmp[k++];
}
}
非递归
使用步长切分数组,将每一个步长内的数组排好序。再加大步长,直到步长和数组长度相等。
其中mergeSize为1,2,4,8…翻倍增长。
非递归的思路,就是通过mergeSize来切分数组为小数组,再将两两的小数组合并排序。
private static void mergeSort(int[] arr) {
if (arr != null && arr.length > 1) {
int mergeSize = 1;
while (mergeSize < arr.length) {
int left = 0;
while (left < arr.length) {
int m = left + mergeSize - 1;
int right = Math.min(m + mergeSize, arr.length - 1);
merge(arr, left, m, right);
left = right + 1;
}
if (mergeSize > arr.length / 2) {//防止int类型溢出
break;
}
mergeSize <<= 1;
}
}
}
private static void merge(int[] arr, int left, int mid, int right) {
int[] tmp = new int[right - left + 1];
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
tmp[k++] = arr[i++];
} else {
tmp[k++] = arr[j++];
}
}
if (i <= mid) {
while (i <= mid) {
tmp[k++] = arr[i++];
}
}
if (j <= right) {
while (j <= right) {
tmp[k++] = arr[j++];
}
}
k = 0;
for (i = left; i <= right; i++) {
arr[i] = tmp[k++];
}
}
拓展1
求数组小和
在一个数组中,一个数左边比它小的数的总和,叫做数的小和,所有数的小和累加起来,叫数组小和。求数组小和。

可以使用merge排序的思想来考虑这个问题。每次merge时,左边数组内部有序,右边数组内部有序。当左边数组的当前值小于右边数组的当前值时,左边数组的当前数是小和的组成之一,且右边数组当前值及其后面的值有多少个数,此值就组成了多少次小和。当数组只有一个数时,此时不存在小和。
private static int minSummary(int[] arr,int left,int right){
if(left==right){
return 0;
}else{
int mid = left + ((right-left)>>1);
return minSummary(arr,left,mid) + minSummary(arr,mid+1,right)+ merge(arr,left,mid,right);
}
}
private static int merge(int[] arr, int left, int mid, int right) {
int result = 0;
int[] tmp = new int[right - left + 1];
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) {
if (arr[i] < arr[j]) {
result += arr[i]*(right-j+1);
tmp[k++] = arr[i++];
} else {
tmp[k++] = arr[j++];
}
}
if (i <= mid) {
while (i <= mid) {
tmp[k++] = arr[i++];
}
}
if (j <= right) {
while (j <= right) {
tmp[k++] = arr[j++];
}
}
k = 0;
for (i = left; i <= right; i++) {
arr[i] = tmp[k++];
}
return result;
}
拓展2
求数组的降序对
若一个数,比它后面的数大,则为降序对。
可以使用merge排序的倒序排法,每次merge时,左边数组内部有序,右边数组内部有序,皆为倒序。当左边数组的当前值大于右边数组的当前值时,说明有降序对,且右边数组当前值及其后面的值有多少个数,此值有多少个降序对。当数组只有一个数时,此时不存在降序对。
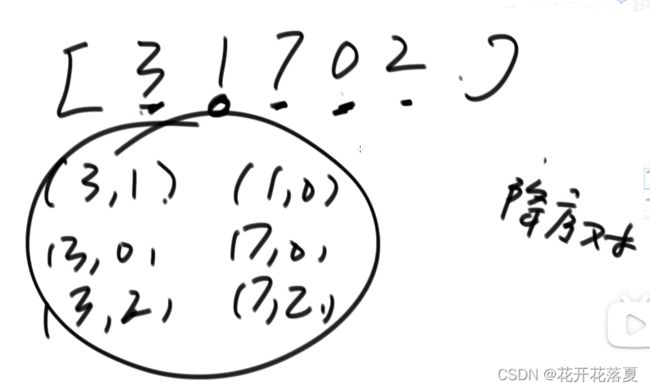
private static int findDescendingPairs(int[] arr,int left,int right){
if(left==right){
return 0;
}else{
int mid = left + ((right-left)>>1);
return findDescendingPairs(arr,left,mid) + findDescendingPairs(arr,mid+1,right)+ merge(arr,left,mid,right);
}
}
private static int merge(int[] arr, int left, int mid, int right) {
int result = 0;
int[] tmp = new int[right - left + 1];
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) {
if (arr[i] > arr[j]) {
result += right-j+1;
tmp[k++] = arr[i++];
} else {
tmp[k++] = arr[j++];
}
}
if (i <= mid) {
while (i <= mid) {
tmp[k++] = arr[i++];
}
}
if (j <= right) {
while (j <= right) {
tmp[k++] = arr[j++];
}
}
k = 0;
for (i = left; i <= right; i++) {
arr[i] = tmp[k++];
}
return result;
}
(2) 快速排序
导言
Partition过程
给定一个数组arr,和一个整数num,请把小于等于num的数放在数组的左边,大于等于num的数放在数组的右边。
要求额外空间复杂度为O(1),时间复杂度为O(N)
思路:可以使用双指针来解决这个问题,指针left指向数组左边,指针right指向数组右边。若left所指向的值小于等于num, 则left++,若right指向的值大于num,则right–。当left指向的值大于num, left指针不动,等待一个right指针的值小于等于num, 此时交换双方的值。对于right指针同理。直到left==right,则程序退出。
private static void partitionArr(int[] arr, int tmp){
if(arr!=null && arr.length>1){
int left = 0, right = arr.length-1, swap;
while (left<right){
if(arr[left]> tmp && arr[right]<=tmp){
swap = arr[left];
arr[left] = arr[right];
arr[right] = swap;
left++;
right--;
}
if(arr[left]<=tmp){
left ++;
}
if(arr[right]>tmp){
right--;
}
}
}
}
另一种解法,划区域
有一个区域标志,border,初始值设为-1,遍历数组。当arr[i]的值,小于等于num,则将此值与border+1位置的值交换,border++,i++。当arr[i]的值大于num时,i++, border不动。最后遍历完整个数组之后程序退出。border边界里都是小于等于num的数。

private static void partitionArr(int[] arr, int tmp) {
if (arr != null && arr.length > 1) {
int border = -1, swap;
for (int i = 0; i < arr.length; i++) {
if (arr[i] <= tmp) {
swap = arr[border + 1];
arr[border + 1] = arr[i];
arr[i] = swap;
border++;
}
}
}
}
快速排序
基本思想:先从数组中取出一个数作为基准数,分区过程中将大于这个数的都放在右边,小于等于这个数的全都放在左边,再对左右区间重复着一过程,直到各区间都只有一个数。
private static void quickSort(int[] arr,int left, int right){
if(left>=right){
return;
}else{
//此操作为随机选择一个数作为划分target值
//若不进行此操作,当数组有序时,再进行快速排序,时间复杂度就有可能
为O(N^2)
//每次随机选择一个数,减少了每次递归,左右两边的数组体量差距特别大的情况
swap(arr,left+(int)(Math.random()*(right-left+1)),right);
int[] indexList = partitionArr(arr,left,right);
quickSort(arr,left,indexList[0]-1);
quickSort(arr,indexList[1]+1,right);
}
}
private static int[] partitionArr(int[] arr, int left, int right) {
int leftIndex = left - 1, rightIndex = right, target = arr[right],i=left;
while (i<rightIndex){
if(arr[i]==target){
i++;
}else if (arr[i] < target) {
swap(arr, leftIndex+1, i);
leftIndex++;
i++;
} else if (arr[i] > target) {//We must to check the new value of arr[i]
swap(arr, i, rightIndex - 1);
rightIndex--;
}
}
swap(arr, rightIndex, right);
return new int[]{leftIndex + 1, rightIndex};
}
private static void swap(int[] arr, int source, int target) {
int swap = arr[source];
arr[source] = arr[target];
arr[target] = swap;
}
总结:通过分析可知,快速排序的划分值越靠近中间,性能越好;越靠近两边,性能越差。随机选一个数进行划分的目的就是让好情况和差情况都变成概率事件。最终结果就是,时间复杂度O(N*logN),额外空间复杂度O(logN)都是这么来的。
(3) 堆排序
堆结构就是用数组实现的完全二叉树结构。完全二叉树中如果每棵子树的最大值都在顶部就是大根堆。完全二叉树中如果每棵子树的最小值都在顶部就是小根堆。
对于数组实现,左孩子位置:2i+1,右孩子位置:2i+2,父节点:(i-1)/2
大根堆:
每插入一个数,将此数与父节点的数作比较,若大于父节点的数,则与父节点的数做交换。一直到父节点为根节点,或者此数小于父节点为止。
小根堆:
孩子数值大于父节点数值
堆排序思路如代码,空间复杂度为O(1)
public void heapSort(int[] arr){
for(int i =0;i<arr.length;i++){
heapInsert(arr,i);
}
int heapSize = arr.length;
swap(arr,0,--heapSize);
while (heapSize>0){
heapify(arr,--heapSize);
swap(arr,0,heapSize);
}
for(int i:arr){
System.out.println(i);
}
}
//当我们插入一个值,我们需要比较此值与父节点的值。若父节点的值大于此值,则直接将值放置在数组中
//若父节点的值小于此值,则交换父节点与此节点位置。再比较父节点与祖父节点,一直比较并交换到父节点大于子节点,或者根节点为止
public void heapInsert(int[] arr, int i) {
while (arr[(i - 1) / 2] < arr[i]) {
swap(arr, i, (i - 1) / 2);
i = (i - 1) / 2;
}
}
//将根位置与子节点最大的值交换。一直交换下去,直到父节点大于子节点所有数,或者没孩子。
public void heapify(int[] arr, int heapSize) {
int leftIndex = 1, maxIndex, index = 0;
while (leftIndex <= heapSize) {//有左孩子
maxIndex = leftIndex + 1 <= heapSize && arr[leftIndex + 1] > arr[leftIndex] ? leftIndex + 1 : leftIndex;
if (arr[index] >= arr[maxIndex]) {
break;
} else {
swap(arr, index, maxIndex);
}
index = maxIndex;
leftIndex = index * 2 + 1;
}
}
public void swap(int[] arr, int index1, int index2){
int tmp = arr[index1];
arr[index1] = arr[index2];
arr[index2] = tmp;
}
注意:
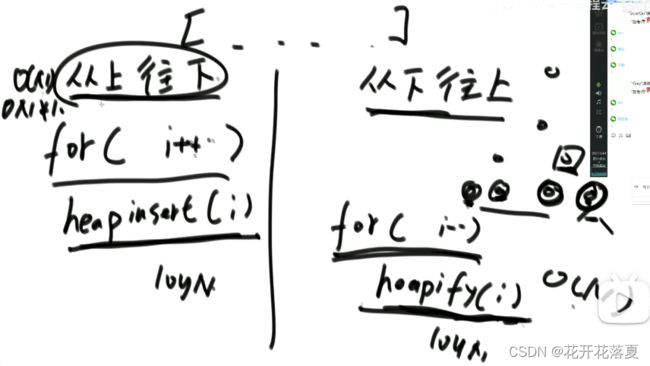
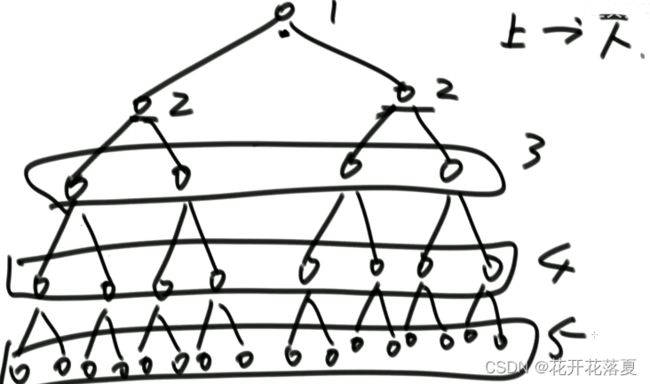
① 将数据一个个插入的heapInsert行为,时间复杂度为N*logN,若一次性给了所有数据,可以使用heapify的思路将数组调成堆,从最后一个数字开始看起,若不是大根堆就换成大根堆,可以优化时间复杂度为logN。
② Java里的PriorityQueue默认使用的小根堆。
可以给PriorityQueue里传入一个倒序的比较器,把PriorityQueue变为大根堆。
public static class MyComparator implements Comparator<Integer>{
public int compare(Integer o1, Integer o2){
return o2-o1;
}
}
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(new MyComparator());
例题: 已知一个几乎有序的数组。几乎有序是指,如果把数组排好顺序的话,每个元素移动的距离一定不超过k,并且k相对于数据长度来说是比较小的。
请选择一个合适的排序策略,对这个数组进行排序。
几乎有序,代表着若是从小到大排序,则在k位置内,我一定能找到符合K位置时间段里的最小值。
此时使用堆排序很合适,因此堆的层数,可以不超过log2
public static void minHeap(int[] arr, int k) {
int limit = Math.min(arr.length - 1, k), i = 0, j = 0;
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
for (; i <= limit; i++) {
minHeap.add(arr[i]);
}
while (i < arr.length) {
minHeap.add(arr[i]);
arr[j++] = minHeap.poll();
i++;
}
while (!minHeap.isEmpty()) {
arr[j++] = minHeap.poll();
}
}
3. 不基于比较的排序
(1)桶排序
桶排序思想下的排序:计数排序 & 基数排序
(1)桶排序思想下的排序都是不基于比较的排序
(2)时间复杂度为O(N),额外空间复杂度为O(M)
(3) 应用范围有限,需要样本的数据情况满足桶的划分
例子:有一个数组,按照最后一位数的大小,对数组进行排序
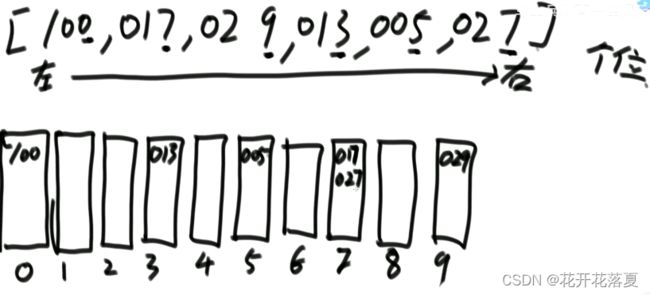
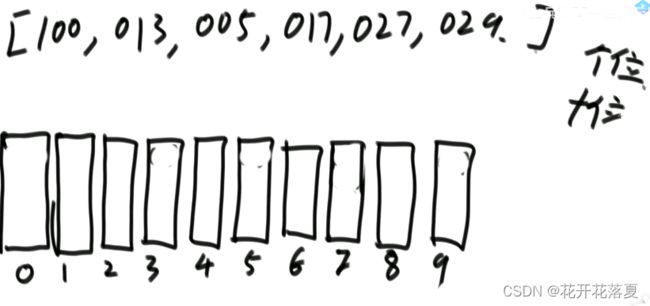
这样实现内存消耗过大,优化过程如下:
个位数的范围为0~9, 首先创建一个数组,为count,里面遍历了数组中的数,统计数组中有多少个数以0~9结尾。
再创建一个count’数组,若对数组排好序,则个位数为0的在最前面,为1的紧跟着,为2的再次,最后为以9为个位数的数子。因此count数组中的值,代表以Index为个位数的数字,最大的范围,例如index=1时,由于个位数为0的数有一位,放置位置为1,个位数为1的数有两位,所以放置个位数为1的位置为2~3,即count’[1]=3.依次下去。
help数组,为真正排好序的数组,在构成help数组时,由于我们只知道对应个位数放置的最大位置,就从后往前倒排数组。
对于403,个位数为3,对应的最大位置是6,由于help数组从0开始,因此将403放入count’[3]-1的位置,即help[5]=403.

代码:
private static int[] baseNumberSort(int[] numberList) {
int lastNumber;
int[] count = new int[10];
int[] indexList = new int[10];
int[] help = new int[numberList.length];
for (int number : numberList) {
count[getLastNumber(number)]++;
}
int sum = 0;
for (int i = 0; i < count.length; i++) {
sum += count[i];
indexList[i] = sum;
}
for (int j = numberList.length - 1; j >= 0; j--) {
lastNumber = getLastNumber(numberList[j]);
help[indexList[lastNumber] - 1] = numberList[j];
indexList[lastNumber]--;
}
return help;
}
private static int getLastNumber(int number) {
String str = String.valueOf(number);
return Integer.parseInt(str.substring(str.length() - 1));
}
计数排序和基数排序
一般来讲,计数排序要求,样本是整数,且范围比较窄。基数排序要求,样本是10进制的正整数。一对于计数或基数排序,一旦要求稍有升级,改写代价增加是显而易见的。
4. 其他排序
(1)比较器(comparator)
对于比较器,返回负数,第一个参数在前面;返回正数,第二个参数在前面;返回0,谁在前面无所谓。
升序:第一个数减第二个数
降序:第二个数减第一个数
List<Student> studentList = new ArrayList<>();
studentList.add(new Student(3, "C"));
studentList.add(new Student(1, "A"));
studentList.add(new Student(2, "B"));
Collections.sort(studentList, Comparator.comparingInt(Student::getId));
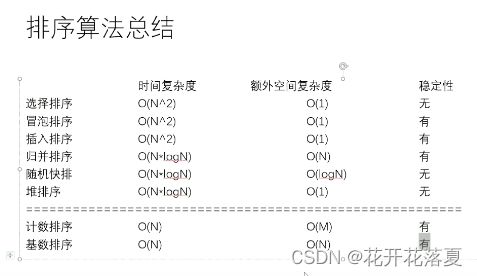
5.排序算法总结
(1)稳定性
稳定性是指同样大小的样本在排序之后,不会改变相对次序
对基础类型来说,稳定性没有意义(因为基础类型是按值传递)
但对非基础类型来说,稳定性有重要意义(当非基础类型,对多个指标进行排序时,若算法有稳定性,则多个指标排序后,内部其他指标也是有序的,否则无序)
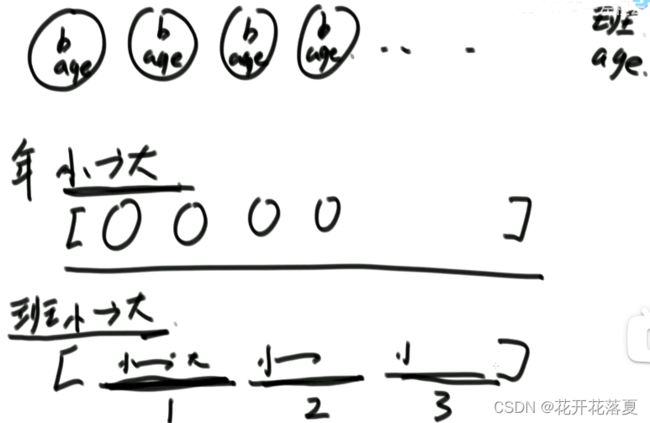
有些排序算法可以实现成具有稳定的,但有些排序算法无法实现
冒泡排序,插入排序,相等时不交换,可以实现稳定排序;归并排序,相等时先插入左边的值,可以实现稳定排序
快速排序无法稳定,随机挑选tmp;堆不稳定,只在乎如何组成堆;
2.总结
(1)不基于比较的排序,对样本数据有严格的要求,不易改写
(2)基于比较的排序,只要规定好两个样本怎么比大小就可以直接复用
(3)基于比较的排序,时间复杂度的极限是O(NlogN)
(4)时间复杂度为O(NlogN),额外空间复杂度低于O(N),且稳定的基于比较的排序是不存的
(5)为了绝对的速度选快排,为了省空间选堆排,为了稳定性选归并