8-5交换排序-快速排序

partition [pɑːˈtɪʃn] 分割
pivot [ˈpɪvət] 枢轴
pivotpos(ition) 枢轴位置

一.基本思想
以某一元素作为枢轴，使得其左边的元素都比他小，右边的元素都比他大。然后再递归的对左右两个部分处理。

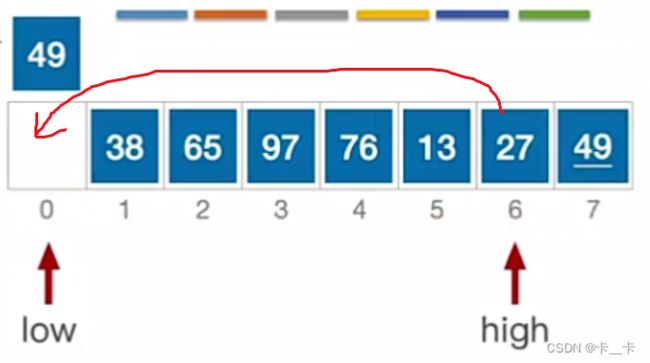
low和high分别指向首尾元素，初始值为0和7

以下从小到大排序，以49为枢轴/基准，用pivot记录49的值
代码：int pivot=a[low];

low和high都向中间移动，使得high右边都≥49，low左边都≤49

（一）第一轮
high指向的元素49≥枢轴pivot的49

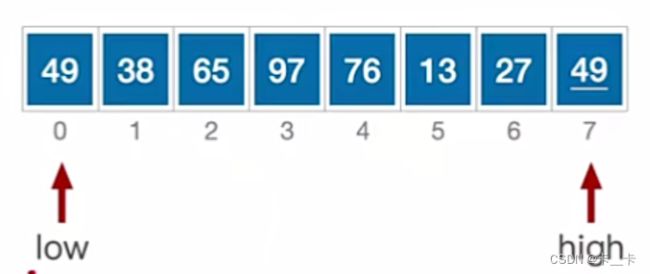
保持不变，high–，继续看high

while (pivot <= a[high]) 
	high--;

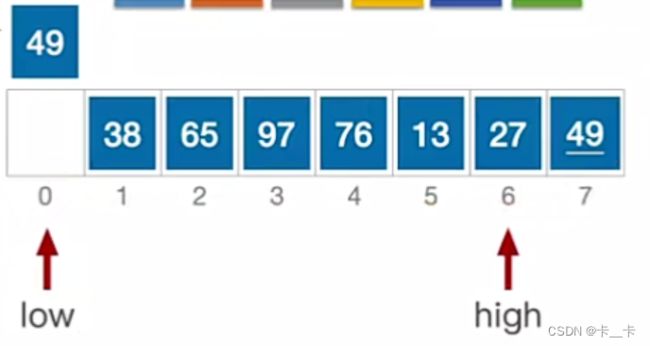
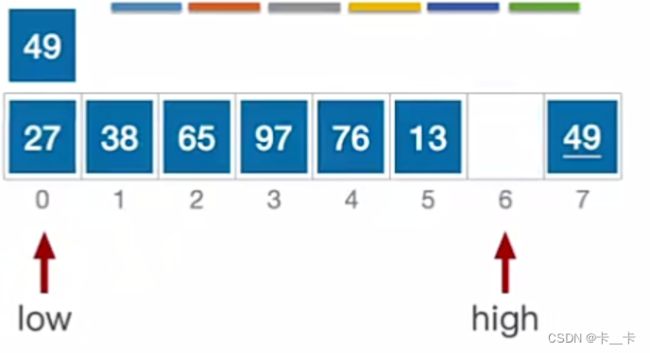
high所指元素27＜枢轴元素pivot=49，跳出while循环。将其放到low的位置，移动后转向看low

while (pivot <= a[high]) 
	high--;
a[low] = a[high];

即

low所指元素27≤49，不移动，low++

while (pivot >= a[low]) low++;

low所指元素38≤49，不移动，low++

while (pivot >= a[low]) 
	low++;

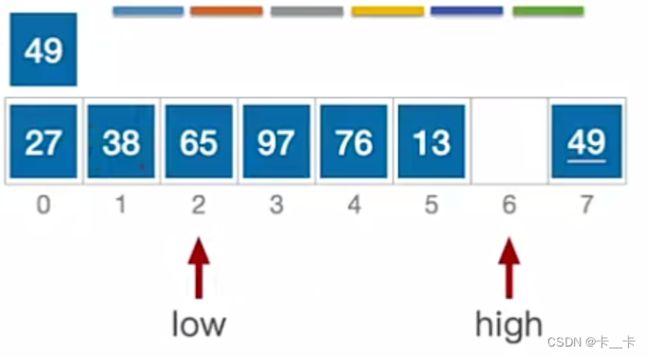
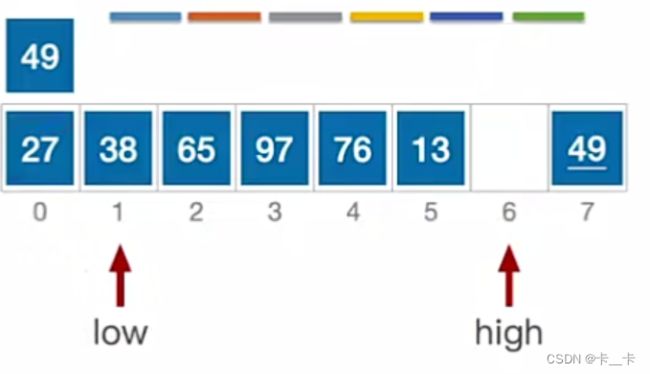
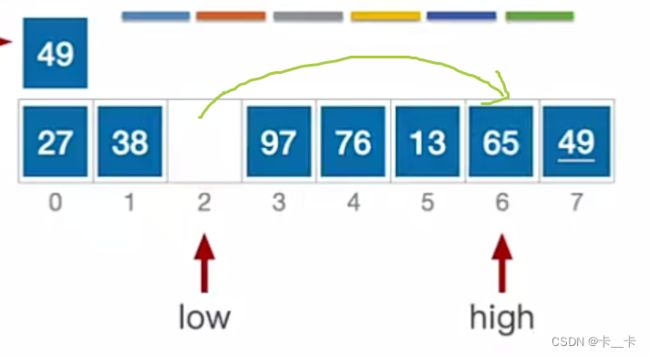
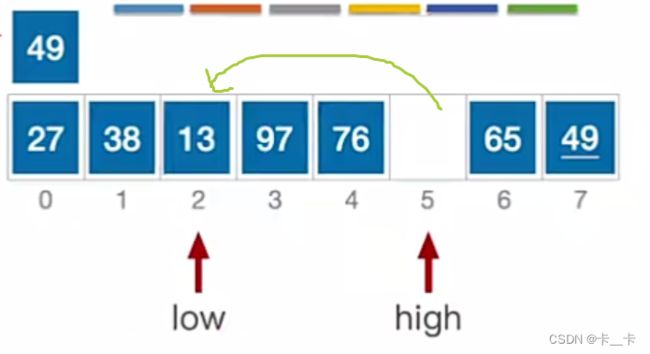
low指向元素65＞49，跳出while循环。放到high的位置，移动后转向看high

while (pivot >= a[low]) 
	low++;
a[high] = a[low];

high指向元素=65≥49，不移动，high–

while (pivot <= a[high]) 
	high--;

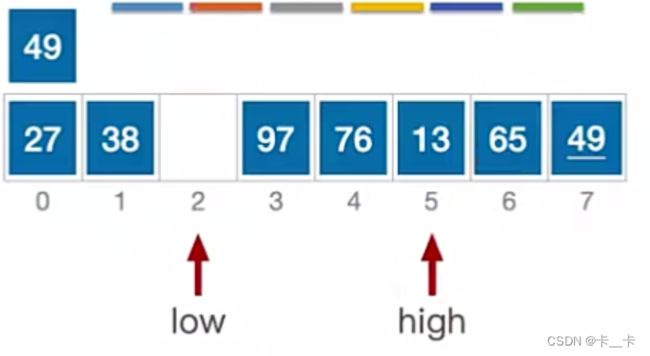
high指向元素13＜49，跳出while循环。移动，转向看low

while (pivot <= a[high]) 
	high--;
a[low] = a[high];

low指向13≤49，不移动，low++

while (pivot >= a[low]) 
	low++;

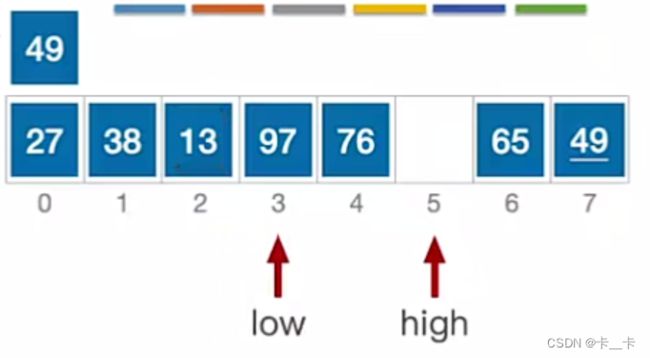
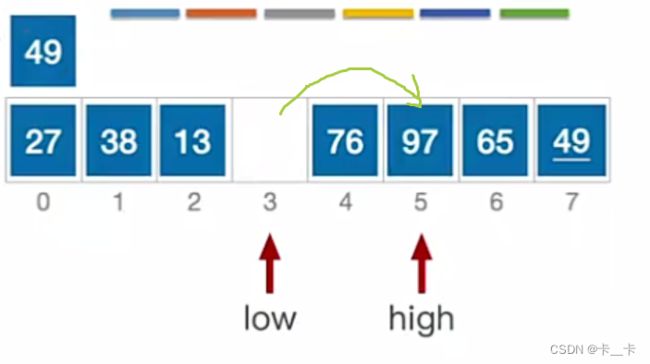
low指向元素=97＞49，跳出while循环。移动，转向看high

while (pivot >= a[low] && low < high) 
	low++;
a[high] = a[low];

high指向元素=97≥49，high–

while (pivot <= a[high]) 
	high--;

high=76≥49，high–

while (pivot <= a[high]) 
	high--;

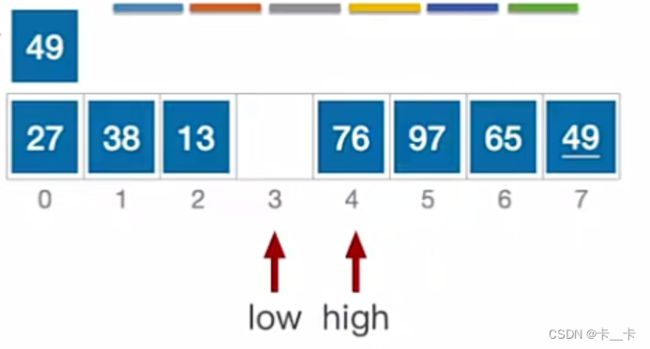
当low=high时，将枢轴元素49放入low和high所指位置

a[low] = pivot;

第一轮结束

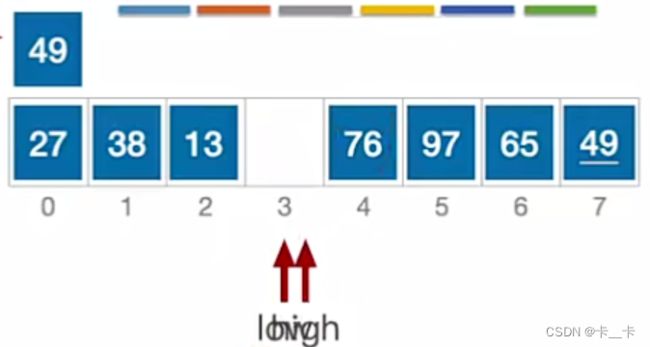
此时左边元素都比49小（或等），右边元素都比49大（或等）

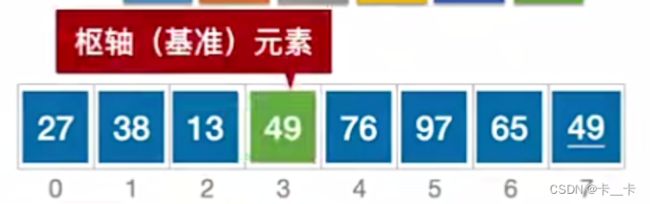
第一轮结束确定了一个元素的最终位置

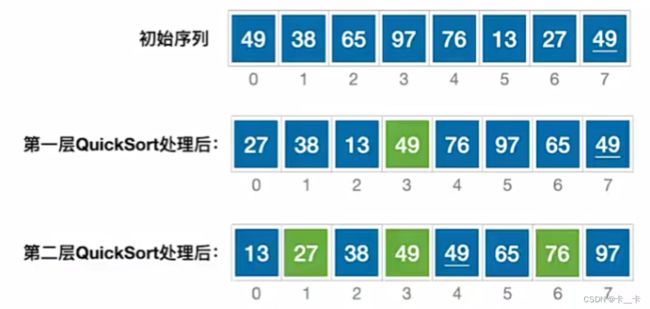
（二）第二轮
对左边部分0-2（即low到枢轴-1）和右边部分4-7（即枢轴+1到high）做同样的处理


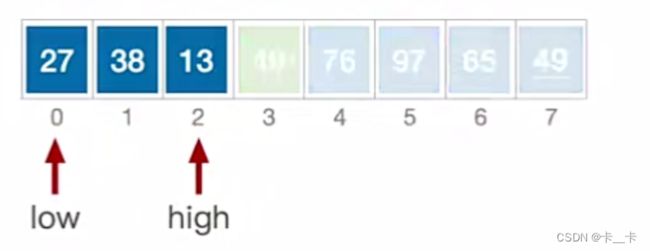
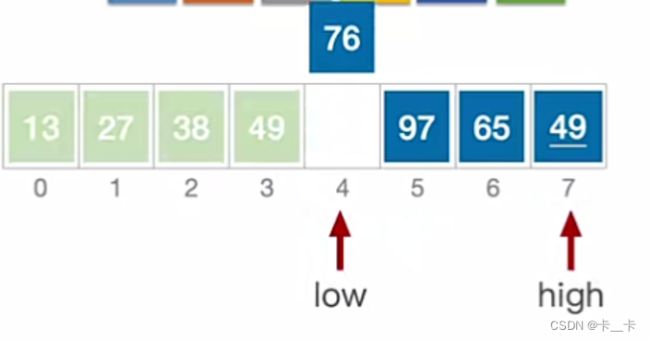
第二轮结束后，确定了3个元素的最终位置

注：
一次划分≠一趟排序
1.一趟排序：对所以未确定最终位置的元素进行一遍处理（左右两端都处理），可能确定多个元素的最终位置
2.一次划分：对指定的low和high的连续一段进行排序（只处理一端），只能确定一个元素的最终位置

以此类推，此例子一共需要四轮完成排序

二.代码表示

#include
#include
using namespace std;
int Partition(int a[], int low, int high)//根据传进来的low和high进行当前轮的排序和分割
{
	int pivot=a[low];
	while (low < high)
	{
		while (pivot <= a[high]&&low<high) //注意限制low
			high--;
		a[low] = a[high];
		while (pivot >= a[low] && low < high) 
			low++;
		a[high] = a[low];
	}
	a[low] = pivot;
	return low;//记录第i轮结束后枢轴的位置，便于QuickSort中取pivotpos±1
}
void QuickSort(int a[], int low, int high)
{
	if (low < high)
	{
		int pivotpos = Partition(a, low, high);//pivotpos表示当前枢轴的位置
		QuickSort(a, low, pivotpos - 1);//左边部分排序
		QuickSort(a, pivotpos + 1, high);//右边部分排序
	}
}
int main()
{
	int a[5] = {34,23,12,87,45 };
	QuickSort(a, 0,4);//low=0，high=4
	for (int i = 0; i < 5; i++)
	{
		cout << a[i] << " ";
	}
}

三.效率分析
1.时间复杂度
Partition函数的low和high向中间逼近的过程，每一轮的处理都不会超过O(n)，时间复杂度为O(n×递归层数)
2.空间复杂度
需要借助递归工作栈，空间复杂度=O(递归层数)

3.进一步分析




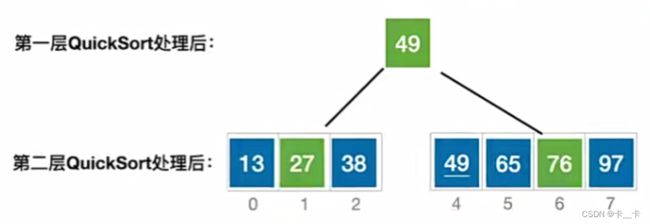
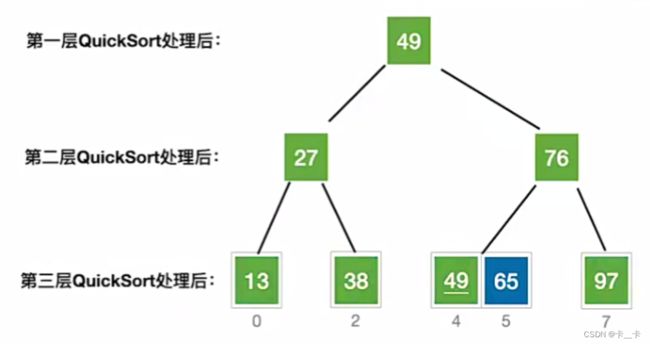
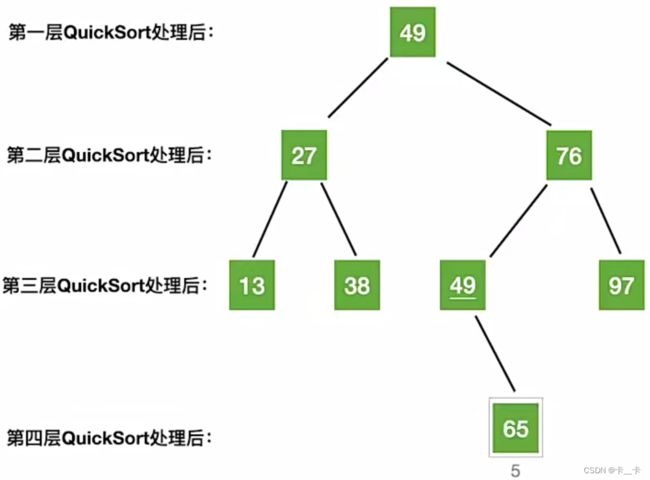
可以看出，二叉树的层数就是递归调用的层数
而二叉树的$h_{min}$=⌊$lo{g}_2$n⌋，$h_{max}$=n

因此
（1）最好/平均时间复杂度=O(n×递归层数)=O(n$lo{g}_2$n)
最坏时间复杂度=O(n×递归层数)=O(n²)
（2）最好空间复杂度=O($lo{g}_2$n)
最坏空间复杂度=O(n)

4.若每次选中的枢轴将待排序序列划分为均匀的两个部分，则递归深度最小，算法效率最高

如果初始基本有序（顺序/逆序），第一轮结束后，作为枢轴0号位的1还在原来的位置，当做pivotpos进一步划分时，左侧没有元素，待排序序列分布不均匀，后面同理，因此此时效率最低

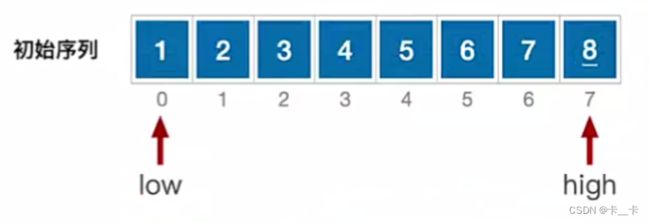
5.提高效率的方法：选择合适的枢轴
（1）从头、中、尾三个位置取中间值作为枢轴
（2）随机选

6.稳定性

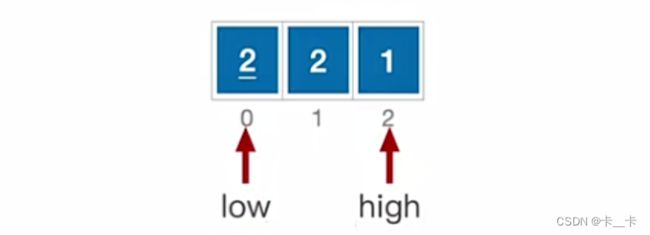
1移过去

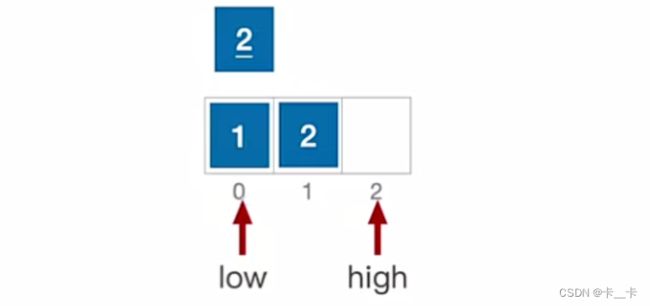
low++

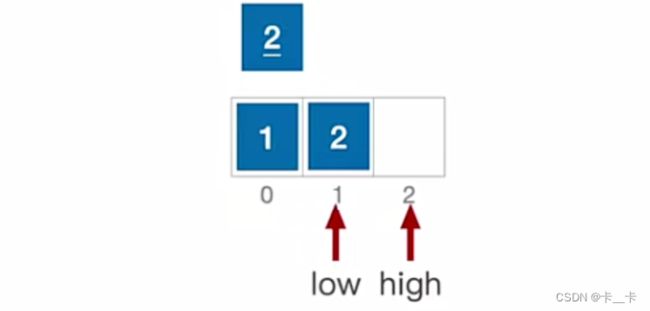
low++

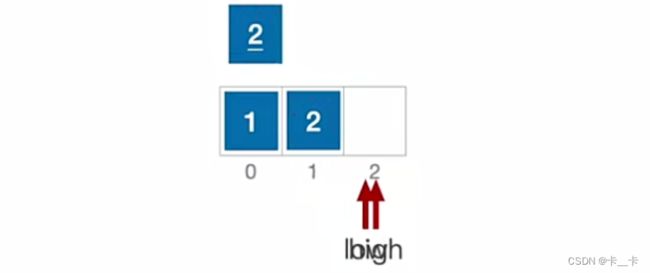
此时low=high，2插入，可以看出2和2的顺序发生了变化，因此快速排序是不稳定的

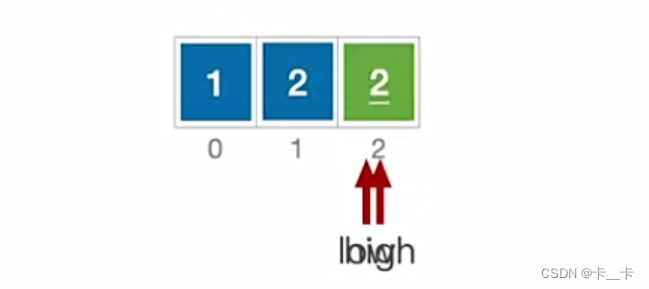
四.总结