【路径规划】基于遗传算法求解水面艇避碰问题附matlab代码
1 内容介绍
为减轻船舶驾驶人员在海上工作的负担和避免避碰过程中的操作失误,可利用现代化的科学手段和方法进行智能决策。大数据、互联网、人工智能等技术和理论的快速发展为船舶智能避碰决策的研究提供了强有力的技术和硬件支撑。船舶避碰路径规划是实现船舶智能避碰决策的关键技术之一,它经过大半个世纪的发展,从早期的经典数学理论逐渐过渡到基于人工智能和学科交叉的路径规划研究,取得了一定的研究成果。TAM等将避碰路径规划的研究方法归纳为确定性算法和启发式算法:确定性算法是遵循一定的计算流程来确定最终方案的,主要包括专家系统、模糊逻辑、人工势场法等;启发式算法是在一个搜索区域的子空间内寻找一个滿足设计要求的优化方案的,主要包括遗传算法、蚁群算法、粒子群优化算法等。不同方法具有各自独特的优势,但都存在一定的缺陷。例如:专家系统的重点是建立避碰知识库和推理机制,可是存在知识获取困难,完备、简练的知识库难以形成,系统实时性较差,智能学习的能力不具备等问题;虽然模糊逻辑在船舶避碰领域的应用能在一定程度上实现对避碰这种非确定性问题的推理,但模糊推理的输出依赖于事先设定的参数,目前对模糊控制量的设定均使用经验参数,对环境因素考虑较少,环境自适应性有待提高基于人工势场法对船舶进行避碰决策具有计算简洁、实时性强、便于数学描述等优点,但是存在局部极小值导致的陷阱区域、在碍航物前发生振荡、在邻近碍航物间不能发现路径等固有缺陷。用确定性算法对船舶避碰路径进行规划的特点是计算量小、收敛速度快,但是往往基于其他变量确定的假设对某一变量进行确定,实际上船舶避碰路径规划是一个包含避碰规则、动态障碍避让、船舶操纵性能等多方面的决策优化问题。因此,很多专家学者转向基于启发式算法的船舶避碰路径规划研究,取得了一定的研究成果。然而启发式算法经常存在早熟收敛的问题,致使得到的决策方案不符合要求,因此采用不同的混合方式对各种技术进行优势互补以获得求解能力更强的路径规划模型成为一种新的趋势。
遗传算法具有对可行解编码的广泛性和易于与其他人工智能技术混合等特点,在船舶避碰路径规划领域受到广泛关注。本文基于遗传算法和非线性规划理论建立船舶避碰路径规划模型,解决遗传算法的早熟收敛问题,使混合后的算法在性能和效率方面都得到提高,为驾驶员的避碰决策提供科学依据和支撑。
2 仿真代码
%
function rep=DeleteOneRepMemebr(rep,gamma)
% Grid Index of All Repository Members
GI=[rep.GridIndex];
% Occupied Cells
OC=unique(GI);
% Number of Particles in Occupied Cells
N=zeros(size(OC));
for k=1:numel(OC)
N(k)=numel(find(GI==OC(k)));
end
% Selection Probabilities
P=exp(gamma*N);
P=P/sum(P);
% Selected Cell Index
sci=RouletteWheelSelection(P);
% Selected Cell
sc=OC(sci);
% Selected Cell Members
SCM=find(GI==sc);
% Selected Member Index
smi=randi([1 numel(SCM)]);
% Selected Member
sm=SCM(smi);
% Delete Selected Member
rep(sm)=[];
end
function z=MultiObj(x,Curren,Waypoint,Obs)
global MAX_VAL;
global v;
%v=3;
G=abs(x(1)-Curren.angle);
Curren.angle=x(1);
Turnpot.x=Curren.posx+v*x(2)*cos(-(Curren.angle-pi/2));
Turnpot.y=Curren.posy+v*x(2)*sin(-(Curren.angle-pi/2));
if ((Waypoint.y-Turnpot.y)>0)
angle2=atan((Waypoint.x-Turnpot.x)/(Waypoint.y-Turnpot.y));
else
angle2=atan((Waypoint.x-Turnpot.x)/(Waypoint.y-Turnpot.y))+pi;
end
if (angle2<=0)
angle2=angle2+2*pi;
end
Curdis1=zeros(Obs.num,1);
Curdis2=zeros(Obs.num,1);
Distowayp=sqrt((Waypoint.x-Curren.posx)^2+(Waypoint.y-Curren.posy)^2);
CPA1=MAX_VAL*ones(Obs.num,2);
CPA2=MAX_VAL*ones(Obs.num,2);
DCPA=MAX_VAL*ones(Obs.num,1);
f=ones(Obs.num,1);
for i=1:Obs.num
Curdis1(i)=sqrt((Curren.posx-Obs.xCurren(i))^2+(Curren.posy-Obs.yCurren(i))^2);
% Curdis1(i)=pdist([Curren.posx,Curren.posy; Obs.xStar(i),Obs.yStar(i)],'euclidean');
% Curdis2(i)=pdist([Turnpot.x,Turnpot.y; Obs.xStar(i),Obs.yStar(i)],'euclidean');
[CPA1(i,:)]=CalcuCPA(Curren,Curdis1(i), Obs.xCurren(i), Obs.yCurren(i),Obs.speed(i),Obs.angle(i));
Curren2.posx=Turnpot.x;
Curren2.posy=Turnpot.y;
Curren2.speed=v;
Curren2.angle=angle2;
Obs.xCurren(i)=Obs.xCurren(i)+Obs.speed(i)*x(2)*cos(-(Obs.angle(i)-pi/2));
Obs.yCurren(i)=Obs.yCurren(i)+Obs.speed(i)*x(2)*sin(-(Obs.angle(i)-pi/2));
Curdis2(i)=sqrt((Turnpot.x-Obs.xCurren(i))^2+(Turnpot.y-Obs.yCurren(i))^2);
[CPA2(i,:)]=CalcuCPA(Curren2,Curdis2(i), Obs.xCurren(i), Obs.yCurren(i),Obs.speed(i),Obs.angle(i));
if (CPA1(i,2)<0)
DCPA(i)=Curdis1(i);
else
DCPA(i)=CPA1(i,1);
end
if (CPA2(i,2)<0)
DCPA(i)=min(DCPA(i),Curdis2(i));
else
DCPA(i)=min(DCPA(i),CPA2(i,1));
end
if (DCPA(i)>=Obs.rmin(i))
f(i)=Obs.rmin(i)-DCPA(i);
elseif (DCPA(i)
end
end
F=max (f); % safety objective
%G=pi-(x(1)-Curren.angle)-atan((v*x(2)*sin(x(1)-Curren.angle))/(Distowayp-v*x(2)*cos(x(1)-Curren.angle))); % maximum curvature
G=G+abs(angle2-x(1));
T=x(2)+(1/v)*pdist([Turnpot.x,Turnpot.y; Waypoint.x,Waypoint.y],'euclidean'); % total time
% if ((v-Curren.speed)==0)
% P=0;
% else
% P=1;
% end
%z=[F;G;P];
z=[F;G;T];
%[DCPA, TCPA]=calcuCPA(Curren,Curdis,ObsPosx,ObsPosy)
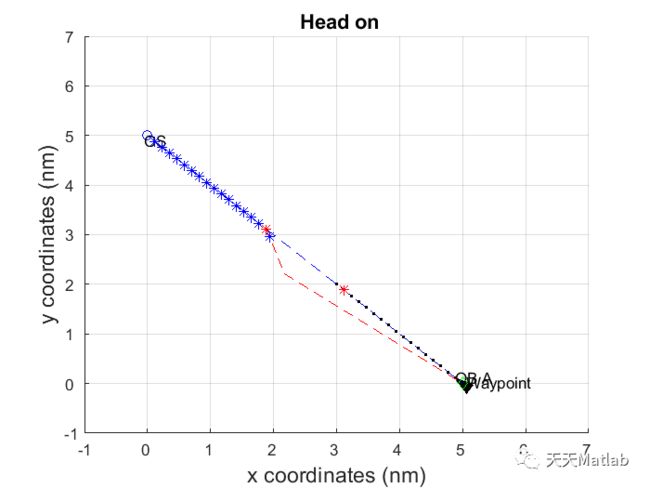
3 运行结果
4 参考文献
[1]刘渐道, 刘文, 张英俊,等. 基于改进动态窗口法的无人水面艇自主避碰算法[J]. 上海海事大学学报, 2021, 42(2):7.
[2]苏金涛. 无人水面艇路径规划[J]. 指挥控制与仿真, 2015, 37(6):5.
[3]倪生科, 刘正江, 蔡垚,等. 基于混合遗传算法的船舶避碰路径规划[J]. 上海海事大学学报, 2019.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。