数论专题1

update 2021 2.18 14.56 更新欧拉定理 和 一道欧拉定理 + 同余的题

1.欧拉晒
2.二次筛法
3.快速进行质因数分解
4.求约数的个数
5.筛法求欧拉函数
6.扩展欧几里得算法
7.欧拉定理
8.中国剩余定理
9.高斯消元
10.FFT
11.线性基
12.矩阵乘法
13.余数之和 小 trick
14.NTT
15.整除分块sqrt(n)
16.从1异或到n (o1)
17.卢卡斯定理

首先是欧拉筛 我就不是做说明了

#include

using namespace std;

const int N = 1e6 + 10;

int prime[N],flag[N],cnt;

void is_prime(){
	for(int i = 2; i <= N - 1; i++){
		if(!flag[i]){
			flag[i] = 1;
			prime[++cnt] = i;
		}
		for(int j = 1; i * prime[j] <= N - 1; j++){
			flag[i * prime[j]] = 1;
			if(i % prime[j] == 0){
				break;
			}
		}
	}
}

二次筛法

因为数据很大 L,U >=1 <= 1e9 但是LU的差距不超过1e6
所以用欧拉筛肯定是超时的
所以我们用二次筛法
因为一定存在一个质数属于sqrt(n)
所以我们只需要筛出sqrt(n) 然后将属于LU内的质数筛掉即可

#include
#include
#include

using namespace std;

const int N = 1e6 + 10;

int prime[N],flag[N],cnt;

typedef long long ll;

void is_prime(){
	for(int i = 2; i <= N - 1; i++){
		if(!flag[i]){
			flag[i] = 1;
			prime[++cnt] = i;
		}
		for(int j = 1; i * prime[j] <= N - 1; j++){
			flag[i * prime[j]] = 1;
			if(i % prime[j] == 0){
				break;
			}
		}
	}
}

int main(){
	
	is_prime();
	ll l,r;
	while(cin >> l >> r){
		memset(flag,0,sizeof flag);
		if(l == 1) flag[0] = 1;
		for(int i = 1; i <= cnt; i++){
			int p = prime[i];
			if(sqrt(r) < prime[i]) break;
			for(ll j = max((l + p - 1) / p * p,2ll * p); j <= r; j += p){
				flag[j - l] = 1;
			}
		}
		ll maxn = 0,minn = 1e9;
		ll s1 = -1,s2 = -1;
		
		ll last = -1;
		for(ll i = l; i <= r; i++){
			if(!flag[i - l]){
				if(last == -1){
					last = i;
					continue;
				}else{
					if(maxn < i - last){
						maxn = i - last;
						s1 = i;
					}
					if(minn > i - last){
						minn = i - last;
						s2 = i;
					}
					last = i;
				}
			}
		}
		
		if(s1 == -1 && s2 == -1){
			printf("There are no adjacent primes.\n");
		}else{
			printf("%d,%d are closest, %d,%d are most distant.\n",s2 - minn,s2,s1 - maxn,s1);
		}
	}
	
	
	
	
	
	return 0;
}

快速进行阶层质因数分解

其次是讲讲如何快速的进行阶层的质因数分解
正确的数学姿态是:我们发现N!中质数因子p的个数,就是1~N中每个数含有的质因数p个数.既然如此的话,那么我们发现,至少有一个质因子p的显然有[n/p]个,而至少有两个质因子p数的显然是有 [n/p^2]

比如8！找2的因子的次数
由于是8 就有 4个2的倍数 2 4 6 8 所以 +4
有2个4的倍数 4 8
有一个8的倍数 8
所以总体2的次数即为4+2+1 = 7

#include
#include
#include

using namespace std;

const int N = 1e6 + 10;

int prime[N],flag[N],cnt,num[N];

typedef long long ll;

void is_prime(int n){
	for(int i = 2; i <= n; i++){
		if(!flag[i]){
			flag[i] = 1;
			prime[++cnt] = i;
		}
		for(int j = 1; i * prime[j] <= n; j++){
			flag[i * prime[j]] = 1;
			if(i % prime[j] == 0){
				break;
			}
		}
	}
}

int main(){
	

	
	int n;
	cin >> n;
		is_prime(n);
	for(int i = 1; i <= cnt; i++){
		int h = n,p = prime[i],ans = 0;
		while(h){
			ans += (h / p);
			h /= p;
		}
		cout << prime[i] << " " << ans << endl;
	}
	
	
	
	
	return 0;
}

约数的个数

欧拉函数！

筛法求欧拉函数

void isprime(int n){
    phi[1] = 1;
    for(int i = 2; i <= n; i++){
        if(!flag[i]){
            prime[++cnt] = i;
            phi[i] = i - 1; //由于i为质数 所以与前i - 1个数互质
        } 
        for(int j = 1; prime[j] * i <= n; j++){
            flag[i * prime[j]] = 1;
            if(i % prime[j] == 0) {
                phi[i * prime[j]] = phi[i] * prime[j]; 
        //因为i 有prime[j]的因子了 由欧拉函数定理n = p1^a1 * p2^a2...*pn^an  s(n) = p1-1/p1..*pn-1/pn 所以只需要再乘上prime[j]即可
                break;
            }
            phi[i * prime[j]] = phi[i] * (prime[j] - 1); //因为没有prime[j]这个因子所以要乘上prime[j] 然后 *(prime[j] - 1)/prime[j] 所以整体就是乘上prime[j] - 1;
        }
    }
    return;
}

扩展欧几里得算法 求同余

1. 求任意一组ax + by = gcd(x,y)的解

#include
using namespace std;
int exgcd(int a,int b,int &x,int &y){
    if(b == 0){
        x = 1,y = 0;
        return a;
    }
    int x1,y1;
    int gcd = exgcd(b,a % b,x1,y1);
    x = y1,y = x1 - a / b * y1;
    return gcd;
}
int main(){
    int t;
    cin >> t; int x,y,a,b;
    while(t--){
        cin >> a >> b;
        exgcd(a,b,x,y);
        cout << x << " " << y << endl;
    }
    return 0;
}

2.ax + by = m 求任意一组x，y
只有 m % gcd(x,y) == 0 才有解

#include
using namespace std;
int exgcd(int a,int b,int &x,int &y){
    if(!b){
        x = 1,y = 0;
        return a;
    }
    int x1,y1,gcd;
    gcd = exgcd(b,a % b,x1,y1);
    x = y1,y = x1 - a / b * y1;
    return gcd;
}
int main(){
    int t;
    cin >> t;
    while(t--){
        int a,b,m,x,y,gcd;
        cin >> a >> b >> m;// ai * xi = bi - mi * yi;
        gcd = exgcd(a,m,x,y);
        if(b % gcd != 0) cout << "impossible" << endl;
        else cout <<1ll *  x * b / gcd % m << endl;
    }
    return 0;
}

3.求ax同余c(modb) 最小整数解
由于通解为 x = x1 + k * c / d；// c为同余后面的那个数 d为最小公倍数 k为1.2.3.。。。n； x1 = x0 * c / d; ax0 + by0 = 1；
所以求最小整数解需要 为 (x1 % (c / d) + c / d) % (c / d)；

#include
using namespace std;
int exgcd(int a,int b,int &x,int &y){
    if(!b){
        x = 1,y = 0;
        return a;
    }
    int x1,y1,gcd;
    gcd = exgcd(b,a % b,x1,y1);
    x = y1,y = x1 - a / b * y1;
    return gcd;
}
int main(){
    int t;
        int a,b,m,x,y,gcd;
        cin >> a >> m;// ai * xi = bi - mi * yi;
        b = 1;
        gcd = exgcd(a,m,x,y);
        m = m / gcd;
        cout << (1ll *  x * b / gcd + m) % m << endl;
    return 0;
}

欧拉定理
由百度百科推到可得
a ^ [φ(n)]≡1 （mod n）
当n 为质数时 φ(n) = n - 1
所以费马小定理得证 a ^ [n - 1]≡1 （mod n）

acwing 202的题目
如下推导

所以只需要求出 10^n 与 1同余 9L/d
n即为φ(9L/d)
由于题目是求最小的值 而欧拉定理并没有说 φ(9L/d)是最小值
由唯一分解定理可得 只有当 φ(9L/d)|K 的时候 K才可能为最小值
所以我们只需要 再遍历 φ(9L/d)的约数 即可

#include
#include

using namespace std;

typedef long long ll;

ll get_euler(ll c){
	ll s = c;
	for(int i = 2; i * i <= c; i++){
		if(c % i == 0){
			while(c % i == 0) c/= i;
			s = s / i * (i - 1);
		}
	}
	if(c > 1) s = s / c * (c - 1);
	return s;
}

ll qc(ll a,ll b,ll c){
	ll s = 0;
	while(b){
		if(b & 1) s = (s + a) % c;
		b >>= 1;
		a = (a + a) % c;
	}
	return s;
}

ll qmi(ll a,ll b,ll c){
	ll s = 1;
	while(b){
		if(b & 1) s = qc(s,a,c);
		b >>= 1;
		a = qc(a,a,c);
	}
	return s;
}
int main(){
	ll L;
	int t = 0;
	while(cin >> L && L){
		ll d = __gcd(9 * L,8ll);
		ll c = 9 * L / d;
		
		ll phi = get_euler(c);
		
		ll res = 1e18;
		if(c % 2 == 0 || c % 5 == 0) res = 0;
		else{
			for(ll d = 1; d * d <= phi; d++){
				if(phi % d == 0){
					if(qmi(10,d,c) == 1) res = min(res,d);
					if(qmi(10, phi / d, c) == 1) res = min(res, phi / d);
				}
			}
		}
		printf("Case %d: %lld\n",++t,res);
	}
	
	
	return 0;
}

中国剩余定理

由百度百科可知最后的推导公式为

mi即为除了第i个m的其余m的乘积
ti为mi的逆元

#include

using namespace std;

typedef long long ll;

const int N = 15;
ll a[N],b[N];

ll exgcd(ll a,ll b,ll &x,ll &y){
	if(!b){
		x = 1,y = 0;
		return a;
	}
	ll x1,gcd;ll y1;
	gcd = exgcd(b,a % b,x1,y1);
	x = y1,y = x1 - a / b * y1;
	return gcd;
}

int main(){
	int n;
	cin >> n;
	ll M = 1;
	for(int i = 1; i <= n; i++){
		cin >> a[i] >> b[i];
		M *= a[i];
	}
	
	ll x = 0;
	for(int i = 1; i <= n; i++){
		ll t,y;
		ll m = M / a[i];
		ll gcd = exgcd(m,a[i],t,y); //因为a[i]互相互质所以m与a[i]也互质
		//所以所求t即为m的逆元
		x += b[i] * m * t;
	}
	
	cout << (x % M + M) % M << endl;
	
	
	return 0;
} 

中国剩余定理扩展 ax1 = b1 (mod c1) ax2 = b2 (modc2) 且 ‘c1 c2 互不互素都可用
这篇文章通俗易懂

#include
#include

using namespace std;

typedef long long ll;

ll exgcd(ll a,ll b,ll &x,ll &y){
	if(!b){
		x = 1,y = 0;
		return a;
	}
	ll x1,gcd,y1;
	gcd = exgcd(b,a % b,x1,y1);
	x = y1,y = x1 - (a / b) * y1;
	return gcd;
}

int main(){
	int n;
	cin >> n;
	ll a1,b1,a2,b2;
	cin >> a1 >> b1;
	bool flag = 1;
	for(int i = 2; i <= n; i++){
		cin >> a2 >> b2;
		ll d = __gcd(a1,a2);
		ll x,y;
		ll gcd = exgcd(a1 / d,a2 / d,x,y);
		if((b2 - b1) % d!= 0){
			flag = 0;
			break;
		}
		
		b1 = (x * (b2 - b1) / d) % (a2 / d) * a1 + b1;
		a1 = (a1 * a2) / d;
		b1 = (b1 % a1 + a1) % a1;
	}
	
	cout << (flag?b1:-1) << endl;
	
	return 0;
} 

高斯消元

高斯消元 就是利用矩阵行列式变换来解n个n元等式
行列式的形式：

由这张图可以看 1.任意一个等式两边同时乘上一个数解不会变
2.任意一个等式 + 上k倍另一个等式 解不会变
3.交换他们的顺序 解也不会变
如何求解 就要使矩阵成为上三角的形式

这根斜线以下的都为0
求解成这个形式后从下往上消元即可
总体步骤是 1.找到当前列绝对值最大的一行
2.将当前行的一个的系数变为1
3.下面每一行的这一列的系数变为0
4.从下往上利用下面行 的已知数求解上面行的未知``

tips：若当前行已经为 0 = 0则这一行放到最下面求解下面一行
如果 是个完美三角 即 x0 ~ xn都有准确数字 则有唯一解
若没有 则为无数个解
若 求解出 左式 ！= 右式 即为 无解

#include
#include

using namespace std;

const int N = 110;
const double eps = 1e-6;

double a[N][N];

int n;

int guess(){
	int c,r;
	for(c = 1,r = 1;c <= n; c++){
		int t = r;
		for(int i = r; i <= n; i++){
			if(fabs(a[i][c]) > fabs(a[t][c])) t = i;
		}
		
		if(fabs(a[t][c]) < eps) continue;
		
		for(int i = c; i <= n + 1; i++) swap(a[t][i],a[r][i]);
		for(int i = n + 1; i >= c; i--){
			a[r][i] /= a[r][c];
		}
		
		for(int i = r + 1; i <= n; i++){
			if(fabs(a[i][c]) > eps){
				for(int j = n + 1; j >= c; j--){
					a[i][j] -= a[r][j] * a[i][c];
				}
			}
		}
		
		r++;
	}

	if(r <= n){
		for(int i = r; i <= n + 1; i++){
			if(fabs(a[i][n + 1]) > eps) return 2; //无解 
		}
		return 1;//多个解 
	}
	
	for(int i = n; i >= 1; i--){
		for(int j = i + 1; j <= n; j++){
			a[i][n + 1] -= a[j][n + 1] * a[i][j];
		}
	}
	
	return 0;
}

int main(){
	cin >> n;
	
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= n + 1; j++){
			cin >> a[i][j];
		}
	}
	
	int t = guess();
	
	if (t == 0){
        for (int i = 1; i <= n; i ++ ) printf("%.2lf\n", a[i][n + 1]);
    }
    else if (t == 1) puts("Infinite group solutions");
    else puts("No solution");
	
	
	
	return 0;
}

n3的辗转反测法

#include
#include

using namespace std;

typedef long long ll;

const int N = 400;
const double eps = 1e-6;

ll a[N][N];

int n,p;

void kill(ll a,ll b,ll &aii,ll & aij,ll &aji,ll &ajj,ll &pa){
    pa = 1;
	aii = ajj = 1;
	aji = aij = 0;
	while(b){
		aii -= a / b * aji;
		aij -= a / b * ajj;
		aii = (aii % p + p) % p;
		aij = (aij % p + p) % p;
		a %= b;
		swap(a,b);
		swap(aii,aji);
		swap(aij,ajj);
		pa = -pa;
	}
	return;
}

ll guess(){
    ll ret = 1,_a,b,c,d,s1,s2,pa;
    for(int i = 1; i <= n; i++){ //当前列
        for(int j = i + 1; j <= n; j++){
        	kill(a[i][i],a[j][i],_a,b,c,d,pa);
        	ret *= pa;
        	for(int k = 1; k <= n; k++){
        		s1 = (a[i][k] * _a + a[j][k] * b) % p;
        		s2 = (a[i][k] * c + a[j][k] * d) % p;
        		a[i][k] = s1,a[j][k] = s2;
        	}
        }
        if(a[i][i] == 0) return 0;
        ret = ret * a[i][i] % p;
    }

    return (ret + p) % p;
}

int main(){
    while(~scanf("%lld%lld",&n,&p)){
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= n; j++){
                scanf("%lld",&a[i][j]);
            }
        }

        printf("%lld\n",(guess() + p) % p);
    }



	return 0;
}

FFT 模板
求解 多项式

就是求卷积

#include
#include

using namespace std;

const int N = 300010;
const double PI = acos(-1);

int bit,rev[N],tot;

struct Complex{
	double x,y;
	Complex operator + (const Complex &t){
		return {x + t.x,y + t.y};
	}
	Complex operator - (const Complex &t){
		return {x - t.x,y - t.y};
	}
	Complex operator * (const Complex &t){
		return {x * t.x - y * t.y,x * t.y + y * t.x};
	}
}a[N],b[N];

void fft(Complex a[],int inv){
	for(int i = 0; i < tot; i++){
		if(i < rev[i]){
			swap(a[i],a[rev[i]]); // 因为二进制取反 所以交换 
		}
	} 
	
	for(int mid = 1; mid < tot; mid <<= 1){
		auto w1 = Complex({cos(PI / mid),inv * sin(PI / mid)});// 分为mid份 中得第一份
		for(int i = 0; i < tot; i += mid * 2){
			auto wk = Complex({1,0});
			for(int j = 0; j < mid; j++,wk = wk * w1){ //wk每次+一份得值 
				auto x = a[i + j],y = wk * a[i + j + mid];
				a[i + j] = x + y,a[i + j + mid] = x - y;
			}
		} 
	} 
}

int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i = 0; i <= n; i++){
		scanf("%lf",&a[i].x);
	}
	
	for(int i = 0; i <= m; i++){
		scanf("%lf",&b[i].x);
	}
	
	while((1 << bit) < n + m + 1) bit++;
	tot = 1 << bit;
	
	for(int i = 0; i < tot; i++){
		rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
	}
	
	fft(a,1),fft(b,1);
	for(int i = 0; i < tot; i++){
		a[i] = a[i] * b[i];
	}
	fft(a,-1);
	for(int i = 0; i <= n + m; i++){
		printf("%d ", (int)(a[i].x / tot + 0.5));
	}

	return 0;
} 

线性基
这是一种利用高斯消元的思想去求 一组基底 使得基底 的张成是所有数

#include
#include

using namespace std;

const int N = 1e4 + 10;

typedef long long ll;

ll a[N];

int n,k = 0;
void work(){ //预处理 基底
	for(int i = 62; i >= 0; i--){
		for(int j = k; j < n; j++){
			if(a[j] >> i & 1){
				swap(a[j],a[k]);
				break;
			}
		}
		if(!(a[k] >> i & 1)) continue;
		for(int j = 0; j < n; j++){
			if(j != k && (a[j] >> i & 1)){
				a[j] ^= a[k];
			}
		}
		++k;
		if(k == n) break;
	}
	reverse(a,a + k);
}

ll k_th(ll x){ //第小大
	if(k < n) --x;
	ll ans = 0;
	if(x >= (1ll << k)) return -1;
	else{
		for(int i = 0; i < k; i++){
			if(x >> i & 1){
	  			ans ^= a[i];
			}
		}
	}
	return ans;
}

ll get_max(ll x){
	ll ans = 0;
	for(int i = k - 1; i >= 0; k--){
		ans ^= a[i];
	}
	return ans;
}

int main(){
	int t;
	cin >> t;
	int cas = 0;
	while(t--){
		scanf("%d",&n);
		for(int i = 0; i < n; i++){
			scanf("%lld",&a[i]);
		}
		k = 0;
		
		work();
		
		printf("Case #%d:\n",++cas);
		int q;
		cin >> q;
		for(int i = 1; i <= q; i++){
			ll x;
			scanf("%lld",&x);
			printf("%lld\n",k_th(x));
		}
	}

	return 0;
}

矩阵乘法
找到转移式
然后利用矩阵快速幂

#include
#include
#define endl "\n"

using namespace std;

typedef long long ll;

ll n,m;

ll a[4][4];
ll b[4][4];

void muti(ll a[][4],ll b[][4]){
	ll temp[4][4] = {0};
	for(int i = 1; i <= 3; i++){
		for(int j = 1; j <= 3; j++){
			temp[i][1] += a[j][1] * b[i][j] % m;
			temp[i][1] %= m;
		}
	}
	for(int i = 1; i <= 3; i++){
		a[i][1] = temp[i][1];
	}
}

void mutic(ll a[][4],ll b[][4]){
	ll temp[4][4] = {0};
	for(int i = 1; i <= 3; i++){
		for(int j = 1; j <= 3; j++){
			for(int k = 1; k <= 3; k++){
				temp[i][j] += a[i][k] * b[k][j] % m;
				temp[i][j] %= m;
			}
		}
	}
	
	for(int i = 1; i <= 3; i++){
		for(int j = 1; j <= 3; j++){
			a[i][j] = temp[i][j];
		}
	}
}

void qm(ll n){
	while(n){
		if(n & 1){
			muti(a,b);
		}
		n >>= 1;
		mutic(b,b);
	}
}

int main(){
	cin >> n >> m;
	a[1][1] = 2;
	a[2][1] = 1;
	a[3][1] = 0;
	b[1][1] = 2;
	b[1][3] = -1;
	b[2][1] = 1;
	b[3][2] = 1;
	
	if(n >= 2)
	qm(n - 2);
	
	cout << (a[1][1] + m) % m << endl;
	
	
	
	return 0;
} 

余数之和
n % 1 + n % 2 +…+ n % n; n数据最大为1e12
首先 n % m = n - n / m * m
所以和为 n * n - sigema(1,n) n / m * m;
数据很大我们考虑分块解决
由于 当 商为 1 2 3 这种数的时候 n / 1 ~ n / 2 + 1，n / 2 ~ n / 3 + 1中间有很多数 所以我们处理这些数只需要利用整除分块来求就行 商为 sqrn(n) ~ n 只有sqrt（n) 个数 只需要on遍历即可
总体只需要 2 sqrt(n)即可完成

#include
#include

using namespace std;

typedef long long ll;

const int N = 1e6,mod = 1e9 + 7;

ll n,sum;

int main(){
    cin >>n;
    ll s = sqrt(n);
    for(int i = 1; n / i > s; i++){
        sum = sum + n / i * i;
        sum %= mod;
    }

    for(int i = 1; i <= s; i++){
        ll l = n / i,r = n / (i + 1) + 1;
        l %= mod,r %= mod;
        sum = sum + (((1ll * i * 500000004) % mod) * ((l + r) % mod) % mod) * (l - r + 1) % mod;
        sum %= mod;
    }

    sum = (n % mod) * (n % mod) % mod - sum;
    sum %= mod;
    sum = sum + mod;
    sum %= mod;
    cout << sum << endl;

    return 0;
}

#include
#define maxn 2000050
#define modu 998244353
using namespace std;
typedef long long LL;

LL pw(LL a,LL k=modu-2) {
    LL ans=1;
    for (;k;k>>=1) {
        if (k&1)
            ans=ans*a%modu;
        a=a*a%modu;
    }
    return ans;
}

namespace NTT   {
    int rev[maxn],N;
    LL w[maxn],I;
    void init(int n) {
        for (N=1;N<=n;N<<=1); I=pw(N);
        
        rev[0]=0,rev[1]=N>>1;
        for (int i=2;i<N;++i) rev[i]=rev[i>>1]>>1|rev[i&1];

        w[0]=1,w[1]=pw(3,(modu-1)/N);
        for (int i=2;i<N;++i) w[i]=w[i-1]*w[1]%modu;
    }

    void DFT(LL *A) {
        for (int i=0;i<N;++i)
            if (i<rev[i])
                swap(A[i],A[rev[i]]);
        
        for (int len=2;len<=N;len<<=1)  {
            int m=len>>1;
            for (LL *p=A;p!=A+N;p+=len)
                for (int i=0;i<m;++i)   {
                    LL u=p[i],v=p[i+m]*w[N/len*i]%modu;
                    p[i]=(u+v)%modu;
                    p[i+m]=(u-v+modu)%modu;
                }
        }
    }

    void IDFT(LL *A)    {
        DFT(A);
        reverse(A+1,A+N);
        for (int i=0;i<N;++i)
            A[i]=A[i]*I%modu;
    }
}

const int w=5e5+10;

int n;
LL A[maxn],B[maxn];

int main()  {
    scanf("%d",&n);
    for (int i=0,a;i<n;++i)   {
        scanf("%d",&a);
        A[a]=1;
        B[w-a]=1;
    }
    
    NTT::init(w*2+5);
    NTT::DFT(A);
    NTT::DFT(B);
    for (int i=0;i<NTT::N;++i)
        A[i]=A[i]*B[i]%modu;
    NTT::IDFT(A);

    // for (int i=1;i<=w;++i)
    //     if (A[i+w])
    //         cout<

    for (int i=1;i<=w;++i)  {
        int flag=0;
        for (int j=i;j<=w;j+=i)
            flag|=A[j+w];
        if (!flag)  {
            printf("%d\n",i);
            break;
        }
    }
    return 0;
}

15.整出分块

sqrt(n)复杂度求出下述公式

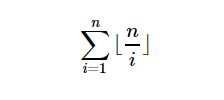
l 为起点 r即为 n / (n / l)

1异或到 n (o1)

ll xors(ll n){
    ll t = n & 3;
    if(t & 1) return t / 2u ^ 1;
    return t / 2u ^ n;
}

卢卡斯定理
若预处理在 p 里面 那么就是 p + logp m
若不是则是 plogp m

#include
#include

using namespace std;

const int N = 1e5 + 10;

int fac[N];

void init(int p){
    fac[0] = 1;
    for(int i = 1; i <= 1e5; i++){
        fac[i] = 1ll * fac[i - 1] * i % p;
    }
}

int qpow(int a,int b,int p){
    int s = 1;
    while(b){
        if(b & 1) s = 1ll * s * a % p;
        a = 1ll * a * a % p;
        b >>= 1;
    }
    return s;
}

int cal(int x,int y,int p){
    if(y > x) return 0;
    return 1ll * fac[x] * qpow(fac[y],p - 2,p) % p * qpow(fac[x - y],p - 2,p) % p;
}

int lucas(int x,int y,int p){
    if(!y) return 1;
    return 1ll * cal(x % p,y % p,p) * lucas(x / p,y / p,p) % p;
}

int main(){
    int t;
    cin >>t;
    while(t--){
        int n,m,p;
        cin >> n >> m >> p;
        init(p);

        cout << lucas(n + m,n,p) <<endl;
    }






    return 0;
}