数据挖掘之K近邻算法分类和KD树改进及代码超详细

需要资料QQ1271370903

一、

1.分类算法

KNN(K-Nearest Neighbor即K近邻),监督学习算法。
当预测一个新的值x的时候，根据它距离最近的K个点是什么类别来判断属于哪个类别。做分类也可以做回归。

2.原理说明：

最简单最初级的分类器是将全部的训练数据所对应的类别都记录下来，当测试对象的属性和某个训练对象的属性完全匹配时，便可以对其进行分类。但是怎么可能所有测试对象都会找到与之完全匹配的训练对象呢，其次就是存在一个测试对象同时与多个训练对象匹配，导致一个训练对象被分到了多个类的问题，基于这些问题呢，就产生了KNN。
KNN是通过测量不同特征值之间的距离进行分类。它的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中K通常是不大于20的整数。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

3.图例引入

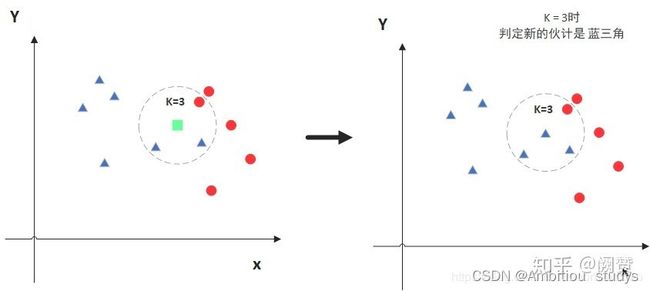
图中绿色的点就是我们要预测的那个点，假设K=3。那么KNN算法就会找到与它距离最近的三个点（这里用圆圈把它圈起来了），看看哪种类别多一些，比如这个例子中是蓝色三角形多一些，新来的绿色点就归类到蓝三角了。

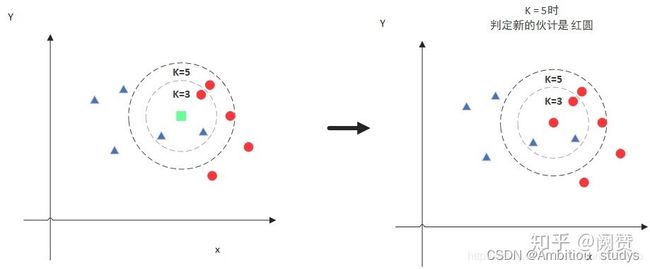
但是，当 K=5 的时候，判定就变成不一样了。这次变成红圆多一些，所以新来的绿点被归类成红圆。从这个例子中，我们就能看得出 K 的取值是很重要的。
由此也说明了KNN算法的结果很大程度取决于K的选择。

4.距离计算

在KNN中，通过计算对象间距离来作为各个对象之间的非相似性指标，欧氏距离euclidean、曼哈顿距离manhattan、马氏距离、切比雪夫距离chebyshev等等，避免了对象之间的匹配问题，在这里距离一般使用欧氏距离或曼哈顿距离：

拿二维平面为例，二维空间两个点的欧式距离计算公式如下：

拓展到多维空间，则公式变成这样：

KNN算法最简单粗暴的就是将预测点与所有点距离进行计算，然后保存并排序，选出前面K个值看看哪些类别比较多。

5.KNN算法的描述为：

1）计算测试数据与各个训练数据之间的距离；
2）按照距离的递增关系进行排序；
3）选取距离最小的K个点；
4）确定前K个点所在类别的出现频率；
5）返回前K个点中出现频率最高的类别作为测试数据的预测分类。

6.K值选择

通过图例引入我们知道K的取值比较重要，那么该如何确定K取多少值好呢？答案是通过交叉验证（将样本数据按照一定比例，拆分出训练用的数据和验证用的数据，比如6：4拆分出部分训练数据和验证数据），从选取一个较小的K值开始，不断增加K的值，然后计算验证集合的方差，最终找到一个比较合适的K值。当增大K的时候，一般错误率会先降低，因为有周围更多的样本可以借鉴了，分类效果会变好。但注意，和K-means不一样，当K值更大的时候，错误率会更高。这也很好理解，比如说你一共就35个样本，当你K增大到30的时候，KNN基本上就没意义了。所以选择K点的时候可以选择一个较大的临界K点，当它继续增大或减小的时候，错误率都会上升。

二、

1.优点、缺点和适用范围

优点：原理简单，易于理解，没有高深的数学理论；没有假定条件，适合类域交叉样本、适用范围广;受异常值的影响小，适用大样本自动分类;重新训练代价低，算法复杂度低。
缺点：样本不平衡问题（即有些类别的样本数量很多，而其它样本的数量很少）效果差；需要大量内存；对于样本容量大的数据集计算量比较大（体现在距离计算上）；样本不平衡时，预测偏差比较大。如：某一类的样本比较少，而其它类样本比较多；KNN每一次分类都会重新进行一次全局运算；k值大小的选择没有理论选择最优，往往是结合K-折交叉验证得到最优k值选择。
适用范围：文本分类、模式识别、聚类分析，多分类领域

2.KNN的改进方案

一是优化决策方式，采用加权距离，二是提高搜索近邻点的速度，利用KD树快速定位近邻点（主要分析改进这种）。
（1）加权距离
找出k个近邻点之后，直接投票决策未必准确。这样就等同于认为各近邻点对待测点有一样的影响力。但是一般来说，待测点应该更“像”离它近的样本点，更“不像”较远的样本点。这就需要对距离值进一步分析了，给近点加大权重，同时减少远点的决策影响力。有两种反函数和高斯函数。无论是采用哪种加权方案，都要注意加权曲线不要急剧衰减。否则，容易错误地增大了噪声的影响力，又无法给正确样本点赋予足够的权重，令算法对噪声太敏感，出现1个噪声点“打败”N个正确样本的尴尬。
（2）KD树（k-dimensional tree）
如果每次使用KNN算法，都要遍历所有的训练集样本数据，还需要计算新的实例点与样本点距离，选择与新实例点最近的K个训练样本点，根据多数表决规则判断新实例点属于那个类别，如果给定训练集的N非常大，成千上百，上万上亿，这时计算量非常大，而且如果训练数据集样本点特征很多，成千上万特征距离就更麻烦了，实际上绝大部分样本点都不需要参与决策。可以快速搜索方法，可以构建KD树来实现。
KD树类似于二叉排序树，是一种数据结构，用来提升查询数据的效率。先来回顾一下二叉排序树的性质：
若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值。
简单总结：小的放左边，大的放右边。
1）说明
KD树是一种对K维空间中的实例点进行存储以便对其进行快速检索的树形数据结构.
本质；二叉树，表示对K维空间的一个划分。
构造过程：不断地用垂直于坐标轴的超平面将K维空间切分，形成K维超矩形区域。
KD树的每一个结点对应于一个K维超矩形区域。

二维空间的划分

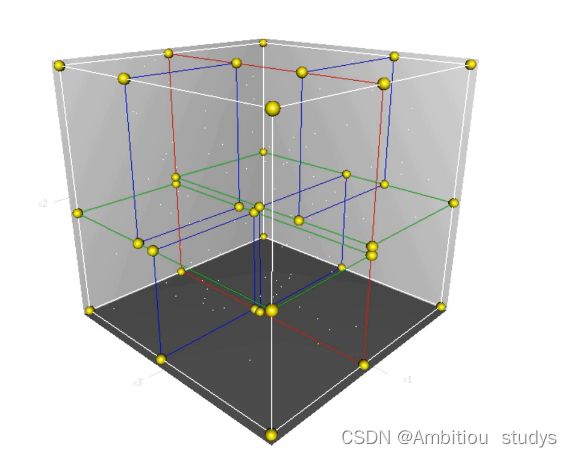
三维空间的划分
2)构造方法如下：
训练集：一堆拥有标签的m维数据，可以表示为：
其中 ， 是标签，即所属类别。
目标：一个测试数据x，预测其所属类别。
1.选取为坐标轴，以训练集中的所有数据坐标中的中位数作为切分点，将超矩形区域切割成两个子区域。将该切分点作为根结点，由根结点生出深度为1的左右子结点，左节点对应坐标小于切分点，右结点对应坐标大于切分点
2.对深度为j的结点，选择为切分坐标轴，，以该结点区域中训练数据坐标的中位数作为切分点，将区域分为两个子区域，且生成深度为j+1的左、右子结点。左节点对应坐标小于切分点，右结点对应坐标大于切分点
3.重复2直到两个子区域没有数据时停止。
3)例题演示
输入：训练集
T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}
输出：KD树

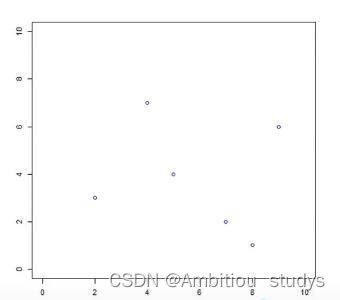
图上 图下
X(1):2,4,5,7,8,9
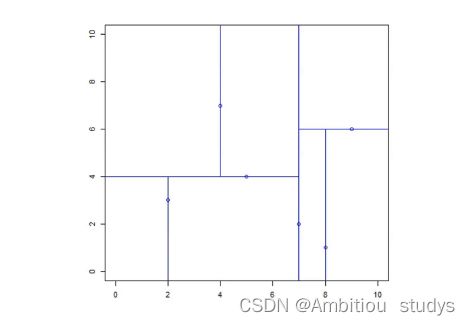
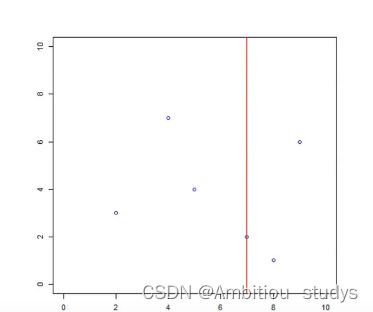
开始:选择x(1)为坐标轴，中位数为7，即(7,2)为切分点，切分整个区域(图上)

再次划分区域:
以x(2)为坐标轴，选择中位数，左边区域为4，右边区域为6。故左边区域切分点为(5,4)，右边区域切分点坐标为(9,6)（图下）
同理最后

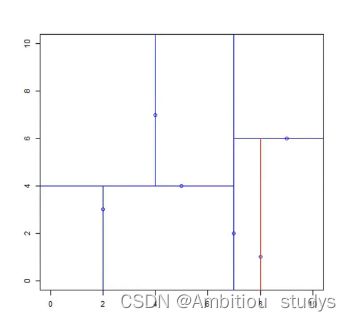
3）搜索KD树（最近邻搜索）


寻找“当前最近点”：寻找最近邻的子结点作为目标点的“当前最近点”。
回溯：以目标点和“当前最近点”的距离沿树根部进行回溯和迭代。
算法
输入:已构造的kd树，目标点×
输出:x的最近邻
寻找“当前最近点”
----从根结点出发，递归访问kd树，找出包含x的叶结点;
----以此叶结点为“当前最近点”;
回溯
—若该结点比“当前最近点”距离目标点更近，更新“当前最近点”;
—当前最近点一定存在于该结点一个子结点对应的区域，检查子结点的父结点的另一子结点对应的区域是否有更近的点。
当回退到根结点时，搜索结束，最后的“当前最近点”即为×的最近邻点。
输入;KD树，目标点x=(2.1,3.1)
图一
最近邻点为（2，3）

输入;KD树，目标点x=(2,4.5)
图二
最近邻点为（2，3）

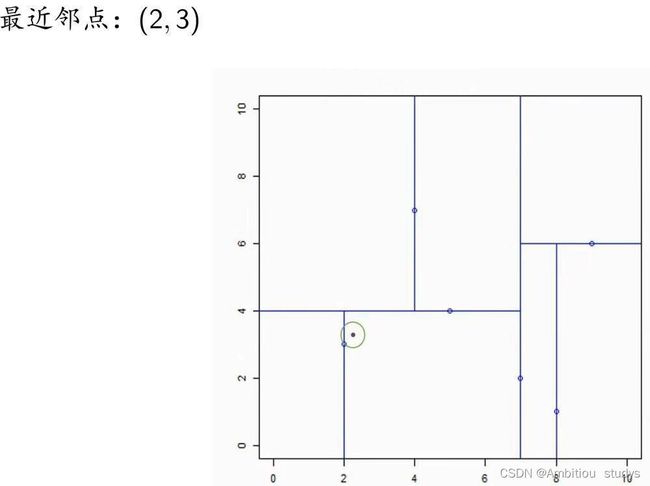
图一 第一次回溯（2，3）结束

图二 第一次回溯
图二 第二次回溯近邻点（2，3），搜索结束

3.原来与改进后对比

（1）数据预处理，即将点的坐标转换为二维数组。np.concatenate进行矩阵合并，axis=1指定横向合并
spots = np.concatenate([np.array(df[‘x.1’]).reshape(-1, 1),
np.array(df[‘x.2’]).reshape(-1, 1)],axis=1)
（2）散点图，看一下数据分布

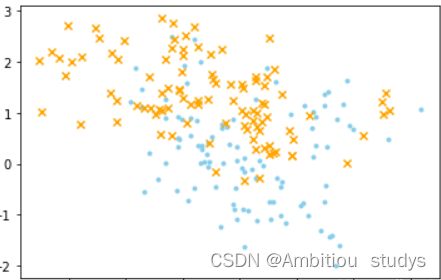
（3）利用python实现KNN，这里我们计算点之间的欧式距离

def take_nearest(grid, k):
	对传入的点进行 knn 分类
	:param grid: 点的坐标
	:type grid : tuple
	:param k: 邻居个数
	:type k : int
	:return : 点的分类
   	# 计算所有已知点距离未知点的距离，即实现 欧氏距离 的计算
    distance = np.sqrt(np.sum((spots - grid) ** 2, axis=1))
    # 类别判断
    cate = Counter(np.take(df['y'],distance.argsort()[:k])).most_common(1)[0][0]
return cate

三、代码实现

1.创建Node类，初始化

class Node(object):
    def __init__(self):
        self.father = None  #存储父节点
        self.left = None  #左节点
        self.right = None  #右节点
        self.feature = None  #特征
        self.split = None  #分割点

2.获取Node的各个属性

def __str__(self):
return "feature: %s, split: %s" % (str(self.feature), str(self.split))
3．获取Node的兄弟节点
def brother(self):
    if self.father is None:
        ret = None
    else:
        if self.father.left is self:
            ret = self.father.right
        else:
            ret = self.father.left
    return ret

4.创建KDTree类

class KDTree(object):  #初始化，存储根节点
    def __init__(self):
        self.root = Node()

5.获取KD-Tree属性

def __str__(self):
    ret = []
    i = 0
    que = [(self.root, -1)]
    while que:
        nd, idx_father = que.pop(0)
        ret.append("%d -> %d: %s" % (idx_father, i, str(nd)))
        if nd.left is not None:
            que.append((nd.left, i))
        if nd.right is not None:
            que.append((nd.right, i))
        i += 1
    return "\n".join(ret)

6.获取数组中位数的下标

def _get_median_idx(self, X, idxs, feature):
    n = len(idxs)
    k = n // 2
    col = map(lambda i: (i, X[i][feature]), idxs)
    sorted_idxs = map(lambda x: x[0], sorted(col, key=lambda x: x[1]))
    median_idx = list(sorted_idxs)[k]
    return median_idx

7.计算特征的方差（D(X) = E(X^2)-[E(X)]2）

def _get_variance(self, X, idxs, feature):
    n = len(idxs)
    col_sum = col_sum_sqr = 0
    for idx in idxs:
        xi = X[idx][feature]
        col_sum += xi
        col_sum_sqr += xi ** 2
    return col_sum_sqr / n - (col_sum / n) ** 2

8.选择特征：取方差最大的的特征作为分割点特征

def _choose_feature(self, X, idxs):
    m = len(X[0])
    variances = map(lambda j: (
        j, self._get_variance(X, idxs, j)), range(m))
    return max(variances, key=lambda x: x[1])[0]

9.分割特征：把大于、小于中位数的元素分别放到两个列表中

def _split_feature(self, X, idxs, feature, median_idx):
    idxs_split = [[], []]
    split_val = X[median_idx][feature]
    for idx in idxs:
        if idx == median_idx:
            continue
        xi = X[idx][feature]
        if xi < split_val:
            idxs_split[0].append(idx)
        else:
            idxs_split[1].append(idx)
    return idxs_split

10.建立KDTree：广度优先搜索的方式建立KD Tree，注意要对X进行归一化

def build_tree(self, X, y):
    X_scale = min_max_scale(X)
    nd = self.root
    idxs = range(len(X))
    que = [(nd, idxs)]
    while que:
        nd, idxs = que.pop(0)
        n = len(idxs)
        if n == 1:
            nd.split = (X[idxs[0]], y[idxs[0]])
            continue
        feature = self._choose_feature(X_scale, idxs)
        median_idx = self._get_median_idx(X, idxs, feature)
        idxs_left, idxs_right = self._split_feature(X, idxs, feature, median_idx)
        nd.feature = feature
        nd.split = (X[median_idx], y[median_idx])
        if idxs_left != []:
            nd.left = Node()
            nd.left.father = nd
            que.append((nd.left, idxs_left))
        if idxs_right != []:
            nd.right = Node()
            nd.right.father = nd
            que.append((nd.right, idxs_right))

11.搜索辅助函数：比较目标元素与当前结点的当前feature，访问对应的子节点。反复执行上述过程，直到到达叶子节点。

def _search(self, Xi, nd):
    while nd.left or nd.right:
        if nd.left is None:
            nd = nd.right
        elif nd.right is None:
            nd = nd.left
        else:
            if Xi[nd.feature] < nd.split[0][nd.feature]:
                nd = nd.left
            else:
                nd = nd.right
    return nd

12.欧氏距离计算目标元素与某个节点的欧氏距离，注意get_euclidean_distance这个函数没有进行开根号的操作，所以求出来的是欧氏距离的平方。

def _get_eu_dist(self, Xi, nd):
    X0 = nd.split[0]
    return get_euclidean_distance(Xi, X0)

13.超平面距离：计算目标元素与某个节点所在超平面的欧氏距离，为了跟11保持一致，要加上平方

def _get_hyper_plane_dist(self, Xi, nd):
    j = nd.feature
    X0 = nd.split[0]
    return (Xi[j] - X0[j]) ** 2

14.搜索函数搜索KD Tree中与目标元素距离最近的节点，使用广度优先搜索来实现。

def nearest_neighbour_search(self, Xi):
    dist_best = float("inf")
    nd_best = self._search(Xi, self.root)
    que = [(self.root, nd_best)]
    while que:
        nd_root, nd_cur = que.pop(0)
        while 1:
            dist = self._get_eu_dist(Xi, nd_cur)
            if dist < dist_best:
                dist_best = dist
                nd_best = nd_cur
            if nd_cur is not nd_root:
                nd_bro = nd_cur.brother
                if nd_bro is not None:
                    dist_hyper = self._get_hyper_plane_dist(
                        Xi, nd_cur.father)
                    if dist > dist_hyper:
                        _nd_best = self._search(Xi, nd_bro)
                        que.append((nd_bro, _nd_best))
                nd_cur = nd_cur.father
            else:
                break
    return nd_best

15.线性查找用“笨”办法查找距离最近的元素

def exhausted_search(X, Xi):
    dist_best = float('inf')
    row_best = None
    for row in X:
        dist = get_euclidean_distance(Xi, row)
        if dist < dist_best:
            dist_best = dist
            row_best = row
return row_best

16.main函数
主函数分为如下几个部分：(1)随机生成数据集，即测试用例;(2)建立KD-Tree;(3)执行“笨”办法查找;(4)比较“笨”办法和KD-Tree的查找结果.

def main():
    print("Testing KD Tree...")
    test_times = 100
    run_time_1 = run_time_2 = 0
    for _ in range(test_times):
        low = 0
        high = 100
        n_rows = 1000
        n_cols = 2
        X = gen_data(low, high, n_rows, n_cols)
        y = gen_data(low, high, n_rows)
        Xi = gen_data(low, high, n_cols)

        tree = KDTree()
        tree.build_tree(X, y)

        start = time()
        nd = tree.nearest_neighbour_search(Xi)
        run_time_1 += time() - start
        ret1 = get_euclidean_distance(Xi, nd.split[0])

        start = time()
        row = exhausted_search(X, Xi)
        run_time_2 += time() - start
        ret2 = get_euclidean_distance(Xi, row)

        assert ret1 == ret2, "target:%s\nrestult1:%s\nrestult2:%s\ntree:\n%s" \
            % (str(Xi), str(nd), str(row), str(tree))
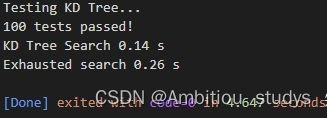
    print("%d tests passed!" % test_times)
    print("KD Tree Search %.2f s" % run_time_1)
    print("Exhausted search %.2f s" % run_time_2)

17.效果展示
随机生成了100个测试用例，线性查找用时0.26秒，KD-Tree用时0.14秒。