北邮新生排位赛4解题报告
<>
这次比赛打完....好像只有一个评价:你可以回家啦.....
A. 大家一起点外卖 2014新生暑假个人排位赛04
题目描述
大家都回了本部,本部生活虽然没有宏福天(mo)堂(gui)般的生活,但是却有很多外卖,今天有一家饭店新开张,凡是两个人的餐点费用之和刚好为m可以免运费,在今天一起点外卖且免运送费的两个人,各自点的外卖价格差值最小的有大惊喜。在机房的n个同学今天打算一起点外卖,但是每个人都只想要点某一个价格x的餐点,请你帮忙规划一下大家应当如何组合,并给出最有可能获得今天大惊喜的价格组合。
输入格式
第一行输入样例数
输出格式
如果能够找到最有可能获得今天大惊喜的价格组合,则输出两个人所点的餐点的价格,小的价格在前。
如果所有人都没办法免运送费,则输出“Sad”
输入样例
2
2 3
1
3
4 3
1
2
3
4输出样例
Sad
1 2我居然用的bool过,太水了....因为从来不愿意开大的数组.......
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cmath>
using namespace std;
int vis[2000001];
int money[500000];
int main(){
int t;
scanf("%d",&t);
for(int ti=1;ti<=t;ti++){
int n,m;
bool fl=false;
scanf("%d %d",&n,&m);
int mid=0;
for(int i=0;i<n;i++){
int temp;
scanf("%d",&temp);
vis[temp]=ti;
if((temp==m/2)&&(m-temp==temp)){
mid++;
if(mid>1)fl=true;
}
else money[i]=temp;
}
int maxans=0;
//sort(money1,money1+pm1);
if(!fl)for(int i=0;i<n;i++){
if(money[i]<=m/2){
if(vis[m-money[i]]==ti){
fl=true;
maxans=max(maxans,money[i]);
}
}
}
if(mid>1)maxans=m/2;
if(!fl)printf("Sad\n");
else printf("%d %d\n",maxans,m-maxans);
}
return 0;
}
B. 田田的公司 2014新生暑假个人排位赛04
题目描述
田田家开了一家大公司,面对现在的形势,很多公司选择了联盟。联盟一旦成立就意味着联盟内的每个公司互相之间都认可结盟。所以当决定以一家公司为对手的时候就一定要计算出这家公司所在联盟的总实力值来决定有没有能力击败对手。
现在有n个公司,和m条信息。每条信息可能是某两个公司宣布联盟或者查询某个公司所在联盟的实力值
输入格式
多组数据
第一行为数据量T,每个case第一输入n,m ,之后一行输入n个数ai表示第i个公司的实力值,之后m行输入信息,有两种信息
第一种为两个公司联盟,该行为1 x y ,1表示联盟操作,即x,y两个公司联盟,
第二种为查询某个公司,该行为2 x,2表示查询操作,即查询x公司所在联盟的实力值;
T<=10
n,m<=10^5
ai<=10^6
输出格式
每个查询一行输出,输出那个公司联盟的实力值
输入样例
1
5 5
1 2 3 4 5
1 1 2
2 2
2 5
1 2 3
2 1输出样例
3
5
6#include<cstdio>
using namespace std;
const int maxn=1000001;
int par[maxn];
long long cost[maxn];
int findpar(int i){
if(par[i]!=i){
cost[par[i]]+=cost[i];
//printf("par[%d]=%d\n",i,par[i]);
//printf("cost[%d]=%d\n",i,cost[i]);
cost[i]=0;
return (par[i]=findpar(par[i]));
}
else return i;
}
void uinon(int a,int b){
int ap=findpar(a);
// if(a!=par[a]&&cost[a])printf("ERROr");
int bp=findpar(b);
// if(b!=par[b]&&cost[b])printf("ERROr");
par[ap]=bp;
findpar(a);
}
int main(){
int t;
scanf("%d",&t);
while(t--){
int n,m;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)par[i]=i;
for(int i=1;i<=n;i++)scanf("%lld",cost+i);
while(m--){
int op;
scanf("%d",&op);
if(op==1){
int a,b;
scanf("%d %d",&a,&b);
uinon(a,b);
}
else {
int a;
scanf("%d",&a);
int p=findpar(a);
//for(int i=1;i<=n;i++)printf("par[%d]=%d\n",i,par[i]);
//for(int i=1;i<=n;i++)printf("cost[%d]=%d\n",i,cost[i]);
printf("%lld\n",cost[p]);
}
}
}
return 0;
}
439. 崔逗逗的难题
题目描述
崔逗逗放假回家后每天只能吃饭睡觉打豆豆感觉好无聊,该怎么给自己找找乐子呢?于是他主动去帮邻家初中小妹妹做作业。他看到了这样一道题:在一个边长为
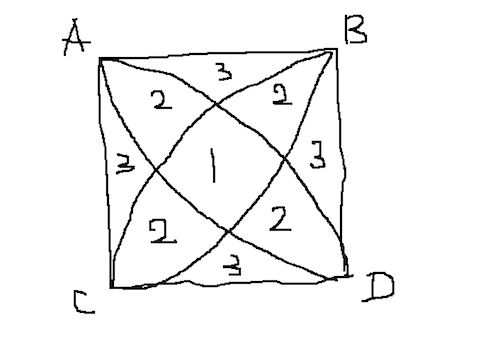
输入格式
多组数据。每组数据包含一个实数a,表示正方形的边长。
输出格式
对于每组数据,输出标号为1,2,3的图形面积。保留6位小数。
输入样例
0.2输出样例
0.012606 0.020452 0.006942#include<cmath>
#include <iostream>
#include<iomanip>
using namespace std;
int main(){
double a;
while(cin>>a){
double s3=(a*a*4.00-a*a*(acos(-1)*2/3.00)-a*a*sqrt(3.00));
double s2=(a*a*(acos(-1)/3.00)+a*a*2.00*sqrt(3.00)-a*a*4.00);
double s1=(a*a+a*a*acos(-1)/3.00-a*a*sqrt(3.00));
cout<<setiosflags(ios::fixed)<<setprecision(6)<<s1<<" "<<s2<<" "<<s3<<endl;
}
return 0;
}
435. 崔逗逗给你信心
题目描述
崔逗逗是一个善良的学长,最喜欢为学弟学妹出水题。他给大家一个整数n,求0<=x<=n的范围内,有多少个数满足(x)^(2x)^(3x)==0 (^是异或符号)。你只要告诉他对1000000009取余的答案就好啦。
输入格式
输入有多组数据,数量在100以内,每行一个整数n(0<=n<=10^18)。
输出格式
每组数据输出一行答案。
输入样例
1
2输出样例
2
3#include<cmath>
#include <cstring>
#include <string>
#include <iostream>
#include<iomanip>
using namespace std;
const int mod=1000000009;
long long f[62];
int digit[62];
int length(long long i){
int ans=0;
while(i!=0){
digit[ans++]=i&1;
i>>=1;
}
return ans;
}
int main(){
f[0]=1;
f[1]=2;
for(int i=2;i<62;i++){
f[i]=f[i-1]+f[i-2];
}
long long a;
while(cin>>a){
if(a==0)cout<<1<<endl;
// else if(a==1)cout<<2<<endl;
else {
long long ans=0;
int fl=0;
int len=length(a);
//cout<<"len "<<len<<endl;
for(int i=len-1;i>=0;i--){
//cout<<"i="<<i<<endl;
if(digit[i]){
ans=(ans+f[i])%mod;
//cout<<"+f["<<i-1<<"]"<<f[i-1]<<endl;
if(fl)break;
}
if(fl==0&&digit[i]&&i==0){
ans=(ans+1)%mod;
//cout<<"+f[0]\n";
}
else if(digit[i]==0&&i==0){
ans=(ans+1)%mod;
//cout<<"+f[0]\n";
}
fl=digit[i];
//cout<<"fl"<<fl<<endl;
}
cout<<ans<<endl;
}
}
return 0;
}
E:
434. 焦级长搭积木
题目描述
焦级长特别喜欢搭积木,一天他创造了一种新的玩法。焦级长一共有N个积木,从下往上一共搭了H层,其中最底层有M个积木,除最底层,每一层的积木数是它下一层积木数+1或-1且每层积木不超过10个。
输入格式
input 输入含多组数据。每组第一行为三个整数N,H,M,第二行后每行一个整数K,以-1结束(1<=N<=540,H<=60,M<=10,K<=10^10)。
输出格式
output 第一行是满足N、H、M的积木搭建方案总数,以后每一行对于对应的K,给出顺序排列的第K种方案(最小的排列为第一种)。 如样例中,2 1 2 3 2 3是一种方案,代表一层的积木数从下往上分别为212323,232321也是一种方案,212323比232321要小,即第一个数小的排前面,第一个数相等的就看第二个数,以此类推。 这里的K就是求第K个按顺序排列的方案。
输入样例
13 6 2
1
3
-1输出样例
3
2 1 2 3 2 3
2 3 2 3 2 1#include <iostream>
#include <assert.h>
#include <cstring>
using namespace std;
long long dp[61][11][541];//dp[H][M][N]
int N,H,M;
int store[61];
void findk(long long k){
int s=0,m=M,n=N;
store[0]=M;
n=N;
n-=m;
for(int i=H-1;i>0&&n>=0;i--){
if(m>1&&k<=dp[i][m-1][n]){
m=m-1;
}
else {
if(m>1)k-=dp[i][m-1][n];
m=m+1;
}
store[H-i]=m;
n-=m;
}
for(int i=0;i<H-1;i++){cout<<store[i]<<" ";}cout<<store[H-1]<<endl;
}
void printdp(){
for(int i=1;i<=H;i++){
for(int j=1;j<11;j++){
for(int k=1;k<=N;k++){
if(dp[i][j][k])cout<<"dp"<<"["<<i<<"]["<<j<<"]["<<k<<"]"<<dp[i][j][k]<<" ";
}
}
cout<<endl;
}
}
int main(){
while(cin>>N>>H>>M){
assert (N>0&&H>0&&M>0);
memset(dp,0,sizeof(dp));
for(int i=1;i<11;i++)dp[1][i][i]=1;
for(int i=1;i<H;i++){
for(int j=1;j<11;j++){
for(int k=1;k<=N;k++){
if(j>1&&k+j-1<=N)dp[i+1][j-1][k+j-1]+=dp[i][j][k];
if(j+1<11&&k+j+1<=N)dp[i+1][j+1][k+j+1]+=dp[i][j][k];
}
}
}
// printdp();
long long tk;
cout<<dp[H][M][N]<<endl;
while(cin>>tk&&tk!=-1){
if(dp[H][M][N]<tk){cout<<-1<<endl;continue;}
findk(tk);
}
}
return 0;
}