机器学习之神经网络-基础知识总结(第一篇)
文章目录
- 一、写在前面
- 二、关于线性回归与逻辑回归的知识回顾
-
- 1. 线性回归
- 2. 逻辑回归
- 三、人工神经网络基础
-
- 1. 从逻辑回归到神经网络
- 2. 神经元模型
- 3. 从单层感知机到多层感知机
- 4. 神经网络损失函数
- 5. 神经网络梯度计算
- 6. 前向传播与反向传播
一、写在前面
首先该文参考了一些博客与文章,在这对这些作者表达自己的敬意。其次本文主要聊一下自己对于神经网络的一些重新的理解,如果读者也有一些更好的观点,可以在评论区一起讨论学习。如果你已经理解了神经网络的知识或有一定的工作经验或只是想找一些更经典的人工神经网络算法(例如CNN、RNN、GAN、Transformers等等),那么我想这篇文章可能不太适合你,希望你可以找其它文章来寻求帮助。本文可能更适合了解一些线性回归和逻辑回归,并想继续学习神经网络基础但还未学习或不太理解的同学。
自己在下文中我尽可能将自己理解的与参考一些博客的知识详细的按照顺序介绍下来。
希望文章会有属于它自己的意义,对于自己也对于读者,以至于不浪费每个读者的时间。下面我们开始吧!
二、关于线性回归与逻辑回归的知识回顾
若是你已经了解线性回归与逻辑回归,读者可以跳过这部分,直接阅读第三部分。
1. 线性回归
什么是线性回归?
1. 维基百科:机器学习
在统计学中,线性回归(英语:linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析
2. 周志华:机器学习
基于均方误差最小化来进行模型求解的方法称为“最小二乘法”,线性回归中最小二乘法就是试图找到一条直线,使所有样本到直线上的欧氏距离之和最小。
简而言之,线性回归就是寻找一个线性方程,可以使我们的所有样本的结果值与其所对应线性方程的所计算出的值的均方误差达到最小。当我们采用一些减小误差的算法时,上面所计算的均方误差不再变化,那么就可以讲我们得到了一个线性回归模型。
训练线性回归模型需要的几个组成部分:
① 目标函数
何为目标函数?
目标函数就是我们根据处理过后的样本中的特征来假设的线性方程;样本的特征就是方程的变量;而我们方程中设定的变量系数与方程的常数项就是我们在优化该线性方程时需要修改的值,本文我们统一叫做待优化参数,通过修改该值来使其均方误差达到最小。下面举一个例子:
为了方便描述,下文中统一规定 Θ \Theta Θ 代表待优化参数的向量, X X X 代表变量的向量,上标 i i i 代表样本中第 i i i 行数据, j j j 代表第 j j j 个特征
假设我们要为房价作预测,一个房子可能有很多因素影响,我们选取其中的三个因素:房子的尺寸( x 1 x_1 x1)、房子包含的卧室数量( x 2 x_2 x2)、房子的层数( x 3 x_3 x3)。则上述的三个因素就是我们的特征,我们的样本中可能有很多关于这三个特征的数据。
那么我们根据上述的特征就是方程的变量,可以得到特征(方程变量)的向量 X = [ 1 x 1 x 2 x 3 ] (1) X=\left[ \begin{matrix} 1 \\ x_1 \\ x_2 \\ x_3 \end{matrix} \right]\tag{1} X=⎣ ⎡1x1x2x3⎦ ⎤(1)
其中上述特征向量中的 x 0 = 1 x_0=1 x0=1与代表方程的常数项。
根据上述的变量的系数与方程的常数项,我们叫做待优化参数,可以得到待优化参数的向量:
Θ = [ θ 0 θ 1 θ 2 θ 3 ] (2) \Theta=\left[ \begin{matrix} \theta_0 \\ \theta_1 \\ \theta_2 \\ \theta_3 \end{matrix} \right]\tag{2} Θ=⎣ ⎡θ0θ1θ2θ3⎦ ⎤(2)
则我们可以得到方程:
h θ ( x ) = Θ T X (3) h_\theta(x)=\Theta^TX\tag{3} hθ(x)=ΘTX(3)
其中(3)式也可以写出乘开形式:
h θ ( x ) = θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + θ 0 (4) h_\theta(x)=\theta_1x_1+\theta_2x_2+\theta_3x_3+\theta_0\tag{4} hθ(x)=θ1x1+θ2x2+θ3x3+θ0(4)
根据这个例子和(4)式方程的形式去尝试理解什么是目标函数。
注意:上面说何为目标函数概念地方,有一个说 我们根据处理后的样本中的特征…,这里的处理可能包括对影响较小的特征的裁减,也有对影响较大的特征操作成新特征的增加,也就是可能升维也可能降维,这对我们的目标函数是有影响的,所以我们需要先处理特征再设目标函数。当然我们也有不用手动降维和升维的更好的优化特征的方式,这里暂时不展开说了。
下面我们可以得到目标函数更一般的形式: X = [ 1 x 1 x 2 ⋮ x n ] X=\left[ \begin{matrix} 1 \\ x_1 \\ x_2 \\ \vdots \\ x_n \end{matrix} \right] X=⎣ ⎡1x1x2⋮xn⎦ ⎤
Θ = [ θ 0 θ 1 θ 2 ⋮ θ n ] \Theta=\left[ \begin{matrix} \theta_0 \\ \theta_1 \\ \theta_2 \\ \vdots \\ \theta_n \end{matrix} \right] Θ=⎣ ⎡θ0θ1θ2⋮θn⎦ ⎤
根据(3)式可得:
h θ ( x ) = θ 1 x 1 + θ 2 x 2 + . . . . . + θ n x n + θ 0 h_\theta(x)=\theta_1x_1+\theta_2x_2+.....+\theta_nx_n+\theta_0 hθ(x)=θ1x1+θ2x2+.....+θnxn+θ0
② 损失函数
损失函数是表达我们预测值与样本真实结果值之间的差距,当然为了增大或者缩小差距,使得差距的大或小更加明显(如果差距小于1,平方后会更小,如果大于1,平方后会更大,这样区分的会更加明显),另一方面也便于求导,通常取预测值与真实值的平方,再除以样本数量,即我们上面讲的均方误差。于是可以定义出损失函数 J ( θ ) J(\theta) J(θ):
J ( θ ) = 1 2 m ( ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 ) (5) J(\theta)=\frac{1}{2m}(\sum_{i=1}^{m}{(h_\theta(x^{(i)})-y^{(i)})}^2)\tag{5} J(θ)=2m1(i=1∑m(hθ(x(i))−y(i))2)(5)
关于上面的式子有以下说明:
由于训练时都是一组样本【其中 i i i 代表样本编号】(一组样本包含多个样本,每个样本都会有函数预测值和真实值),所以 m m m 就是代表本次训练的样本数量,该函数代表含义是将该组样本所有的预测值与真实值的差距的平方相加并除以2倍的的样本数量,相当于求平均误差。有趣的是除以 2 m 2m 2m 为的是后面求导方便。(求导会出来一个2,这样可以约分掉)
③ LMS 算法
在上面的公式中,我们想要找到能将 J ( θ ) J(\theta) J(θ)最小化的 θ \theta θ。我们可以使用一种搜索算法,该算法从先对 θ \theta θ进行“初始猜测”,并反复改变 θ \theta θ 以使 J ( θ ) J(\theta) J(θ)变小,直到我们收敛到最小的 J ( θ ) J(\theta) J(θ),并得出 θ \theta θ的值。 这种算法又叫梯度下降算法(gradient descent)
对于梯度下降来讲,最重要的是每次下降多少,多久可以找到最优解(此处的最优解代表 J ( θ ) J(\theta) J(θ)已经到达最小)
θ j : = θ j − α 1 m ( ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j i ) (6) \theta_j:=\theta_j-\alpha\frac{1}{m}(\sum_{i=1}^{m}{(h_\theta(x^{(i)})-y^{(i)})}x_j^i)\tag{6} θj:=θj−αm1(i=1∑m(hθ(x(i))−y(i))xji)(6)
其中式中 i i i 代表某个样本的编号, j j j 代表某个特征编号。 α \alpha α叫做学习速率,学习速率的值就决定着梯度下降的步长有多大,值得注意的是,步长太小可能会导致数据无法收敛,而步长太大会导致直接跨过最小误差点,导致误差会越来越大,这个如果读者不太理解,可以去找一些有图的博客,很容易理解。对于上式的第二个多项式,即 1 m ( ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j i ) \frac{1}{m}(\sum_{i=1}^{m}{(h_\theta(x^{(i)})-y^{(i)})}x_j^i) m1(∑i=1m(hθ(x(i))−y(i))xji) 是通过(5)式,也就是 J ( θ ) J(\theta) J(θ)对 θ j \theta_j θj 求偏导得到的。
对于 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j i \sum_{i=1}^{m}{(h_\theta(x^{(i)})-y^{(i)})}x_j^i ∑i=1m(hθ(x(i))−y(i))xji的理解:
我们可以将上式进行拆解,对于某一组数量为m个的样本,更新特征 θ j \theta_j θj,可以得到如下:
∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j i = ( h θ ( x ( 1 ) ) − y ( 1 ) ) x j 1 ) + ( h θ ( x ( 2 ) ) − y ( 2 ) ) x j 2 ) + ⋯ + ( h θ ( x ( m ) ) − y ( m ) ) x j m ) \sum_{i=1}^{m}{(h_\theta(x^{(i)})-y^{(i)})}x_j^i=(h_\theta(x^{(1)})-y^{(1)})x_j^1)+(h_\theta(x^{(2)})-y^{(2)})x_j^2)+\cdots+(h_\theta(x^{(m)})-y^{(m)})x_j^m) i=1∑m(hθ(x(i))−y(i))xji=(hθ(x(1))−y(1))xj1)+(hθ(x(2))−y(2))xj2)+⋯+(hθ(x(m))−y(m))xjm)
我们应该可以很简单的看出,这个式子其实是两个向量相乘得到的,其中特殊的,当 i = 1 i=1 i=1时, ( h θ ( x ( 1 ) ) − y ( 1 ) ) (h_\theta(x^{(1)})-y^{(1)}) (hθ(x(1))−y(1)) 得出的是一个数值,我们设为 k 1 k_1 k1 ,对于一组m的样本我们应该得到一个向量,我们设为 e r r o r A r r a y errorArray errorArray:
e r r o r A r r a y = ( h θ ( x ( i ) ) − y ( i ) ) = [ k 1 k 2 ⋮ k m ] errorArray=(h_\theta(x^{(i)})-y^{(i)})=\left[ \begin{matrix} k_1 \\ k_2 \\ \vdots \\ k_m \end{matrix} \right] errorArray=(hθ(x(i))−y(i))=⎣ ⎡k1k2⋮km⎦ ⎤
对于 x j i x_j^i xji,我们记作 X j i X_j^i Xji(再提醒注意: i i i代表样本编号,一共m个样本, j j j代表某个样本中特征的编号,一共(j+1)个特征)则可得出:
X j i = [ 1 x 1 1 x 2 1 ⋯ x j 1 1 x 1 2 x 2 2 ⋯ x j 2 ⋮ ⋮ ⋯ ⋯ ⋮ 1 x 1 m x 2 m ⋯ x j m ] X_j^i=\left[ \begin{matrix} 1 & x_1^1 & x_2^1 & \cdots & x_j^1 \\ 1 &x_1^2 & x_2^2 & \cdots & x_j^2\\ \vdots & \vdots & \cdots & \cdots & \vdots\\ 1 &x_1^m & x_2^m & \cdots & x_j^m \end{matrix} \right] Xji=⎣ ⎡11⋮1x11x12⋮x1mx21x22⋯x2m⋯⋯⋯⋯xj1xj2⋮xjm⎦ ⎤
注意:我们假定 x 0 = 1 x_0=1 x0=1,则此时对于 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j i \sum_{i=1}^{m}{(h_\theta(x^{(i)})-y^{(i)})}x_j^i ∑i=1m(hθ(x(i))−y(i))xji我们可以换成标量表示法:
θ j : = θ j − α 1 m ( X j i T ∗ e r r o r A r r a y ) (7) \theta_j:=\theta_j-\alpha\frac{1}{m}({X_j^{i}}^{T}*errorArray)\tag{7} θj:=θj−αm1(XjiT∗errorArray)(7)
则对于上式,我们可以一次性更新所有的 θ \theta θ ,如果上式看不懂请多看几次,只要你有线代基础,这个是不难的。(7)式是基于(6)式转化而来的。
另外: 我们也可以使用正规方程来完成梯度下降,但是正规方程会出现不可逆的情况,当我们加上正则化防过拟合后,会解决这个不可逆的现象,此时用正规方程更方便,下面给出不加正则化的正规方程:
θ = ( X T X ) − 1 X T y (8) \theta=(X^TX)^{-1}X^Ty\tag{8} θ=(XTX)−1XTy(8)
上式使用 y = θ X y=\theta X y=θX推导出来的,读者如有兴趣可自行尝试推导,过程较简单就不赘述,此时(8)式出现逆矩阵,则可能会出现不可拟现象,虽有一定解决方式,算出来的答案很相近,但是会影响最后的精度。
最后我们看一下线性回归的拟合与优化图,该图来源在我的机器学习系列中线性回归二的案例中的图:机器学习入门之线性回归(2)- 多特征(python实现)
下图时是 J ( θ ) J(\theta) J(θ)的优化过程: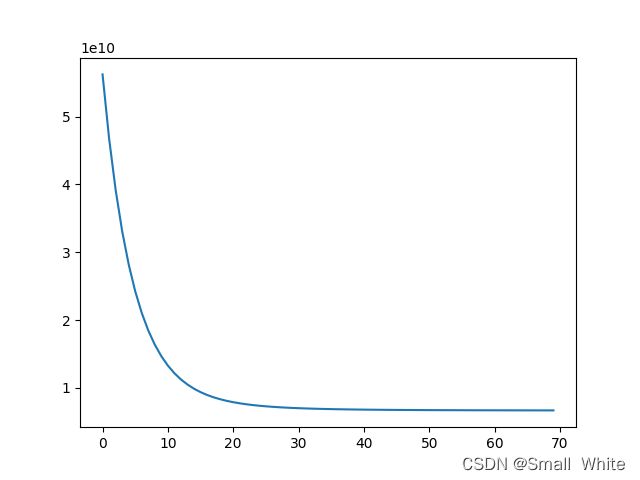
下图是最后线性回归拟合的模型:
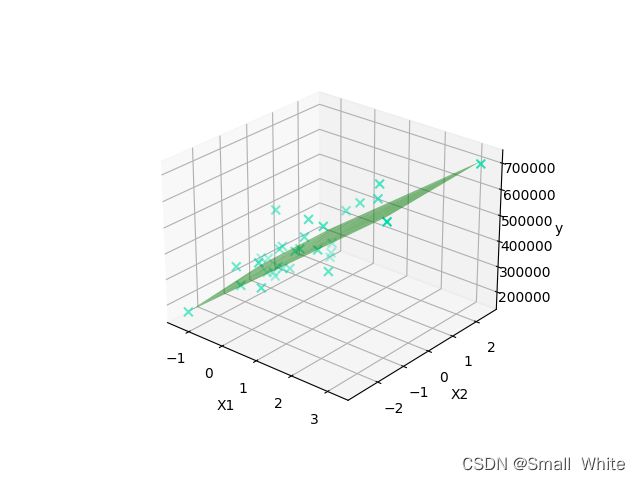
2. 逻辑回归
什么式逻辑回归?
根据维基百科的定义,逻辑回归用于分类,并对每个类别的概率进行建模。
举个例子:
假设现在有一个需要二分类的样本(所谓二分类就是只有两种分类结果,类似于true和false),样本是来预测一个人是否能考上大学。我们对于一个人能否考上大学可以有以下三个因素:总成绩( x 1 x_1 x1)、选修等级( x 2 x_2 x2)、身体素质检查( x 3 x_3 x3),那么我们逻辑所做的事情就是根据这些特征来判断某个人考上大学的概率是多少。注意:模型输出的并不是简单的是或否,而是概率。具体的是或否是根据你设置的阈值来决定的,例如当模型输出的概率大于50%时,我们就判定为可以上大学。
训练线性回归模型需要的几个组成部分:
① 假设函数
对于logistic回归,假设函数是sigmoid函数,形式如下:
h θ ( x ) = 1 1 + e − θ T x (9) h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}\tag{9} hθ(x)=1+e−θTx1(9)
其中 θ T x \theta^Tx θTx是与线性回归的目标函数是一样的,这里的sigmoid函数是通过logistic分布得来的,logistic分布函数:
F ( x ) = P ( X ≤ x ) = 1 1 + e − ( x − μ ) γ (10) F(x) = P(X≤x) = \frac{1}{1+e^{-\frac{(x-\mu)}{\gamma}}}\tag{10} F(x)=P(X≤x)=1+e−γ(x−μ)1(10)
可得到密度函数:
f ( x ) = e − ( x − μ ) γ γ ( 1 + e − ( x − μ ) γ ) 2 (11) f(x)=\frac{e^{-\frac{(x-\mu)}{\gamma}}}{\gamma(1+e^{-\frac{(x-\mu)}{\gamma}})^2}\tag{11} f(x)=γ(1+e−γ(x−μ))2e−γ(x−μ)(11)
其中上式中的 μ \mu μ和 γ \gamma γ分别是位置参数和形状参数
可以得到分布函数与概率密度的图像:
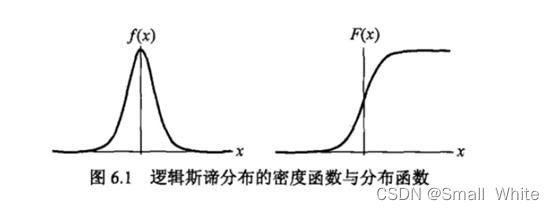
我们在分布函数,即函数(10)中的 μ \mu μ取值为0, γ \gamma γ取值为1,我们即可以得到sigmoid函数:
g ( z ) = 1 1 + e − z (12) g(z) = \frac{1}{1+e^{-z}}\tag{12} g(z)=1+e−z1(12)
其中
z = θ T x z = \theta^Tx z=θTx
这样就得到了(9)式,则我们可以sigmoid函数图像:
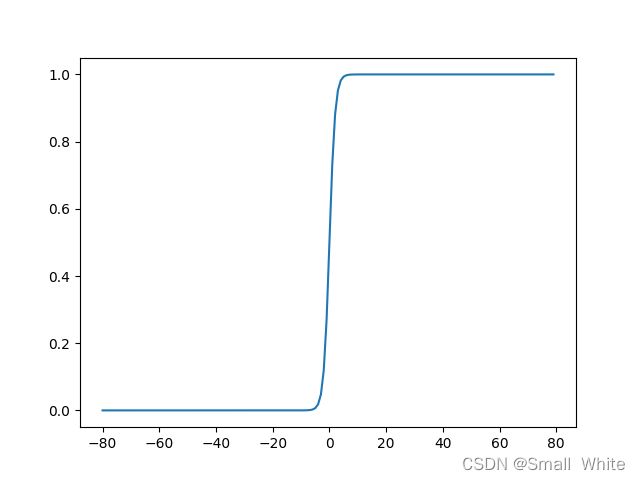
从(12)式和上面的图像中我们可以得知:
当 z → ∞ z\rightarrow\infty z→∞时, g ( z ) → 1 g(z)\rightarrow1 g(z)→1
当 z → − ∞ z\rightarrow-\infty z→−∞时, g ( z ) → 0 g(z)\rightarrow0 g(z)→0
当 z = 0 z=0 z=0时, g ( z ) = 0.5 g(z)=0.5 g(z)=0.5
这样我们可以假设设置阈值【当然阈值可以自己自由选择】,当 z > 0 z>0 z>0时,此时 g ( z ) > 0.5 g(z)>0.5 g(z)>0.5,则可以认为此时为1的概率值为100%,当 z ≤ 0 z≤0 z≤0时,此时 g ( z ) ≤ 0.5 g(z)≤0.5 g(z)≤0.5,则可以认为此时为0的概率值为100%
注意:对于输出的值我们可以认为是 p ( y = 1 ∣ x ; θ ) p(y=1|x;\theta) p(y=1∣x;θ)或 p ( y = 0 ∣ x ; θ ) p(y=0|x;\theta) p(y=0∣x;θ)
② 损失函数
对于损失函数,不能使用预测值与真实值差的平方的均值来实现,对于(9)式的目标函数,平方后是非凸函数(非凸函数是会有很多极小值,那么我们在梯度下降的时候是不容易找到最小值的),于是我们使用下列损失函数:
J ( θ ) = { − l n ( h θ ( x ) ) i f y = 1 − l n ( 1 − h θ ( x ) ) i f y = 0 (13) J(\theta) = \begin{cases} -ln(h_\theta(x)) & if \ y = 1\\ -ln(1-h_\theta(x)) & if \ y = 0 \end{cases}\tag{13} J(θ)={−ln(hθ(x))−ln(1−hθ(x))if y=1if y=0(13)
我们先分析 y = 1 y=1 y=1时的情况,为了方便理解,我们可以得到 − l n ( h θ ( x ) ) -ln(h_\theta(x)) −ln(hθ(x))的图像:
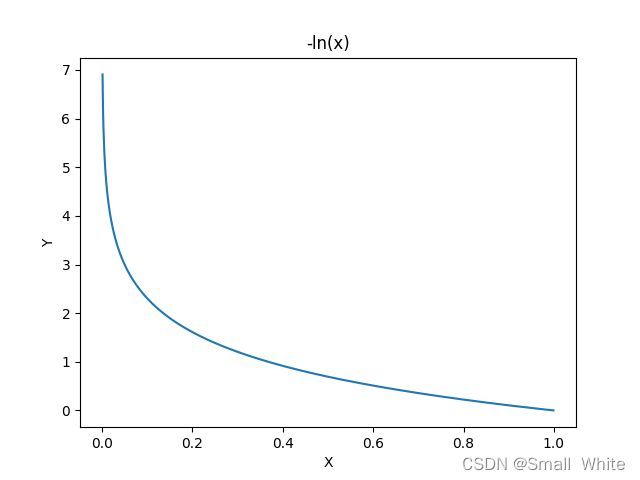
根据 y = 1 y=1 y=1时的 J ( θ ) J(\theta) J(θ)图像, y = 1 y=1 y=1时的损失函数这样理解:当 y = 1 y=1 y=1时,如果此时的 h θ ( x ) → 1 h_\theta(x)\rightarrow1 hθ(x)→1,我们可以知道此时预测值是正确的,那么此时的 J ( θ ) = − l n ( h θ ( x ) ) J(\theta)=-ln(h_\theta(x)) J(θ)=−ln(hθ(x))的值就趋向于0。如果此时 h θ ( x ) → 0 h_\theta(x)\rightarrow0 hθ(x)→0,此时的预测值是错误的,那么此时的误差就趋向于无穷(由于 − l n ( x ) -ln(x) −ln(x)在 x → 0 x\rightarrow0 x→0时,值是无穷大的),此时我们给模型一个非常大的惩罚项,来逼迫模型修改参数来进行拟合。
接下来分析 y = 0 y=0 y=0是的情况,为了方便理解,我们可以得到 − l n ( 1 − h θ ( x ) ) -ln(1-h_\theta(x)) −ln(1−hθ(x))的图像:
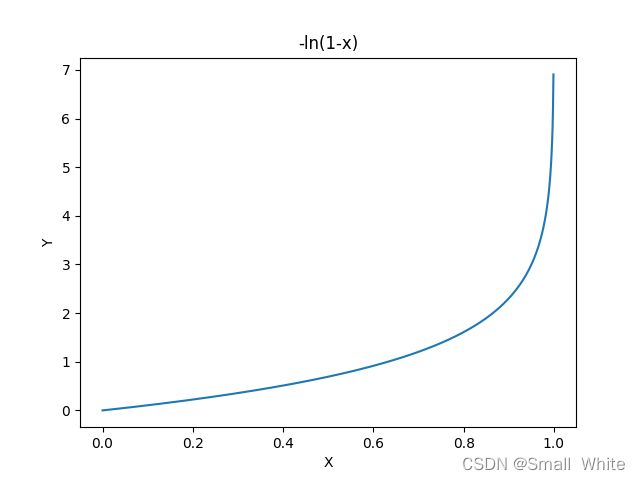
同样的,根据当 y = 0 y=0 y=0时的 J ( θ ) J(\theta) J(θ)图像, y = 0 y=0 y=0时的损失函数这样理解:当 y = 0 y=0 y=0时,如果此时的 h θ ( x ) → 0 h_\theta(x)\rightarrow0 hθ(x)→0,我们可以知道此时预测值是正确的,那么此时的 J ( θ ) = − l n ( 1 − h θ ( x ) ) J(\theta)=-ln(1-h_\theta(x)) J(θ)=−ln(1−hθ(x))的值就趋向于0。如果此时 h θ ( x ) → 1 h_\theta(x)\rightarrow1 hθ(x)→1,此时的预测值是错误的,那么此时的误差就趋向于无穷(由于 − l n ( 1 − x ) -ln(1-x) −ln(1−x)在 x → 1 x\rightarrow1 x→1时,值是无穷大的),此时我们给模型一个非常大的惩罚项,来逼迫模型修改参数来进行拟合。
注意:上述的分段函数再结合批量处理,我们可以合成一个下列损失函数:
J ( θ ) = 1 m ( ∑ i = 1 m ( − y ( i ) l n ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) l n ( 1 − h θ ( x ( i ) ) ) ) (14) J(\theta) = \frac{1}{m}(\sum_{i=1}^{m}(-y^{(i)}ln(h_\theta(x^{(i)}))-(1-y^{(i)})ln(1-h_\theta(x^{(i)})))\tag{14} J(θ)=m1(i=1∑m(−y(i)ln(hθ(x(i)))−(1−y(i))ln(1−hθ(x(i))))(14)
-
梯度下降
通过上面线性回归介绍,线性回归的 θ \theta θ更新减去的值(梯度值)是对 J ( θ ) J(\theta) J(θ)求偏导的来的,下面是求导过程:
先求 ( l n ( h θ ( x ) ) ′ (ln(h_\theta(x))' (ln(hθ(x))′
( l n ( h θ ( x ) ) ′ = l n ( 1 1 + e − θ x ) ′ = 1 h θ ( x ) ( − e − θ x ( 1 + e − θ x ) 2 ) x = − h θ ( x ) e − θ x x = − h θ ( x ) ( 1 + e − θ x − 1 ) x = − h θ ( x ) ( 1 h θ ( x ) − 1 ) x = ( h θ ( x ) − h θ ( x ) 1 h θ ( x ) ) x = − ( 1 − h θ ( x ) ) x (ln(h_\theta(x))' = ln(\frac{1}{1+e^{-\theta x}})'\\=\frac{1}{h_\theta(x)}(-\frac{e^{-\theta x}}{(1+e^{-\theta x})^2})x \\ = - h_\theta(x)e^{-\theta x }x \\ = - h_\theta(x)(1+e^{-\theta x }-1)x \\ = - h_\theta(x)(\frac{1}{h_\theta(x)}-1)x \\ =( h_\theta(x)-h_\theta(x)\frac{1}{h_\theta(x)})x \\=-(1-h_\theta(x))x (ln(hθ(x))′=ln(1+e−θx1)′=hθ(x)1(−(1+e−θx)2e−θx)x=−hθ(x)e−θxx=−hθ(x)(1+e−θx−1)x=−hθ(x)(hθ(x)1−1)x=(hθ(x)−hθ(x)hθ(x)1)x=−(1−hθ(x))x
同样的再求 ( l n ( 1 − h θ ( x ) ) ′ (ln(1-h_\theta(x))' (ln(1−hθ(x))′
( l n ( 1 − h θ ( x ) ) ′ = 1 1 − h θ ( x ) ( e − θ x ( 1 + e − θ x ) 2 ) x = 1 1 − h θ ( x ) ( 1 + e − θ x − 1 ( 1 + e − θ x ) 2 ) x = 1 1 − h θ ( x ) ( h θ ( x ) − h θ 2 ( x ) ) x = 1 1 − h θ ( x ) h θ ( x ) ( 1 − h θ ( x ) ) x = h θ ( x ) x (ln(1-h_\theta(x))' = \frac{1}{1-h_\theta(x)}(\frac{e^{-\theta x}}{(1+e^{-\theta x})^2})x \\ = \frac{1}{1-h_\theta(x)}(\frac{1+e^{-\theta x}-1}{(1+e^{-\theta x})^2})x \\ = \frac{1}{1-h_\theta(x)}(h_\theta(x)-h^2_\theta(x))x \\ = \frac{1}{1-h_\theta(x)}h_\theta(x)(1-h_\theta(x))x \\ = h_\theta(x)x (ln(1−hθ(x))′=1−hθ(x)1((1+e−θx)2e−θx)x=1−hθ(x)1((1+e−θx)21+e−θx−1)x=1−hθ(x)1(hθ(x)−hθ2(x))x=1−hθ(x)1hθ(x)(1−hθ(x))x=hθ(x)x
接下来我们可以对 J ( θ ) J(\theta) J(θ)求导:
J ′ ( θ ) = − 1 m ( ∑ i = 1 m ( − y ( i ) ( − ( 1 − h θ ( x ( i ) ) ) x j ( i ) ) − ( 1 − y ( i ) ) h θ ( x ( i ) ) x j ( i ) ) = − 1 m ( ∑ i = 1 m ( y ( i ) x ( i ) − y ( i ) h θ ( x ( i ) ) x j ( i ) ) − ( h θ ( x ( i ) ) x ( i ) − y ( i ) h θ ( x ( i ) ) x j ( i ) ) = − 1 m ( ∑ i = 1 m ( y ( i ) x ( i ) − h θ ( x ( i ) ) x j ( i ) ) ) = − 1 m ( ∑ i = 1 m ( y ( i ) − h θ ( x ( i ) ) ) x j ( i ) = 1 m ( ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) J'(\theta) = -\frac{1}{m}(\sum_{i = 1}^{m}(-y^{(i)}(-(1-h_\theta(x^{(i)}))x_j^{(i)})\\-(1-y^{(i)})h_\theta(x^{(i)})x_j^{(i)}) \\ = -\frac{1}{m}(\sum_{i = 1}^{m}(y^{(i)}x^{(i)}-y^{(i)}h_\theta(x^{(i)})x_j^{(i)})\\-(h_\theta(x^{(i)})x^{(i)}-y^{(i)}h_\theta(x^{(i)})x_j^{(i)}) \\ = -\frac{1}{m}(\sum_{i = 1}^{m}(y^{(i)}x^{(i)}-h_\theta(x^{(i)})x_j^{(i)})) \\ = -\frac{1}{m}(\sum_{i = 1}^{m}(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)} \\ = \frac{1}{m}(\sum_{i = 1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} J′(θ)=−m1(i=1∑m(−y(i)(−(1−hθ(x(i)))xj(i))−(1−y(i))hθ(x(i))xj(i))=−m1(i=1∑m(y(i)x(i)−y(i)hθ(x(i))xj(i))−(hθ(x(i))x(i)−y(i)hθ(x(i))xj(i))=−m1(i=1∑m(y(i)x(i)−hθ(x(i))xj(i)))=−m1(i=1∑m(y(i)−hθ(x(i)))xj(i)=m1(i=1∑m(hθ(x(i))−y(i))xj(i)
最后我们可以惊讶的得到的下降梯度与线性回归是相同的,此时对于逻辑回归梯度下降函数可以这样定义:
θ j : = θ j − α 1 m ( ∑ x = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ) (15) \theta_j := \theta_j - \alpha\frac{1}{m}(\sum_{x=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)})\tag{15} θj:=θj−αm1(x=1∑m(hθ(x(i))−y(i))xj(i))(15)
上面是关于逻辑回归的梯度下降的基本知识。 -
边界曲线
当我们指定 h θ ( x ) = 0.5 h_\theta(x) = 0.5 hθ(x)=0.5时作为阈值时,即 h θ ( x ) > 0.5 h_\theta(x) > 0.5 hθ(x)>0.5判定为1, h θ ( x ) ≤ 0.5 h_\theta(x) ≤ 0.5 hθ(x)≤0.5判定为0,从(1)式中我们可以得到当 z = θ T x = 0 z = \theta^T x = 0 z=θTx=0时,(1)式的值为0.5,即 h θ ( x ) = 0.5 h_\theta(x) = 0.5 hθ(x)=0.5,所以我们的边界曲线就是当 z = θ T x z = \theta^T x z=θTx为0时可得。例如: z = θ T x = θ 1 x 1 + θ 2 x 2 + θ 0 z = \theta^T x = \theta_1x_1+\theta_2x_2+\theta_0 z=θTx=θ1x1+θ2x2+θ0
此时的边界曲线是与 x 1 、 x 2 x_1、x_2 x1、x2相关的曲线: θ 1 x 1 + θ 2 x 2 + θ 0 = 0 \theta_1x_1+\theta_2x_2+\theta_0 = 0 θ1x1+θ2x2+θ0=0 -
高级优化方式
除了梯度下降时,我们有一些高级优化算法,可以自动帮助我们调整找合适的下降步长速率 α \alpha α,同时支持根据数据训练到损失函数最小,对于高级优化算法来讲,损失函数最小的评判标准是在进行训练时,损失函数有连续多次值不再下降。常见的高级优化算法有包括但不完全:
常见的优化方式 { 梯度下降 共轭梯度法 B F G S L − B F G C ⋯ 常见的优化方式\begin{cases} 梯度下降 \\ 共轭梯度法 \\ BFGS \\ L-BFGC \\ \cdots \end{cases} 常见的优化方式⎩ ⎨ ⎧梯度下降共轭梯度法BFGSL−BFGC⋯
由于逻辑回归的 α \alpha α与下降训练次数比较难确定,很难通过调整参数达到最优化,所以为了方便我们可以尽量采用高级优化方法。
我们最后看下逻辑回归的拟合与优化图,该图来源在我的机器学习系列中逻辑回归一的案例中的图:机器学习入门之逻辑回归(1)- 成绩预测是否进入大学(python实现)
下图时是 J ( θ ) J(\theta) J(θ)的优化过程:
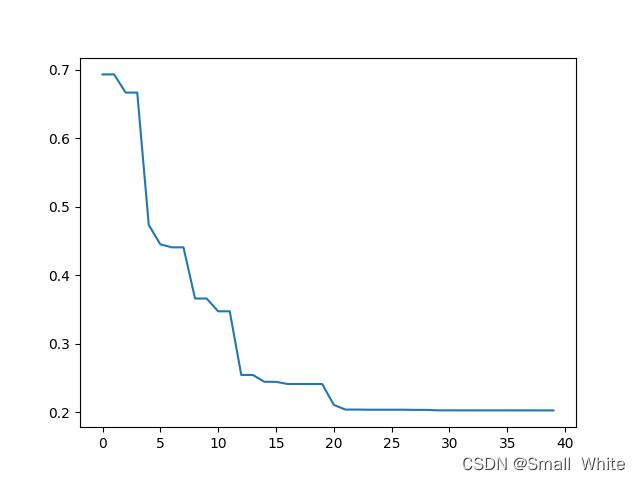
下图是最后逻辑回归拟合出的边界曲线:

最后是在测试集中的测试的准确率为90%:

三、人工神经网络基础
1. 从逻辑回归到神经网络
我们什么时候不选择逻辑回归而选择神经网络做分类呢,神经网络相比逻辑回归有什么优势呢?往下看看吧!
在上面聊的逻辑回归中,其实还有一种边界曲线并不是线性的,我们一般称之为非线性的逻辑回归。顾名思义,非线性就是我们最后拟合出来的决策边界并不是线性的,大部分可能是不规则的边界。例如,在我的机器学习系列中逻辑回归二的案例中的图:机器学习入门之逻辑回归(2)- 微芯片质量预测-非线性(python实现)
下面是拟合后的边界曲线:

优化图像:

正确率:
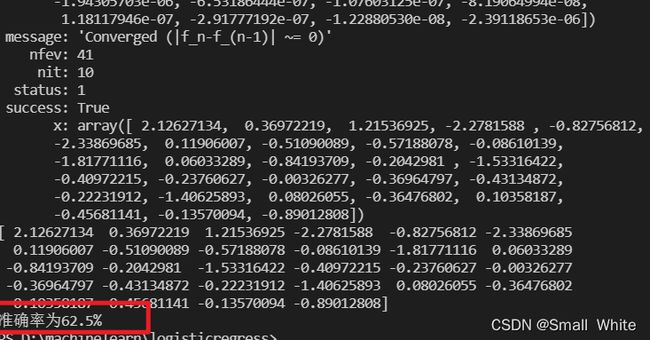
如果你不太了解怎么用低维的特征来拟合出一个非线性的边界,那么我建议你可以去尝试去理解和完成一下我的那一篇博客的代码
如何用低维的数据拟合出非线性边界?
在这我们简单来说:假设一个样本中只有两个特征 x 1 、 x 2 x_1、x_2 x1、x2, 如果我们只用两个特征去拟合它,只会得到一个线性的分界线,在上文中逻辑回归部分的案例图中是两个特征拟合出来的边界。如果我们需要拟合出来一个非线性的曲线,那么就需要升维,也就是将只有 x 1 、 x 2 x_1、x_2 x1、x2的项升维到 x 1 , x 2 , x 1 2 , x 1 x 2 , x 2 2 , ⋯ , x 2 n x_1,x_2,x_1^2,x_1x_2,x_2^2,\cdots,x_2^n x1,x2,x12,x1x2,x22,⋯,x2n,以增强特征对方程的影响(下文会写这样升维的原因,此处先了解一下这样升维能得到非线性边界即可)。本篇案例中升维到了 x i 6 x_i^6 xi6,升维后就到了28个特征,此时我们会得到非线性的边界,但是,为了消除高阶对拟合的影响,即防止出现过拟合线性,我们要对其损失函数进行正则化。
正则化:指在损失函数中加上惩罚项,让高阶的特征(高阶的特征指假设函数对应的特征变量的指数太大的项,例如 θ 1 x 1 10 + θ 2 x 2 + θ 0 \theta_1x_1^{10}+\theta_2x_2+\theta_0 θ1x110+θ2x2+θ0,此时显然特征 x 1 x_1 x1的阶数较高,我们就尽量减少 θ 1 的数值 \theta_1的数值 θ1的数值,让 x 1 x_1 x1对整个函数的影响变小)对应的系数 θ j \theta_j θj变得非常小,这样就会减少高阶特征对函数的影响,从而降低了量级,使维度减少,但是并没有裁剪任何特征,表明任何特征都对方程拟合还是有影响的)
逻辑回归做非线性边界的弊端?
上述仅仅只有两个特征,我们为了拟合出比较完美的边界已经将特征升到了 x 2 6 x_2^6 x26,也就是达到了28个特征,即28维。试想,假如我们初始有100个特征,要做非线性的边界,当升维后我们会得到以下函数:
g ( x 1 2 , x 1 x 2 , x 1 x 3 , x 1 x 4 , ⋯ , x 1 x 100 , x 2 2 , x 1 x 3 , ⋯ ) g(x_1^2,x_1x_2,x_1x_3,x_1x_4,\cdots,x_1x_{100},x_2^2,x_1x_3,\cdots) g(x12,x1x2,x1x3,x1x4,⋯,x1x100,x22,x1x3,⋯)
由此我们得出逻辑回归的弊端一:我们可以看到升维后的特征大约有3000多个,若是加上三个特征的复合项 x i × x j × x k x_i×x_j×x_k xi×xj×xk会更多。升维后的特征数量太多,项数太多,那么最后的结果可能是过拟合的,也会导致计算量太大,显然这是不合适的。
有的读者到这可能会有疑问既然升维会有这些问题,我们为什么要升维呢?
假如我们有三个特征 x 1 、 x 2 x_1、x_2 x1、x2,若是不升维,此时得到的一定是一个线性边界。
h θ ( x ) = θ 1 x 1 + θ 2 x 2 + θ 0 h_\theta(x) = \theta_1x_1+\theta_2x_2+\theta_0 hθ(x)=θ1x1+θ2x2+θ0
若是只升维至平方项,而没有复合项,我们可能得到的只是圆或者椭圆等图像:
h θ ( x ) = θ 1 x 1 + θ 2 x 2 + θ 3 x 1 2 + θ 4 x 2 2 + θ 0 h_\theta(x) = \theta_1x_1+\theta_2x_2+\theta_3x_1^2+\theta_4x_2^2+\theta_0 hθ(x)=θ1x1+θ2x2+θ3x12+θ4x22+θ0
所以当我们加上复合项时才能拟合出更复杂的边界(本例中复合项是例如 x 1 × x 2 的形式 x_1×x_2的形式 x1×x2的形式)。
我们选举更能说明问题的例子:样本为图片时
假设有一张灰色图片(所谓灰色图片就是不包含RGB三原色的图片),它的大小为50×50像素(这样的分辨率很不高,图像模糊),则一共2500个像素:
X = [ 像素块 1 ( 0 − 255 ) 像素块 2 ( 0 − 255 ) ⋮ 像素块 2500 ( 0 − 255 ) ] X =\left[ \begin{matrix} 像素块1(0-255) \\ 像素块2(0-255)\\ \vdots \\ 像素块2500(0-255) \end{matrix} \right] X=⎣ ⎡像素块1(0−255)像素块2(0−255)⋮像素块2500(0−255)⎦ ⎤
那么针对上述矩阵仅仅关于两个特征的复合特征 x i × x j x_i×x_j xi×xj的数量就多达300万个,那么我们不难看出升维后的特征数量是非常庞大的,如果使用传统的logistic回归会导致过拟合和计算量太大等问题,此时考虑神经网络在非线性假设的应用是一种好的算法。
另外逻辑回归还有一个小的弊端二:就是使用逻辑回归表达多分类模型时,需要将多分类转化为多个二分类表示。例如:假设一个样本有三个分类结果输出,分别是分类一、分类二、分类三,此时我们要将该分类问题分化为三个二分类模型,它们分别是:
分解的三个模型 { 模型一(二分类,即只有两个结果):分类一概率和其它概率(其它包含分类二和分类三) 模型二(二分类,即只有两个结果):分类二概率和其它概率(其它包含分类一和分类三) 模型三(二分类,即只有两个结果):分类三概率和其它概率(其它包含分类一和分类二) 分解的三个模型\begin{cases} 模型一(二分类,即只有两个结果):分类一概率和其它概率(其它包含分类二和分类三) \\ 模型二(二分类,即只有两个结果):分类二概率和其它概率(其它包含分类一和分类三) \\ 模型三(二分类,即只有两个结果):分类三概率和其它概率(其它包含分类一和分类二) \\ \end{cases} 分解的三个模型⎩ ⎨ ⎧模型一(二分类,即只有两个结果):分类一概率和其它概率(其它包含分类二和分类三)模型二(二分类,即只有两个结果):分类二概率和其它概率(其它包含分类一和分类三)模型三(二分类,即只有两个结果):分类三概率和其它概率(其它包含分类一和分类二)
当使用第一个模型预测时,发现输出结果不是分类一而是其它时,则使用模型二继续预测,若不是分类二,然后模型三尝试,直到找到归属的分类,上面是逻辑回归面对多分类问题时的处理方法。那么,如果有没有一种方法,让结果输出一个向量可以一次性表示多分类的所有可能,这样我们只用训练一个模型就可以?
我们的人工神经网络是可以的,神经网络在描述多分类问题时,在输出层可以输出一个结果向量,例如上面那个例子,在输出层可以输出下列结果向量:
y = [ 0 1 0 ] y =\left[ \begin{matrix} 0 \\ 1\\ 0 \end{matrix} \right] y=⎣ ⎡010⎦ ⎤
代表的含义如下:
y = [ P ( 分类一 ) ≈ 0 P ( 分类二 ) ≈ 1 P ( 分类三 ) ≈ 0 ] y =\left[ \begin{matrix} P(分类一)\approx0 \\ P(分类二)\approx1\\ P(分类三)\approx0 \end{matrix} \right] y=⎣ ⎡P(分类一)≈0P(分类二)≈1P(分类三)≈0⎦ ⎤
那么我们可以得出该预测结果为分类二
当然选用神经网络的原因并非只有这些,有很多其它的因素促使我们去学习与使用该算法,在处理一些问题上会更加的简洁有效。
2. 神经元模型
什么是神经网络?
神经网络(维基):现代神经网络是一种非线性统计性数据建模工具,神经网络通常是通过一个基于数学统计学类型的学习方法(Learning Method)得以优化,所以也是数学统计学方法的一种实际应用。
由于人工神经网络的灵感来自于人类的神经系统,那么我们再来简单看一下人类神经系统的工作方式:
组成神经系统的神经元彼此以突起(树突和轴突)相互联系形成的联络网。又称神经回路或神经元回路。通过神经网络可以将来自体内外的各种感觉信息进行加工,并控制和调节机体的各种活动。
我们可以举一个抽象的例子,当我们的视觉捕捉到一个物体时,在我们的视觉中可能产生一组信号(可能会很复杂,我们不知道信号具体是什么样子的),首先这组信号会通过人体的神经系统处理,转化成我们的视觉处理的大脑皮层可以处理的信号,通过大脑皮层处理之后,会输出一个信号,告诉大脑这个物体是什么东西,做什么用的等一些信息。那么在我们接收物体信号到大脑皮层输出物体分类与信息的过程中,可能经历了很多的处理阶段,每个阶段都会对其信号进行加工。对比人工神经网络,它中间也包含了以下几个层:
输入层(接受样本数据,相当于眼睛接收物体信号)、隐藏层(处理与转化样本数据,相当于到达大脑皮层之前的神经系统的信号处理,注意:这个过程可能不只有一个阶段,可能经历了一系列阶段)、输出层(输出结果,相当于大脑皮层处理并输出了物体分类与信息)
下面是一个只包含输入层与输出层的神经元模型:
特征向量如下,其中 x 0 x_0 x0我们称作偏置单元,在方程中一般是常数项,用来调节方程,相当于得到线性回归方程中的常数项 θ 0 \theta_0 θ0,只不过此处的 x 0 x_0 x0不再恒为1:
X = [ x 0 x 1 x 2 x 3 ] (16) X = \left[ \begin{matrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{matrix} \right]\tag{16} X=⎣ ⎡x0x1x2x3⎦ ⎤(16)
参数(也可叫权重)如下:
Θ = [ θ 0 θ 1 θ 2 θ 3 ] (17) \Theta = \left[ \begin{matrix} \theta_0 \\ \theta_1 \\ \theta_2 \\ \theta_3 \end{matrix} \right]\tag{17} Θ=⎣ ⎡θ0θ1θ2θ3⎦ ⎤(17)
网络结构如下:
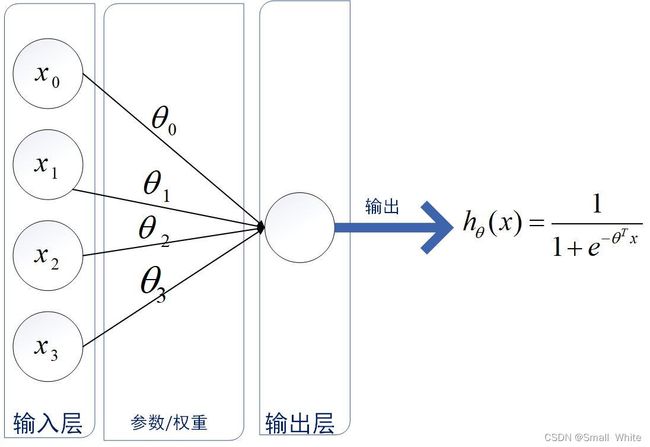
我们在这解释一下上面的图各个部分的含义:
最左侧是网络的输入层,它是用来接收样本中的对应的特征值。
每条从输入层到输出层的路线上都会有权重 θ \theta θ,这个 θ \theta θ 的作用与我们在线性回归 与逻辑回归的作用相同,是作为优化参数出现的,通过调节 θ \theta θ的值,使得损失函数达到最小。
输出层包含一个 h θ ( x ) h_\theta(x) hθ(x),了解逻辑回归的读者应该很熟悉这个公式,这是逻辑回归的常用的目标函数sigmoid函数,通过特征与对应权重相乘后相加,传入到sigmoid函数得出输出结果,这个等价于我们做了一个逻辑回归模型。
上述网络结构我们也可称为单层感知机
在上面的网络结构中,最后输出层的 h θ ( x ) h_\theta(x) hθ(x),在神经网络中,我们有专有的名词,叫做激活函数
为了能帮助读者理解神经网络结构与激励函数,我们下面看一个更加复杂神经网络结构(此例中使用的特征向量与权重向量还是式(15)和式(16)向量):
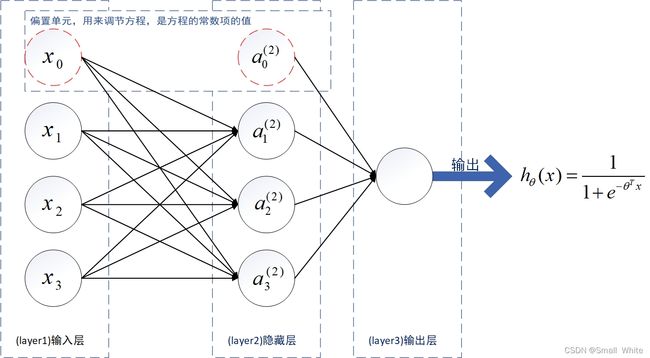
说明一下命名规则(如果记不住可以多回来看看呦):
① 本文中,用 L / l L/l L/l 表示层数,例如 a ( l ) a^{(l)} a(l)表示第 l l l 层网络, a ( 1 ) a^{(1)} a(1)表示第1层网络,即输入层。
② 本文中,用 a i ( l ) a_i^{(l)} ai(l)表示第 l l l 层的第 i i i个神经单元激活项,所谓激活项代表由一个神经元计算并输出的值
③ 本文中,用 θ j i ( l ) \theta_{ji}^{(l)} θji(l)表示从第 l l l 层的第 i i i 个神经元到第 l + 1 l+1 l+1 层的第 j j j 个单元的权重。例如 θ 10 ( 1 ) \theta_{10}^{(1)} θ10(1)代表从第一层(输入层)的第0个神经元,即 x 0 x_0 x0到第二层(隐藏层)的第1个单元,即 a 1 ( 2 ) a_1^{(2)} a1(2)的权重。这样表示可能不太符合我们的常规理解方式,但是如果将所有的 θ \theta θ 形成一个矩阵的时候,会很方便计算出下一层的任意单元的值。
为了方便理解,我们将第一层到第二层的所有的 θ \theta θ 表示成一个矩阵
Θ ( 1 ) = [ θ 10 ( 1 ) θ 11 ( 1 ) θ 12 ( 1 ) θ 13 ( 1 ) θ 20 ( 1 ) θ 21 ( 1 ) θ 22 ( 1 ) θ 23 ( 1 ) θ 30 ( 1 ) θ 31 ( 1 ) θ 32 ( 1 ) θ 33 ( 1 ) ] \Theta^{(1)} = \left[ \begin{matrix} \theta_{10}^{(1)} & \theta_{11}^{(1)} & \theta_{12}^{(1)} & \theta_{13}^{(1)} \\ \theta_{20}^{(1)} & \theta_{21}^{(1)} & \theta_{22}^{(1)} & \theta_{23}^{(1)} \\ \theta_{30}^{(1)} & \theta_{31}^{(1)} & \theta_{32}^{(1)} & \theta_{33}^{(1)} \end{matrix} \right] Θ(1)=⎣ ⎡θ10(1)θ20(1)θ30(1)θ11(1)θ21(1)θ31(1)θ12(1)θ22(1)θ32(1)θ13(1)θ23(1)θ33(1)⎦ ⎤
则利用上述矩阵的第一行,我们可以求出 a 1 ( 2 ) a_1^{(2)} a1(2)
则利用上述矩阵的第二行,我们可以求出 a 2 ( 2 ) a_2^{(2)} a2(2)
…
当然,我们如果用 θ i j ( l ) \theta_{ij}^{(l)} θij(l)来表示,利用转置也可以正常计算的,只不过增加了一部分转置的计算量。
④ 本文中,用 z i ( l ) z_i^{(l)} zi(l)表示计算第 l l l 层的第 i i i个神经单元通过 Θ T X \Theta^TX ΘTX得到的值,例如
z 1 ( 2 ) = θ 10 ( 1 ) x 0 + θ 11 ( 1 ) x 1 + θ 12 ( 1 ) x 2 + θ 13 ( 1 ) x 3 z_1^{(2)} = \theta_{10}^{(1)}x_0+\theta_{11}^{(1)}x_1 +\theta_{12}^{(1)}x_2 +\theta_{13}^{(1)}x_3 z1(2)=θ10(1)x0+θ11(1)x1+θ12(1)x2+θ13(1)x3
⑤ 本文中,默认的激活函数是sigmoid函数,用 g ( z ) g(z) g(z)表示,其余常见的激活函数还有Softmax、Tanh、Relu等,此处我们不讨论激活函数,有疑问的读者可自行了解。
总而言之:
l l l 代表层数,位于参数上标
j j j 代表 l + 1 l+1 l+1 层(即下一层)的第 j j j 个神经单元,位于参数下标
i i i 代表第 l l l 层(即当前层)的第 i i i 个神经单元,位于参数下标
本文所有出现的激活函数 g ( z ) g(z) g(z)均是sigmoid函数
此神经网络具有三层结构,输入层与输出层我们在上一个例子中已经聊过了,来看一下隐藏层。
隐藏层:隐藏层代表中间的计算过程(想当于人的神经系统的信息加工),无法看到,隐藏层有可能不只是一个,一般情况下每个隐藏层中的每个神经单元都需要用激活函数做非线性变换计算并需要将计算出的值(即激活项)当作初始值参与计算下一层神经单元的激活项。
一个有规律的点:如果网络在第 l l l 层有 s l s_l sl 个单元,在 l + 1 l+1 l+1 层有 s l + 1 s_{l+1} sl+1 个单元,则 Θ ( l ) \Theta^{(l)} Θ(l)的维度为 ( s l + 1 ) ∗ s l + 1 (s_l+1)*s_{l+1} (sl+1)∗sl+1.其中 s l + 1 s_l+1 sl+1中加的1是第 l l l 层的偏置项
如何理解上面的规律呢?我们看上面三层网络的例子,比如我们求第一层(也就是输入层)到第二层(也就是隐藏层)的 Θ ( 1 ) \Theta^{(1)} Θ(1)的维度(其实上面已经求过了,是12个),我们看第一层参与计算的单元数量的3个(我们现在不加偏置项 x 0 x_0 x0,在计算时使用 ( s 1 + 1 ) (s_1+1) (s1+1) 即可),分别是 x 1 至 x 3 x_1至x_3 x1至x3,第二层参与计算的是3个,分别是 a 1 ( 2 ) 至 a 3 ( 2 ) a_1^{(2)}至a_3^{(2)} a1(2)至a3(2)(注意:由于 a 0 ( 2 ) a_0^{(2)} a0(2)是偏置项,只参与计算下一层的神经单元的值,并不参与计算本层的神经单元的值),故我们得到 ( s j + 1 ) ∗ s j + 1 = 4 ∗ 3 = 12 (s_j+1)*s_{j+1} = 4 *3 = 12 (sj+1)∗sj+1=4∗3=12
所以,对于上面的三层的神经网络,我们可以表示出所有隐藏层的所有激活项:
a 1 ( 2 ) = g ( z 1 ( 2 ) ) = g ( θ 10 ( 1 ) x 0 + θ 11 ( 1 ) x 1 + θ 12 ( 1 ) x 2 + θ 13 ( 1 ) x 3 ) a 2 ( 2 ) = g ( z 2 ( 2 ) ) = g ( θ 20 ( 1 ) x 0 + θ 21 ( 1 ) x 1 + θ 22 ( 1 ) x 2 + θ 23 ( 1 ) x 3 ) a 3 ( 2 ) = g ( z 3 ( 2 ) ) = g ( θ 30 ( 1 ) x 0 + θ 31 ( 1 ) x 1 + θ 32 ( 1 ) x 2 + θ 33 ( 1 ) x 3 ) a_1^{(2)} = g(z_1^{(2)} ) = g( \theta_{10}^{(1)}x_0+\theta_{11}^{(1)}x_1 +\theta_{12}^{(1)}x_2 +\theta_{13}^{(1)}x_3 ) \\ a_2^{(2)} = g(z_2^{(2)} ) = g( \theta_{20}^{(1)}x_0+\theta_{21}^{(1)}x_1 +\theta_{22}^{(1)}x_2 +\theta_{23}^{(1)}x_3 ) \\ a_3^{(2)} = g(z_3^{(2)} ) = g( \theta_{30}^{(1)}x_0+\theta_{31}^{(1)}x_1 +\theta_{32}^{(1)}x_2 +\theta_{33}^{(1)}x_3 ) a1(2)=g(z1(2))=g(θ10(1)x0+θ11(1)x1+θ12(1)x2+θ13(1)x3)a2(2)=g(z2(2))=g(θ20(1)x0+θ21(1)x1+θ22(1)x2+θ23(1)x3)a3(2)=g(z3(2))=g(θ30(1)x0+θ31(1)x1+θ32(1)x2+θ33(1)x3)
对于输出层我们可以计算出激活项:
h θ ( x ) = a 1 ( 3 ) = g ( θ 10 ( 2 ) x 0 + θ 11 ( 2 ) x 1 + θ 12 ( 2 ) x 2 + θ 13 ( 2 ) x 3 ) h_\theta(x) = a_1^{(3)} = g(\theta_{10}^{(2)}x_0+\theta_{11}^{(2)}x_1 +\theta_{12}^{(2)}x_2 +\theta_{13}^{(2)}x_3 ) hθ(x)=a1(3)=g(θ10(2)x0+θ11(2)x1+θ12(2)x2+θ13(2)x3)
希望上述公式可以帮助读者理解符号代表的含义和神经网络结构。
3. 从单层感知机到多层感知机
在继续往下学习神经网络之前,很有必要学习一下神经网络的更基础的知识—感知机
什么是感知机?
感知机由Rosenblatt在1957年提出,是一种二类线性分类模型。输入一个实数值的n维向量(特征向量),经过线性组合,如果结果大于某个数,则输出1,否则输出-1,具体地:
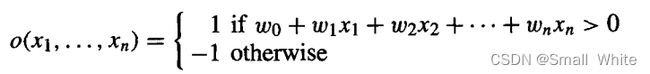
其中的 w 0 , w 1 , . . . . w n w_0,w_1,....w_n w0,w1,....wn权重, W W W向量称为权向量(本文中粗体代表向量)。权重决定每个输入分类对最终输出的贡献率。为了更简洁地表示,我们加入一个x0=1,则可以将上面的式子写成符号函数(输入大于零的时候为1,其他为-1):
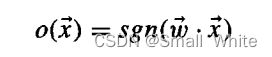
这就是感知机的数学表达,其中 W ∗ X W*X W∗X为内积,即向量对应元素相乘,然后求和。
感知机的几何解释:
可以把感知机看成 n n n维实例空间的决策超平面: W ∗ X = 0 W*X=0 W∗X=0.这个超平面将空间中的点分为正负两类。如果给定的杨莉集线性可分,则可以将每个样例准确地分为两类,称为分类超平面。而其中( w 1 , w 2 , ⋯ , w n w_1,w_2,\cdots,w_n w1,w2,⋯,wn)为这个超平面的法向量, w 0 w_0 w0称为截距。
布尔函数的感知机表示:
一个感知机单元可以用来表示许多(不是全部)布尔函数,为了读者能更好的理解布尔函数的感知机表示,以及为什么要从单层感知机到多层感知机,下面我们详细举例用单层或多层感知机实现AND、OR、非、XNOR(同或)
- AND(与)
对于与门读者应该不陌生吧,假如 x 1 A N D x 2 x_1 AND x_2 x1ANDx2,只有当 x 1 与 x 2 x_1与x_2 x1与x2都是1时,结果才是1,否则只要 x 1 、 x 2 x_1、x_2 x1、x2有0出现,结果就是0
我们可以画出与门的图像如下:

其中圆点代表结果为0,x代表结果为1,我们看到利用一条直线就可以区分0和1,那么利用逻辑回归做线性边界就可以表达出来,上文聊过,单层感知机就相当于另一种表达方式实现了逻辑回归,所以用单层感知机就可以表达出AND

再回顾一下sigmoid的图像:
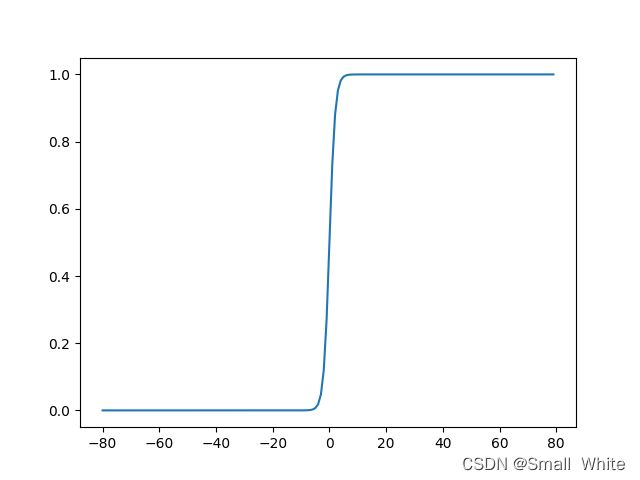
从上面的图像中可以得到 g ( − 5 ) ≈ 0 g(-5)\approx0 g(−5)≈0, g ( 5 ) ≈ 1 g(5)\approx1 g(5)≈1
我们可以得到 z 1 ( 2 ) z_1^{(2)} z1(2)(第二层的第一个单元,就是输出单元):
z 1 ( 2 ) = 10 x 1 + 1 0 2 − 15 z_1^{(2)} = 10x_1+10_2-15 z1(2)=10x1+102−15
将 x 1 、 x 2 x_1、x_2 x1、x2取值分别代入 z 1 ( 2 ) z_1^{(2)} z1(2),并将 z 1 ( 2 ) z_1^{(2)} z1(2)代入sigmoid函数,可得下表:
| x 1 x_1 x1 | x 2 x_2 x2 | z 1 ( 2 ) z_1^{(2)} z1(2) | g ( z 1 ( 2 ) ) g(z_1^{(2)}) g(z1(2)) | 输出 |
|---|---|---|---|---|
| 0 | 0 | -15 | ≈ 0 \approx0 ≈0 | 0 |
| 0 | 1 | -5 | ≈ 0 \approx0 ≈0 | 0 |
| 1 | 0 | -5 | ≈ 0 \approx0 ≈0 | 0 |
| 1 | 1 | 5 | ≈ 1 \approx1 ≈1 | 1 |
上面就利用单层感知机实现了AND与 操作,可以总结出,能实现与操作,偏置项是很很重要的,现在我们只需要改一下偏置项即可以得到或操作。
2. OR(或)
关于OR或操作,假如 x 1 O R x 2 x_1 OR x_2 x1ORx2,只有当 x 1 与 x 2 x_1与x_2 x1与x2都是0时,结果才是0,否则只要 x 1 、 x 2 x_1、x_2 x1、x2有1出现,结果就是1
我们可以得到或的图像:

上图中实心圆圈代表0,× 代表1
同样的,这个也是可以使用逻辑回归做线性拟合,拟合出线性的边界。使用单层感知机可以表达出来,如下图:
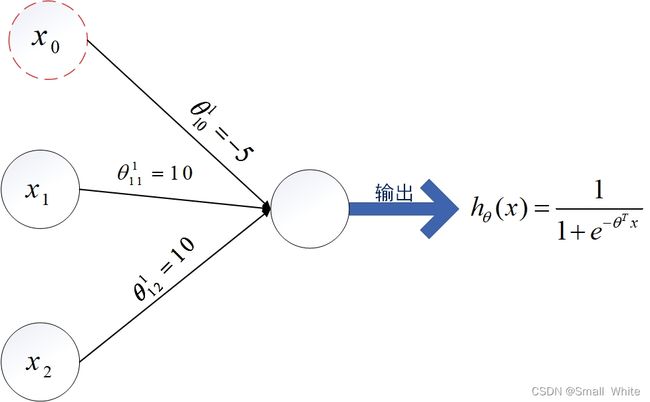
可以看到,和AND操作的感知机表示图相比,OR仅仅改变了 θ 10 ( 1 ) \theta_{10}^{(1)} θ10(1)的值,可以同样写出 z 1 ( 2 ) z_1^{(2)} z1(2)(第二层的第一个单元,就是输出单元):
z 1 ( 2 ) = 10 x 1 + 1 0 2 − 5 z_1^{(2)} = 10x_1+10_2-5 z1(2)=10x1+102−5
分别将 x 1 、 x 2 x_1、x_2 x1、x2代入,则我们可以得出下表:
| x 1 x_1 x1 | x 2 x_2 x2 | z 1 ( 2 ) z_1^{(2)} z1(2) | g ( z 1 ( 2 ) ) g(z_1^{(2)}) g(z1(2)) | 输出 |
|---|---|---|---|---|
| 0 | 0 | -5 | ≈ 0 \approx0 ≈0 | 0 |
| 0 | 1 | 5 | ≈ 1 \approx1 ≈1 | 1 |
| 1 | 0 | 5 | ≈ 1 \approx1 ≈1 | 1 |
| 1 | 1 | 15 | ≈ 1 \approx1 ≈1 | 1 |
上面我们仅仅改变了偏置项即可以得到了OR 或操作
3. 非
非运算就是对输入项取反的过程,例如 x 1 = 0 x_1 = 0 x1=0,取反后 x 1 = 1 x_1 = 1 x1=1,同样的 x 1 = 1 x_1 = 1 x1=1,取反后 x 1 = 0 x_1 = 0 x1=0。
此操作结果只有两个:0或者1,则一定可以找出一个直线(例如直线 x = 0.5 x=0.5 x=0.5)将结果分类。所以用单层感知机可以完成非操作
从上述表达可以得出,此感知机除偏置项外只有一个特征输入项,则可以得到下图:

可以同样写出 z 1 ( 2 ) z_1^{(2)} z1(2)(第二层的第一个单元,就是输出单元):
z 1 ( 2 ) = − 10 x 1 + 5 z_1^{(2)} = -10x_1+5 z1(2)=−10x1+5
分别将 x 1 、 x 2 x_1、x_2 x1、x2代入,则我们可以得出下表:
| x 1 x_1 x1 | z 1 ( 2 ) z_1^{(2)} z1(2) | g ( z 1 ( 2 ) ) g(z_1^{(2)}) g(z1(2)) | 输出 |
|---|---|---|---|
| 0 | 5 | ≈ 1 \approx1 ≈1 | 1 |
| 1 | -5 | ≈ 0 \approx0 ≈0 | 0 |
上面看到,利用单层感知机可以处理一些分类界限比较清晰规整,一般只能用线性表达出来的分类问题,那么如果是非线性的分类问题,怎么样才能用感知机表达出来呢?比如说一个简单的同或或者异或都无法表达。这也是前期一直困扰科学家的地方,下面看看为什么单层感知机无法表达同或。
4. XNOR(同或)
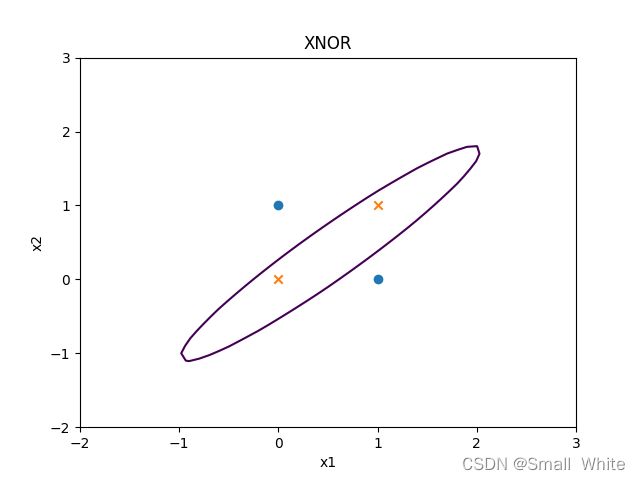
同或是只有 x 1 、 x 2 x_1、x_2 x1、x2的取值相同时,结果是1,取值不相同时,结果为0,我们可以得到同或可能的拟合图像:
上图拟合的曲线方程为: z = 12.799 x 1 2 − 25.410 x 1 x 2 + 13.811 x 2 2 − 4.55 x 1 + 3.68 x 2 − 2 z = 12.799x_1^2-25.410x_1x_2+13.811x_2^2-4.55x_1+3.68x_2-2 z=12.799x12−25.410x1x2+13.811x22−4.55x1+3.68x2−2 注意:拟合方程不唯一,这是上述图像的方程
其中上图中实心圆圈代表0,× 代表1
从上图中可以看出,我们不能再使用一条直线去将两种结果进行分类,需要用非线性的方式来表示。上面聊过,对于一个单层感知机,是没有办法表示非线性的方程的。所以我们需要因为多层感知机,由于多层感知机会利用激活函数进行非线性变换,从而得到非线性方程边界,实际上只用两层的感知机,我们就能表达出来同或或者异或 。下面是两层的感知机网络图:
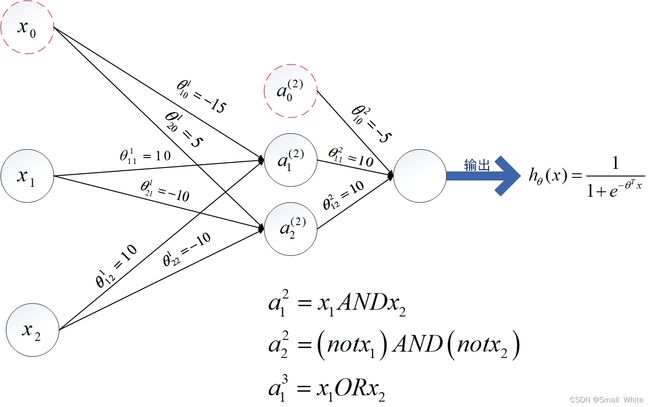
我们分析一下上图,首先在第二层能得到:
z 1 2 = 10 x 1 + 10 x 2 − 15 z 2 2 = − 10 x 1 − 10 x 2 + 5 z_1^2 = 10x_1+10x_2-15 \\ z_2^2 = -10x_1-10x_2+5 z12=10x1+10x2−15z22=−10x1−10x2+5
针对 z 1 2 z_1^2 z12,上面的AND已经聊过了,和AND是同一个方程。
那么 z 2 2 z_2^2 z22,我们将 x 1 、 x 2 x_1、x_2 x1、x2分别代入,发现它与AND的结果正好相反,那么就相当于对 x 1 、 x 2 x_1、x_2 x1、x2取反然后用AND(总体取反可以分配到各个特征取反)
我们可以得到 a 1 ( 2 ) a_1^{(2)} a1(2)和 a 2 ( 2 ) a_2^{(2)} a2(2)的表格:
| x 1 x_1 x1 | x 2 x_2 x2 | z 1 ( 2 ) z_1^{(2)} z1(2) | z 1 ( 2 ) z_1^{(2)} z1(2) | g ( z 2 ( 2 ) ) g(z_2^{(2)}) g(z2(2)) | g ( z 2 ( 2 ) ) g(z_2^{(2)}) g(z2(2)) | a 1 ( 2 ) a_1^{(2)} a1(2) | a 2 ( 2 ) a_2^{(2)} a2(2) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | -15 | 5 | ≈ 0 \approx0 ≈0 | ≈ 1 \approx1 ≈1 | 0 | 1 |
| 0 | 1 | -5 | -5 | ≈ 0 \approx0 ≈0 | ≈ 0 \approx0 ≈0 | 0 | 0 |
| 1 | 0 | -5 | -5 | ≈ 0 \approx0 ≈0 | ≈ 0 \approx0 ≈0 | 0 | 0 |
| 1 | 1 | 5 | -15 | ≈ 1 \approx1 ≈1 | ≈ 0 \approx0 ≈0 | 1 | 0 |
从上表细心的读者应该可以观察出,我们对 a 1 ( 2 ) 、 a 2 ( 2 ) a_1^{(2)}、a_2^{(2)} a1(2)、a2(2)再做一次或操作,得到的结果就是同或了。对的,第二层到第三层 ,做的就是或操作,同样第三层可以得出:
z 1 ( 3 ) = 10 x 1 + 10 x 2 − 5 z_1^{(3)} = 10x_1+10x_2-5 z1(3)=10x1+10x2−5
上面这个式子与上面聊或的式子是同一个的,那么我们就可以得到一个完整的表:
| x 1 x_1 x1 | x 2 x_2 x2 | z 1 ( 2 ) z_1^{(2)} z1(2) | z 1 ( 2 ) z_1^{(2)} z1(2) | g ( z 2 ( 2 ) ) g(z_2^{(2)}) g(z2(2)) | g ( z 2 ( 2 ) ) g(z_2^{(2)}) g(z2(2)) | a 1 ( 2 ) a_1^{(2)} a1(2) | a 2 ( 2 ) a_2^{(2)} a2(2) | z 1 ( 3 ) z_1^{(3)} z1(3) | g ( z 2 ( 3 ) ) g(z_2^{(3)}) g(z2(3)) | a 1 ( 3 ) a_1^{(3)} a1(3) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | -15 | 5 | ≈ 0 \approx0 ≈0 | ≈ 1 \approx1 ≈1 | 0 | 1 | 5 | ≈ 1 \approx1 ≈1 | 1 |
| 0 | 1 | -5 | -5 | ≈ 0 \approx0 ≈0 | ≈ 0 \approx0 ≈0 | 0 | 0 | -5 | ≈ 0 \approx0 ≈0 | 0 |
| 1 | 0 | -5 | -5 | ≈ 0 \approx0 ≈0 | ≈ 0 \approx0 ≈0 | 0 | 0 | -5 | ≈ 0 \approx0 ≈0 | 0 |
| 1 | 1 | 5 | -15 | ≈ 1 \approx1 ≈1 | ≈ 0 \approx0 ≈0 | 1 | 0 | 15 | ≈ 1 \approx1 ≈1 | 1 |
上面是过程的解释,上表的第一行是初始输入,最后一行是最后的输出,比对后正好完成了同或。
所以从上可知,我们对于非线性边界的拟合,单层感知机是完成不了的,需要发展使用多层感知机,同样我们的神经网络与多层感知机的结构是相同的,也都需要用激活函数将线性转化为非线性(从上述例子中也能看出,如果我们不使用激活函数,那么每层都是线性关系,最后的结果也是线性关系,那么就达不到最终的泛化的要求)。
4. 神经网络损失函数
看到此节的读者,默认已经了解了逻辑回归,由于本文中默认使用的激活函数是sigmoid函数,所以可以直接与逻辑回归的损失函数相比较。先给出逻辑回归与神经网络的损失函数:
逻辑回归损失函数(加正则化项):
J ( θ ) = 1 m ( ∑ i = 1 m ( − y ( i ) l n ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) l n ( 1 − h θ ( x ( i ) ) ) ) + λ 2 m ( ∑ j = 1 n θ j 2 ) J(\theta) = \frac{1}{m}(\sum_{i=1}^{m}(-y^{(i)}ln(h_\theta(x^{(i)}))-(1-y^{(i)})ln(1-h_\theta(x^{(i)})))+\frac{\lambda}{2m}(\sum_{j=1}^n\theta_j^2) J(θ)=m1(i=1∑m(−y(i)ln(hθ(x(i)))−(1−y(i))ln(1−hθ(x(i))))+2mλ(j=1∑nθj2)
神经网络损失函数(加正则化项):
J ( θ ) = 1 m [ ∑ i = 1 m ∑ k = 1 K ( − y k ( i ) l n ( h θ ( x ( i ) ) k ) − ( 1 − y k ( i ) ) l n ( 1 − h θ ( x ( i ) ) k ) ) ] + λ 2 m ( ∑ l = 1 L ∑ i = 1 S l ∑ j = 1 S ( l + 1 ) ( θ j i ( l ) ) 2 ) J(\theta) = \frac{1}{m}[\sum_{i=1}^{m}\sum_{k=1}^{K}(-y_k^{(i)}ln(h_\theta(x^{(i)})_k)-(1-y_k^{(i)})ln(1-h_\theta(x^{(i)})_k))]+\frac{\lambda}{2m}(\sum_{l=1}^L\sum_{i=1}^{S_l}\sum_{j=1}^{S_{(l+1)}}(\theta_{ji}^{(l)})^2) J(θ)=m1[i=1∑mk=1∑K(−yk(i)ln(hθ(x(i))k)−(1−yk(i))ln(1−hθ(x(i))k))]+2mλ(l=1∑Li=1∑Slj=1∑S(l+1)(θji(l))2)
其中 h θ ( x ) 输出是 k h_\theta(x)输出是k hθ(x)输出是k维向量, ( h θ ( x ) ) k (h_\theta(x))_k (hθ(x))k表示输出向量的第 k k k个元素,其中k≥3
可以看出两个式子的形式是很像的,由于都是进行分类的模型,而且函数均是sigmoid函数,我们逐一分析一下损失函数的各个组成部分的含义,主要是通过分析各个求和函数的含义与作用:
相信了解逻辑回归的读者,应该都知道 1 m ( ∑ i = 1 m ( − y ( i ) l n ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) l n ( 1 − h θ ( x ( i ) ) ) ) \frac{1}{m}(\sum_{i=1}^{m}(-y^{(i)}ln(h_\theta(x^{(i)}))-(1-y^{(i)})ln(1-h_\theta(x^{(i)}))) m1(∑i=1m(−y(i)ln(hθ(x(i)))−(1−y(i))ln(1−hθ(x(i))))的由来,如果读者直接跳到这来看的神经网络的知识,可以去上文逻辑回归部分的文章回顾一下这部分的推导与含义,这地方不再重新解释,但是神经网络的损失函数在这个基础上多了一个求和,引入了一个新的变量 k k k。
上文中有聊过,逻辑回归是二分类模型,只有两个输出0或1,但实际上神经网络输出的并不一定只是两个,而上式满足的条件就是 k ≥ 3 k≥3 k≥3, k k k的意义就是表示输出的向量的维数,也就是分类的个数,若有四个输出, k = 1 , 2 , 3 , 4 k=1,2,3,4 k=1,2,3,4。
由于逻辑回归只输出1或0,所以我们不需要引入 k k k,直接将真实值与预测出的值相乘即可。对于神经网络来讲,需要将 k k k个输出求和, ∑ i = 1 m ∑ k = 1 K \sum_{i=1}^{m}\sum_{k=1}^{K} ∑i=1m∑k=1K就是代表第 i i i个样本输入特征,通过神经网络得到的 k k k个输出值与第 i i i个样本的真实的 k k k个值代入方程计算后再求和,然后将样本集中所有样本都执行上述相同的操作并求和。实际上还是表达了样本真实值与经过神经网络的输出值之间的差距,从而方便算出误差。
下面再看正则项:
为了方便理解损失函数正则项含义,我们直接举一个例子来看:
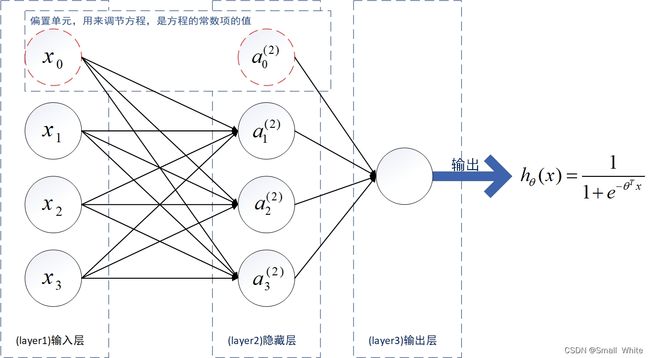
对于: ∑ l = 1 L ∑ i = 1 S l ∑ j = 1 S ( l + 1 ) \sum_{l=1}^L\sum_{i=1}^{S_l}\sum_{j=1}^{S_{(l+1)}} ∑l=1L∑i=1Sl∑j=1S(l+1),先来看一下对应的变量符号是什么意思(注意,在上文中有详细说明含义,这里只是简单复习提醒一下):
l l l 代表层数
j j j 代表 l + 1 l+1 l+1 层(即下一层)的第 j j j 个神经单元
i i i 代表第 l l l 层(即当前层)的第 i i i 个神经单元
θ j i ( l ) \theta_{ji}^{(l)} θji(l)表示从第 l l l 层的第 i i i 个神经元到第 l + 1 l+1 l+1 层的第 j j j 个单元的权重 θ \theta θ
从上图中,我们取 l = 1 l=1 l=1,代表此时只看第一层到第二层之间的 θ \theta θ,我们可以得到:
Θ ( 1 ) = [ θ 10 ( 1 ) θ 11 ( 1 ) θ 12 ( 1 ) θ 13 ( 1 ) θ 20 ( 1 ) θ 21 ( 1 ) θ 22 ( 1 ) θ 23 ( 1 ) θ 30 ( 1 ) θ 31 ( 1 ) θ 32 ( 1 ) θ 33 ( 1 ) ] \Theta^{(1)} = \left[ \begin{matrix} \theta_{10}^{(1)} & \theta_{11}^{(1)} & \theta_{12}^{(1)} & \theta_{13}^{(1)} \\ \theta_{20}^{(1)} & \theta_{21}^{(1)} & \theta_{22}^{(1)} & \theta_{23}^{(1)} \\ \theta_{30}^{(1)} & \theta_{31}^{(1)} & \theta_{32}^{(1)} & \theta_{33}^{(1)} \end{matrix} \right] Θ(1)=⎣ ⎡θ10(1)θ20(1)θ30(1)θ11(1)θ21(1)θ31(1)θ12(1)θ22(1)θ32(1)θ13(1)θ23(1)θ33(1)⎦ ⎤
那么从上面 l = 1 l=1 l=1时,可以得到的矩阵可知 ∑ i = 1 S l ∑ j = 1 S ( l + 1 ) \sum_{i=1}^{S_l}\sum_{j=1}^{S_{(l+1)}} ∑i=1Sl∑j=1S(l+1)代表的就是将矩阵的列先求和,然后行求和,最后得到一个数,说白了就是求这个矩阵的和,然后最外层还有一个 ∑ l = 1 L \sum_{l=1}^L ∑l=1L,这个应该就好理解了,每层的都能求出来一个值,最后相加求和即可,至于为什么求和,若还不太清楚的读者,请回翻到上文中的人工神经网络基础的第一部分从逻辑回到到神经网络部分有关正则化的说明。
5. 神经网络梯度计算
我们先回顾一下神经网络的损失函数:
J ( θ ) = 1 m [ ∑ i = 1 m ∑ k = 1 K ( − y k ( i ) l n ( h θ ( x ( i ) ) k ) − ( 1 − y k ( i ) ) l n ( 1 − h θ ( x ( i ) ) k ) ) ] + λ 2 m ( ∑ l = 1 L ∑ i = 1 S l ∑ j = 1 S ( l + 1 ) ( θ j i ( l ) ) 2 ) J(\theta) = \frac{1}{m}[\sum_{i=1}^{m}\sum_{k=1}^{K}(-y_k^{(i)}ln(h_\theta(x^{(i)})_k)-(1-y_k^{(i)})ln(1-h_\theta(x^{(i)})_k))]+\frac{\lambda}{2m}(\sum_{l=1}^L\sum_{i=1}^{S_l}\sum_{j=1}^{S_{(l+1)}}(\theta_{ji}^{(l)})^2) J(θ)=m1[i=1∑mk=1∑K(−yk(i)ln(hθ(x(i))k)−(1−yk(i))ln(1−hθ(x(i))k))]+2mλ(l=1∑Li=1∑Slj=1∑S(l+1)(θji(l))2)
在线性回归与逻辑回归中,要想求 m i n ( J ( θ ) ) min(J(\theta)) min(J(θ)),要对所有的参数 θ j \theta_j θj求 ∂ J ( θ ) θ j \frac{\partial J(\theta)}{\theta_j} θj∂J(θ),对每个 θ \theta θ求得的偏导值,就是这个 θ \theta θ下降的梯度值,用原来的 θ \theta θ值减去新求的梯度值就是梯度更新。直到我们的损失函数 J ( θ ) J(\theta) J(θ)最后不再减小就相当于了训练好了一个模型,但模型的好坏是需要测试集去评判。
对于神经网络也是同样的,要对每个 θ j i ( l ) \theta_{ji}^{(l)} θji(l)求 ∂ J ( θ ) θ j i ( l ) \frac{\partial J(\theta)}{\theta_{ji}^{(l)}} θji(l)∂J(θ),然后更新各个 θ \theta θ,直到我们的损失函数 J ( θ ) J(\theta) J(θ)最后不再减小。至于求偏导后的形式是什么样和怎么样更新梯度,我们在下面的前向传播与后向传播一起聊一聊。
6. 前向传播与反向传播
① 前向传播
前向传播比较好理解,上面我们从输入层到输出层的计算过程就是正向传播的过程,下面用一个例子在走一遍前向传播的过程:
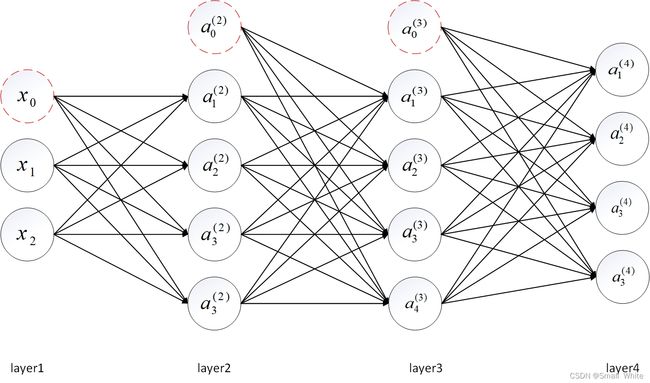
上述为四层网络,下面是前向传播的过程(上标代表层数):
Ⅰ层: a ( 1 ) = x a^{(1)}=x a(1)=x
Ⅱ层: z ( 2 ) = θ ( 1 ) a ( 1 ) z^{(2)} = \theta^{(1)}a^{(1)} z(2)=θ(1)a(1) a ( 2 ) = g ( z ( 2 ) ) a^{(2)} = g(z^{(2)}) a(2)=g(z(2))
Ⅲ层: z ( 3 ) = θ ( 2 ) a ( 2 ) z^{(3)} = \theta^{(2)}a^{(2)} z(3)=θ(2)a(2) a ( 3 ) = g ( z ( 3 ) ) a^{(3)} = g(z^{(3)}) a(3)=g(z(3))
Ⅳ层: z ( 4 ) = θ ( 3 ) a ( 3 ) z^{(4)} = \theta^{(3)}a^{(3)} z(4)=θ(3)a(3) a ( 4 ) = h θ ( x ) = g ( z ( 4 ) ) a^{(4)} = h_\theta(x)= g(z^{(4)}) a(4)=hθ(x)=g(z(4))
上述从Ⅰ → \rightarrow →Ⅱ → \rightarrow →Ⅲ → \rightarrow →Ⅳ就是正向执行的传播过程,其中Ⅰ、Ⅱ、Ⅲ都需要添加偏置项。
②反向传播
了解反向传播前,我们先看一个知识点:前向模式求导和后向模式求导,对理解反向传播有所帮助:
Ⅰ、前向模式求导
假设有一个方程 f ( a , b , c ) = ( a + b ) ∗ ( ( c + 1 ) + b ) f(a,b,c) = (a+b)*((c+1)+b) f(a,b,c)=(a+b)∗((c+1)+b),我们要对参数 b b b求导,应该怎么求呢?我想有些读者可能会用求导法则中的有理运算法则中的 ( u v ) ′ (uv)^{'} (uv)′结合复合函数求导法则来求(或者有的读者也会拆开直接求)。我们现在用前向求导来求一下这个导数。
首先我们用图来表示计算式 f ( a , b , c ) = ( a + b ) ∗ ( ( c + 1 ) + b ) f(a,b,c) = (a+b)*((c+1)+b) f(a,b,c)=(a+b)∗((c+1)+b)
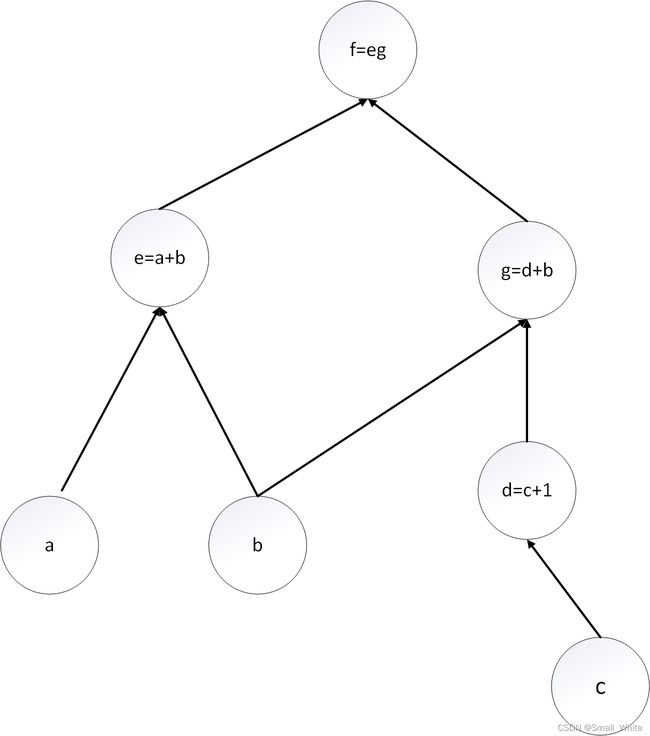
我们假设 a = 5 , b = 3 , c = 1 a=5,b=3,c=1 a=5,b=3,c=1,则我们可以得到各个节点的值:
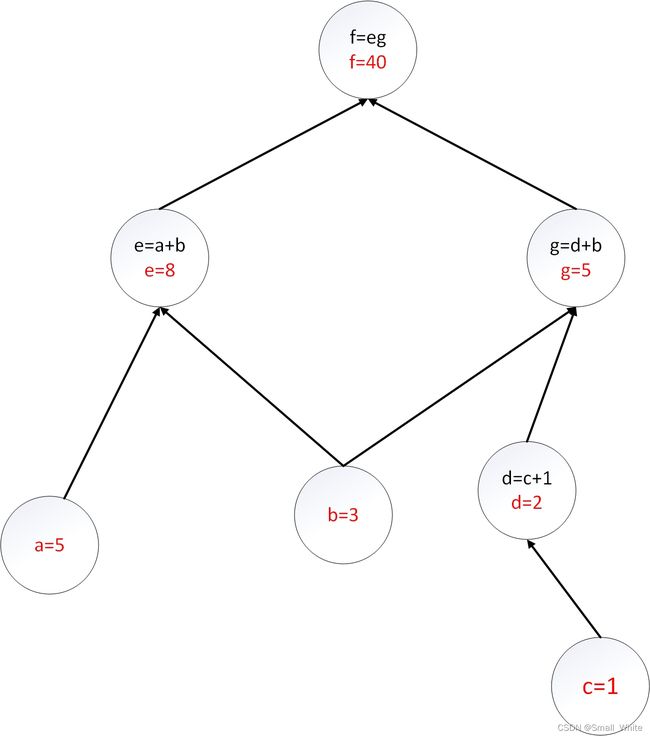
接下来我们对上图路径上的每一个子算式求偏导:
d = c + 1 d = c+1 d=c+1 ∂ d ∂ c = 1 \frac{\partial d}{\partial c}=1 ∂c∂d=1
g = d + b g = d+b g=d+b ∂ g ∂ b = 1 \frac{\partial g}{\partial b}=1 ∂b∂g=1 ∂ g ∂ b = 1 \frac{\partial g}{\partial b}=1 ∂b∂g=1
e = a + b e=a+b e=a+b ∂ e ∂ a = 1 \frac{\partial e}{\partial a}=1 ∂a∂e=1 ∂ e ∂ b = 1 \frac{\partial e}{\partial b}=1 ∂b∂e=1
f = e g f=eg f=eg ∂ f ∂ e = g = 7 \frac{\partial f}{\partial e}=g=7 ∂e∂f=g=7 ∂ f ∂ g = e = 8 \frac{\partial f}{\partial g}=e=8 ∂g∂f=e=8
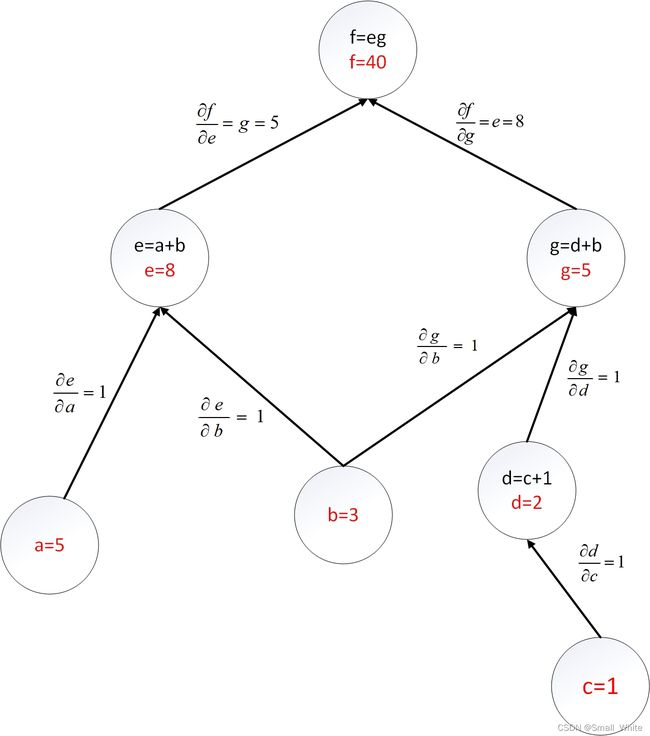
为了方便理解怎么利用上图求导,我们先来看一下导数的定义(同济大学高等数学第七版75页):
定义:设函数 y = f ( x ) y=f(x) y=f(x)在点 x 0 x_0 x0 的某个邻域内有定义,当自变量 x x