一、知识储备
- 本次主要完成了线性回归的经典模型-波士顿房价预测,一共十三个特征,假设函数如下:
h θ ( x ) = [ 1 x 1 1 x 2 1 ⋯ x 13 1 1 x 1 2 x 2 2 ⋯ x 13 2 ⋮ ⋮ ⋯ ⋯ ⋮ 1 x 1 m x 2 m ⋯ x 13 m ] [ θ 0 θ 1 θ 2 ⋮ θ 13 ] (1) h_\theta(x)=\left[ \begin{matrix} 1 & x_1^1 & x_2^1 & \cdots & x_{13}^1 \\ 1 &x_1^2 & x_2^2 & \cdots & x_{13}^2\\ \vdots & \vdots & \cdots & \cdots & \vdots\\ 1 &x_1^m & x_2^m & \cdots & x_{13}^m \end{matrix} \right]\left[ \begin{matrix} \theta_0 \\ \theta_1 \\ \theta_2 \\ \vdots \\ \theta_{13} \end{matrix} \right]\tag{1} hθ(x)=⎣⎢⎢⎢⎡11⋮1x11x12⋮x1mx21x22⋯x2m⋯⋯⋯⋯x131x132⋮x13m⎦⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎡θ0θ1θ2⋮θ13⎦⎥⎥⎥⎥⎥⎤(1)
也可以表达成函数形式,读者可自行转化,较为简单。
- 批量梯度下降
批量梯度下降的相关知识请读者去看线性回归系列的第一篇文章,这里不详细介绍相关知识,下面主要介绍一下怎么实现正则化(关于需要正则化原因请看线性回归系列的第二篇),来减少高阶、维度高对拟合、模型的影响,添加的地方有损失函数与梯度下降函数:
J ( θ ) = 1 2 m ( ∑ i = 0 m ( h θ ( x ( i ) ) − y ( i ) ) 2 ) + λ 2 m ∑ j = 1 n θ j 2 J(\theta)=\frac{1}{2m}(\sum_{i=0}^m(h_\theta(x^{(i)})-y^{(i)})^2)+\frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2 J(θ)=2m1(i=0∑m(hθ(x(i))−y(i))2)+2mλj=1∑nθj2
实际上上式是可以合并的,为了读者更容易理解,写开了形式。注意:我们规定进行正则化时的 θ \theta θ 是从1开始的,也就是只有特征的系数才会参与正则化。 λ \lambda λ 的作用是维护损失函数与正则化参数之间的平衡关系,更好的去拟合训练集的目标和将参数控制得更小的目标,保持假设模型的相对简单。
有读者应该现在已经明白了下一个需要改变的地方,是的,我们的 J ( θ ) J(\theta) J(θ)发生了改变,那么我们梯度下降的减数项也应该发生变化,因为减数项时通过 J ( θ ) J(\theta) J(θ)求导得来的(这块有问题的请移步到线性回归第一篇,梯度下降的知识点)
θ j : = θ j − 1 m ( ∑ i = 0 m ( h θ ( x ( i ) ) − y ( i ) ) x ( i ) + λ θ j ) \theta_j:=\theta_j - \frac{1}{m}(\sum_{i=0}^m(h_\theta(x^{(i)})-y^{(i)})x^{(i)}+\lambda\theta_j) θj:=θj−m1(i=0∑m(hθ(x(i))−y(i))x(i)+λθj)
上面就是加上正则化变化的地方,建议读者从第一篇看过来,这样应该不会有什么障碍,如果哪地方有错或说的不详细,欢迎大家留言。
二、代码实现
- 读取与处理数据、拟合图、误差图代码,文件名:
housegradient.p
from ftplib import error_reply
import imp
from math import ceil
from pydoc import doc
from turtle import right, shape
import numpy as np
import matplotlib.pyplot as plt
from housegradient import gradientFun
theta = np.array([0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,0.1,0.2,0.3,0.4])
theta_0 = 0.5
lamda = 0.02
origin_data = np.loadtxt(fname='housing.data')
np.random.shuffle(origin_data)
trans_data = origin_data[0:int(0.8*(np.size(origin_data)/14))]
test_data = origin_data[-ceil(0.2*(np.size(origin_data)/14)):]
trans_data_std = np.std(trans_data[:,0:13],axis=0)
trans_data_std = np.insert(trans_data_std,13,values=[1],axis=0)
trans_data_average = np.mean(trans_data[:,0:13],axis=0)
trans_data_average = np.insert(trans_data_average,13,values=[0],axis=0)
trans_data_handled = (trans_data-trans_data_average)/trans_data_std
trans_data_y = trans_data_handled[:,-1]
error_array_j = np.array([])
for i in range(100):
if i !=0:
np.random.shuffle(trans_data_handled)
trans_data_x = trans_data_handled[:,0:13]
trans_data_y = trans_data_handled[:,-1]
current_tran_ones = np.ones((1,np.size(trans_data_y)))
trans_data_x_batch = np.array_split(trans_data_x,10)
trans_data_y_batch = np.array_split(trans_data_y,10)
for j in range(10):
current_trans_data_x = trans_data_x_batch[j]
current_trans_data_y = trans_data_y_batch[j]
y = np.dot(theta,current_trans_data_x.T)+theta_0
error_array = y-current_trans_data_y
theta,theta_0= gradientFun(current_trans_data_x,error_array,theta,theta_0=theta_0,lamda=lamda)
error_y = (np.dot(theta,trans_data_x.T)+theta_0) - trans_data_y
error_j = (np.dot(error_y,error_y.T)+lamda*np.dot(theta,theta.T))/(2*np.size(trans_data_y))
error_array_j=np.concatenate((error_array_j,np.array([error_j])),axis=0)
index = np.arange(0,np.size(error_array_j)).reshape(np.size(error_array_j))
plt.plot(index,error_array_j)
plt.show()
test_data_std = np.std(test_data[:,0:13],axis=0)
test_data_std = np.insert(test_data_std,13,values=[1],axis=0)
test_data_average = np.mean(test_data[:,0:13],axis=0)
test_data_average = np.insert(test_data_average,13,values=[0],axis=0)
test_data_handled = (test_data-test_data_average)/test_data_std
test_data_x = test_data_handled[:,0:13]
test_data_y = test_data_handled[:,-1]
error_test_y = (np.dot(theta,test_data_x.T)+theta_0) - test_data_y
index = np.arange(0,np.size(error_test_y)).reshape(np.size(error_test_y))
error_j = np.dot(error_test_y,error_test_y.T)/(2*np.size(test_data_y))
print(error_test_y)
plt.figure()
plt.plot(index,error_test_y)
plt.show()
- 下面是梯度下降函数,文件名为:
housegradient.py
import numpy as np
def gradientFun(x,error_array,theta,theta_0,lamda):
alpha = 0.006
theta_0 = theta_0 - alpha * (np.sum(error_array)/np.size(error_array))
theta = theta - alpha * ((np.dot(error_array,x)+lamda*theta.T)/np.size(error_array))
print('损失为{}'.format(error_array))
print('\ntheta的值为{}'.format(theta))
print('theta_0的值为{}'.format(theta_0))
return theta,theta_0
下图是误差函数的图像:
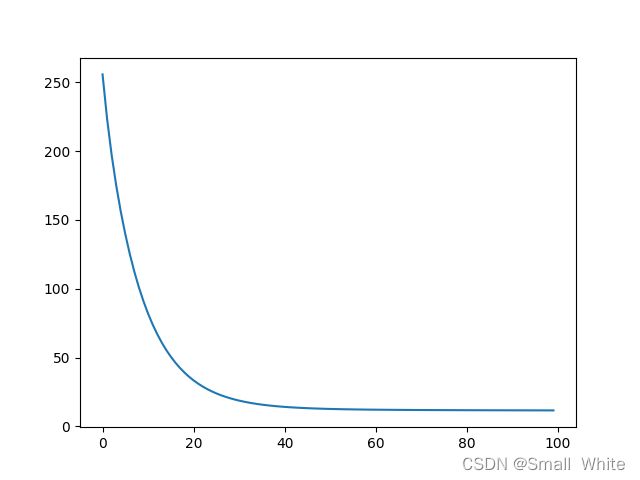
下图是测试集的误差,基本在-5~5之间
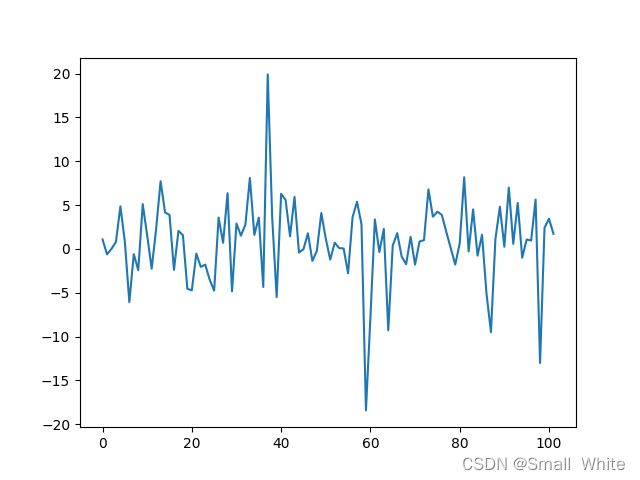
以上若有问题,请大佬指出,感激不尽,共同进步。

