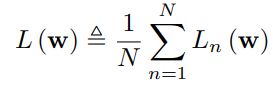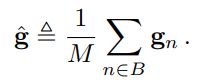神经网络 泛化
介绍 (Introduction)
Deep learning architectures such as recurrent neural networks and convolutional neural networks have seen many significant improvements and have been applied in the fields of computer vision, speech recognition, natural language processing, audio recognition and more. The most commonly used optimization method for training highly complex and non-convex DNNs is stochastic gradient descent (SGD) or some variant of it. DNNs however typically have some non-convex objective functions which are a bit difficult optimize with SGD. Thus, SGD, at best, finds a local minimum of this objective function. Although the solutions of DNNs are a local minima, they have produced great end results. The 2015 paper The Loss Surfaces of Multilayer Networks by Choromanska et al. showed that as the number of dimensions increases, the difference between local minima decreases significantly, and, therefore, the existence of “bad” local minima decreases exponentially.
诸如递归神经网络和卷积神经网络之类的深度学习架构已取得了许多重大改进，并已应用于计算机视觉，语音识别，自然语言处理，音频识别等领域。 训练高度复杂和非凸DNN的最常用优化方法是随机梯度下降(SGD)或它的某些变体。 但是，DNN通常具有一些非凸目标函数，而使用SGD进行优化则有些困难。 因此，SGD充其量只能找到该目标函数的局部最小值。 尽管DNN的解决方案是局部最小值，但它们产生了很好的最终结果。 2015年论文《多层网络的损失面》 由Choromanska等人撰写。 结果表明，随着维数的增加，局部极小值之间的差异显着减小，因此，“不良”局部极小值的存在呈指数下降。
In the 2018 Israel Institute of Technology paper we will primarily examine in this article, Train Longer, Generalize Better: Closing the Generalization Gap in Large Batch Training of Neural Networks, Hoffer et al. address a well-known phenomenon regarding large batch sizes during training and the generalization gap. That is, when a large batch size is used while training DNNs, the trained models appear to generalize less well. This observation remains true even when the models are trained “without any budget or limits, until the loss function ceased to improve” (Keskar et al., 2017).
在2018年以色列理工学院的论文中，我们将主要在本文中研究更长的训练，更好地推广：缩小大批量神经网络训练中的推广差距 ，Hoffer等。 解决了关于训练期间大批量和普遍性差距的众所周知的现象。 也就是说，当在训练DNN时使用大批量时，训练后的模型似乎推广得不太好。 即使“在没有任何预算或限制的情况下训练模型，直到损失函数停止改善”，这一观察仍然是正确的(Keskar等，2017)。
The generalization gap is an important concept for understanding generalization. It is commonly defined as the difference between a model’s performance on training data and its performance on unseen data drawn from the same distribution. Significant strides have been made toward deriving better DNN generalization bounds. This is because understanding the origin of the generalization gap, and moreover, finding ways to decrease it, may have a significant practical importance.
泛化差距是理解泛化的重要概念。 通常将其定义为模型在训练数据上的性能与从同一分布中提取的看不见的数据上的性能之间的差异。 在推导更好的DNN泛化界限方面已取得了重大进展。 这是因为理解泛化鸿沟的根源，并且找到减少这种鸿沟的方法可能具有重大的实践意义。
Hoffer et al. study the above phenomenon in their paper. They examine the initial high learning rate training phase and propose that this phase can be described using a high-dimensional “random walk on a random potential” process, with an “ultra-slow” logarithmic increase in the distance of the weights from their initialization. The authors observed the following,
Hoffer等。 在他们的论文中研究上述现象。 他们研究了初始的高学习率训练阶段，并建议可以使用高维“随机势随机游走”过程来描述该阶段，权重从其初始化开始的距离对数增加“超慢” 。 作者观察到以下内容：
- by simply adjusting the learning rate and batch normalization, the generalization gap can be significantly decreased, 通过简单地调整学习率和批量归一化，可以大大减少泛化差距，
- generalization, what is the model’s ability to adapt properly to new, previously unseen data, keeps improving for a long time at the initial high learning rate, even without any observable changes in training or validation errors, and 泛化，即模型在最初的高学习率下能够正确地适应新的，以前看不见的数据的能力，可以在很长一段时间内持续改进，即使训练或验证错误没有任何可观察到的变化，并且
- there is no inherent “generalization gap”, i.e., large-batch training can generalize as well as small-batch training by adapting the number of iterations. 没有固有的“概化鸿沟”，即大批量训练可以通过调整迭代次数来概括小批量训练。
Therefore, the authors concluded empirically that the “generalization gap” stems from the relatively small number of updates rather than the batch size itself, and can be completely eliminated by adapting the training regime used.
因此，作者凭经验得出结论，“一般化差距”源于相对较少的更新次数，而不是批次数量本身，并且可以通过调整所使用的训练方法来完全消除。
We will look at these findings in more detail in the rest of this article.
我们将在本文的其余部分中更详细地研究这些发现。
大量培训，背景 (Training with a large batch, background)
Training method setupTypically when training DNNs, the learning rate and momentum term are perturbed over time, usually with an exponential decrease every few epochs of training data. Another common approach is to use a “regime” adaptive parameter method. This is done by defining the regimes the optimization process is in. These regimes define intervals for which the learning rates are constant during the entirety of the regime.
训练方法的设置通常，在训练DNN时，学习率和动量项会随着时间的推移而受到干扰，通常每隔几个训练数据周期就会呈指数下降。 另一种常见的方法是使用“系统”自适应参数方法。 这是通过定义优化过程所处的机制来完成的。这些机制定义了在整个机制中学习率恒定的时间间隔。
Hoffer et al. examine a fixed learning rate (within a certain regime) that decreases exponentially every few epochs. Here the number of epochs is related to the regime the training process is in. As a side note, the convergence of SGD is known to be affected by the batch size (Li et al., 2014), but the authors here only focus on generalization. The experiments were carried out using the Resnet44 topology, introduced by He et al. (2016).
Hoffer等。 检查固定的学习率(在一定范围内)，该学习率每隔几个时期呈指数下降。 这里的时期数与训练过程所处的机制有关。作为一个侧面说明，已知SGD的收敛受批次大小的影响(Li等人，2014)，但本文的作者仅关注概括。 实验是使用He等人介绍的Resnet44拓扑进行的。 (2016)。
Empirical observations from previous workPrevious work by Keskar et al. (2017) studied the performance and properties of models trained with relatively large batches and reported the following observations:
来自先前工作的经验观察 Keskar等人的先前工作 。 (2017)研究了相对较大批次训练的模型的性能和特性，并报告了以下观察结果：
- Training models with large batch sizes increased the generalization error. 大批量的训练模型会增加泛化误差。
- The “generalization gap” did not go away even when the models were trained without limits — that is, until the loss function stops improving. 即使对模型进行了无限制的训练，“归纳差距”也不会消失，也就是说，直到损失函数停止改善。
- Low generalization was correlated with “sharp” minima (strong positive curvature), while good generalization was correlated with “flat” minima (weak positive curvature). 低泛化与“锐利”最小值(强正曲率)相关，而泛化良好与“平坦”极小值(弱正曲率)相关。
- Small-batch regimes were briefly noted to produce weights that are farther away from the initial point, in comparison with the weights produced in a large-batch regime. 简要指出，与大批量生产方式产生的权重相比，小批量生产方式产生的权重距离起始点更远。
理论分析 (Theoretical analysis)
NotationThis paper examines DNNs trained with SGD. Let N denote the number of samples which the DNN is trained on, w the vector of the neural network parameters, and L_n(w) the loss function on sample n. The value w is determined by minimizing the loss function L(w) as defined in Equation (1).
表示法本文研究了使用SGD训练的DNN。 令N表示训练DNN的样本数，其中w是神经网络参数的向量，而L_n(w)表示样本n的损失函数。 通过最小化方程(1)中定义的损耗函数L(w)来确定值w。
SGD will compute the negative gradient of the loss function L(w) and use it as the descent direction. The gradient is shown in Equation (2).
SGD将计算损失函数L(w)的负梯度，并将其用作下降方向。 梯度如公式(2)所示。
where g is the true gradient, and g_n is the per-sample gradient. During training, we increment the parameter vector w using only the mean gradient gˆ computed on some mini-batch B, i.e., a set of M randomly selected sample indices as defined in Equation (3).
其中g是真实的渐变，g_n是每个样本的渐变。 在训练过程中，我们仅使用在某些小批量B上计算出的平均梯度gˆ来增加参数矢量w，即在等式(3)中定义的M个随机选择的样本索引的集合。
The authors examine the simplest form of SGD training, in which the weights at update step t are incremented according to the mini-batch gradient ∆w_t = η gˆ_t. In addition, the increments are uncorrelated between different mini-batches. Here is where the idea of a random walk comes into play. We can think of the weight vector w_t as a particle performing a random walk on the loss surface of L(w_t). Furthermore, adding the momentum term can be thought of as providing the particle with inertia.
作者研究了SGD训练的最简单形式，其中更新步骤t的权重根据小批量梯度Δw_t=ηgˆ_t递增。 另外，不同的小批量之间的增量是不相关的。 这是随机游走的想法发挥作用的地方。 我们可以将权重向量w_t视为在L(w_t)的损失面上执行随机游动的粒子。 此外，添加动量项可以认为是为粒子提供了惯性。
Motivation of random walk model and empirical observationsThe reason behind the use of a random walk intuition has to do with the fact that the shape/surface of the loss function in DNNs cannot be determined. Statistical models and tools are commonly used to formulate a simpler description of the loss function as a random process, and therefore, the motivation for using a random walk.
随机游动模型的动机和经验观察使用随机游动直觉背后的原因与以下事实有关：无法确定DNN中损失函数的形状/表面。 统计模型和工具通常用于将损失函数描述为一个随机过程，因此是使用随机游走的动机。
In addition, “random walk on a random potential (loss)” is a field that has been studied extensively. Bouchaud & Georges, in 1990, showed that the asymptotic behaviour of the auto-covariance of a random potential,
另外，“随机游走于随机势(损失)”是已被广泛研究的领域。 Bouchaud＆Georges在1990年发现，随机势的自协方差的渐近行为
in a certain range, determines the asymptotic behaviour of the random walker in that range:
在某个范围内，确定该随机游走器在该范围内的渐近行为：
This is called an “ultra-slow diffusion” in which, typically || w_t — w_0 || ~ log(t)^(2/α). In other words, the mean square displacement grows logarithmically with time. From a training point of view, this behaviour tells us that the weight distance from the initialization point increases logarithmically with the number of training iterations (weight updates).
这称为“超慢扩散”，其中通常||。 w_t — w_0 || 〜log(t)^(2 /α)。 换句话说，均方位移随时间呈对数增长。 从训练的角度来看，这种行为告诉我们，距初始化点的权重距离与训练迭代次数(权重更新)成对数增加。
The authors found, empirically, that the value of α = 2. Moreover, the authors found that for all batch sizes, a very similar logarithmic graph is observed. However, different graphs for different batch sizes seem to have somewhat different slopes. This indicates a somewhat different diffusion rate for different batch sizes. Another observation was that smaller batch sizes entail more training iterations in total. Thus, there is a significant difference in the number of iterations and the corresponding weight distance reached at the end of the initial learning phase.
作者根据经验发现α= 2的值。此外，作者发现对于所有批次大小，都可以观察到非常相似的对数图。 但是，针对不同批次大小的不同图表似乎具有一些不同的斜率。 这表明对于不同的批次大小，扩散速率有所不同。 另一个观察结果是，较小的批次大小总计需要进行更多的训练迭代。 因此，迭代次数和在初始学习阶段结束时达到的相应权重距离存在很大差异。
This leads to the following informal argument (which assumes flat minima are indeed important for generalization). During the initial training phase, to reach a minima of “width” d the weight vector w_t has to travel at least a distance d, and this takes a long time, which is about exp(d) iterations. Thus, to reach wide/flat minima we need to have the highest possible diffusion rates (which do not result in numerical instability) and a large number of training iterations.
这导致了以下非正式论证(假设平坦极小值对于泛化确实很重要)。 在初始训练阶段，权重向量w_t要达到“宽度” d的最小值，必须至少传播距离d，这需要很长时间，大约需要exp(d)次迭代。 因此，要达到宽/平坦的最小值，我们需要具有尽可能高的扩散速率(不会导致数值不稳定)和大量的训练迭代。
These observations are what drove the paper’s contribution. It was previously thought that large batch-sizes would result in generalization gaps. However, these observations provide evidence that training with large batch can be done without suffering from performance degradation.
这些发现推动了论文的发展。 以前认为，大批量会导致泛化缺口。 但是，这些观察结果提供了可以进行大批量训练而不会导致性能下降的证据。
不同小批量的匹配重量增加统计 (Matching weight increment statistics for different mini-batch sizes)
First, to correct the different diffusion rates observed for different batch sizes, the paper matches the statistics of the weight increments to that of a small batch size. It does so by increasing the learning rate by the square root of the mini-batch size. The reasoning behind this decision is to have the weight updates in SGD be proportional to the estimated gradient, i.e., ∆w ∝ ηg^, where η is the learning rate. Furthermore, the covariance matrix of the parameter update step ∆w is defined in Equation (4).
首先，为了校正针对不同批次大小观察到的不同扩散率，本文将重量增量的统计信息与小批量的统计值进行了匹配。 通过以最小批量的平方根增加学习率来实现。 该决定背后的理由是使SGD中的权重更新与估计的梯度成比例，即Δw∝ηg^，其中η是学习率。 此外，在等式(4)中定义了参数更新步骤Δw的协方差矩阵。
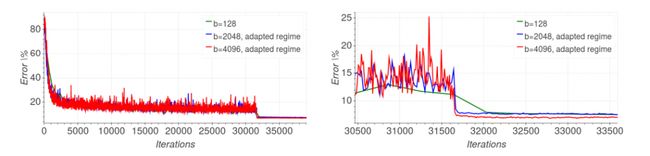
Thus, we can see that in order to make the coefficient η²/M = 1 so that the covariance matrix of the weight update step remains constant for all mini-batch sizes, η must be chosen to be the square root of the mini-batch size M. By implementing this adaptive learning rate scheme, the results of ||w_t − w_0|| between the different batch sizes during the initial training phase show similar slopes. This is displayed in Figure 1.
因此，我们可以看到，为了使系数η²/ M = 1，以使权重更新步骤的协方差矩阵对于所有小批量都保持恒定，必须选择η作为小批量的平方根通过实施这种自适应学习率方案，结果|| w_t − w_0 || 在初始训练阶段，不同批次大小之间的斜率相似。 如图1所示。
A few things to note here is that by increasing the learning rate, the mean steps E[∆w] will also increase. However, the authors found that this effect is negligible since E[∆w] is typically orders of magnitude lower than the standard deviation. This is somewhat intuitive as the update steps in descent methods are generally very small perturbations rather than large changes, i.e., during each update step, the algorithm tweaks the weights by a small amount and evaluates the new value of the loss function.
这里要注意的几件事是，通过提高学习率，平均步长E [∆w]也将增加。 但是，作者发现这种影响可以忽略不计，因为E [Δw]通常比标准偏差低几个数量级。 这在某种程度上是直观的，因为下降方法中的更新步骤通常是很小的扰动，而不是较大的变化，即，在每个更新步骤中，算法都会对权重进行少量调整并评估损失函数的新值。
Hoffer et al. also take into account the influence of batch normalization. Since each per-sample gradient g_n (Equation (3)) depends on the selected mini-batch. In addition, when working with batch-related gradient descent, the updates at the end of the training epoch require the additional complexity of accumulating prediction errors across all training examples. Hoffer et al. takes this into consideration and proposes a method called Ghost Batch Normalization to address this problem.
Hoffer等。 还应考虑批处理规范化的影响。 由于每个样本梯度g_n(等式(3))取决于所选的小批量。 此外，当使用批次相关的梯度下降时，训练时期末尾的更新要求在所有训练示例中累积预测误差的额外复杂性。 Hoffer等。 考虑到这一点，并提出了一种称为Ghost Batch Normalization的方法来解决此问题。
Ghost Batch NormalizationGeneral Batch Normalization (BN) approaches in neural networks form perform normalization on their inputs and have a learnable mean and standard deviation. In the work on BN by Ioffe & Szegedy in 2015, the mean and variance are to be calculated for each channel or feature map separately across a mini-batch of data. For example, in a convolutional layer, the mean and variance are computed across all spatial locations and training examples in a mini-batch. Naturally, BN uses the batch statistics that depend on the chosen batch size.
神经网络中的Ghost批处理规范化通用批处理规范化(BN)方法在其输入上执行规范化，并具有可学习的均值和标准差。 在Ioffe＆Szegedy在2015年进行的BN研究中，将分别在一个小批量数据中分别为每个通道或特征图计算均值和方差。 例如，在卷积层中，均值和方差是在微型批处理中跨所有空间位置和训练示例计算的。 自然，BN使用取决于所选批次大小的批次统计信息。
Hoffer et al. propose theGhost Batch Normalization(GBN) method, which acquires the statistics on small virtual (“ghost”) batches instead of the real large batch. This has been observed to reduce the generalization error. In addition, the authors note that it is important to use the full batch statistic as suggested by Ioffe & Szegedy in 2015 for the inference phase. This is similar to the normal BN method where during inference, the statistics of each mini-batch are replaced with an exponential moving average of the mean and variance. This is to make inference behaviour independent of inference batch statistics.
Hoffer等。 提出了“鬼批标准化”(GBN)方法，该方法获取小虚拟(“鬼”)批而不是真实大批的统计信息。 已经观察到这减少了泛化误差。 此外，作者指出，重要的是使用Ioffe＆Szegedy在2015年提出的用于推断阶段的完整批处理统计信息。 这类似于普通的BN方法，在推理过程中，每个小批量的统计信息将被均值和方差的指数移动平均值所代替。 这是为了使推理行为独立于推理批统计。
The GBN algorithm is given in Algorithm 1 below.
GBN算法在下面的算法1中给出。
It can be seen that the algorithm consists of calculating normalization statistics on disjoint subsets of each training batch. Specifically, with an overall batch size of B_L and a “ghost” batch size of B_S such that B_S evenly divides B_L, the normalization statistics are calculated as
可以看出，该算法包括计算每个训练批次的不相交子集的归一化统计量。 具体来说，如果总批次大小为B_L，“重影”批次大小为B_S，以使B_S均分B_L，则归一化统计量计算为
The authors conclude that this form of batch norm update helps generalization and yields better results than computing the batch-norm statistics over the entire batch. In addition, they found that implementing both the adaptive learning rate and GBN adjustments improves generalization performance.
作者得出的结论是，这种形式的批处理规范更新比在整个批处理中计算批处理规范统计信息更有助于概括并产生更好的结果。 此外，他们发现同时实施自适应学习率和GBN调整可以提高泛化性能。
There is no clear explanation as to why GBN achieves this benefit, but some intuition can be reasoned. I think the following may provide an intuition into why it works: The methodology of GBN can be thought of as another form of regularization. That is, due to the stochasticity in normalization statistics caused by the random selection of mini-batches during training, Batch Normalization causes the representation of a training example to randomly change every time it appears in a different batch of data. Ghost Batch Normalization, by decreasing the number of examples that the normalization statistics are calculated over, increases the strength of this stochasticity, thereby increasing the amount of regularization.
对于GBN为何能获得此好处，目前尚无明确的解释，但可以凭直觉来推理。 我认为以下内容可以直观地说明其工作原理：GBN的方法可以认为是另一种形式的正则化。 也就是说，由于在训练过程中随机选择小批处理而导致的归一化统计数据的随机性，批次归一化会导致训练示例的表示每次出现在不同批次的数据中时都会随机更改。 鬼批处理归一化通过减少计算归一化统计信息所依据的示例数，可以提高这种随机性的强度，从而增加正则化的数量。
调整权重更新的数量可消除泛化差距 (Adapting the number of weight updates eliminates generalization gap)
Hoffer et al. stated that the initial training phase with a high-learning rate enables the model to reach farther locations in the parameter space, which may be necessary to find wider local minima and better generalization. As per Figure 1 (right)., the authors proceeded to match the graphs for different batch sizes by increasing the number of training iterations in the initial high-learning rate regime. They noticed that the distance between the current weight and the initialization point could be a good measure to determine when to decrease the learning rate.
Hoffer等。 指出，具有较高学习率的初始训练阶段使模型可以到达参数空间中的其他位置，这对于找到更广泛的局部最小值和更好的泛化可能是必需的。 如图1(右)所示，作者通过增加初始高学习率体制中的训练迭代次数，来对不同批次的图形进行匹配。 他们注意到，当前权重与初始化点之间的距离可能是确定何时降低学习率的好方法。
Typically, learning rate adaptive algorithms decrease the learning rate after the validation error appears to reach a plateau. This practice is due to the long-held belief that the optimization process should not be allowed to decrease the training error when the validation error plateaus to avoid over-fitting. However, Hoffer et al. observed that substantial improvement to the final accuracy can be obtained by continuing the optimization using the same learning rate even if the training error decreases while the validation plateaus. Subsequent learning rate drops resulted, with a sharp validation error decrease and better generalization for the final model. This is displayed in Figure 2.
通常，学习率自适应算法会在验证错误似乎达到平稳之后降低学习率。 这种做法是由于长期以来的信念，即当验证误差达到稳定水平以避免过度拟合时，不应允许优化过程减少训练误差。 但是，Hoffer等。 他指出，即使训练误差在验证平稳期减少的情况下，通过使用相同的学习率继续优化也可以使最终精度大大提高。 随后导致学习率下降，验证误差急剧下降，最终模型的通用性更好。 如图2所示。
From these observations, Hoffer et al. concluded that the “generalization gap” phenomenon stems from the relatively small number of updates rather than the batch size. Thus, the authors adapted the training regime to better suit the usage of large mini-batches by modifying the number of epochs according to the mini-batch size used. This modification ensures that the number of optimization steps taken is identical to those performed in the small-batch regime and in turn, eliminates the generalization gap.
从这些观察，霍弗等。 结论是“普遍差距”现象源于相对较少的更新，而不是批量大小。 因此，作者根据所使用的小批量大小修改了时期的数量，从而使训练方案更适合大型小批量的使用。 此修改可确保所采取的优化步骤的数量与小批量方案中执行的优化步骤的数量相同，从而消除泛化差距。
实验结果 (Experimental results)
To validate their findings, the authors experimented with the set of image classification tasks listed below.
为了验证他们的发现，作者尝试了下面列出的一组图像分类任务。
- MNIST (LeCun et al., 1998b) — Consists of a training set of 60K and a test set of 10K 28 × 28 gray-scale images representing digits ranging from 0 to 9. MNIST(LeCun等，1998b)—由60K的训练集和10K的测试集组成，这些数字代表从0到9的数字的28×28灰度图像。
- CIFAR-10 and CIFAR-100 (Krizhevsky, 2009) — Each consists of a training set of size 50K and a test set of size 10K. Instances are 32 × 32 colour images representing 10 or 100 classes. CIFAR-10和CIFAR-100(克里日夫斯基，2009年)—每个都由大小为50K的训练集和大小为10K的测试集组成。 实例是代表10或100类的32×32彩色图像。
- ImageNet classification task Deng et al. (2009) — Consists of a training set of size 1.2M samples and test set of size 50K. Each instance is labelled with one of 1000 categories. ImageNet分类任务Deng等。 (2009)—包括大小为1.2M的样本训练集和大小为50K的测试集。 每个实例都标记有1000个类别之一。
In each of the experiments, the authors used the training regime suggested by the original work, together with a momentum SGD optimizer. They defined a batch of 4096 samples as a large batch (LB) and a small batch (SB) was defined as either 128 or 256 samples. The authors then compared the original training baseline for small and large batches, as well as the methods proposed in this paper.
在每个实验中，作者使用了原始工作建议的训练方案以及动量SGD优化器。 他们将一批4096个样本定义为一个大批次(LB)，将一个小批次(SB)定义为128个或256个样本。 然后，作者比较了小批量和大批量的原始培训基准，以及本文提出的方法。
- Learning rate tuning (LB+LR): Using a large batch, while adapting the learning rate to be larger (than that of the small batch) 学习速率调整(LB + LR)：使用大批量，同时将学习速率调整为更大(比小批量)
- Ghost batch norm (LB+LR+GBN): Additionally using the “Ghost batch normalization” method in the training procedure. The “ghost batch size” used is 128. 鬼批处理规范(LB + LR + GBN)：在训练过程中另外使用“鬼批处理归一化”方法。 使用的“幽灵批处理大小”为128。
- Regime adaptation: Using the tuned learning rate as well as ghost batch-norm, but with an adapted training regime. The training regime is modified to have the same number of iterations for each batch size used — effectively multiplying the number of epochs by the relative size of the large batch. 体制适应：使用调整后的学习率以及虚幻批处理规范，但采用适应的培训机制。 修改了训练方式，以使所使用的每个批次大小具有相同的迭代次数-有效地将时期数乘以大批次的相对大小。
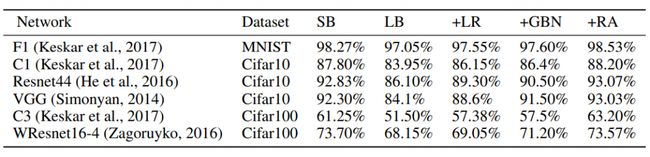
The empirical results supported the paper’s main claim that there is no inherent generalization problem with training using large mini batches. This is shown in Table 1.
实证结果支持了本文的主要主张，即使用大型微型批次进行训练时没有固有的泛化问题。 如表1所示。
We can see that there is a visible generalization gap between using a small batch (SB) versus a large batch (LB). However, the methods proposed in this paper can significantly improve the validation accuracy to the point where the generalization gap completely disappears. Furthermore, in some cases the final validation accuracy is seen to be even better than the one obtained when using a small batch.
我们可以看到，使用小批量(SB)与大批量(LB)之间存在明显的概括差距。 但是，本文提出的方法可以将验证准确性显着提高到泛化差距完全消失的程度。 此外，在某些情况下，最终的验证准确性似乎比使用小批量时获得的准确性更高。
结论 (Conclusion)
The Hoffer et al. paper addresses one of the commonly known phenomena in training deep learning models: training with large batch size results in worse generalization compared to small batch sizes.
霍弗等。 本文讨论了深度学习模型训练中的一种常见现象：与小批量相比，大批量训练导致泛化效果差。
The paper modelled the “movement” on the loss surface as a random walk and studied the relationship of its diffusion rate to the size of a batch. This model provided the empirical observations which allowed Hoffer et al. to propose an adaptive learning rate scheme that depends on the batch size (the learning rate is chosen to be the square root of the mini-batch size). In addition, the authors proposed a novel Ghost Batch Normalization scheme which computes batch-norm statistics over several partitions (“ghost batch-norm”). Ghost Batch Normalization is beneficial for most batch sizes (bigger than the size of a “small batch”), has no computational overhead, is straightforward to tune, and can be potentially used in combination with inference example weighing to great effect. Finally, the authors proposed the use of a sufficient number of high learning rate training iterations.
该论文将损失表面上的“运动”建模为随机游动，并研究了其扩散率与批次大小之间的关系。 该模型提供了Hoffer等人的经验观察。 提出一种取决于批次大小的自适应学习率方案(将学习率选择为小批量大小的平方根)。 此外，作者提出了一种新颖的Ghost Batch Normalization方案，该方案可计算多个分区上的批处理规范统计数据(“ ghost batch-norm”)。 Ghost批处理规范化对大多数批处理大小(大于“小批处理”的大小)都是有益的，没有计算开销，易于调整，并且有可能与推理示例权重结合使用，从而产生很大的效果。 最后，作者建议使用足够数量的高学习率训练迭代。
The experiments carried out in this paper showed that it is indeed possible to enable training with large batches without suffering performance degradation, and that the generalization problem is not related to the batch size but rather to the amount of updates. This contribution re-examines the common belief that large batch sizes will result in poor generalization and provides methods for closing the generalization gap.
本文进行的实验表明，确实有可能在不影响性能的情况下进行大批量训练，并且泛化问题与批量大小无关，而与更新量有关。 此贡献重新检验了大批量将导致较差的泛化的普遍观点，并提供了缩小泛化差距的方法。
The paper Train Longer, Generalize Better: Closing the Generalization Gap in Large Batch Training of Neural Networks is on arXiv.
论文《 更长的时间，更好的推广：在神经网络的大批量训练中弥合差距》在 arXiv上 。
Analyst: Joshua Chou | Editor: H4O; Michael Sarazen
分析员 ：周s | 编辑 ：H4O; 迈克尔·萨拉森(Michael Sarazen)
Synced Report | A Survey of China’s Artificial Intelligence Solutions in Response to the COVID-19 Pandemic — 87 Case Studies from 700+ AI Vendors
同步报告| 针对COVID-19大流行的中国人工智能解决方案的调查-来自700多家AI供应商的87个案例研究
This report offers a look at how China has leveraged artificial intelligence technologies in the battle against COVID-19. It is also available on Amazon Kindle. Along with this report, we also introduced a database covering additional 1428 artificial intelligence solutions from 12 pandemic scenarios.
本报告介绍了中国在对抗COVID-19的战斗中如何利用人工智能技术。 它也可以在Amazon Kindle上使用 。 除了这份报告，我们还引入了一个 数据库， 涵盖了来自12种大流行情况的其他1428种人工智能解决方案。
Click here to find more reports from us.
单击此处查找我们的更多报告。
We know you don’t want to miss any latest news or research breakthroughs. Subscribe to our popular newsletter Synced Global AI Weekly to get weekly AI updates.
我们知道您不想错过任何最新新闻或研究突破。 订阅我们流行的时事通讯 Synced Global AI Weekly， 以获取每周的AI更新。
翻译自: https://medium.com/syncedreview/a-closer-look-at-the-generalization-gap-in-large-batch-training-of-neural-networks-78aedecac603
神经网络 泛化