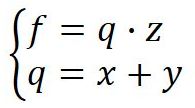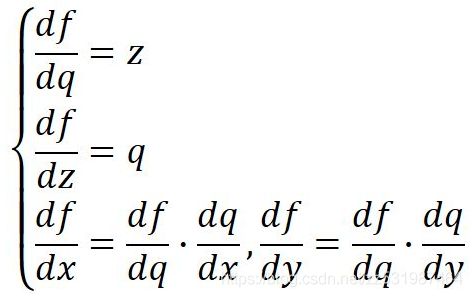卷积神经网络.经典神经网络模型之ResNet

1. 提出ResNet的背景：

一般印象中，越复杂的特征有着越强的表达特征能力。在深度网络中，各个特征会不断的经过线性非线性的综合计算，越深的网络输出表示能力越强的特征。所以网络的深度对于学习表达能力更强的特征至关重要，即神经网络结构越深(复杂，参数多)越是有着更强的表达能力。这一点在VGGNet中得到很好的体现。

深度模型中，每层的输出特征图的尺寸大都随着网络深度而变化，主要是长和宽越来越小，输出特征图的深度随着网络层数的深度而增加。从另一方面讲，长和宽的减小有助于减小计算量，而特征图深度的增加则使每层输出中可用的特征数量增多。

增加深度带来的首个问题就是 梯度爆炸/梯度消失 的问题。这是由于随着层数的增多，在网络中反向传播的梯度会随着连乘变得不稳定，变得特别大或特别小。这其中经常出现的是梯度消失的问题。

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------

补充：什么是梯度消失？

首先回顾一下反向传播的知识

假设我们现在需要计算函数时的梯度，那么首先可以做出如下所示的计算图。

将代入，其中，令，一步步计算，很容易就能得出。

这就是前向传播，即

前向传播是从输入一步步向前计算输出，而反向传播则是从输出反向一点点推出输入的梯度

注：这里的反向传播假设输出端接受之前回传的梯度为1（也可以是输出对输出求导=1）

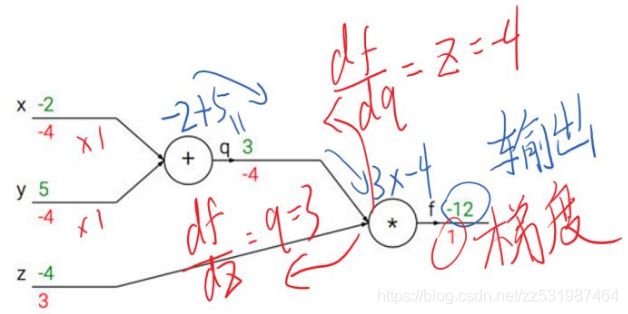
观察上述反向传播，不难发现，在输出端梯度的模值，经过回传扩大了3~4倍。

这是由于反向传播结果的数值大小不止取决于求导的式子，很大程度上也取决于输入的模值。当计算图每次输入的模值都大于1，那么经过很多层回传，梯度将不可避免地呈几何倍数增长（每次都变成3~4倍，重复上万次，想象一下310000有多大……），直到Nan。这就是梯度爆炸现象。

由于至今神经网络都以反向传播为参数更新的基础，所以梯度消失问题听起来很有道理。然而，事实也并非如此，至少不止如此。

我们现在无论用Pytorch还是Tensorflow，都会自然而然地加上Bacth Normalization(简称BN)，而BN的作用本质上也是控制每层输入的模值，因此梯度的爆炸/消失现象理应在很早就被解决了（至少解决了大半）。
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------
恒等映射

Residual Learning的初衷，其实是让模型的内部结构至少有恒等映射的能力。以保证在堆叠网络的过程中，网络至少不会因为继续堆叠而产生退化！

当下Resnet已经代替VGG成为一般计算机视觉领域问题中的基础特征提取网络。

2. 深度残差学习 Deep Residual Learning

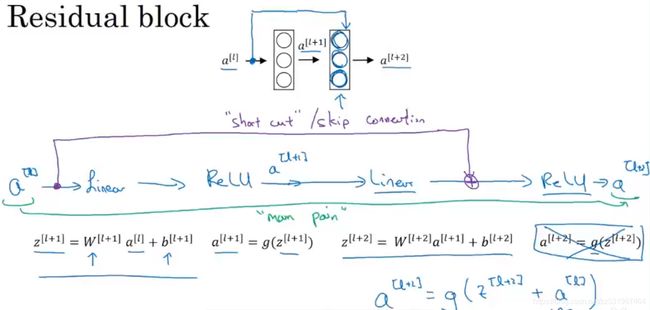
如上图所示：

这里有两层神经网络，开始于，代表第L层中的激活函数，然后是经过一层网络得到，两层后是

由通过线性运算得到(通过乘一个加权矩阵，并加上一个偏置向量)，之后将其应用于非线性ReLU来得到；再下一层，同样应用这个线性步骤以及ReLU变换，得到第二层后的。从流向的信息，它所需要经过的这些步骤，称作主路径main path。

在残差网络中，我们将与之间建立一个快捷路径shot cut(也叫跳跃连接skip connection：指跳过一层或这跳过几乎两层把信息传递到更深的神经网络中去)，所以无需遵循主路径，中的信息现在可以遵循快捷路径进入到更深层的神经网络中。这就意味着 转变为,使到的两层神经网络整体称为一个残差块。

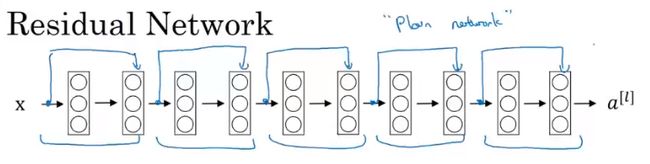
使用残差块可以让你训练更深层的神经网络，而建立一个ResNet的方法就是通过大量的这种残差块，然后把他们堆叠起来，形成一个深层网络。如下所示：

上图显示了5个残差块堆积连接在一起，这就是一个残差网络。

事实证明，如果你使用标准的优化算法，如梯度下降法，以及很高级的优化算法之一来训练普通网络，没有额外的跳跃连接、残差块等，一般从经验上来说，你会发现当你增加层数时，训练误差会在下降一段时间后，会回升上去。在理论上，当你使神经网络更深时，它在训练数据上的性能应该只会更好，一个更深层次的网络只会有帮助。但是实际上，有一个普通网络，没有ResNet，有一个很深的纯网络意味着你的优化算法训练起来会更困难，训练误差会更糟糕。

但是有了ResNet之后，即使层数越来越深，你仍可以让训练误差继续下降，即使我们训练一个超过100层的网络(尽管很少有这么深的网络结构)。将这些激活X或者这些中间层的激活输出，连接到更后面的层去， 这确实对解决梯度消失梯度爆炸问题非常有帮助，使得我们可以训练深得多的神经元网络而不会看到性能倒退的现象。尽管可能在某一点会达到平缓阶段，这时候在加深网络层次也不会有帮助，但是至少不会造成误差上升的情况。

3.ResNet如此有效的原因

一般我们如果设计了更深层的网络，它会使得你用训练集训练神经网络的能力下降，这也是为什么我们不太希望有肽深层的神经网络的原因。但是当训练ResNet的时候就不一样了，具体看下面的例子：

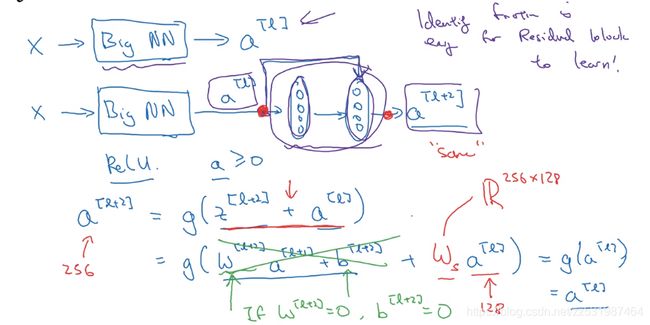
假设你有X作为输入，输入到某个大型神经网络Big NN并输出；如果在这里要调整，使得神经网络层数更深一点，相同的Big NN,然后输出，我们在这后面再增加几层，这里增加两层输出，将连接到间隔一个神经网络中去，形成一个有着跳跃连接的残差块。

在这整个神经网络中我们使用ReLU激活函数，那么所有激活(a)都将会.

由于添加了一个残差块，现在 

这里要注意一下，如果你这里用远离K的L2正则化(regularisation)，这将会减小的值，如果你应用正则化于b的话也会导致b值减小，尽管实际上并不总是需要应用于b，但是这里w才是最需要关注的项。如果为0，同时我们假设也等于0，那么这里所有的项都会消失因为它们都等于0，那么  = =（使用的激活函数为ReLU且我们假设所有激活都不是负数），这意味着残差块比较容易学习恒等函数。由于这个跳跃连接也很容易得到,这意味着将这两层加入到你的神经网络，与上面这个没有这两层的网络相比，并不会非常影响神经网络的能力，因为对它来说学习恒等函数非常容易，只需要复制到，即便它中间有额外两层。所以这就是为什么添加这额外的两层，这个残差块到大型神经网络中间或者尾部并不会影响神经网络的表现。当然我们的目标并不只是维持原有的表现，而是帮助获得更好的表现，可以想象，当这里所有项都学习到有意义的数据时可能要比学习恒等函数更好。残差块网络有效的主要原因是这些额外曾学习起恒等函数非常简单，你几乎总能保证它不会影响总体的表现，甚至很多时候幸运的话还可以提升网络的表现，至少有个合理的底线，不会影响其表现，然后梯度下降从这里开始可以改善最终的结果。

残差网络的另一个值得讨论的细节是，我们是在假定和在同一维度的，所以你将会看到在ResNet中许多相同卷积的应用，所以在残差块的两个连接点的维度与输出层的维度相同，这样也会使得运算变得相对方便，然后运算这个两个相同维度矢量的和。如果输入和输出有不同的维度，那么我们需要添加一个使得最终的维度相同，它可以是一个包含已学习到的参数的矩阵，也可以是一个固定的矩阵，其中包含很多0的项，即除了以外，由0来填满256维。这也是一种保证维度相同的方法(增加一个的矩阵来保证维度相同/使用same conv保证输入输出维度相同，这样在跳跃连接后的计算能够正常进行，毕竟只有同维度的矩阵才可以做加法)

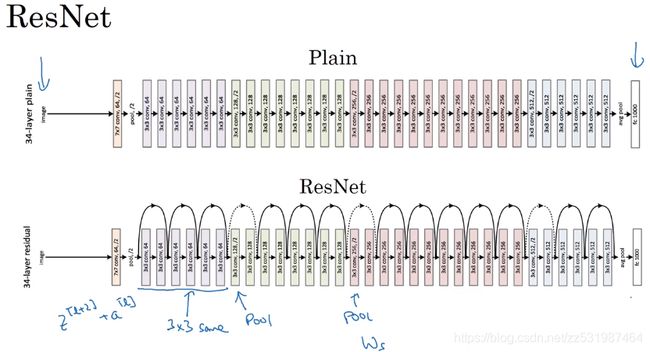
4. ResNet

ResNet使用了很多的same conv，保证输入和输出的维度相同，这样在跳跃连接后，维度相同，相加的算数得以成立。但是有时候中间神经单元经过线性计算后会经过池化层改变了维度，那么我们可以使用的矩阵保证维度相同。

 

参考博文如下：

Resnet到底在解决一个什么问题呢？

深度学习网络篇——ResNet

经典分类CNN模型系列其四：Resnet