Scikit-Learn机器学习（knn算法）

前言

博观而约取，厚积而薄发

本文中回忆了python的类概念，机器学习需要用到的环境，以及什么是Scikit-Learn 目的是方便博主进行回忆 记忆学习 和总结 如果能帮助到大家 那就更好了

Python类中的 私有变量和私有方法

默认情况下，Python中的成员函数和成员变量都是公开的(public),在python中没有类似public,private等关键词来修饰成员函数和成员变量。
在python中定义私有变量只需要在变量名或函数名前加上 ”__“两个下划线，那么这个函数或变量就是私有的了。
在内部，python使用一种 name mangling 技术，将 __membername替换成 _classname__membername，也就是说，类的内部定义中,
所有以双下划线开始的名字都被"翻译"成前面加上单下划线和类名的形式。
例如：为了保证不能在class之外访问私有变量，Python会在类的内部自动的把我们定义的__spam私有变量的名字替换成为
_classname__spam(注意，classname前面是一个下划线，spam前是两个下划线)，因此，用户在外部访问__spam的时候就会
提示找不到相应的变量。 python中的私有变量和私有方法仍然是可以访问的；访问方法如下：
私有变量:实例._类名__变量名
私有方法:实例._类名__方法名()

其实，Python并没有真正的私有化支持，但可用下划线得到伪私有。 尽量避免定义以下划线开头的变量！
（1）_xxx "单下划线 " 开始的成员变量叫做保护变量，意思是只有类实例和子类实例能访问到这些变量，
需通过类提供的接口进行访问；不能用’from module import *'导入
（2）__xxx 类中的私有变量/方法名 （Python的函数也是对象，所以成员方法称为成员变量也行得通。）,
" 双下划线 " 开始的是私有成员，意思是只有类对象自己能访问，连子类对象也不能访问到这个数据。
（3）xxx 系统定义名字，前后均有一个“双下划线” 代表python里特殊方法专用的标识，如 init（）代表类的构造函数。

【Python 必会技巧】[i for i in range(1,10)] — 列表解析式，列表中使用 for 循环

经常会看到类似于 [i for i in range(1,10)] 的表达式，这种表达式称为列表解析（List Comprehensions），类似的还有字典解析、集合解析等等。

列表解析式是将一个列表（实际上适用于任何可迭代对象）转换成另一个列表的工具。在转换过程中，可以指定元素必须符合一定的条件，才能添加至新的列表中，这样每个元素都可以按需要进行转换。

每个列表解析式都可以重写为 for 循环，但不是每个 for 循环都能重写为列表解析式，列表解析比 for 更精简，运行更快。

基本语法
[expression for iter_val in iterable]

[expression for iter_val in iterable if cond_expr]

用 for 循环实现如下：

>>> li = []
>>> for i in range(1, 11):
	li.append(i*2)

>>> print(li)
[2, 4, 6, 8, 10, 12, 14, 16, 18, 20]

用列表解析式实现如下：

>>> li = [i*2 for i in range(1, 11)]
>>> print(li)
[2, 4, 6, 8, 10, 12, 14, 16, 18, 20]

python中的类

类去封装函数和变量 类最基本的作用就是在封装代码

类的方法与普通的函数只有一个特别的区别——它们必须有一个额外的第一个参数名称，但是在调用这个方法的时候你不为这个参数赋值，Python会提供这个值。这个特别的变量指对象本身，按照惯例它的名称是self。

1. python中的类中的第一个特性就是其中的方法要加self 要不就会报错
2. 类中的方法使用全局变量的时候一定要加上self.变量名称 要不也会报错
3. 函数的调用一定要在实例化之后再调用对象中的方法
4. 类只是去刻画一些东西 去描述了学生的名称和年龄 定义了一个行为，但是他不会去执行代码
5. 类的最基本就是封装，所以类的调用是不可以调用的

#类去封装函数和变量 类最基本的作用就是在封装代码

class Student():
    name=''
    age=0

    def print_file(self):
        print('name:'+ self.name)
        print('age:'+ str(self.age))


class StudentHomeWork():
    homwwork_name=''

student = Student()
student.print_file()

构造函数（方法）

我们在类定义好 再对对象进行实例化的时候，如果我们定义三个学生，那么这三个学生所被刻画的特征和行为岂不是一样？
那么我不想让他们一样 想改变下，该如何改变，我们需要构造一个特殊的方法我们来看下 也就是构造函数（构造方法）
def init(self):

1. 构造函数的调用是自动进行的
2. 构造函数返回值不能是字符串 而其他函数可以return返回值
3. 构造函数的作用 是让模板生成不同的对象
4. 在构造函数的里面增加不同的参数，我们就可以在实例化的时候进行传入不同的值，让对象变得不同，丰富起来

#类去封装函数和变量 类最基本的作用就是在封装代码


#类去封装函数和变量 类最基本的作用就是在封装代码

class Student():
    #类变量的意义在哪里
    sum = 0
    c=50

    def add(self,x,y):
        c = x+y #普通方法中的局部变量
        # self.c = x+y
        # print(self.c) #这里就会修改全局变量的值
        print(c) #局部变量的c

    #类变量 实例变量
    def __init__(self,name,age):
        #构造函数 初始化对象属性
        #使用self.name 保存内部的特征值 self.name 就是实例变量
        self.name = name
        self.age = age
        #这里注意如果是不加self的话 局部变量是不会覆盖全局变量的
        #print('student')


    def print_file(self):
        print('name:'+ self.name)
        print('age:'+ str(self.age))
        return 'student'



student1 = Student('python',20)
student2 = Student('java',12)
print(student1.name)
print(student2.name)
student1.add(3, 1)
print(student1.c) #全局变量的c
# student1= Student()
# student2 = Student()
# a= student.print_file()
# print(a)

self不能称作是关键字 关键字是固定不变的 self可以改变 可以改成this 任何词语 python推荐self

类变量和实例变量

类变量的作用在何处呢？
我们可以在类中定义一个sum = 0
类变量是和对象无关的 是通过类名可以直接调用
实例对象需要加上self。变量名称 可以在实例化中的对象中调用

print(student1.dict)
{‘name’: ‘python’, ‘age’: 20}
可以打印对象中的所有实例变量

构造函数和实例方法构造的方式不一样的 构造函数是通过类的参数调用
实例方法是通过 实例化后的对象 传入参数调用的
实例方法用于描述类的行为
构造函数的为了初始化类的各种特征和行为的

print(self.class.sum1)
print(Student.sum1)
在方法中调用类方法的两种方式

Scikit-Learn机器学习

我们补习了python一部分基础后，现在来看下Scikit-Learn是什么，之前其实就了解过这个但是博主并不是很细心，今天收到一个博主的影响决定再次开始尝试一步一步把实验做完做下去

我们在进入Scikit-learn之前需要有些准备工作 第一步环境 ipython 第二步所需要的一些python中强大的工具 numpy基础 以及 Matplotlib数据可视化基础
可以看我的之前博客

什么是scikit-learn？？？

scikit-learn工具包包含了几乎所有主流的机器学习算法

Scikit-learn（以前称为scikits.learn，也称为sklearn）是针对Python 编程语言的免费软件机器学习库 [1] 。它具有各种分类，回归和聚类算法，包括支持向量机，随机森林，梯度提升，k均值和DBSCAN，并且旨在与Python数值科学库NumPy和SciPy联合使用。
-----来自 百度百科

机器学习的八大算法

1. k近邻算法
2. 线性回归算法
3. 逻辑回归算法
4. 决策树
5. 支持向量机（手写识别算法model）
6. 朴素贝叶斯算法
7. pca算法
8. k均值算法

我们先从最简单的knn算法开始走入机器学习的世界

KNN算法

中国有一句话 近朱者赤近墨者黑 k近邻就是这样

我们来看这里有一部分数据 ，然后再引入一个数据 设置k的值 如果附近都是蓝色那他有很大的概率是同一类别

先导入癌症数据
x，和y 然后转化成numpy数组

raw_data_X=[[3.393533211,2.3312733811],
           [3.110073483,1.781539638],
           [1.343808831,3.368360954],
           [3.582294042,4.679179110],
           [2.280362439,2.866990263],
           [7.423436942,4.696522875],
            [5.745051997,3.533989803],
            [9.17216865,2.511101045],
            [7.792783481,3.4240889411],
            [7.939820817,0.7916372311]]

raw_data_y=[0,0,0,0,0,1,1,1,1,1]

设置训练集

X_train = np.array(raw_data_X)
y_train = np.array(raw_data_y)
//绘图
plt.scatter(X_train[y_train==0,0],X_train[y_train==0,1],color='g')
plt.scatter(X_train[y_train==1,0],X_train[y_train==1,1],color='r')

如果这里新增一组数据

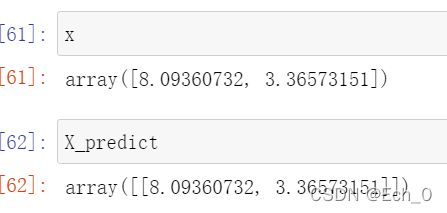
x=np.array([8.093607318,3.365731514])

plt.scatter(X_train[y_train==0,0],X_train[y_train==0,1],color='g')
plt.scatter(X_train[y_train==1,0],X_train[y_train==1,1],color='r')
plt.scatter(x[0],x[1],color='b')

我们可以看到 x在红色的区间内

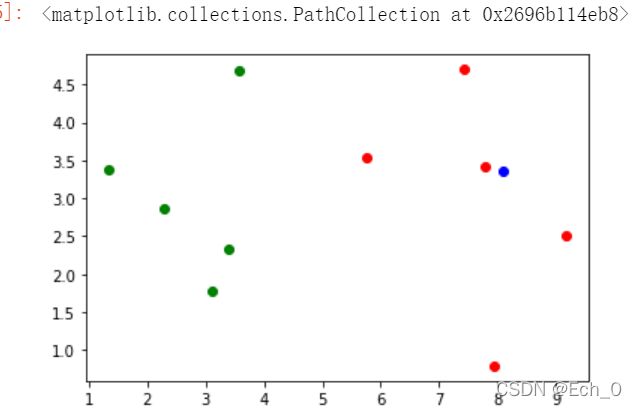
我们来看下knn的过程 要进行x和其他点的过程

第一步我们要计算每个点直接的距离 这里就需要用到了欧拉距离
从初中的坐标点 然后升级到三维 到多维 的小下标然后简化

我们可以设置一个for循环来看距离

from math import sqrt
distances = []
for x_train in X_train:
    d = sqrt(np.sum((x_train - x)**2))
    distances.append(d)
distances

out put 为
[4.812566907588383,
5.229270827235305,
6.749798999160064,
4.6986266144110695,
5.83460014556857,
1.4900114024329525,
2.354574897431513,
1.3761132894601276,
0.3064319993165442,
2.5786840956480668]

也可以简化用一行写出来

distances = [sqrt(np.sum((x_train - x)**2)) for x_train in X_train]

然后在用np.argsort(distances)进行排序返回索引值

np.argsort(distances)

array([8, 7, 5, 6, 9, 3, 0, 1, 4, 2], dtype=int64)

然后我们拿这个索引值 带入y_train中拿到所对用的特征是良性还是恶性

k_nearest = np.argsort(distances)
k=6
topK_y=[y_train[i] for i in k_nearest[:k]]
topK_y
from collections import Counter
Counter(topK_y)
//使用cuonter中的votes方法投票
votes = Counter(topK_y)
votes.most_common(1)
//最终预测结果
votes.most_common(1)[0][0]
predict_y = votes.most_common(1)[0][0]
predict_y

output 1

scikit learn 机器学习算法封装方法

我们可以把以上的内容 都写在一个模块中 然后从jupyter中导入这个模块，于是就可以进行传入参数直接得到判断结果。


这就是简单使用函数的方式把算法封装起来了，然后我们再来回顾下 什么是机器学习？
这就是机器学习的基本流程，那么knn算法并没有得到什么模型啊，确实如此，knn是唯一一个不需要训练模型，直接可以投票得出的机器学习算法

但是其实训练数据集本身，就是模型本身。

机器学习算法，就是把数据集拷贝过来 训练（fit拟合）成模型，训练集本身就是模型，然后预测出结果。
只不过对于knn算法来说这种过程是很简单的

scikit-learn中的knn

首先第一步也是要引入这个模块，在scikit-learn中是以对象的方式，所以我们也需要实例化一下 sklearn中KNeighborsClassifier包装了knn算法

from sklearn.neighbors import KNeighborsClassifier
#KNeighborsClassifier包装了一个算法 而且是以面向对象的方式
实例化
KNN_classifier = KNeighborsClassifier(n_neighbors=6)
传入参数就是k的值是6
#模型存在实例中的  fit方法进行拟合数据
KNN_classifier.fit(X_train,y_train)
//然后就拟合好了模型 我们接下来进行预测
x=np.array([8.093607318,3.365731514])
X_predict = x.reshape(1,-1)
预测
y_predict = KNN_classifier.predict(X_predict)

实例化后使用实例中的fit进行拟合 得到模型然后我们就可以进行预测了
调用KNN_classifier.predict方法
y_predict = KNN_classifier.predict(X_predict)
y_predict output：array([1])
得到预测结果是1和上面我们手写的knn结果一致

这里需要注意的是如果直接把x的值传入就会报错，因为你要预测的话需要把数组转换成矩阵的形式，多个的话就多个矩阵，一个的话也得转换成矩阵，方法就是reshape（1，-1）后面的-1是为了让系统自己去分配有几行

y_predict = KNN_classifier.predict(x)

reshape之前x是数组，之后是两个方括号的矩阵

数组与矩阵的区别
矩阵中的元素只能是数字，而数组中的元素可以是字符或者字符串
矩阵是二维的，数组可以是一维的、多维的
矩阵显示时，元素之间无逗号；数组显示时，元素之间用逗号隔开

矩阵是数组的特殊形式

---

这是非常简单的使用scikit-learn中的封装好的机器学习的算法进行预测的一个过程，我们整理下，我们相应的机器学习对应的算法，然后创建算法所对应的实例，如果算法需要一些参数，我们也需要传入参数，然后需要拟合fit训练数据集，然后就可以predict 的预测过程了

sklearn标准流程：

1. 导入对应算法模块
2. 创建算法实例 传入参数
3. 拟合训练数据集
4. 进行预测

这是个很标准的流程，在sklearn中所有的机器学习算法都是这个流程

那么我们可以来模拟写一个同样的算法：



当然sklearn中的封装的比我们的要复杂一些，我们也可以自己封装达到同样的效果，那么我们有个问题 到底我们这个预测的正确率如何呢？？我们怎么判断呢

判断机器学习算法的性能

其实就是把数据集划分为训练集和测试集 通常是8：2或者7：3

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

我们要是直接分的话是很不平均的，y的结果前100不包括种类为2的鸢尾花。
那我们就需要对原始的数据进行乱序处理。

有两种方法，一个是把X与y进行拼接得到（150，5）的矩阵然后打乱顺序后再分成（150，4）的矩阵

这里可以使用另外一种方式，我们只需要把对应的索引进行乱序处理

shuffle_indexes = np.random.permutation(len(X))
test_ratio= 0.2
test_size = int(len(X)* test_ratio)
test_indexes = shuffle_indexes[:test_size]
train_indexes = shuffle_indexes[test_size:]

X_train = X[train_indexes]
y_train = y[train_indexes]

X_test = X[test_indexes]
y_test = y[test_indexes]

KNN_classifier = KNeighborsClassifier(n_neighbors=6)
KNN_classifier.fit(X_train,y_train)
y_predict = KNN_classifier.predict(X_test)
y_predict
sum(y_predict==y_test)
sum(y_predict==y_test)/len(y_test)

分类的准确性

先引入sklearn中的分割模块，把数据集进行分割处理

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)

第二步引入sklearn中的knn分类模块 设置参数进行模型拟合

from sklearn.neighbors import KNeighborsClassifier
KNN_classifier = KNeighborsClassifier(n_neighbors=3)
KNN_classifier.fit(X_train,y_train)

第三步使用模型进行预测 同时引入评分模块 查看模型的预测结果的好坏

y_predict = KNN_classifier.predict(X_test)
from sklearn.metrics import accuracy_score
accuracy_score(y_test,y_predict)

也可以用模型中自带的方法查看模型的预测准确率（不看预测结果的情况）

KNN_classifier.score(X_test,y_test)

超参数

那么我们在设置knn算法的时候 究竟需要传入什么参数最好呢？？

超参数：在算法运行前需要决定的参数
模型参数：算法过程中学习的参数

knn没用模型参数
knn中的k是典型的超参数

我们来寻找最好的k

best_score = 0.0
best_k= -1
for k in range(1,11):
    knn_clf= KNeighborsClassifier(n_neighbors=k)
    knn_clf.fit(X_train,y_train)
    score = knn_clf.score(X_test,y_test)
    if score >best_score:
        best_k = k
        best_score = score
print("best_k:",best_k)
print("best_score:",best_score)

best_k: 3
best_score: 0.9916666666666667

引入另外一个超参数，就是距离

best_method=""
best_score = 0.0
best_k= -1
for method in ["uniform","distance"]:
    for k in range(1,11):
        knn_clf= KNeighborsClassifier(n_neighbors=k,weights=method)
        knn_clf.fit(X_train,y_train)
        score = knn_clf.score(X_test,y_test)
        if score >best_score:
            best_k = k
            best_score = score
            best_method = method
print("best_method:",best_method)      
print("best_k:",best_k)
print("best_score:",best_score)

我们来看一些距离的公式

1. 曼哈顿距离
2. 欧拉距离
3. 明可夫斯基距离
   

%%time

best_p=-1
best_score = 0.0
best_k= -1
for k in range(1,11):
    for p in range(1,6):
        knn_clf= KNeighborsClassifier(n_neighbors=k,weights="distance",p=p)
        knn_clf.fit(X_train,y_train)
        score = knn_clf.score(X_test,y_test)
        if score >best_score:
            best_k = k
            best_score = score
            best_p = p
print("best_k:",best_k)
print("best_score:",best_score)
print("best_p:",best_p)

best_k: 3
best_score: 0.9916666666666667
best_p: 2
Wall time: 27.9 s

这里就是欧拉距离时候是最好的

网格搜索与k近邻算法中更多的超参数

网格搜索法是指定参数值的一种穷举搜索方法，通过将估计函数的参数通过交叉验证的方法进行优化来得到最优的学习算法。

即，将各个参数可能的取值进行排列组合，列出所有可能的组合结果生成“网格”。然后将各组合用于SVM训练，并使用交叉验证对表现进行评估。在拟合函数尝试了所有的参数组合后，返回一个合适的分类器，自动调整至最佳参数组合，可以通过clf.best_params_获得参数值

我们这里调用sklearn自带的方法

param_grid=[
    {
        'weights':['uniform'],
        'n_neighbors':[i for i in range(1,11)]
    },
    {
        'weights':['distance'],
        'n_neighbors':[i for i in range(1,11)],
         'p':[i for i in range(1,6)]
    }
]

knn_clf = KNeighborsClassifier()
from sklearn.model_selection import GridSearchCV

grid_search = GridSearchCV(knn_clf,param_grid)
%%time
grid_search.fit(X_train,y_train)
grid_search.best_estimator_

//n_jobs所有核进行网格搜索
grid_search = GridSearchCV(knn_clf,param_grid,n_jobs=-1)
//有一些输出看现在搜索状态 不同的值对应的搜索信息不同
grid_search = GridSearchCV(knn_clf,param_grid,n_jobs=-1，verbose=2)

更多距离定义：
（数学很重要）
相似度去定义距离

数据归一化 Scaler

为什么要数据归一化？？？
将数据映射到统一尺度中
最值归一化，把所有数据映射到0-1直接

“数据归一化处理的目的是：使得预处理的数据被限定在一定的范围内，从而消除奇异样本数据导致的不良影响。数据归一化处理后，可以加快梯度下降求最优解的速度，且有可能提高精度（如KNN）。

1. 最值归一化normalization 适用于分布有明显边界的情况（考试分数 图像像素），受outlier影响较大
2. 均值方差归一化standardization 把数据归一到均值为0方差为1的分布中 适用于数据分布没明显分布 （收入分布，一般都使用均值方差归一化）有可能存在极端数据值
   

scikit-learn中封装的归一化方法

测试数据是模拟真实环境，真实环境又无法得到所有测试数据的均值和方差，所以在对数据归一化的时候需要注意有些不同。对数据归一化也是算法的一部分。
我们要保存数据集划分的训练集中的 方差和平均值
在scikit-learn中使用Scaler，其实fit训练的时候步骤是一致的 只不过是一步数据的处理，使数据更加的准确

其实也就是数据的预处理

#数据的预处理
from sklearn.preprocessing import StandardScaler
standScaler= StandardScaler()
standScaler.fit(X_train)
#mean_ 不是用户传进去的变量 是用户计算出来的变量可以随时从外部进行查询
standScaler.mean_
standScaler.scale_
//归一化处理
standScaler.transform(X_train)

这样数据就进行归一化处理了，但是我们的X_tran并没有改变 我们需要设置接收一下

X_train_standard = standScaler.transform(X_train)
X_test_standard = standScaler.transform(X_test)

我们使用归一化的数据进行归一化分类

from sklearn.neighbors import KNeighborsClassifier
knn_clf =KNeighborsClassifier(n_neighbors=3)
knn_clf.fit(X_train_standard,y_train)
knn_clf.score(X_test_standard,y_test)

就是我们训练集归一化后，测试集也必须归一化！！！

关于k近邻算法 最基本机器学习算法

k近邻算法解决分类问题，思想简单，效果强大，也可以解决回归问题，回归问题就是返回一个数值，下一个时刻房价是多少？？
用到的是kneighborsRegressor
最大的缺点：效率低下，训练m个样本n个特性预测新数据就是需要时间复杂度O(m*n)
就算引入树结构也是效率很低
缺点2：高度数据相关
缺点3：预测结果不具有可解释性

随着维度增加，看似很近的两个点之间的距离会越来越大

机器学习流程回顾

如何使用机器学习算法，这些流程上的步骤是更加重要的！！！
knn分类算法结束，下一篇学习回归问题！！！