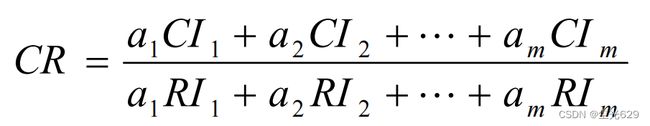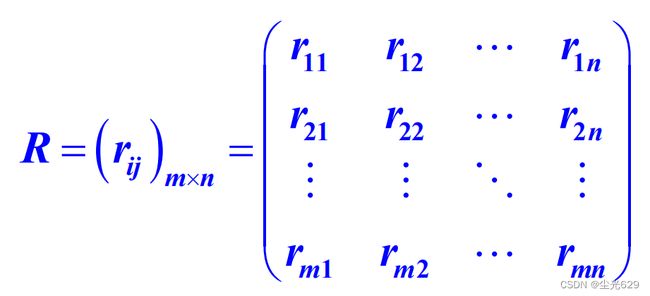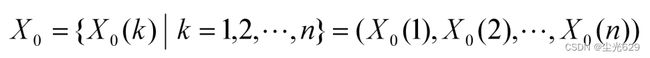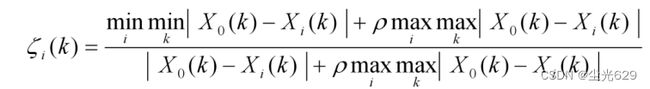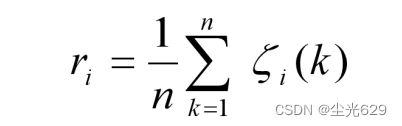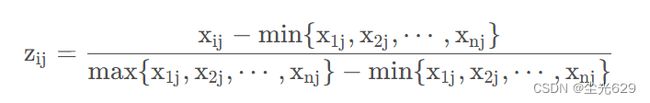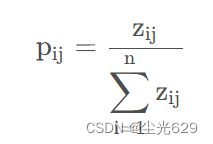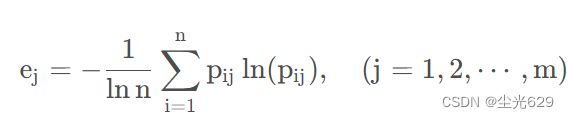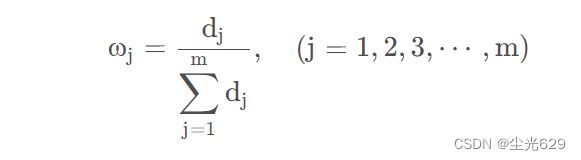评价类问题解决方法及模型汇总
- 评价类问题的基本范畴
- 对题中所给目标按照一定的标准进行分类
- 将题中数据运用数学模型进行处理,并得到唯一指标结果进行比较或排序
- 探究某一综合问题的不同方面并计算验证其总体实现程度
- 评价类问题的基本要素
- 被评价对象 如(工厂产品、员工绩效)
- 评价指标 如(生产成本、运输损耗)
- 权重系数 如(原料价格优先级高,维护费用优先度低)
- 评价模型 如(灰色模型、模糊综合)
- 评价主体 如(商场经理、上游经销商)
- 评价类问题的主要步骤
- 明确评价问题目的
- 建立评价指标体系
- 对数据进行预处理
- 判断评价指标权重
- 计算综合评价总值
四、评价类问题的模型分类
这里简要说明几种常用的方法:
(1)主成分分析法
释义:
主成分的概念由Karl Pearson在1901年提出的。他是考察多个变量间相关性一种多元统计方法研究如何通过少数几个主成分来解释多个变量间的内部结构。即从原始变量中导出少数几个主分量,使它们尽可能多地保留原始变量的信息,且彼此间互不相关。建立主成分分析的目的:数据的压缩或数据的解释
具体步骤:
1 对原来的p个指标进行标准化,以消除变量在水平和量纲上的影响
2 根据标准化后的数据矩阵求出相关系数矩阵
3 求出协方差矩阵的特征根和特征向量
4 确定主成分,并对各主成分所包含的信息给予适当的解释
数学模型:
假定有n个地理样本,每个样本共有p个变量,构成一个n×p
阶的地理数据阵
当p较大时,在p维空间中考察问题比较麻烦。为了克服这一困难,
就需要进行降维处理,即用较少的几个综合变量代替原来较多的
变量变量,而且使这些较少的综合变量能尽量多地反映原来较
多变量所反映的信息。以下是降维所需具体公式:
求取方差尽可能大的线性函数
模型检验:
如果多个变量相互独立或相关性很小,就不能进行主成分分析。
KMO检验:检验变量之间的偏相关系数是否过小。
Bartlett’s 检验。该检验的原假设是相关矩阵为单位阵(不相
关),如果不能拒绝原假设,则不适合进行主成分分析。
补充说明:
主成分就是以协方差阵的特征向量为系数的线性组合,它们互不相关,其方差即为矩阵的特征根,主成分的名次是按特征根取值大小的顺利排列的。
往年例题:
2005年A题《长江水质的评价和预测》
2012年A题《葡萄酒的评价》
(2)层次分析法
释义:
层次分析法(AHP)是美国运筹学家匹茨堡大学教授萨蒂(T.L.Saaty)于上世纪70年代初,为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”课题时,应用网络系统理论和多目标综合评价方法,提出的一种层次权重决策分析方法。
这种方法的特点是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上,利用较少的定量信息使决策的思维过程数学化,从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法,是对难于完全定量的复杂系统作出决策的模型和方法。
具体步骤:
1 建立层次结构模型
2 构建判断矩阵
3 层次单排序及一致性检验
4 层次多排序及一致性检验
数学模型:
判断矩阵的构建原则
构建结果如图所示
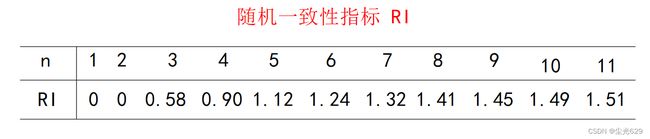
层次排序
一致性检验
CI=λ-n/n-1
模型检验:
CR<0.1时,认为不一致程度在容许范围之内,有满意的一致性,即通过一致性检验。可用其归一化特征向量作为权向量,否则要重新构
造成对比较矩阵A,再做评判。
补充说明:
层次分析法存在粗略、主观等局限性.首先是它的比较、判断及结果都是粗糙的,不适于精度要求很高的问题;其次是从建立层次结构图到给出两两比较矩阵,人的主观因素作用很大,使决策结果较大程度地依赖于决策人的主观意志,可能难以广泛接受。
往年例题:
2002年B题《彩票中的数学》
2006年B题《艾滋病疗法的评价及疗效的预测》
2010年B题《2010年上海世博会影响力的定量评估》
(3)模糊综合评价法
释义:
模糊综合评价作为模糊数学的一种具体应用,最早由我国学者汪培庄提出。基本思想是:以模糊数学为基础,应用模糊关系合成原理,将一些边界不清、不易定量的因素定量化,从多个因素对被评价事物隶属等级状况进行综合评价。具体步骤为:首先确定被评价对象的因素集和评价集,然后再分别确定各因素的权重及它们的隶属度向量,获得模糊评价矩阵,最后将模糊评价矩阵与因素的权向量进行模糊运算并归一化,从而得到模糊评价综合结果。
具体步骤:
1 确定因素集
2 确定评语集
3 确定各因素的权重
4 确定模糊综合判断矩阵
5 综合评判
数学模型:
模糊集和评语集
U={u1,u2,……,un}
V={v1,v2,……,vm}
权重向量
A=[a1,a2,……,an]
∑ai=1 i=1,2,……,n
模糊综合判断矩阵
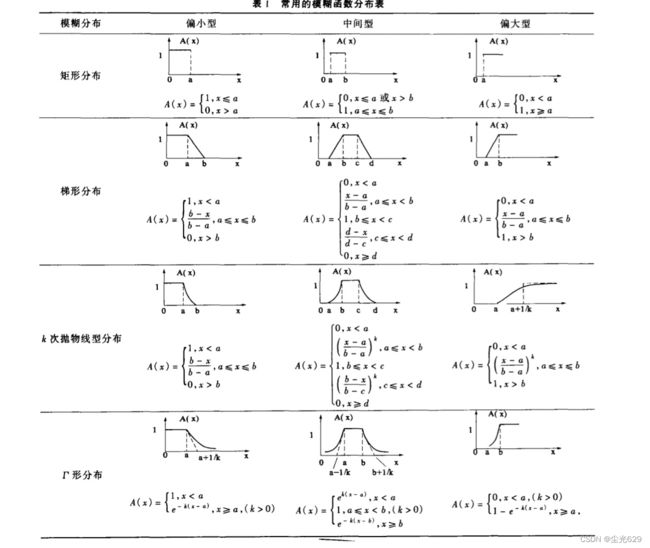
求取隶属度
综合评判 W=A·R
模型检验:
可以与灰色模型或聚类算法连用,套用其检验方式
补充说明:
模糊综合评判法的计算较为复杂,对指标权重矢量的确定主观性较强。当指标集U较大,即指标集个数凡较大时,在权矢量和为1的条件约束下,相对隶属度权系数往往偏小,权矢量与模糊矩阵R不匹配,结果会出现超模糊现象,分辨率很差,无法区分谁的隶属度更高,甚至会造成评判失败。
往年例题:
2002年B题《彩票中的数学》
2010年B题《2010年上海世博会影响力的定量评估》
2012年A题《葡萄酒的评价》
(4)灰色关联分析法
释义:
灰色系统理论(Grey System Theory)诞生于20世纪80年代。邓聚龙教授在1981年上海中-美控制系统学术会议上所作的“含未知数系统的控制问题”的学术报告中首次使用了“灰色系统”一词,是指部分信息已知,部分信息未知的“小样本,贫信息”不确定性系统,即信息不完全的系统。灰色系统理论主要通过对“部分”已知信息的挖掘、开发,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控。
具体步骤:
1 确定比较数列和参考数列
2 确定各指标对应的权重
3 计算灰色关联系数
4 计算灰色加权关联度
5 评价分析
数学模型:
评价指标体系的构建
参考数列的构建
灰色关联系数与灰色加权关联度
0<ρ<1
如果{X0 (k) }为最优值数据列,ξ(k)越大,越好;
如果{X0 (k) }为最劣值数据列,ξ(k)越大,越不好
模型检验:
补充说明:
灰色关联分析法要求需要对各项指标的最优值进行现行确定,主观性过强,同时部分指标最优值难以确定。
往年例题:
2006年B题《艾滋病疗法的评价及疗效的预测》
2013年B题《碎纸片的拼接复原》
(5)熵权法
释义:
熵权法,按照信息论基本原理的解释,信息是系统有序程度的一个度量,熵是系统无序程度的一个度量;根据信息熵的定义,对于某项指标,可以用熵值来判断某个指标的离散程度,其信息熵值越小,指标的离散程度越大, 该指标对综合评价的影响(即权重)就越大,如果某项指标的值全部相等,则该指标在综合评价中不起作用。因此,可利用信息熵这个工具,计算出各个指标的权重,为多指标综合评价提供依据。
基本步骤:
1 利用原始数据矩阵计算评价第i个对象关于第j个指标值的权重
2 计算第j项指标的熵值
3 计算第j项指标的变异系数
4 计算第j项指标的权重
5 计算第i个评价对象的综合评价值
数学模型:
求取比重数值
求取熵值
求取熵权
模型检验:
套用一致性检验或其他相关性检验参数
补充说明:
熵权法忽略了指标本身重要程度,有时确定的指标权数会与预期的结果相差甚远,同时熵权法不能减少评价指标的维数,换而言之,熵权法符合数学规律具有严格的数学意义,但往往会忽视决策者主观的意图。
往年例题:
2002年B题《彩票中的数学》
2016年B题《小区开放对道路通行的影响》