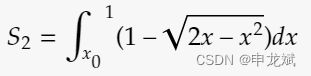详解欧拉计划之第587题：凹三角形

欧拉计划第587题：

不妨假设圆的半径为1。

第一步，先计算出L形截面的面积

L形截面相当于正方形里抠掉1/4个圆。

$S_0=1-\frac{\pi }{4}$

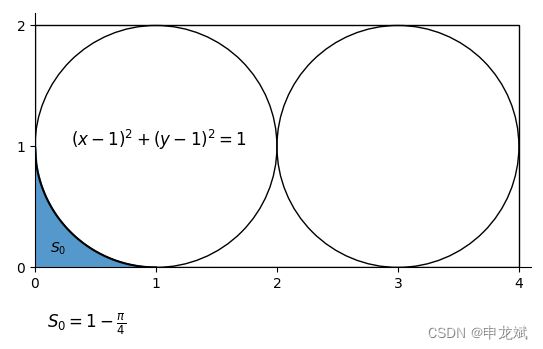
画上面的这个图，用到了matplotlib的python代码，也一并贴出来供参考。

import numpy as np
import matplotlib.pyplot as plt

fig, ax = plt.subplots()

# 保持纵横比，这样圆不会画成一个椭圆
ax.set_aspect('equal')

# 不显示上面和右面的边框线
ax.spines[['top', 'right']].set_visible(False)

# 画2个圆
circle1 = plt.Circle((1, 1), 1, edgecolor='black', fill=False)
ax.add_patch(circle1)
circle2 = plt.Circle((3, 1), 1, edgecolor='black', fill=False)
ax.add_patch(circle2)

# 画包围2个圆的矩形
ax.add_patch(plt.Rectangle((0, 0), 4, 2, edgecolor='black', fill=False))

# 左下角L形区域
x = np.linspace(0, 1, 100)
y = 1 - np.sqrt(2*x - x*x)
ax.plot(x, y, color='black')
ax.fill_between(x, y, color='#5599cc')

ax.text(0.12, 0.12, r'$S_0$')
ax.text(0.1, -0.5, r'$S_0=1 - \frac{\pi}{4}$', size='12')
ax.text(0.3, 1, r'$(x-1)^2+(y-1)^2=1$', size='12')

#ax.plot([0, 4], [0, 2], 'black', linewidth=1)
ax.set_xlim(0, 4.1)
ax.set_xticks(range(0, 5))
ax.set_ylim(0, 2.1)
ax.set_yticks(range(0, 3))

fig.show()

第二步，计算凹三角形的面积

设n为圆的个数，当n=2时，用matplotlib绘出来的图，凹三角形如下所示。

相应的python绘图代码：

import numpy as np
import matplotlib.pyplot as plt

fig, ax = plt.subplots()

# 保持纵横比，这样圆不会画成一个椭圆
ax.set_aspect('equal')

# 不显示上面和右面的边框线
ax.spines[['top', 'right']].set_visible(False)

# 画2个圆
circle1 = plt.Circle((1, 1), 1, edgecolor='black', fill=False)
ax.add_patch(circle1)
circle2 = plt.Circle((3, 1), 1, edgecolor='black', fill=False)
ax.add_patch(circle2)

# 画包围2个圆的矩形
ax.add_patch(plt.Rectangle((0, 0), 4, 2, edgecolor='black', fill=False))

# 左下角凹三角形区域，分2部分画出
x = np.linspace(0, 0.4, 100)
y = 0.5 * x
ax.plot(x, y, color='black')
ax.fill_between(x, y, color='r')

x = np.linspace(0.4, 1, 100)
y = 1 - np.sqrt(2 * x - x * x)
ax.plot(x, y, color='black')
ax.fill_between(x, y, color='r')

# 画(0, 0) 到 右上角的连线
ax.plot([0, 4], [0, 2], 'black', linewidth=1)

ax.set_xlim(0, 4.1)
ax.set_xticks(range(0, 5))
ax.set_ylim(0, 2.1)
ax.set_yticks(range(0, 3))

fig.show()

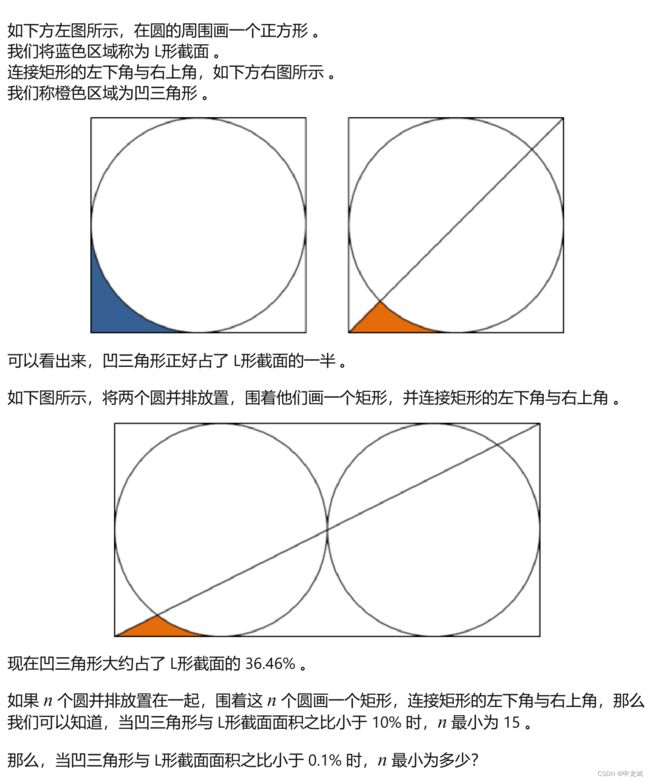
把凹三角形那个图像放大一些仔细研究，可以看出它有2部分组成，左侧是一个直角三角形，右侧是一段圆弧与x轴围出的一块区域，直线和曲线的方程用到一点点解析几何的知识，如下图。

相应的python绘图代码：

import numpy as np
import matplotlib.pyplot as plt

fig, ax = plt.subplots()

# 保持纵横比，这样圆不会画成一个椭圆
ax.set_aspect('equal')

# 不显示上面和右面的边框线
ax.spines[['left',  'top', 'right']].set_visible(False)

# 左下角凹三角形区域，分2部分S1、S2画出
x = np.linspace(0, 0.4, 100)
y = 0.5 * x
ax.plot(x, y, color='black')
ax.fill_between(x, y, color='#FF8800')

ax.text(0.25, 0.05, r'$S_1$')
ax.text(0.1, 0.1, r'$y = \frac{1}{n} x$', rotation=26.5)

x = np.linspace(0.4, 1, 100)
y = 1 - np.sqrt(2 * x - x * x)
ax.plot(x, y, color='black')
ax.fill_between(x, y, color='#FF0033')

ax.text(0.5, 0.05, r'$S_2$')
ax.text(0.6, 0.05, r'$y = 1 - \sqrt{2x - x^2}$', rotation=-25)

ax.text(0.35, 0.22, r'$(x_0, y_0)$')

ax.set_xlim(0, 1)
ax.set_xticks([0, 1])
ax.set_yticks([])

fig.show()

凹三角形的面积等于S1与S2之和。要计算出这两个面积，关键在于计算出交点(x0, y0)的坐标。

交点坐标，就是求解下面这个方程组的解：

$y=\frac{1}{n}x$
$y=1-\sqrt{2x-x^2}$

利用高中知识，可以得到解：

$x_0=n{y}_0=\frac{n(n+1-\sqrt{2n})}{n^2+1}$
$y_0=\frac{n+1-\sqrt{2n}}{n^2+1}$

S1是个直角三角形，很容易计算出来：
$S_1=\frac{1}{2}{x}_0{y}_0$

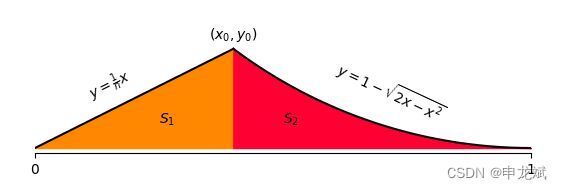
S2则需要计算一个定积分：

公式的LaTeX代码：
$S_2= \int _{x_0}^1 {(1 - \sqrt{2x-x^2})}dx$

求曲线与x轴围成的面积，有一个simpson求定积分的近似算法：

def simpsons(func, lower, upper, n):
    step = (upper - lower) / n
    x = [lower + i * step for i in range(n + 1)]
 
    res = 0
    for i in range(n+1):
        yi = func(x[i])
        if i == 0 or i == n:
            res += yi
        elif i % 2 != 0:
            res += 4 * yi
        else:
            res += 2 * yi

    res *= step / 3
    return res

第三步，编程求解

n越大，面积比越小，只需循环求解即可。

import math

# 凹三角形与L形截面的面积比
def area_percent(n):
    s0 = 1 - math.pi / 4
    y0 = (n + 1 - math.sqrt(2*n)) / (n * n + 1)
    x0 = n * y0
    s1 = 0.5 * x0 * y0
    fx = lambda x : 1 - math.sqrt(2*x-x*x)
    s2 = simpsons(fx, x0, 1.0, 100)
    percent = (s1 + s2) / s0
    return percent


def min_n(percent):
    n = 1
    while area_percent(n) >= percent:
        n += 1
    print(f'面积比小于：{percent:6.2%}，n最小为{n}')
    return n


assert round(area_percent(2), 4) == 0.3646
assert min_n(0.1) == 15
min_n(0.001)

最后的答案是：2240

积分公式

如果有更多的大学数学知识，或者用mathmatica等工具，还可以直接把S2那个积分公式计算出来：

$\frac{1-x}{2}\sqrt{2x-x^2}+x+{\sin }^{-1}(\sqrt{1-\frac{x}{2}})+C$

这样不用simpson积分，也可以计算出面积S2。

# 凹三角形与L形截面的面积比
def area_percent(n):
    s0 = 1 - math.pi / 4
    y0 = (n + 1 - math.sqrt(2*n)) / (n * n + 1)
    x0 = n * y0
    s1 = 0.5 * x0 * y0
    int_fx = lambda x: math.sqrt(2*x - x*x) * (1-x) / 2 + x + math.asin(math.sqrt(1-x/2))
    s2 = int_fx(1) - int_fx(x0)
    percent = (s1 + s2) / s0
    return percent