Python吴恩达深度学习作业2 -- 用神经网络思想实现逻辑回归

用神经网络思想实现Logistic回归

将学习如何建立逻辑回归分类器用来识别猫。 这项作业将引导你逐步了解神经网络的思维方式，同时磨练你对深度学习的直觉。

说明：
除非指令中明确要求使用，否则请勿在代码中使用循环（for / while）。

你将学习以下内容：

• 建立学习算法的一般架构，包括：
  • 初始化参数
  • 计算损失函数及其梯度
  • 使用优化算法（梯度下降）
• 按正确的顺序将以上所有三个功能集成到一个主模型上。

1- 安装包

首先，让我们运行下面的单元格，以导入作业中所需的包。

• numpy 是Python科学计算的基本包。
• h5py是一个常用的包，可以处理存储为H5文件格式的数据集。
• matplotlib是一个著名的Python图形库。
• 这里最后通过PIL和scipy 使用你自己的图片去测试模型效果。

import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage
from lr_utils import load_dataset

%matplotlib inline

2- 问题概述

问题说明：你将获得一个包含以下内容的数据集（“data.h5”）：

• 标记为cat（y = 1）或非cat（y = 0）的m_train训练图像集
• 标记为cat或non-cat的m_test测试图像集
• 图像维度为（num_px，num_px，3），其中3表示3个通道（RGB）。 因此，每个图像都是正方形（高度= num_px）和（宽度= num_px）。

你将构建一个简单的图像识别算法，该算法可以将图片正确分类为猫和非猫。
让我们熟悉一下数据集吧， 首先通过运行以下代码来加载数据。

train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()

我们在图像数据集（训练和测试）的末尾添加了“_orig”，以便对其进行预处理。预处理后，我们将得到train_set_x和test_set_x（标签train_set_y和test_set_y不需要任何预处理）。

train_set_x_orig和test_set_orig的每一行都是代表图像的数组。你可以通过运行以下代码来可视化示例。还可以随意更改index值并重新运行以查看其他图像。

index = 5
plt.imshow(train_set_x_orig[index])
print ("y = " + str(train_set_y[:, index]) + ", it's a '" + classes[np.squeeze(train_set_y[:, index])].decode("utf-8") +  "' picture.")

y = [0], it's a 'non-cat' picture.

深度学习中的许多报错都来自于矩阵/向量尺寸不匹配。 如果你可以保持矩阵/向量的尺寸不变，那么将消除大多错误。

练习： 查找以下各项的值：

• m_train（训练集示例数量）
• m_test（测试集示例数量）
• num_px（训练图像的高度训练图像的宽度）

请记住，“ train_set_x_orig”是一个维度为（m_train，num_px，num_px，3）的numpy数组。 例如，你可以通过编写“ train_set_x_orig.shape [0]”来访问“ m_train”。

m_train = train_set_x_orig.shape[0]
m_test = test_set_x_orig.shape[0]
num_px = train_set_x_orig.shape[1]

print ("Number of training examples: m_train = " + str(m_train))
print ("Number of testing examples: m_test = " + str(m_test))
print ("Height/Width of each image: num_px = " + str(num_px))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_set_x shape: " + str(train_set_x_orig.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x shape: " + str(test_set_x_orig.shape))
print ("test_set_y shape: " + str(test_set_y.shape))

Number of training examples: m_train = 209
Number of testing examples: m_test = 50
Height/Width of each image: num_px = 64
Each image is of size: (64, 64, 3)
train_set_x shape: (209, 64, 64, 3)
train_set_y shape: (1, 209)
test_set_x shape: (50, 64, 64, 3)
test_set_y shape: (1, 50)

为了方便起见，你现在应该以维度(num_px * num_px * 3, 1)的numpy数组重塑维度（num_px，num_px，3）的图像。 此后，我们的训练（和测试）数据集是一个numpy数组，其中每列代表一个展平的图像。 应该有m_train（和m_test）列。

练习： 重塑训练和测试数据集，以便将大小（num_px，num_px，3）的图像展平为单个形状的向量(num_px * num_px * 3, 1)。

当你想将维度为（a，b，c，d）的矩阵X展平为形状为(b * c * d, a)的矩阵X_flatten时的一个技巧是：

X_flatten = X.reshape（X.shape[0]，-1）.T ＃ 其中X.T是X的转置矩阵

arr.shape # (a, b)
arr.reshape(m, -1) # 改变维度为m行，d列（-1表示列数自动计算，$d=a\ast b/m$）
arr.reshape(-1, m) # 改变维度为d行，m列（-1表示行数自动计算，$d=a\ast b/m$）

-1的作用就在此：自动计算dL：d=数组或者矩阵里面所有的元素个数/c，d必须是整数，不然报错

train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T

print ("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
print ("sanity check after reshaping: " + str(train_set_x_flatten[0:5,0]))

train_set_x_flatten shape: (12288, 209)
train_set_y shape: (1, 209)
test_set_x_flatten shape: (12288, 50)
test_set_y shape: (1, 50)
sanity check after reshaping: [17 31 56 22 33]

为了表示彩色图像，必须为每个像素指定红、绿、蓝色通道（RGB），因此像素值实际上是一个从0到255的三个数字的向量。

机器学习中一个常见的预处理步骤是对数据集进行居中和标准化，这意味着你要从每个示例中减去整个numpy数组的均值，然后除以整个numpy数组的标准差。但是图片数据集则更为简单方便，并且只要将数据集的每一行除以255（像素通道的最大值），效果也差不多。

在训练模型期间，你将要乘以权重并向一些初始输入添加偏差以观察神经元的激活。然后，使用反向梯度传播以训练模型。但是，让特征具有相似的范围以至渐变不会爆炸是非常重要的。

开始标准化我们的数据集吧！

train_set_x = train_set_x_flatten / 255.
test_set_x = test_set_x_flatten / 255.

你要记住的内容：
预处理数据集的常见步骤是：

• 找出数据的尺寸和维度（m_train, m_test, num_px等）
• 重塑数据集，以使每个示例都是大小为(num_px \ num_px \ 3, 1)的向量
• "标准化"数据

3- 学习算法的一般架构

现在是时候设计一种简单的算法来区分猫图像和非猫图像了。

你将使用神经网络思维方式建立Logistic回归。下图说明了为什么“逻辑回归实际上是一个非常简单的神经网络！”

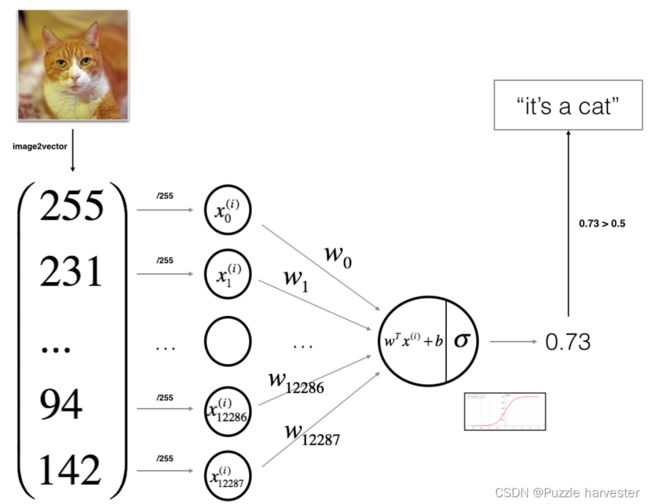
算法的数学表达式：
对于一个样列$x^{(i)}$：
$$z^{(i)}=w^T{x}^{(i)}+b$$
$${\hat{y}}^{(i)}=a^{(i)}=sigmoid(z^{(i)})$$
$$L(a^{(i)},y^{(i)})=-y^{(i)}\log (a^{(i)})-(1-y^{(i)})\log (1-a^{(i)})$$

然后通过对所有训练样本求和来计算成本:
$$J=\frac{1}{m}\sum _{i=1}^{m}L(a^{(i)},y^{(i)})$$

关键步骤：

在本练习中，你将执行以下步骤：

• 初始化模型参数
• 通过最小化损失来学习模型参数
• 使用学习到的参数进行预测（在测试集上）
• 分析结果并得出结论

4- 构建算法的各个部分

建立神经网络的主要步骤是：

1. 定义模型结构（例如输入特征的数量）
2. 初始化模型的参数
3. 循环：
   • 计算当前损失（正向传播）
   • 计算当前梯度（向后传播）
   • 更新参数（梯度下降）

你通常会分别构建1-3，然后将他们集成到一个称为“model()”的函数中。

4.1- 辅助函数

练习：使用"Python基础"中的代码，实现sigmoid()。如上图所示，你需要计算$sigmoid(w^{T}x+b)=\frac{1}{1+e^{-(w^{T}x+b)}}$去预测。

使用np.exp()。

def sigmoid(z):
    s = 1 / (1 + np.exp(-z))
    return s

print ("sigmoid([0, 2]) = " + str(sigmoid(np.array([0,2]))))

sigmoid([0, 2]) = [0.5        0.88079708]

4.2- 初始化参数

练习：在下面的单元格中实现参数初始化。你必须将w初始化为零的向量。如果你不知道要使用什么numpy函数，请在Numpy库的文档中查找np.zeros()。

def initalize_with_zeros(dim):
    w = np.zeros((dim, 1))
    b = 0
    
    assert(w.shape == (dim, 1))
    assert(isinstance(b, float) or isinstance(b, int))
    
    return w, b

dim = 2
w, b =initalize_with_zeros(dim)
print ("w = " + str(w))
print ("b = " + str(b))

w = [[0.]
 [0.]]
b = 0

对于图像输入，w的维度为(num_px $\times$ num_px $\times$ 3, 1)。

4.3- 前向和后向传播

现在，你的参数已初始化，你可以执行“向前”和“向后”传播步骤来学习参数。

练习：实现函数propagate()来计算损失函数及其梯度。

提示：

正向传播：

• 得到X
• 计算$A=\sigma (w^{T}X+b)=(a^{(0)},a^{(1)},...,a^{(m-1)},a^{(m)})$
• 计算损失函数：$J=-\frac{1}{m}{\sum }_{i=1}^m{y}^{(i)}\log (a^{(i)})+(1-y^{(i)})\log (1-a^{(i)})$

你将要使用到以下两个公式：
$$\frac{\partial J}{\partial w}=\frac{1}{m}X(A-Y{)}^T$$
$$\frac{\partial J}{\partial b}=\frac{1}{m}\sum _{i=1}^m(a^{(i)}-y^{(i)})$$

def propagate(w, b, X, Y):
    """
    实现前向传播的代价函数及其梯度
    参数：
        w：权重，大小为(num_px * num_px * 3,1)的numpy数组
        b：偏量
        X：数据大小(num_px * num_px * 3，样本数量)
        Y：“label”向量(如果非猫则为0，如果猫则为1)，大小为(1，样本数量)
    返回值：
        cost：logistic回归的代价
        dw：损失相对于w的梯度，因此形状与w相同
        db：损失相对于b的梯度，因此形状与b相同
    """
    m = X.shape[0]
    
    # 计算A、代价
    A = sigmoid(np.dot(w.T, X) + b) 
    cost = -1 / m * np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A))
    # 计算梯度
    dw = 1 / m * np.dot(X, (A - Y).T)
    db = 1 / m * np.sum(A - Y)
    
    assert(dw.shape == w.shape)
    assert(db.dtype == float)
    cost = np.squeeze(cost)
    assert(cost.shape == ())
    
    grads = {
        "dw":dw,
        "db":db
    }
    
    return grads, cost

w, b, X, Y = np.array([[1], [2]]), 2, np.array([[1, 2], [3, 4]]), np.array([[1, 0]])
grads, cost = propagate(w, b, X, Y)
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
print ("cost = " + str(cost))

dw = [[0.99993216]
 [1.99980262]]
db = 0.49993523062470574
cost = 6.000064773192205

d）优化函数

• 初始化参数。
• 计算损失函数及其梯度。
• 使用梯度下降来更新参数。

练习：写下优化函数。目标是通过最小化损失函数J来学习w和b。对于参数$\theta$，关系规则为$\theta =\theta -\alpha d\theta$其中$\alpha$是学习率。

def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
    """
    该函数通过运行梯度下降算法来优化w和b
    参数：
        w —— 权重，一个大小为(num_px * num_px * 3,1)的numpy数组
        b —— 偏差
        X —— 图像的数据(num_px * num_px * 3，样本数量)
        Y —— “label”向量(如果非猫则为0，如果猫则为1)，形状为(1，样本数量)
        num_iterations —— 优化循环的迭代次数
        learning_rate —— 梯度下降更新规则的学习速率
        print_cost —— True表示每100步打印一次损失
    返回值：
        Params —— 包含权重w和偏差b的字典
        grads —— 包含相对于代价函数的权重和偏差的梯度的字典
        costs —— 列出优化过程中计算的所有成本，这将用于绘制学习曲线。
    """
    costs = []
    for i in range(num_iterations):
        grads, cost = propagate(w, b, X, Y)
        
        dw = grads["dw"]
        db = grads["db"]
        
        w = w - learning_rate * dw
        b = b - learning_rate * db
        
        if i % 100 == 0:
            costs.append(cost)
            
        if print_cost and i % 100 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))
    
    params = {
        "w":w,
        "b":b
    }
    
    grads = {
        "dw":dw,
        "db":db
    }
    
    return params, grads, costs

params, grads, costs = optimize(w, b, X, Y, num_iterations= 100, learning_rate = 0.009, print_cost = False)

print ("w = " + str(params["w"]))
print ("b = " + str(params["b"]))
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
print(costs)

w = [[0.1124579 ]
 [0.23106775]]
b = 1.5593049248448891
dw = [[0.90158428]
 [1.76250842]]
db = 0.4304620716786828
[6.000064773192205]

练习：上一个函数将输出学习到的w和b。我们能够使用w和b来预测数据集X的标签。实现predict()函数。预测分类有两个步骤：

1. 计算$\hat{Y}=A=\sigma (w^{T}X+b)$
2. 将a的项转换为0(如果激活<=0.5)或1(如果激活>0.5)，并将预测结果存储在向量“Y_prediction”中。如果愿意，可以在for循环中使用if / else语句。

def predict(w, b, X):
    """
    使用学习到的逻辑回归参数(w, b)预测标签是0还是1
    参数：
        w —— 权重，一个大小为(num_px * num_px * 3, 1)的numpy数组
        b —— 偏差
        X —— 图像的数据(num_px * num_px * 3，样本数量)
    返回值：
        Y_prediction —— numpy数组(向量)，包含X中样本的所有预测(0/1)
    """
    m = X.shape[1]
    Y_prediction = np.zeros((1, m))
    w = w.reshape(X.shape[0], 1)
    # w: (a,1),x: (a,m)=>w.T*x=>(1,m)
    
    A = sigmoid(np.dot(w.T, X) + b)
    
    for i in range(A.shape[1]):
        
        if A[0, i] <= 0.5:
            Y_prediction[0, i] = 0
        else:
            Y_prediction[0, i] = 1
    
    assert(Y_prediction.shape == (1, m))
    
    return Y_prediction

print ("predictions = " + str(predict(w, b, X)))

predictions = [[1. 1.]]

你需要记住以下几点：

你已经实现了以下几个函数：

• 初始化(w, b)
• 迭代优化损失以及学习参数(w, b):
  • 计算损失及梯度
  • 使用梯度下降更新参数
• 使用学到的(w, b)来预测给定示例集的标签

5- 将所有功能合并到模型中

现在，将所有构件（在上一部分实现的功能）以正确的顺序放在一起，从而得到整体的模型结构。

**练习：**实现模型功能，使用以下符号：

• Y_predication对测试集的预测
• Y_predication_train对训练集的预测
• w，损失，optimize()输出的梯度

def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):
    """
    通过调用之前实现的函数来构建逻辑回归模型
    参数：
        X_train —— 由图像数组(num_px * num_px * 3, m_train)表示的训练集
        Y_train —— 由图像为(1,m_train)的numpy数组(向量)表示的训练标签
        X_test —— 由图像数组(num_px * num_px * 3, m_test)表示的测试集
        Y_test —— 由图像为(1,m_test)的numpy数组(向量)表示的测试标签
        num_iterations —— 表示优化参数的迭代次数的超参数
        learning_rate —— 表示在optimize()的更新规则中使用的学习率的超参数
        print_cost —— 设置为true，每100次迭代打印一次开销
    返回值：
        d —— 包含模型信息的字典。
    """
    
    # Step1：初始化参数为0
    w, b = initalize_with_zeros(X_train.shape[0])
    
    # Step2：梯度下降
    parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
    
    # Step3：从字典“parameters”中检索参数w和b
    w = parameters["w"]
    b = parameters["b"]
    
    # Step4：预测
    Y_prediction_test = predict(w, b, X_test)
    Y_prediction_train = predict(w, b, X_train)
    
    print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
    print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
    
    d = {
        "costs": costs,
         "Y_prediction_test": Y_prediction_test, 
         "Y_prediction_train" : Y_prediction_train, 
         "w" : w, 
         "b" : b,
         "learning_rate" : learning_rate,
         "num_iterations": num_iterations
    }
    
    return d

d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 1, print_cost = True)

Cost after iteration 0: 0.011789
Cost after iteration 100: 0.009200
Cost after iteration 200: 0.066217
Cost after iteration 300: 0.051450
Cost after iteration 400: 0.014240
Cost after iteration 500: 0.018525
Cost after iteration 600: 0.002108
Cost after iteration 700: 0.001510
Cost after iteration 800: 0.001267
Cost after iteration 900: 0.001128
Cost after iteration 1000: 0.001031
Cost after iteration 1100: 0.000955
Cost after iteration 1200: 0.000893
Cost after iteration 1300: 0.000841
Cost after iteration 1400: 0.000795
Cost after iteration 1500: 0.000755
Cost after iteration 1600: 0.000719
Cost after iteration 1700: 0.000687
Cost after iteration 1800: 0.000657
Cost after iteration 1900: 0.000631
train accuracy: 100.0 %
test accuracy: 68.0 %

评价：训练准确性接近100％。 这是一个很好的情况：你的模型正在运行，并且具有足够的容量来适合训练数据。 测试误差为68％。 考虑到我们使用的数据集很小，并且逻辑回归是线性分类器，对于这个简单的模型来说，这实际上还不错。 但请放心，下周你将建立一个更好的分类器！

此外，你会看到该模型明显适合训练数据。 在本专业的稍后部分，你将学习如何减少过度拟合，例如通过使用正则化。 使用下面的代码（并更改index变量），你可以查看测试集图片上的预测。

index = 1
plt.imshow(test_set_x[:,index].reshape((num_px, num_px, 3)))
print ("y = " + str(test_set_y[0,index]) + ", you predicted that it is a \"" + classes[int(d["Y_prediction_test"][0,index])].decode("utf-8") +  "\" picture.")

y = 1, you predicted that it is a "cat" picture.

让我们绘制损失函数和梯度吧。

squeeze()函数:

作用:移除数组中维度为1的维度。

参数:axis: 选择数组中的某一维度移除, 如果选择形状输入大于1的轴，则会引发错误。

costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()

解释：

损失下降表明正在学习参数。 但是，你看到可以在训练集上训练更多模型。 尝试增加上面单元格中的迭代次数，然后重新运行这些单元格。 你可能会看到训练集准确性提高了，但是测试集准确性却降低了。 这称为过度拟合。

6- 进一步分析

让我们对其进行进一步分析，并研究如何选择学习率$\alpha$。

学习率的选择

提醒：

为了使梯度下降起作用，你必须明智地选择学习率。 学习率$\alpha$决定我们更新参数的速度。 如果学习率太大，我们可能会“超出”最佳值。 同样，如果太小，将需要更多的迭代才能收敛到最佳值。 这也是为什么调整好学习率至关重要。

让我们将模型的学习曲线与选择的几种学习率进行比较。 运行下面的单元格。 这大约需要1分钟。 还可以尝试与我们初始化要包含的“ learning_rates”变量的三个值不同的值，然后看看会发生什么。

learning_rates = [0.01, 0.001, 0.0001]
models = {}
for i in learning_rates:
    print ("learning rate is: " + str(i))
    models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
    print ('\n' + "-------------------------------------------------------" + '\n')

for i in learning_rates:
    plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))

plt.ylabel('cost')
plt.xlabel('iterations')

legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()

learning rate is: 0.01
train accuracy: 72.2488038277512 %
test accuracy: 42.00000000000001 %

-------------------------------------------------------

learning rate is: 0.001
train accuracy: 65.55023923444976 %
test accuracy: 34.0 %

-------------------------------------------------------

learning rate is: 0.0001
train accuracy: 65.55023923444976 %
test accuracy: 34.0 %

-------------------------------------------------------

解释：

• 不同的学习率会带来不同的损失，因此会有不同的预测结果。
• 如果学习率太大（0.01），则成本可能会上下波动。 它甚至可能会发散（尽管在此示例中，使用0.01最终仍会以较高的损失值获得收益）。
• 较低的损失并不意味着模型效果很好。当训练精度比测试精度高很多时，就会发生过拟合情况。
• 在深度学习中，我们通常建议你：
  • 选择好能最小化损失函数的学习率。
  • 如果模型过度拟合，请使用其他方法来减少过度拟合。

7-使用自己的图像进行测试

你可以使用自己的图像并查看模型的预测输出。 要做到这一点：

 1. 单击此笔记本上部栏中的 "File"，然后单击"Open" 以在Coursera Hub上运行。
 2. 将图像添加到Jupyter Notebook的目录中，在"images"文件夹中
 3. 在以下代码中更改图像的名称
 4. 运行代码，检查算法是否正确（1 = cat，0 = non-cat）！

import imageio
from skimage.transform import resize

## START CODE HERE ## (PUT YOUR IMAGE NAME) 
my_image = "my_image4.jpg"   # 修改你图像的名字
## END CODE HERE ##

# We preprocess the image to fit your algorithm.
fname = "images/" + my_image                       # 图片位置     
image = np.array(imageio.imread(fname))            # 读入图片为矩阵
print(image.shape)

# print(num_px)
# 先把图片放缩到 64x64
# 转置图片为 (num_px*num_px*3, 1)向量
my_image = resize(image, output_shape=(num_px, num_px)).reshape((1, num_px * num_px * 3)).T
print(my_image)

my_predicted_image = predict(d["w"], d["b"], my_image)  # 用训练好的参数来预测图像

plt.imshow(image)

# print(classes)
print("y = " + str(np.squeeze(my_predicted_image)) + ", your algorithm predicts a \"" + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") +  "\" picture.")

(449, 328, 3)
[[0.86241582]
 [0.87787218]
 [0.74805296]
 ...
 [0.44083158]
 [0.38674671]
 [0.3469308 ]]
y = 1.0, your algorithm predicts a "cat" picture.

此作业要记住的内容：

1. 预处理数据集很重要。
2. 如何实现每个函数：initialize（），propagation（），optimize（），并用此构建一个model（）。
3. 调整学习速率（这是“超参数”的一个示例）可以对算法产生很大的影响。 你将在本课程的稍后部分看到更多示例！