【机器学习算法】聚类算法-4 模糊聚类 密度聚类，如何判断超参数：数据群数

目录

聚类算法

模糊聚类法

密度聚类法

DBSCAN的介绍

2个概念密度可达（Density-Reachable）和密度相连（Density-Connected）

DBSCAN的优缺点

数据群数的判断

R-Squared（R2）

semi-Partial R-Squared

轮廓系数

总结

---

我的主页：晴天qt01的博客_CSDN博客-数据分析师领域博主

目前进度：第四部分【机器学习算法】

聚类算法

昨天我们讲了划分聚类法，他们的的聚类结果要么是1要么是0,1代表就是这类，0代表不是这类。代表作就是K-means

模糊聚类法

EM法

昨天我们讲了划分聚类法，他们的的聚类结果要么是1要么是0,1代表就是这类，0代表不是这类。代表作就是K-means，

这些都是hard（Exclude） Clusterng

硬聚类。排他性的聚类方法

还有一种聚类方法，是软聚类，非排他性的聚类方法，soft （Non-Exclusive）Clustering

比如EM方法。（相当于K-means的软方法）

这个方法也是数据挖掘中公认的十大必学的方法，

 

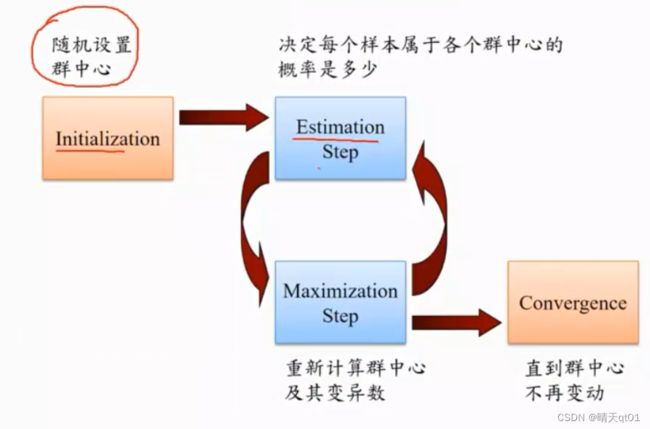
同样，我们要先设置群中型，然后计算每个样本属于各个群中心的概率是多少，然后根据这个概率来重新计算群中心的位置，然后再根据群中心来确定每个样本属于群中心的概率

上面说的动作需要一直重复做，直到群中心不再变动为止。

Kmeans的算法也是随机的设置群中心，然后根据群中心与点的距离关系，来设定概率，但是它的概率只有1和0。

也就是kmeans分为4个步骤

步骤1：随机确定群中心，

步骤2：根据群中心与点的距离关系，来确定资料点是属于分类1还是分类2.

步骤3：根据分类的资料点，出现确定群中心，然后计算方差。

步骤4：直到群中心不再变化，

一个资料点只能属于一群，排他性的聚类。

下一波就是根据资料点重新计算群中心。直到群中心位置不再改变位置。

其实Kmeans是EM的特殊形态。EM的计算更宽更泛

这样就形成每个群中心的高斯分布

步骤1：先随机设置群中心，和方差（如果要有高斯概率分布就必须设置方差。）我们就可以得到每个群的高斯分布

步骤2：计算每个资料点属于哪个群中心，这时我们计算距离，如果距离群中心越近，那么概率就越大，反之概率就越小，这个概率值就属于0或者1。

步骤3：利用群中心和群中心附近的资料点来计算方差。得到新的高斯分布。再进行步骤2

步骤4：直到群中心不再改变，

案例如下：

EM算法其实很复杂，这里用一个简单的例子让各位了解一下它的具体内容。

 

这个例子的案例只有一个输入变量x，这里的纵坐标没有意义，主要是有些资料点一样，为了区别所以画了上下，让你们知道是2个资料点、

我们先随机设置群中心，看第一个图，我们分了5个群，没个箭头都代表一个群中心，然后我们随机设置标准差和方差，就形成了5个高斯分布，每个点都有群，并且有它对应的概率。它对应的概率不是只有一个点哦，它其实很多群都有它对应的概率，不过可能大小比较小就是。

这时我们要重新计算这5个群中心，每个群中心都要用全部的数据点计算，因为每个点都有它对应的权重（概率），只是可能越靠近群中心的权重（概率）也就越大罢了。

我们再看第2个图，拿第一个群来举例把，群中心是不是向右靠拢了，群中心的点相对比较集中，而且对应的方差也比较大，因为点分布的比较宽（高斯分布比较扁平。）再看第3个群，它的群中心就向左移了方差因为只有3个点，变的比较细长。

我们再看最后一个群，它的群中心和方差再次根据全部的数据点进行调整了

这就是EM模糊聚类法

密度聚类法

该方法的名字叫做DBscan，当成它推出的时候还蛮轰动的，它不会死板的聚类，而是根据数据的形状去聚类。

DBSCAN解决的内容

举个例子：

上图是DBSCAN，分类效果，他会把第一个数据分为2个同心圆，因为数据有连接。

如果用的K-means的话，它就只能分为左右各一边。

我们再看第2个数据，一样的因为数据有连接，所以DBSCAN会把数据分为上下两类，而k-means就不能把两者完全分离。，只能一刀两断。

不过第3个数据，这种比较明显能分出来的，结果一般是一样的

如果是第4个数据，都比较平均分布的话，K-means因为你提前设定了3群，那它就会强制分为3块

 

DBSCAN能找到任何形状的聚类，但是他们的用处不太一样。

它是1996年提出的算法，以密度为本的空间计算方法，能精确找出离群值的数据，和k-means不一样，它不需要你去描述指定需要聚成几群，它会根据数据的分布，自动把数据分为几群，

DBSCAN的介绍

1.他可以处理noise噪音和离群值，

2.全部的离群值会被找到被标记出来，并且不会被标记到任何一个群里。

3经常被用于异常监测（anomaly Detection）

4.它需要设定2个参数，一个是半径，EPS（决定以资料点位中心，它的邻居有哪些，）minpts，在半径范围内最少的极限数据个数是多少，如果这个点的数据足够，那它就是核心点，如果低于minpts就不是核心点。

2个概念密度可达（Density-Reachable）和密度相连（Density-Connected）

密度可达（Density-Reachable）

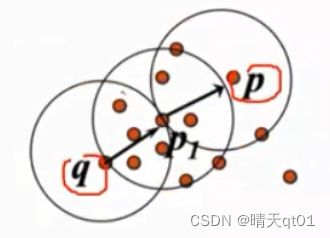
比如现在我们设定EPS为1，Minpts的值是5

现在我们q密度可达p就是现在有一点q，它周围有大于5个资料点，那么我们将它向右上角移动，移动到边缘，还是满足半径为1的范围内，数据点大于5，在移动半径单位，达到P，它周围也大于5个点，往右移动的过程中一直，注意是一直有大于5个资料点在半径范围内，那么我们就称为q密度可达p，

密度可达会运用到半径和最小资料点，

 

密度相连（Density-Connected）

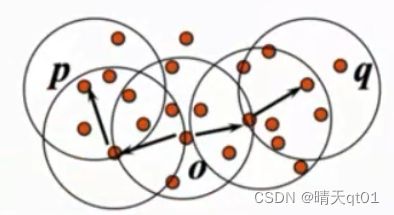
另外一个叫密度相连

P和q密度如何相连呢，如果O密度可达P。O又密度可达q，那么p和q就密度相连

 

接下来我们将利用这利用两个概念说明一下DBSCAN

 

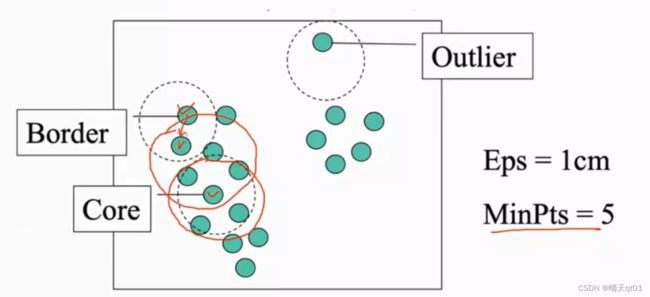
首先是border point边界点，它里面没有满足minpts，没达到5个点，但是有核心点也就是我们打钩的点，它周围有5个点。

其次是outlier point离群点，它既不满足标准，并且也不包含核心点，我们就把它叫做离群点

然后是core point核心点，半径为1的情况下，满足minpts标准。

DBSCAN案例

现在我们有9个点，x1（0,0），X2（1,0）X3（1,1）X4（2,2）X5（3,1）..

 

现在我们根据坐标把X1-X9画到坐标图上，例如x1（0，0）就代表这个点

那我们设定半径为1，minpts标准点数是3，

那么我们就可以算出每个点在半径内有几个资料点，

 

我们将每个点的类别确定下来，就是之前说了3个类别，边界点，核心点，离群点。

比如N（x1）它在半径为1的范围内标准点为3，所以就是核心点

比如N（x6）它在半径为1的范围内标准点为2，但是其中X5是核心点，所以他是边界点，

N（x9）根据定义，标准点不够，而且没有核心点，那么它就是离群点。

选择我们任意选择一个点，比如X1，它是一个核心点，我们来看看，它密度可达哪些点，

 

它密度可达x2和x7，x2密度可达x3，

那么我们就可以吧x1，x2，x3，x7聚类为一群，

然后我们再看其他的资料点，把这4个点除去的情况下，来看

接下来我们随机再挑一个，例如X4它是一个边界点，我们先跳过

看x5，它密度可达5，6,8，8又可以到4，

那么我们又可以吧5,，4,8,6可以作为一群

然后离群值X9，直接定为一群。或者删除。

DBSCAN的优缺点

优点

1.不需要事先指定群集数，

2.可以轻松处理异常（noise），不受离群值干扰。

3.它没有严格的形状，可以正确容纳多个数据点

缺点

1无法使用不同密度的数据集，如果密度不同，就会出现只集群密度密的，其他群就会被当做离群值。

如果都是密度小的话，是可以放宽参数要求的

2对超参数敏感：eps和Minpts

3如果数据过于稀疏，表现就会不佳（如果是不平均的话，放宽参数要求，可能还能分几类，平均的话就可能都识别为离群值，或者仅聚类为一群。）

4密度测量（密度可达和密度相连）会受抽样影响。（比如我们Kmeans中有100万个数据，那么我们能先拿1万来进行数据群中心的缺点，在用100万的数据进行微调，聚类就完成。如果密度聚类去抽样，可能就会发生密度不够，聚类出错的情况）

数据群数的判断

主要针对的是K-means，PAM，som，划分聚类需要先确定群数的聚类方法。

我们一般有4类方法来确定群数，

1.Sum of Square （SS）

2R-Squared（R2）

3.semi-Partial R-Squared

4.Sihoruette Coefficient（轮廓系数）

方法2和方法3，R-Squared（R2）.semi-Partial R-Squared其实和SS本质相同，就是用不同的标准测量数据我误差，这3种方法都需要人为来判断。它只是把结果show给我们。

方法4轮廓系数就比较好，自动确定群集数，自动确定，如果轮廓系数越大那么就说明该群数越合适，比如1群2群…10群中4群轮廓系数最大，那么我们就认为数据应该聚类为4群。

SS值我们已经讲过，这边说明一下R2.

R-Squared（R2）

 

直接拿一个案例来说明：

 

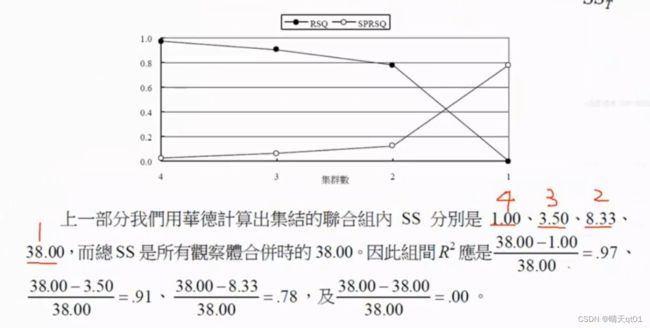
我们计算出集结联合主的SS值，分4群的值为1.0/分3群的值为3.5/分2群的值为8.33/分1群的值为38.00

R2就是用总SS值（只分一群的数值）减去该类的SS值，除以总数值。R2的实际意义就是你当群的SS值聚类我们最大的SS值还有多远。

如果R2，Rsquare的值突然下降就说明应该停止合并，采用前者的集群数

其实就是SS值的变型，看R2有没有突然的缩小。

semi-Partial R-Squared

该方法的指标其实就是将本群的SS数值减去比该群分类多一群的SS数值，然后除以总SS值（只集合一群最大）

 

也就是说，它表明的其实就是SS值增加的程度，同样的该值如果是线性增加还好，如果突然增加，这边就要把它砍掉，也就是去2群最好。

我们也可能发现3.semi-Partial R-Squared也是SS值的变型。都是看你是否突然增加，或者R2突然减少，或者SS值突然增加。

但是都要由人来决定分为几群。

轮廓系数

现在说一下轮廓系数

轮廓系数就是越大越好，越小越不好。

 

I代表每个资料点，每个资料点都有一个轮廓系数，聚类结果的好坏，就是用每个聚类结果的轮廓系数求平均来表示。

我们要算每个资料点的轮廓系数。

这里面a(i)代表的就是点a与该群内每个点距离的平均值，就是同一群资料里的平均距离这个就是a（i）

举例来说呢，

 

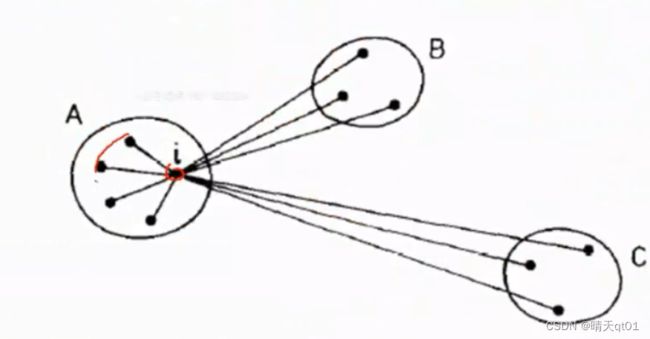
这里有我们的资料点i，群内有另外4个资料点，那么我们就计算出i与这4个资料点的欧式距离，求平均，得到的结果就a（i），它代表了群内的差异

b（i）是什么呢，其实代表的就是群外的差异，比如这里我们群外有2群，BC，一共有6个资料点b（i）就是我们先找离的近的群B，的3个资料点，求i与它们的欧式距离的平均。得到的结果就是b（i）

公式就是用群外差异减去群内差异，在除以二者的最大值进行标准化，这就符合我们聚类的精神和定义，群外差异大，群内差异小，这是轮廓系数就大，那么聚类效果就好。通常群外差异是比较大的。所以一般都是除以b（i），公式就会变成，轮廓系数的值就是=1-a(i)/b(i),

 

大部分是第一个情况，很少群内差异和群外差异一样大的，或者群内差异大于群外差异的，只有乱搞分解结果，才有可能出现下面两种情况。

这个公式考虑到各种情况，所以考虑到这种情况。

轮廓系数案例

 

这里我们将数据分为2群，左下角的资料占了3/4，每个资料都有轮廓系数，每个群的轮廓系数由大到小排序，分为1群和0群。这里的红色虚线就是所有轮廓系数的平均值，这里的平均轮廓系数大约0.7多。

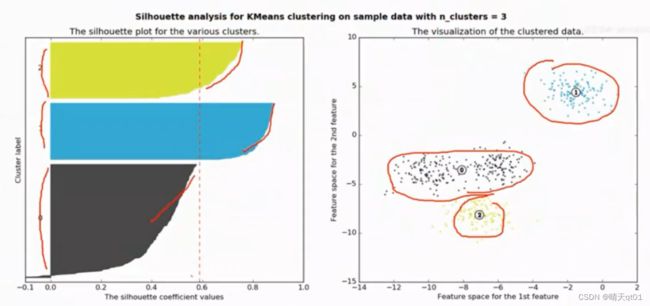
下面我们再分成3群，结果如下

 

这里的平均轮廓系数就是0.6左右。轮廓系数比较低，所以相比下，轮廓系数为2群比较合适。

至于它为什么分为绿蓝黑三轮廓系数会降低呢？会导致黄色群和黑色群的群外差异非常小群内差异可能有缩小但是群外差异变不大的情况这个值算出来就会不到0.5.

下面我们再分为4群，结果如下：

 

我们会发现，轮廓系数会提高到0.6多，提高了一点，但是还是不到0.7.

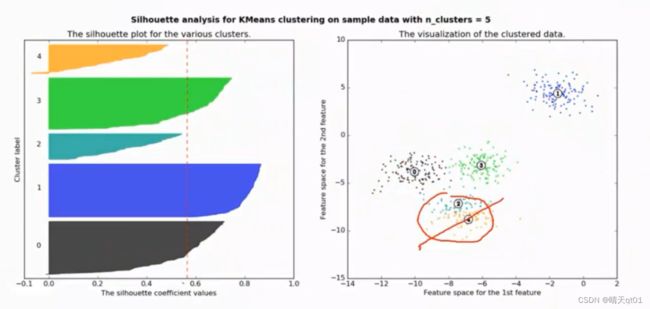
我们再把群数分为5群。

 

这里群外差异会更小，平均轮廓系数0.6不到

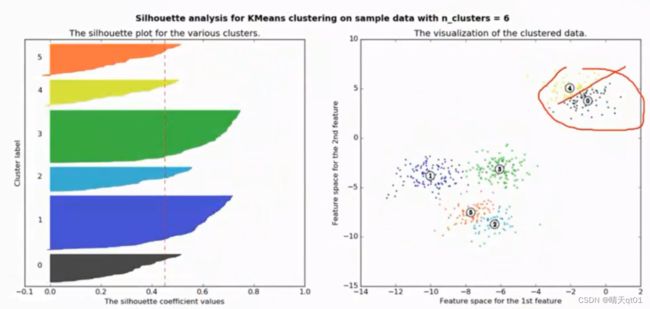
6群的情况

 

我们会发现群外差异会越来越小。就会导致轮廓系数降的比较低。0.4多

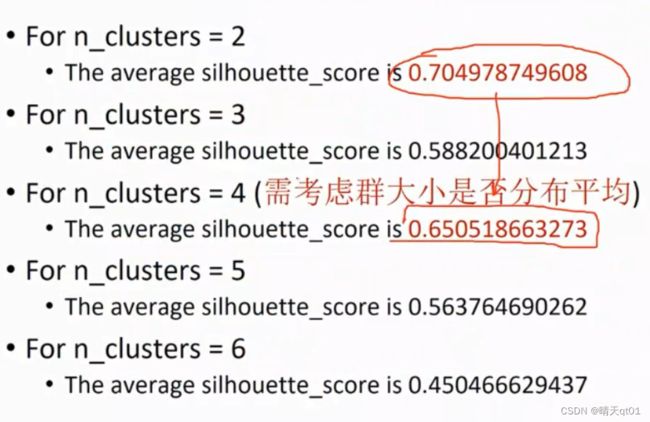
我们发现23456群的分群情况如下

 

我们发现分为2群的轮廓系数最大，2群的群外差异小，群内差异不大

4群的轮廓系数也比较大，而且每个群的资料点数量分布比较平均，所以分为4群也是完全可以接受的。

因为我们聚类都是希望每个群分布的比较平均，又希望群内群外差异比较小，我们完全可以引入一个新指标，表示聚类结果的群集数的比例。轮廓系数之考虑群内群外差异不考虑每一群的资料点数量分布。

总结

我们今天说了一个EM模糊聚类法，

还有一个是密度聚类DBSCAN的方法，

模糊聚类是一个softclustering，每个资料点隶属于各群，不过概率值不一样

密度聚类方法是以形状为根本来聚类，

还有就是群数的判断，人为查看的话就建议使用SS法和R2，SEMI-PartialR2，方法，后两个方法是SS法的衍生

当然也可以用轮廓系数，它可以自动得到合适的聚类群数。

那么我们的聚类分析就全部讲完了，下次讲关联规则。