论文精读——基于机器学习的越南生活固体废弃物预测

原文链接：https://www.sciencedirect.com/science/article/pii/S0921344920306996
备注： $R_2$即为统计学中的可决系数，用来描述拟合程度。

Abstract

原文：
The main aim of this work was to compare six machine learning (ML) - based models to predict the municipal solid waste (MSW) generation from selected residential areas of Vietnam. The input data include eight variables that cover the economy, demography, consumption and waste generation characteristics of the study area. The model simulation results showed that the urban population, average monthly consumption expenditure, and total retail sales were the most influential variables for MSW generation. Among the ML models, the random forest (RF), and k-nearest neighbor (KNN) algorithms show good predictive ability of the training data (80% of the data), with an R2 value > 0.96 and a mean absolute error (MAE) of 121.5–125.0 for the testing data (20% of the data). The developed ML models provided reliable forecasting of the data on MSW generation that will help in the planning, design and implementation of an integrated solid waste management action plan for Vietnam. The limitations of this work may be the heterogeneity of the dataset, such as the lack of data from lower administrative units in the country. In such cases, the predictive ML algorithm can be updated and re-trained in the future when the reliable data is added.

【译】
本研究旨在通过比较六种基于机器学习的模型来预测越南生活固体废弃物。

输入数据包括八个变量，涵盖研究区域的经济、人口、消费和废弃物产生特征。

模型仿真结果表明，城市人口、平均月消费支出和总零售额是影响城市生活废弃物产生的主要变量。在六类机器学习模型中，随机森林和K最近邻算法对训练数据集（80%的数据）具有良好的预测能力（决定系数>0.96），且在测试集（20%的数据）上的平均绝对误差为121.5–125.0。

基于机器学习模型的预测结果有助于越南的综合固体废弃物管理行动计划的规划、设计和实施。本研究的局限性体现在数据集的异质性，如越南下级行政部门缺乏有效数据。基于此，当未来能够获取更多的可靠数据时，可以更新和重新训练机器学习预测模型。

---

1. Introduction(partly)

文献综述节选：

为了预测城市固体废弃物的产生，已采用了不同规模的各种模型，例如直辖市，省和地区。

最初，由于基础数学的简单性和易于解释获得的结果，线性回归，组比较，投入产出分析，质量平衡以及相关分析和时间序列分析被广泛使用。 在这一先进的研究领域中，最近，机器学习（ML）方法已被证明可有效预测城市固体废弃物的产生。

Johnson et al. (2017)使用梯度提升模型来预测纽约市每周的城市生活垃圾产生量($R_2$为0.82)。Abbasi and El Hanandeh (2016)应用支持向量机（SVM）来预测澳大利亚昆士兰州的每月MSW生成量（$R_2$为0.71）。另外，还有学者部署了其他ML模型来预测不同领域的MSW生成，例如:

• SVM(Kumar et al., 2018)
• random forest (RF)(Dissanayaka and Vasanthapriyan, 2019; Kumar et al., 2018)
• 人工神经网络(ANN)(Azadi and Karimi-Jashni, 2016; Kannangara et al., 2017).

然而，这些以前的大部分集中于预测城市固体废弃物产生的工作都没有进行特征选择研究（如变量重要性评估）来确定最具影响力的输入变量，这表明无法确定输入变量对产出的作用和影响这一事实。

例如，在Johnson et al. (2017)的研究中，作者仅基于研究时间和区域的线性关系或显着性来实现特征选择，这些关系不能反映从模型中获得的结果。

因此，从实际应用的角度来看，如果对输入变量进行适当的排序和选择，将减少模型的不相关或高度相关的属性和冗余特征，从而改善模型的功能并减少收集不必要数据的需求 。(Cai et al., 2018; Kang and Ryu, 2019).

在目前的文献中，较少的预测ML算法经过训练和测试后将结果与以前的研究进行比较，例如(Adamovic et al., 2017; Johnson et al., 2017; Kannangara et al., 2017).在这些研究中，不同的机器学习技术的真正多功能性和优势或局限性仍然未知。

将各种算法用于训练和预测/或只预测将为模型的功能和局限性提供更多的技术性见解，最终将帮助用户为他们的特定任务选择合适的ML技术。

本文主要目的是为预测越南的城市生活垃圾产生量开发最佳的ML模型。具体目标可以说明如下：

1. 执行特征评估并选择输入变量（通过递归特征约简）。
2. 比较不同的ML算法以预测MSW产生。

为了实现这一目标，在这项研究中，使用了从线性，非线性和集成方法衍生的五种ML算法以及具有特征选择，重采样，重处理和调整特征的连续步骤的ANN模型。

监督测试和交叉验证（CV）程序也适用于确定特定MSW数据的最佳模型。

2. ML - based models and applications for waste prediction(partly)

本文分别使用了分类，回归，集成模型和深度学习这四种类型的监督学习算法。

1. 分类算法适用于分类结果变量，并适用于实值结果变量的回归。
2. 集成模型是一个模型中几种算法的组合。
3. 某些算法（例如KNN和SVM）同时使用分类和实值结果变量。

选择算法的主要原因如下：通过监督训练的学习能力，算法处理非线性数据的能力，检测数据集故障的能力，异构输出参数以及处理数字目标变量的能力。

2.1 Linear model(线性模型)

线性模型（即LR，逻辑回归，线性判别分析和线性判别分析）是一种统计方法，同时也是ML算法。

LR是一个线性方程，由一组特定的输入值（x）和该组输入值的预测输出（y）组成。LR和ML很容易解释和理解，但是它们也有一些局限性（即独立分布和正态分布），从而导致输出中的高偏差。

作为线性关系的特征，此方法不适用于建模高度非线性的数据。普通最小二乘线性回归（LM）的目的是发现所观察到的响应与预测的响应之间的平方和误差最低的平面。

对于实际应用，由于简单的基础算法和易于解释的结果，LM是一个有吸引力的模型。 但是，预测变量之间的共线性会导致LM模型误差较大。

2.2 Support vector machine(支持向量机)

SVM学习结合了基于实例的最近邻居学习，使用最近邻居的惰性学习分类和LR模型（Lantz，2019）。

SVM将每个数据项绘制为n维空间中的一个点（n为要素数量），并找到最能将这两个类区分开的超平面（Kuhn和Johnson，2013）。

它可以检测有助于对数据集的新点进行分类的最佳超平面。该算法可用于分类和数字预测目的。内核技巧和功能实际上是使用SVM的工具。

它使用内核技巧来修复非线性输入空间。 以线性可分离的方式，SVM将在正确分类所需类别的约束下确定最佳分割线。 通过这种方式，SVM可以挖掘单独的超平面，并选择具有最大余量的超平面。对于线性不可分的情况，SVM使用不可分离的线确定软边距，然后获得一条称为非线性决策边界的线（即内核技巧）。

SVM擅长解决分类问题，并且更常用于预测离散输出（Theobald，2018）。 它已被用于解决诸如城市固体废弃物预测，废物分类和能源回收等回归问题（Abdallah等，2020）。 此外，支持向量机不太可能导致过度拟合，并且减少了误差和模型尺寸（Li等，2010）。

2.3 Cubist模型树

Cubist模型树是Quinlan（1992）描述的面向预测的回归模型，并基于训练集中最近的邻居进行了其他修正（Quinlan，1993）。该模型使用线性组合进行组合的，如等式1-2所示(Kuhn and Johnson, 2013)：
$${\hat{y}}_{par}=ax{\hat{y}}_k+(1-a)x{\hat{y}}_p\text{\hspace{1em}(1-2)}$$
其中，${\hat{y}}_k$是当前算法的预测输出值；${\hat{y}}_p$来自树中它上面的父模型； a是平滑系数。

Cubist算法是一种模型树，它使用特定的线性模型创建一组规则（〜委员会）。

对于每个规则，Cubist算法使用“ if and then”语句并创建一个线性方程式，该线性方程式用于计算结果。其他启发式方法，例如修剪和增强，可改善预测结果的质量(Radziwill, 2019)。

此外，Cubist算法有两个参数，它们可以是默认值或可调参数。这两个参数是委员会，即可用于增强操作和邻居的数量，以及用于纠正基于规则的预测的实例数量。 到目前为止，还没有使用Cubist算法来预测固体废物的产生率。

2.4 Random forest

RF被认为是功能最强大的ML算法之一。

它是由Brieman (2010)开发的，结合了随机子空间和装袋 (Nisbet et al., 2009)。

它涉及树预测器的组合，其中每棵树都依赖于对森林中所有树使用相同分布的，独立采样的随机向量的值(Breiman，2001)。RF产生的最终输出基于所有树木预测的平均值(Zhou et al., 2019)。

训练RF的基本过程可以描述如下(Breiman,2001; Kuhn and Johnson, 2013; Zhou et al., 2019)：

1. 从数据集的原始样本中，获取一个引导样本，该样本是随机选择的替换样本。
2. 仅考虑数据的一部分子集，使用bootstrapp方法创建树。在每棵树的节点上，从mtry的随机选择子集（在每个节点上测试的不同预测变量的数量）中选择最佳拆分。
3. 重复步骤2，将建立新的bootstrap数据，直到建立最佳数目的树（ntree）。

2.5 k-nearest neighbor(KNN)

KNN基于聚类算法，这是一种有监督的学习技术，用于根据新数据点到附近数据点的位置对它们进行分类(Walker, 2018)。

KNN使用训练集中的K个最近邻居样本预测新的样本数据(Guo et al.,2003)。KNN没有专用模型，而是存储整个数据集，因此，该算法无需学习。 它使用诸如k-d树之类的复杂数据结构，在预测过程中观察并连接新模式。

对于测试数据中的每个实例，该函数将使用欧几里得距离（平面中两点之间的距离）标识KNN，其中k是用户指定的数字(Lantz,2019)。此外，KNN的错误率低，且数据量大，并且可以使用较少的特征（较小的维数）以最佳方式找到点的最近邻居(Forsyth, 2019)。

KNN是可用于回归和解决分类问题的算法。 对于回归问题，通过KNN进行的预测基于k个最相似实例的均值或中位数。KNN被认为更适合于低维数据，而不是输入数量更多的数据。

迄今为止，只有一项研究使用KNN预测废物的产生（Abdallah等人，2020年）。 Abbasi和El Hanandeh（2016）报告的$R_2$值低至0.51，其中每月废弃物产生量是通过使用废弃物产生时间序列数据集进行训练来预测的。

2.6 Artificial neural network

ANN是一种计算系统，包括多层排列的神经元（输入-隐藏-输出）。

人工神经网络由于具有强大的容错能力，并且适合描述多元系统中变量之间的复杂关系，因此已在许多废物管理研究中得到应用(Abdallah et al., 2020)。另一方面，深度神经网络（DNN）是一种输入输出映射系统，具有许多隐藏层，可处理不同级别的数据抽象。

DNN的核心思想不仅是学习输入和输出之间的非线性映射，而且是学习数据的底层结构(Karhunen et al., 2015)。DNN模型使用反向误差传播算法从训练数据中学习模式，其中，来自输出的误差或反馈信号将向后传播，以调整神经网络权重并使最终输出的误差最小(Chollet and Allaire, 2018)。DNN的结构包括输入，隐藏和输出层。

使用者可以使用试错法来优化隐藏层中神经元的数量，激活功能，学习率，动量项和历元。 在本研究中，DNN模型由四层构成，即输入层，具有64个神经元的第一隐藏层，具有32个神经元的第二隐藏层，一个输出层和“ relu”激活功能。

单隐藏层前馈神经网络体系结构已经常用于预测废物产生率。(Adamovic et al., 2017; Azadi and Karimi-Jashni, 2016; Kannangara et al.,2018; Kontokosta et al., 2018; Kumar et al., 2018)。

3. Materials and methods

3.1 Solid waste data collection

数据来源于越南国家统计局((https://www.gso.gov.vn/Default_en.aspx?tabid=766)。获得了两个数据集，即详细数据集和删节数据集。详细的数据集由十个变量组成：

• 省份详细信息
• 城市人口(Upo)： 每个省的城镇人口。Thousandsof people
• 消费品零售总额(Trs): 消费者零售总额。USD/month
• 人均月收入(Amipp)： 按当前价格计算的全省人均月平均收入。USD/province/month
• 人均房屋面积(Ashpp): 每人在家中所占的平均面积(面积)。$m^2$/person
• 人口密度(Pd)： 单位面积人数。Person/$k{m}^2$
• 人均平均每月消费支出(Amcepp)： 人均每月平均消费支出，以消费品零售总额除以人口计算。USD/person/month
• 总医院病床(Thb): 病床总数。Beds
• 每个省的总居住土地(Trl)： 住宅用地总面积。Thousands ha
• 每天收集的固体废物总量(Tswpd)(输出变量)：全省每天收集的固体废物总量，收集率通常占城市固体废弃物总产生量的95-100％。单位：Ton/province/day

删节的数据集包括每天收集的固体废物总量(Tswpd)和城市人口数据(Upo)。

The detailed dataset has 63 sets (i.e. rows) corresponding to the provincial administrative units of Vietnam from the year 2016 and the abridged dataset has 189 sets from the years 2015 to 2017, respectively.

从2016年开始，详细数据集具有对应于越南省级行政单位的63行，而从2015年到2017年的简化数据集则具有189行。变量具有不同的度量单位。因此，使用ML技术对它们进行了重新处理和标准化。

3.2. Input variables

表1列出了本研究中使用的描述性数据。

从越南统计数据中选择了九个变量，这些变量涵盖了经济，人口，消费和城市固体废弃物的产生方面。 这些是被认为会影响城市固体废弃物产生的潜在变量。

Tswpd是输出变量(即因变量或预测变量或目标输出)，而其他变量是输入(即自变量)。根据区域的特征，数据的可用性以及与城市固体废弃物产生有关的意识水平来选择输入变量。表1所示的标准差表示所选变量之间的显着变化。

数据分布以直方图的形式绘制，如图1所示。虚线是变量的数值众数，即数据集中最常出现的数字。 显然，除了Ashpp之外，所有功能的分布都是偏斜的。 这意味着数据不是正态分布，表明这些变量可能不适合典型的统计检验。 偏斜的分布还表明需要对数据进行预处理以提高结果的准确性，或者需要更高级的方法。

图1

表1：输入、输出变量描述

3.3 Machine learning techniques

3.3.1 Feature importance assessment(特征重要性评估)

在现代ML方法（例如RF算法）中，可以轻松处理可能导致过拟合问题的高度相关的自变量。

因此，作为一种预筛选策略，检测高或低相关变量的相关分析并不重要。在这项研究中，确定了不同输入变量的相对重要性。 特征分级使用了两种主要技术，分别是广义线性模型和多重线性模型。 另外，为了检查数据中是否存在异方差性，使用了Breusch-Pagan检验。 由于估计系数的方差趋于增加，因此数据中存在异方差会导致预测模型出现较大误差(Guerard,2013)。拒绝原假设的变量(比如统计值>临界值)，比其他的变量更重要。

因此，选择了最重要的变量作为价值预测指标，以进行进一步建模。 相对重要性通过基准评分（范围从1.0到4.0）进行了评估。 分数反映了每个变量在预测输出变量中的贡献。 在这项研究中，使用无监督学习算法和递归特征消除（RFE）技术来选择最佳变量。 RFE是使用重复CV(折叠验证)的一种简单的向后选择方法，该方法适合整个模型，并删除最弱的变量，直到确定最低数量的基本变量为止。

3.3.2 Data pre-processing and re-sampling（数据预处理和重新采样）

由于所收集数据的巨大差异，因此进行了数据转换以减少数据偏斜或异常值的影响。在这项研究中使用了诸如Center（将值除以标准偏差），Scale（从值中减去平均值）和Range（将值归一化）之类的技术。

为了最大程度地减少采样偏差并防止ML过度拟合，实施了重采样技术，以创建应用于模型的样本的随机子集，而其余数据用于确定模型的泛化能力。

因此，对于这五个ML算法，数据分为训练数据（占总数据的80％）和测试数据（占总数的20％）。此后，将K折验证法，重复验证法和留一法（LOOCV）用于训练数据。

在K折验证中，将样本集随机分成大约相等大小的K个集合，然后将K折用作验证集，而将K-1折用作测试集。

LOOCV是K折CV的一种形式，而重复CV是一种重复多次（即至少重复3次）的CV。在默认训练期间，首先使用重复CV，而其他类型的验证方法用于检查与默认重采样相比，算法是否提高了其预测性能。对于DNN算法，数据分为：80％训练和20％验证。

3.3.3 Tuning

本研究中，在评估和比较不同的ML模型期间，使用了每种算法的内部参数的默认设置。

为了进一步测试和优化这些参数，对算法进行了调整。 优化这些参数的一般方法是确定一个值范围（最小到最大值），该范围提供模型预测/预测的可靠估计，然后确定最佳参数(Johnson et al., 2017)。

在本研究中，就对隐藏层中的神经元数量，DNN模型的历元数和RF模型的ntree（要生长的树数）进行了调整。

3.3.4 Metrics of the model and software tools

使用MAE，RMSE和R2等指标评估了算法的性能，具体如下：
$$MAE=\frac{{\sum }_{i=1}^n|y_i-x_i|}{n}\text{\hspace{1em}(1-2)}$$
$$RMSE=\sqrt{\sum _{i=1}^n\frac{(y_i-x_i{)}^2}{n}}\text{\hspace{1em}(1-3)}$$
$$R^2=1-\frac{{\sum }_{i=1}^m{(y_i-x_i)}^2}{{\sum }_{i=1}^m(y_i-\overline{x_i}{)}^2}\text{\hspace{1em}(1-4)}$$
其中，n是样本数； $x_i$是模型的预测响应(即模型的预测输出值)； $y_i$是响应的实际值； $x_i$是平均估计值。

本研究中，使用了带有附加支持包的R语言成语（版本3.6.1）来计算和运行ML算法。 使用了两个主要软件包，即分类和回归训练工具（“ Caret”）和R studio中的深度学习工具（“ Keras”）。

4. Results and discussion

4.1. Feature importance of input variables and selection

先前有关废物产生和管理的研究选择了不同的变量，例如人口和社会经济地位，就业市场，该地区的企业等因素。综述略。

Studentized Breusch-Pagan检验的结果表明，数据中存在异方差（$p=7.471\times 10^6$）。 这可能会在预测模型中引起较大的误差，因为估计系数的方差将增加几倍。(Guerard, 2013).

因此，我们使用鲁棒回归测试来检测/识别导致异方差性的变量或拒绝零假设的变量(即预测变量与结果变量没有线性关系)。Upo，Amcepp和Trs的测试统计数据的绝对值分别为5.49，-3.36和3.30，大于临界值2.0。 因此，原假设可以被拒绝，Upo，Amcepp和Trs被列为最重要的变量。

相对特征重要性和相对于输入变量数量的误差值在图2中进行了量化和绘制。图中的得分反映了每个变量在预测变量Tswpd中的作用。 如图2a所示，变量Upo具有最高的重要性，而Pd的排名最低。 与Upo一起，Amcepp被确定对模型非常重要，占所有变量总重要性的45％。 另一方面，Pd和Ashpp对预测模型的贡献最小（占总数的6.3％）。

图2b所示的结果还表明，自变量的数量可能与重要性水平不成比例。 例如，变量Upo的误差值最低（RMSE：361.4； MAE：198.9； R2：0.83），表明该模型仅使用一个预测变量进行了优化。 另一方面，当模型中使用的变量数量为四个时，误差也很大（例如，RMSE为479.9）。

4.2. Comparison of algorithms

五种ML算法的结果比较如图3所示。

可以看出，RF模型的平均MAE最低，为111.10，其次是KNN（113.87），Cubist（112.04），SVM（131.07）和LM（139.37）。 利用平均MAE值和算法的稳定方面，选择了两个最佳模型，即RF和KNN。 此外，发现RF的$R^2$（RMSE）和KNN分别为0.883（RMSE 171.44）和0.832（RMSE 188.39）。

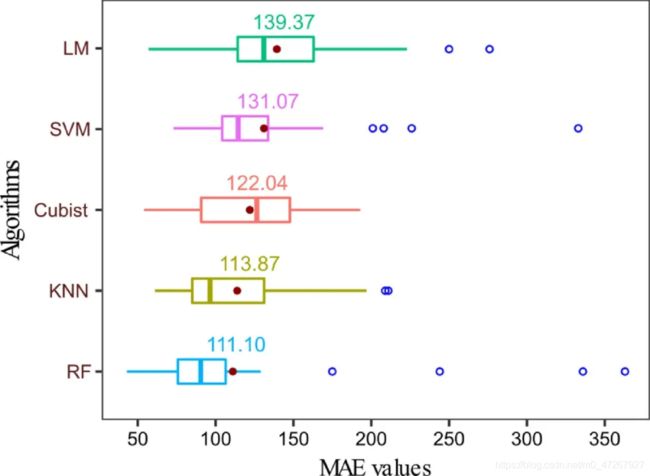
然而，先前使用ML预测城市固体废弃物产生的研究报告了关于模型预测能力的不同结果。 例如，支持向量机被认为是最佳模型，$R^2$为0.93，其次是KNN，其$R^2$为0.88，以及ANN的$R^2$为0.83(Abbasi and El Hanandeh, 2016)。

进行了重采样，变换和调整，以提高两种选定算法（RF和KNN）的性能。但是，当通过Box-Cox，Center，Scale和Log函数转换输入变量时，与不进行数据转换相比，模型的误差没有变化。

不同重采样方法的结果表明，对于RF，10倍CV达到最佳性能，最低MAE为104.34（RMSE 176.45)。而对KNN而言，发现重复CV最佳，MAE为113.87 (R2: 0.83; RMSE:188.38)。对于KNN，k值为1.0是最佳超参数，树的数量和RF的每个分割（mtry）尝试的变量数量分别为500和1.0。

在DNN的情况下，训练了2,241个参数和122个样本，历元为50个，批大小为32个。图4以MAE值和历元说明了训练和验证期间DNN的容量。

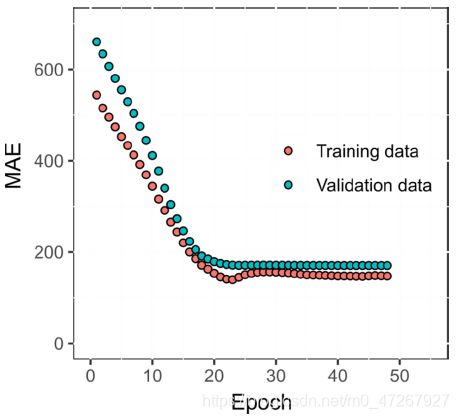
4.3 Generalization ability and application of the models

在此步骤中，使用外部数据集测试了三个开发的模型，即RF，KNN和DNN，结果分别显示在表2和图5中。发现KNN，RF和DNN的MAE和RMSE值分别为121.5和202.3、125.0和201.6、177.6和294.6。就R2值而言，最高的预测性能是针对RF和KNN的，分别为0.97和0.96（表2和图5a-b）。训练数据上三个ML模型的高度概括表明，拟合不足问题被忽略了。 就残留分数而言，RF和KNN的预测模式相似，而在DNN的MSW生成值较高时，它显示出较大的残留分数（图5c）。

预测城市固体废弃物产生的不同模型性能的比较结果(表2)：

本研究中，RF和KNN模型在训练和测试期间均显示出较高的R2值。这意味着开发的ML模型不会过度拟合或过度训练，即当模型对训练数据拟合得太好而对测试数据拟合得太低时经常遇到的问题。 在模型开发中采用的10倍CV重采样技术可防止过拟合。

相反，文献报道了测试阶段的R2值<0.80，尽管在训练阶段报告了非常高的R2值（> 0.95）以预测MSW的产生。

例如，Kumar and Samadder (2017) 开发了多个线性回归分析模型来预测城市固体废弃物的产生，在测试阶段，可生物降解部分的R2值分别为0.76和不可生物降解部分的R2值为0.64（表2）。

在另一项研究中，Kumar et al. (2018) 使用不同的ML算法开发了预测模型，在测试阶段，ANN，SVM和RF模型的R2值分别为0.75、0.74和0.66。

根据Kannangara等人（2018）的研究，用于预测城市固体废弃物产生的ANN和决策树模型在测试阶段的R2值分别为0.72和0.54。 但是，在该研究中，作者将数据集分为以下训练和测试比率：60：40、70：30、80：20、85：15和90:10，并且对于每个比率，总共随机产生了100个分区。

在这项研究中，考虑到Tswpd的值范围（即52.0–7,650吨/天；平均值：526.5±1,183.2吨/天），MAE的范围为121.5–125.0清楚地表明RF和KNN是用于预测城市固体废弃物的产生出色的模型。

此外，较高的R2值（> 0.96）证实了ML算法以最小的误差解释了输出变量的方差的事实。 所开发的ML模型可用于预测越南不同省或行政区域中的未来MSW产生量。 此外，这些预测模型对于新计划的居民区或缺乏固体废物收集数据的居民区可能是有利的。

此外，从ML模型预测的MSW产生量不仅考虑了产生的废物总量，而且还考虑了可回收废物，废物衍生材料，可生物降解废物和其他废物的产生率。 另一方面，在估算城市固体废弃物的产生量和小规模可回收废物量后，例如： 在城镇，街道上，这些可预测的ML模型可用于制定更有效的路线计划（Kontokosta等人，2018）。 尽管任何数据驱动模型的结果通常都是针对特定地区或特定过程的，但该研究有助于提供支持越南集成SWM计划的数据。

因此，该研究的结果可用于以下方面：

1. 规划和提出SW处理方案。
2. 设计垃圾填埋场建设工程。
3. 设计资源回收技术。
4. 有助于确定对MSW的产生最具影响力的变量。
5. 帮助环境经理，政策制定者和各种利益相关者制定有关越南MSW回收和资源回收的新政策。

通过仔细地筛选和选择仅一个输入要素(即城市人口(Upo))，该模型也显示出很高的预测能力。 它还显示了受城市人口激增控制/影响的不同城市生活垃圾产生方式。
未来几十年中城市人口的增长趋势（例如，据报道2009年至2019年间年均增长2.62％（CPHCSC，2019年））是城市生活垃圾产生量扩大的动机和主要原因; 尽管其他因素（例如平均每月消费支出和零售总额）在影响城市固体废弃物产生中也起着重要作用。

与收集所需的西南偏南发生率数据相比，在任何地区都可以轻松获得有关年度人口统计数据，并且对人口的预测也更容易且成本更低。这一观察结果也与Kannangara等人的发现一致(2017)，作者证明了通过普查数据使用社会经济参数，为规划和优化加拿大的废物管理业务提供了独特的机会。 本研究中使用的数据驱动的预测模型可以应用于环境工程和废物管理的其他领域和专业，并且可以应用于具有相似社会经济和人口状况的其他国家。

5 Conclusions

本文收集了来自越南的与固体废物相关的数据，并将涵盖研究区域的经济，人口统计学，固体废物消耗和废物产生特征的八个变量用作ML模型的输入，其中，城市人口，平均每月消费支出和零售总额这三项投入被认为是预测越南城市生活垃圾产生的最重要变量。

比较了包括LM，SVM，Cubist，RF，KNN和DNN在内的6种ML算法，以选择最佳的预测模型。

RF和KNN模型显示出良好的预测能力，R2值> 0.96。此外，通过一个输入变量即Upo，使用ML算法即可实现较高的预测能力。

本研究中使用的ML方法和取得的成果将帮助越南政府增加其回收实践，开发综合资源管理平台并在越南实现循环生物经济。

这项工作的局限性可能是数据集及其数量的异质性，例如缺少下级管理部门的数据。未来的研究应该进行调查，以收集来自较低居住区域（即地区，城市）的更多城市生活垃圾数据，以补充或验证该算法。因此，可以更新和重新训练用于预测MSW生成的ML算法，以获得更可靠，更准确的结果。

References

略。可见文首，下载文献进行阅读。