cs224w 图神经网络 学习笔记（五）Community Structure in Networks
课程链接：CS224W: Machine Learning with Graphs
课程视频：【课程】斯坦福 CS224W: 图机器学习 (2019 秋 | 英字)
目录
-
- 1. 前言
- 2. Network communities
- 3. Louvain algorithm——Louvain社区发现算法
- 4. BigCLAM——重叠社区发现算法 Detecting Overlapping Communities
1. 前言
在上一节的内容，我们了解了网络中的Role（角色），我们也讲到了Role和Community的区别（前者是功能相同的节点的集合，后者则是有联系的节点的集合），这一节的内容会来探讨一下Networks中的Community。
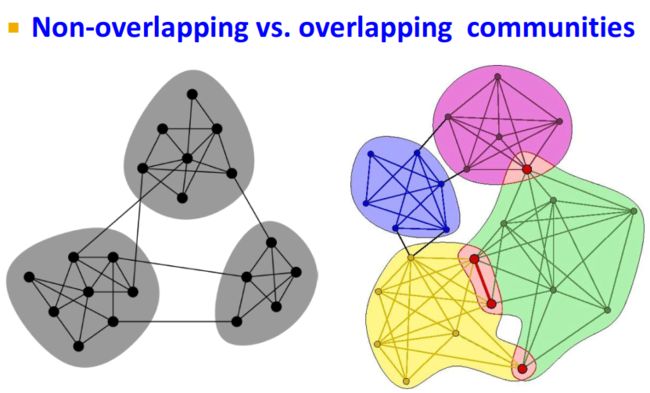
在我们的印象中，网络通常是这个样子的，就像社交网络一样：由许多个节点团（社区）联系而成，节点团内的节点联系紧密，节点团之间的节点联系稀疏。
这一节的内容就是来探讨这样一个概念图形成的原因，以及怎样去自动发掘网络中的Community。
我们可以先从社会学的角度去看待这样的概念图。
首先介绍一个很重要的概念——信息流（information flow）。这里我们需要考虑一个问题：*信息在网络中是如何流通的。*这里面又涉及到两个小问题：
为了阐述信息在网络中的流通，Mark Granovetter 教授在他的博士论文中有做过这样一项研究，他研究人们怎么获取新的工作信息，是怎样找到自己的工作的。他发现，人们通常更倾向于通过熟人（acquaintances）获取这些信息，而不是通过联系更加亲密的朋友（close friends）。这是一个比较“反常”的结论，因为在我们的印象中，我们总是觉得自己在遇到困难或事情的时候，会找更亲密的人来帮忙。
注：在英文中，acquaintance的意思是a person that you know but who is not a close friend，不会经常联系，关系上看应该要比close friends要疏远一点。close friend指每天都联系的意思。
对此，Mark Granovetter 教授给出了他的解释。
首先，他提供了两个看待友谊的观点：
对于社会中不同角色之间的友谊/联系，Mark Granovetter 教授也提供了两个角度——
First Point: Structure
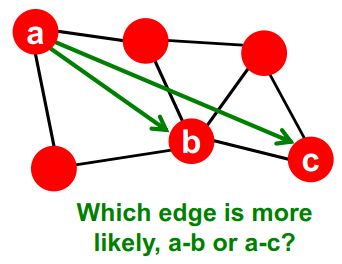
从结构的角度上看，如果网络中的两个人有一个共同的朋友，那么他们成为朋友的可能性就会增加。比如在下图中，a和b更可能成为朋友，也就是说a和b之间的边更可能产生。
Second Points: Information
从信息获取的角度上看，长范围的关系可以帮助我们获取不同的、新的信息；而经常联系的人会形成一个圈子，大家获取信息的来源是大致是一样的，从信息获取的角度来说是冗余的——这就解释了为什么我们会选择从熟人而不是密友那里获取信息。
这样的现象被称作**“Triadic closure”（三角闭合）**
Mark Granovetter 教授在上世纪六十年代就提出了这些理论，而这些理论后面才被陆续证实。
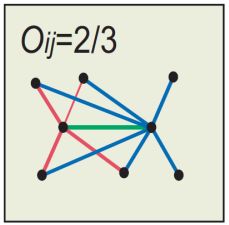
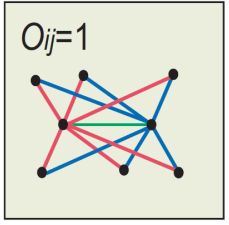
随着这个理论的发展和完善，引入了一个新的概念——Edge overlap
O i j O_{ij} Oij的分子是与节点 i i i和节点 j j j共同相连的节点集合的模，分母是除了节点 i i i和节点 j j j以外的所有节点的集合的模。
| 例子 | 计算 |
|---|---|
 |
O i j = 0 6 = 0 O_{ij}=\frac {0} {6}=0 Oij=60=0 |
 |
O i j = 2 6 = 1 3 O_{ij}=\frac {2} {6}=\frac {1} {3} Oij=62=31 |
 |
O i j = 4 6 = 2 3 O_{ij}=\frac {4} {6}=\frac {2} {3} Oij=64=32 |
 |
O i j = 6 6 = 1 O_{ij}=\frac {6} {6}=1 Oij=66=1 |
从社会学的角度来看，这里的Edge overlap，感觉描述的是两个人社交圈子的重合程度。
我们可以从具体的数据中感受一下edge overlap：
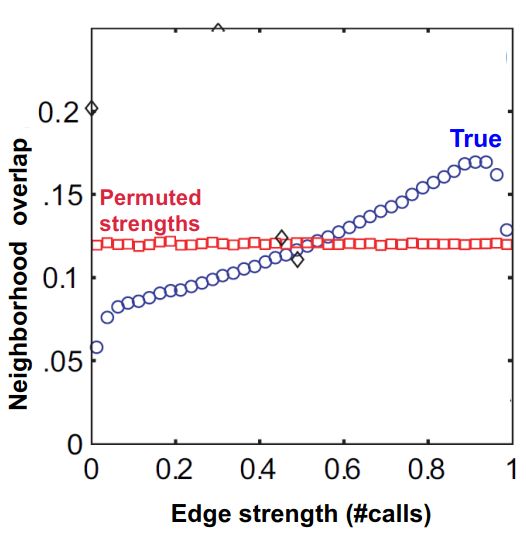
首先，数据来源于cell phone network。这是一张Edge strength（边的强度，代表联系的亲密程度，打电话的次数越多越亲密）和Neignbourhood overlap（邻居重合度）的关系图。蓝色的是真实数据，可以看到联系越紧密的人其实和你的社交圈子的交集就越多。红色的是保持网络结构不变，给网络中的节点随机分配edge strength之后统计的Neignbourhood overlap，会发现社交圈子的重合度与联系的紧密程度无关了，几乎是一条水平直线。
我们再看另一份数据（mobile call graph）：
| 真实数据 | 随机分配edge strength |
|---|---|
 |
 |
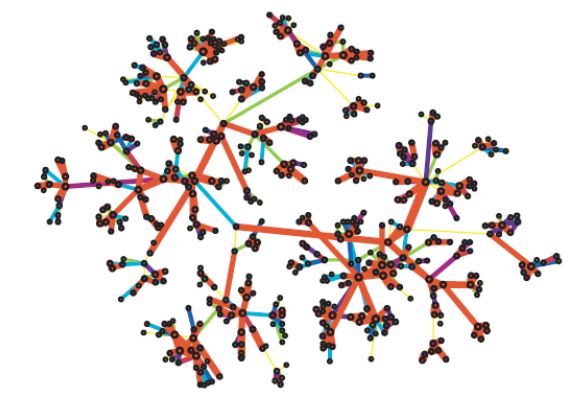可以看到，随机分配edge strength后的网络中，强连接（红色的边）分布得不是那么集中了。
那么我们怎么从这样的一些数据演化成前面提到的概念图呢？我们做下面这样的处理：
| 将网络中的边按照edge strength从低到高删除 | 将网络中的边按照edge overlap从低到高删除 |
|---|---|
 |
 |
可以看到，网络中的最大子图的规模在减小，逐渐形成我们前面提到的概念图：
2. Network communities
根据Granovetter的理论，网络是由紧密相连的节点组成的。
networks are composed of tightly connected sets of nodes.
而Community是具有大量内部连接和很少外部连接(到网络的其余部分)的节点集。
Sets of nodes with lots of internal connections and few external ones (to the rest of the network).
那么，我们怎样去自动检测到网络中的这些节点集（community）呢？
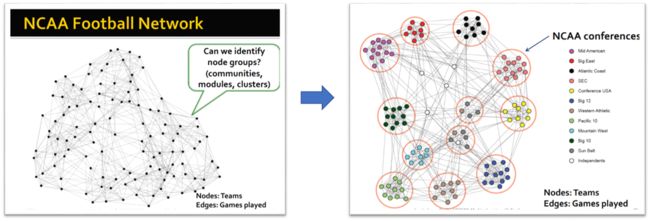
我们首先引入参数 Modularity Q Q Q：
Modularity Q Q Q 衡量的是一个网络社区划分的合理程度。
Modularity Q Q Q：A measure of how well a network is partitioned into communities
划分partition类似于聚类，将节点划分成不同的不相交的子集
假设我们已经有了分组 S S S，那么对于每个组 s s s来说，组内的edges的数量和预期的edges的数量之间的差异，就可以用参数Modularity Q Q Q来衡量。如果这个差值很大，就说明这是一个很凝聚的团体（group）。
那么，我们就需要一个Null Model来得到预期的edges的数量。给定一个包含 n n n个节点、 m m m条边的真实的网络 G G G，重新（随机）地构造新的网络 G ′ G^{'} G′，就得到所需要的Null Model。这个新构造的网络 G ′ G^{'} G′可以看成是一个多重图（multigraph），两个节点之间的预期存在的边可以由下面的公式计算：
这里 k k k为节点的度（如果忘记了可以回顾一下前面课程的内容cs224w 图神经网络 学习笔记（二）Properties of Networks and Random Graph Models）
这样，Modularity Q Q Q就可以由下面这个式子计算：
Q Q Q一般取值在-1到1之间。如果划分的社区内节点之间的连边大于预期，则 Q Q Q为正。通常来说， Q Q Q越大，网络结构的社区划分效果越好，但目前大多数网络在较为合理的社区划分之后，其 Q Q Q值出现在0.3-0.7，在这个区间内的 Q Q Q值意味着网络存在着比较重要的社区结构（significant community structure）。
上面 Q Q Q值计算的公式等价于下面这个式子：
可以发现，计算 Q Q Q值可以衡量目前的社区划分是否合理。但是，我们怎么找到这些社区呢？接下来就要介绍发现社区的算法——Louvain算法。
3. Louvain algorithm——Louvain社区发现算法
Louvain algorithm是一种贪心算法。这部分算法网上有很多资料进行介绍。
参考资料：
社区发现算法-Louvain
Github项目：CommunityDetection
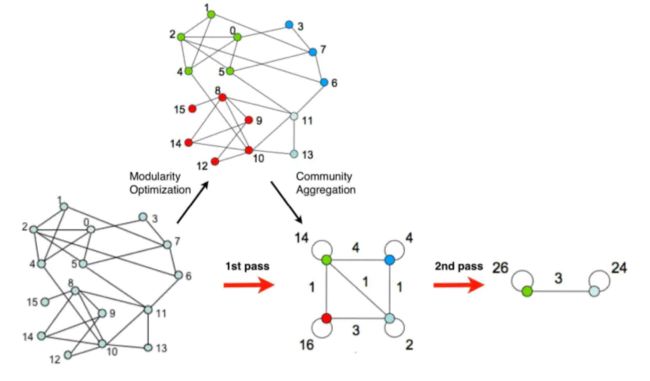
Louvain算法包括两个阶段，在步骤一它不断地遍历网络中的结点，尝试将单个结点加入能够使modularity提升最大的社区中，直到所有结点都不再变化。在步骤二，它处理第一阶段的结果，将一个个小的社区归并为一个超结点来重新构造网络，这时边的权重为两个结点内所有原始结点的边权重之和。迭代这两个步骤直至算法稳定。它的执行流程如图所示：
Louvain算法适用于不重叠的社区发现，但是我们现实生活中很多社区其实是存在重叠的，下面就介绍另一种社区发现算法——BigCLAM。
4. BigCLAM——重叠社区发现算法 Detecting Overlapping Communities
非重叠社区和重叠社区之间的区别还可以从邻接矩阵上看出来：
算法过程共有两步：
第一步：Define a generative model for graphs that is based on node community affiliations. 基于节点社区关系生成一个图，可以采用Community Affiliation Graph Model (AGM)算法，在斯坦福SNAP的官网上可以找到这个算法的简介。
第二步：Given graph , make the assumption that was generated by AGM. Find the best AGM that could have generated . 给定一个真实的图，希望AGM算法生成的图尽可能地贴合真实图。
AGM: Generative process
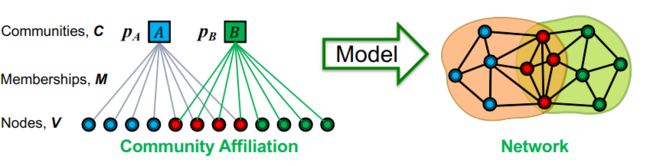
左边是我们预设的社区结构（可以看成一张二分图），我们怎样从这样的社区结构得到一张网络呢？首先，我们给定生成网络的参数：
- Nodes 节点数 V V V
- Communities 社区数 C C C
- Memberships 成员关系 M M M
- 每个社区 c c c都给定一个概率 p c p_c pc， p c p_c pc的含义是社区 c c c内的节点之间生成边的概率。
这样就可以用随机图生成的思想来从预设的社区结构生成网络：
- 当两个节点在同一个社区 c 1 c_1 c1时，节点之间有 p c 1 p_{c1} pc1的概率进行相连。这时
p ( u , v ) = 1 − ∏ c ∈ c 1 ( 1 − p c ) = 1 − 1 + p c 1 = p c 1 p(u,v)=1-\prod_{c \in c_1}(1-p_{c})=1-1+p_{c1}=p_{c1} p(u,v)=1−c∈c1∏(1−pc)=1−1+pc1=pc1 - 当两个节点不属于同一个社区时，节点之间没有边进行相连。这时
p ( u , v ) = 1 − ( 1 − 0 ) = 0 p(u,v)=1-(1-0)=0 p(u,v)=1−(1−0)=0 - 当两个节点属于两个社区（ c 1 c_1 c1和 c 2 c_2 c2）时，
p ( u , v ) = 1 − ∏ c ∈ c 1 ∩ c 2 ( 1 − p c ) = 1 − ( 1 − p c 1 ) ( 1 − p c 2 ) = 1 − ( 1 − p c 1 − p c 1 + p c 1 p c 2 ) = p c 1 + p c 1 − p c 1 p c 2 \begin{aligned} p(u,v) & = 1-\prod_{c \in c_1 \cap c_2}(1-p_{c}) \\ & = 1-(1-p_{c1})(1-p_{c2}) \\ & = 1-(1-p_{c1}-p_{c1}+p_{c1}p_{c2}) \\ & = p_{c1}+p_{c1}-p_{c1}p_{c2} \end{aligned} p(u,v)=1−c∈c1∩c2∏(1−pc)=1−(1−pc1)(1−pc2)=1−(1−pc1−pc1+pc1pc2)=pc1+pc1−pc1pc2
因为 p c 1 p_{c1} pc1和 p c 2 p_{c2} pc2都是小数，所 p ( u , v ) p(u,v) p(u,v)一定大于 p c 1 p_{c1} pc1和 p c 2 p_{c2} pc2。从社交网络上理解，就是两个人所处的共同圈子越多，他们认识的可能性就越大。
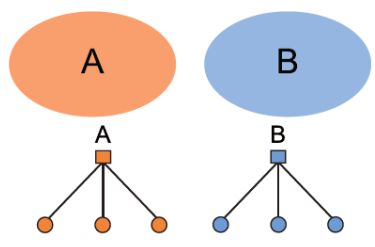
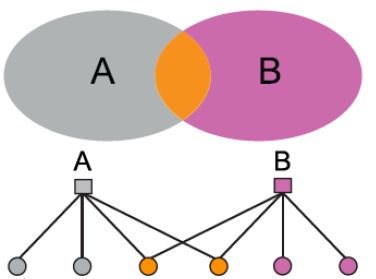
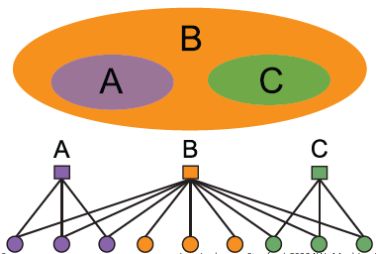
AGM方法的灵活性很高，可以适用于各种网络结构：
| Non-overlapping | Overlapping | Nested |
|---|---|---|
 |
 |
 |
Detecting communities with AGM
上面说的很多内容，是怎么从已知的社区结构得到网络，但是社区发现意味着从已知的网络得到一定的社区结构，也就是前面那个过程的逆过程。也就是说，我们已知网络 G G G，需要找到二分图模型 F F F，且得到相关的参数。
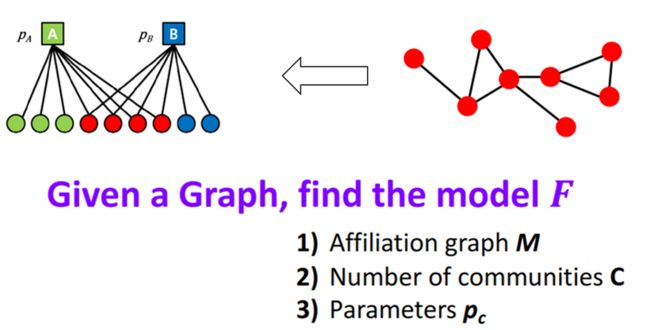
解决这个问题的思路关键在于：已知真实网络 G G G，找到模型 F F F，使得 G G G关于 F F F的条件概率最大（就是上面的正向过程），也就是极大似然估计。
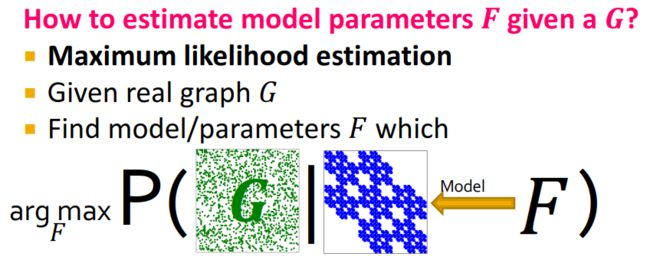
那么，我们就需要找到一个计算条件概率 P ( G ∣ F ) P(G|F) P(G∣F)的高效的方法，并遍历模型 F F F，其中条件概率 P ( G ∣ F ) P(G|F) P(G∣F)最大的模型 F F F就是我们需要的社区结构。
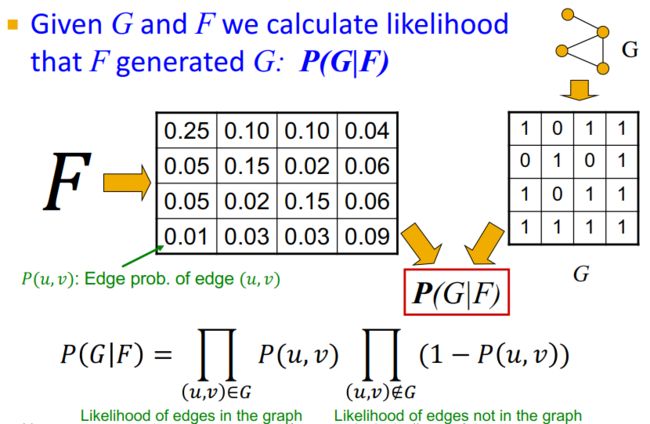
在AGM算法中， p ( u , v ) p(u,v) p(u,v)表示的是两个结点之间产生连边的关系。在真实网络 G G G中，两点相连的时候 p ( u , v ) = 1 p(u,v)=1 p(u,v)=1，两点不相连的时候 p ( u , v ) = 0 p(u,v)=0 p(u,v)=0。在模型 F F F中，为了让它更贴合真实网络 G G G，我们希望相连的两点之间的概率尽可能地大，不相连的两点之间的概率尽可能地小。这样就引入我们的目标函数：
P ( G ∣ F ) = ∏ ( u , v ) ∈ G P ( u , v ) ∏ ( u , v ) ∉ G ( 1 − P ( u , v ) ) P(G|F)=\prod_{(u,v) \in G} P(u,v) \prod_{(u,v) \notin G} (1-P(u,v)) P(G∣F)=(u,v)∈G∏P(u,v)(u,v)∈/G∏(1−P(u,v))
有了目标函数，就可以用梯度下降来求解啦。
BigCLAM的思想是一样的，但是在概率 p ( u , v ) p(u,v) p(u,v)和目标函数的形式上不同：
