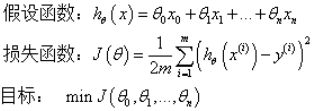分类、回归算法简单介绍
分类
logistic 回归算法
用了一个Logistic Function将线性回归的连续值映射到了{0,1}空间,类似得到事件发生概率值,让自变量的分布和伯努利分布联系起来
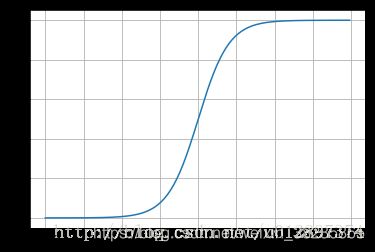
logistic 回归算法使用的是特征的线性组合,最终得到的分隔超平面属于线性模型,只能处理线性可分的二分类问题。
优化Logistic Regression算法的优化有两种:
- 对特征进行处理,如核方法,将线性可分的问题转换为近似线性可分的问题
- 进行扩展,如因子分解机
因子分解机
因子分解机可以处理三类:
- 回归问题
- 二分类问题
- 排序
交叉项系数:
基本线性回归模型基础上引入交叉项,稀疏数据时,观察样本中未出现交互的特征分量时,不能对参数进行估计。
支持向量机
分类预测的确信度
一个样本点距离分隔超平面远近可以表示为分类预测的确信度。
-
函数间隔:分隔超平面关于训练数据集中所有样本点的函数间隔最小值
-
几何间隔:样本到分隔超平面的距离
感知机算法
直接使用分类的样本到分隔超平面之间的距离S作为损失函数,并利用梯度下降法的损失函数的极小值得到最终超平面
问题:超参数的选择产生了不同的分隔超平面
支持向量机
求解出的分隔超平面可以正确划分训练数据集合,而且几何间隔最大。
对于线性可分的二分类问题,在m个训练样本中,与分隔超平面距离最近的样本称为支持向量。在最终的分隔超平面时,只有支持向量起作用,其他样本点不起作用,所以被称为支持向量机。
由于要求所有样本都是线性可分的条件太严苛,所以引入松弛变量。
可以采用核函数的方式将非线性问题转换为线性问题,
回归
线性回归
注意
求解损失函数的最小值有两种方法:梯度下降法以及正规方程
特征缩放:对特征数据进行归一化操作,一是能够提升模型的收敛速度。二是能够提升模型精度
学习率α的选取:如果学习率α选取过小,会导致迭代次数变多,收敛速度变慢;学习率α选取过大,有可能会跳过最优解,最终导致根本无法收敛。
避免过拟合:
(1):丢弃一些对最终预测结果影响不大的特征,PCA算法等;
(2):使用正则化技术,保留所有特征,但是减少特征前面的参数θ的大小,具体就是修改线性回归中的损失函数形式即可,岭回归以及Lasso回归就是这么做的。
普通线性回归算法预测精度不够,如果模型的特征有相关关系,会增加模型复杂度,并且对整个模型的解释能力并没有提高,所以需要对特征进行选择, Ridge回归和Lasso回归都是正则化的特征选择方法。
Ridge回归、Lasso回归
数据集中的特征之间有较强相关时,特征之间出现严重的多重共线性,用普通最小二乘法估计模型参数,参数估计的方差太大,
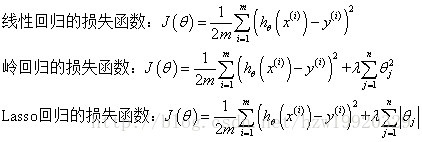


λ称为正则化参数,如果λ选取过大,会把所有参数θ均最小化,造成欠拟合,如果λ选取过小,会导致对过拟合问题解决不当
岭回归与Lasso回归最大的区别
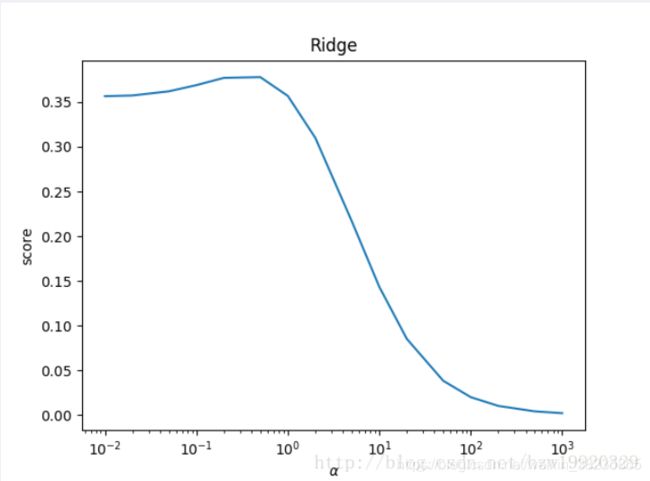
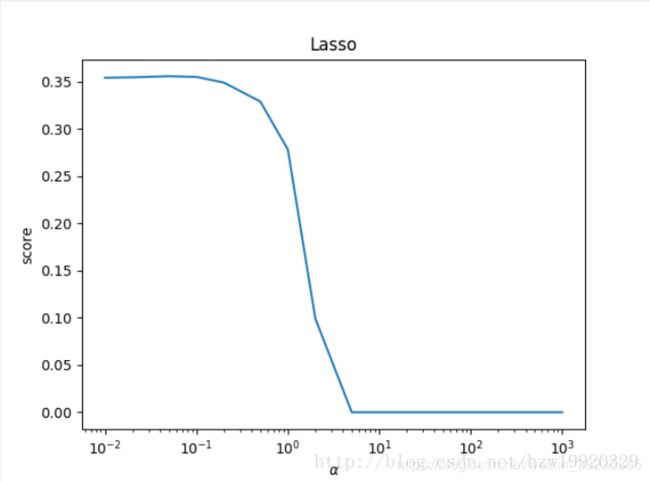
在于岭回归引入的是L2范数惩罚项,Lasso回归引入的是L1范数惩罚项,Lasso回归能够使得损失函数中的许多θ均变成0,这点要优于岭回归,因为岭回归是要所有的θ均存在的,这样计算量Lasso回归将远远小于岭回归。
Lasso回归最终会趋于一条直线,原因就在于好多θ值已经均为0,而岭回归却有一定平滑度,因为所有的θ值均存在
分类:SVM、Logistic回归---->softmax回归
参考:添加链接描述
from sklearn.linear_model import Ridge, Lasso
# ridge 回归模型
rr = Ridge(alpha=0.001)
rr = rr.fit(X_poly, Y_data)
Y_pred_rr = rr.predict(X_poly)
# lasso 回归模型
lassor = Lasso(alpha=0.0001)
lassor = lassor.fit(X_poly, Y_data)
Y_pred_lr = lassor.predict(X_poly)
推荐算法
基于图的推荐算法
PageRank算法时计算图中节点相对于某个节点的重要性算法。
PageRank基于两个假设:
数量假设:一个页面节点接收到其他网页指向的链接数量越多,这个网页就越重要
质量假设:指向页面 入链质量不同,质量高的也页面通过链接像其他页面传递更多的权重
计算过程:
1.有向图转为邻接矩阵
2.计算出链接概率矩阵(对出链进行归一化)
3.计算概率转移矩阵(转置)
4.修改概率转移矩阵(用户有一定概率进入新界面,跳出当前链接的概率为a,a通常取0.85)
5.迭代求解pagerank值(误差在一定范围内停止迭代)
PersonalRank
PageRank算法的变形形式,
用于计算所有商品节点相对于某个用户节点的重要程度。同PageRank算法一样,用户会从用户-商品二部图游走,游走到任一节点会按照一定概率选择停止和继续